【二分查找】
二分查找
- 704. 二分查找
- 35. 搜索插入位置
- 34. 在排序数组中查找元素的第一个和最后一个位置
- 结语
704. 二分查找
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
链接: 二分查找
这个题是一个最基础的二分查找题目,需要你写出二分查找最基础的模板出来。
二分查找有许多的边界问题,每一次边界的处理都要坚持根据区间的定义来操作
,这就是循环不变量规则。
由题可知,该数组是一个升序的有序整型数组,
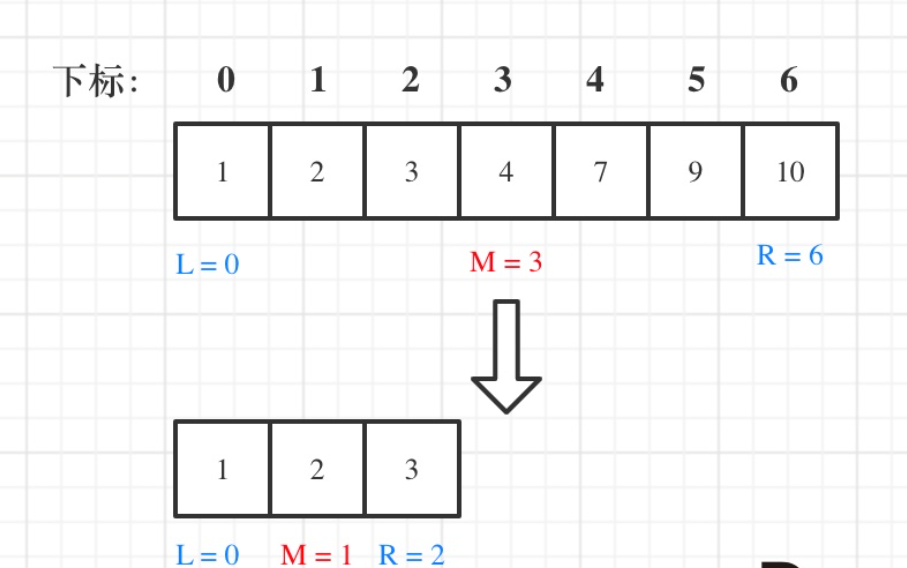
定义一个l变量,一个r变量,一个mid,分别表示的左值,右值,中值。
然后对每一次的mid中值进行一次check,当循环正常结束就是没有target值,
返回-1.
代码:
int search(int* nums, int numsSize, int target){int left=0,right=numsSize-1;int mid=(left+right)/2;while(left<right){if(nums[mid]>=target){right=mid;}else left=mid+1;mid=(left+right)/2;}if(nums[left]==target)return left;return -1;}
35. 搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
输入: nums = [1,3,5,6], target = 5
输出: 2
输入: nums = [1,3,5,6], target = 2
输出: 1
输入: nums = [1,3,5,6], target = 7
输出: 4
链接: 搜索插入位置
这道题是二分查找的稍微进阶,相较于上一题需要考虑边界情况,
以及最后的返回值。
将上一题的代码拷贝下来
while(left<=right)
{if(nums[mid]==target){return mid;}if(nums[mid]>target){right=mid-1;}if(nums[mid]<target){left=mid+1;}mid=(left+right)/2;
这是部分代码,从题中可知,
如果在遍历的时候找到与target对应的值,那么可以直接返回此时的下标mid
如果没有找到的话,循环结束后l,r,mid,这三个下标哪个是正确的返回值呢。
由题意得,返回的是按照值大小顺序插入的位置,所以返回了l的下标。
代码:
int searchInsert(int* nums, int numsSize, int target){int right =numsSize-1;int left=0;int mid=(right+left)/2;while(left<=right){if(nums[mid]==target){return mid;}if(nums[mid]>target){right=mid-1;}if(nums[mid]<target){left=mid+1;}mid=(left+right)/2;}return left;}
34. 在排序数组中查找元素的第一个和最后一个位置
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
示例 3:
输入:nums = [], target = 0
输出:[-1,-1]
链接: 在排序数组中查找元素的第一个和最后一个位置
解题思路:
1.题目要求找出等于target大小的数组元素下标的开始位置和结束位置。
2.也就说需要进行两次二分查找,一次找出开始位置,一次找出结束位置
3.找出开始位置:
- 当数组中有target元素的时候,我们可以将其分为两个部分
- 第一个部分范围为所有 小于target的值
- 第二部分则为所有 大于等于target的值
- 由此可知,第二部分的开头位置的下标即为所求
代码:
int l = 0;int r = nums.size() - 1;int mid = (l + r) / 2;while (l < r){if (nums[mid] >= target){r = mid;}else{l = mid + 1;}mid = (l + r) / 2;}
4.找出结束位置下标:(同上)
- 当数组中有target元素的时候,我们可以将其分为两个部分
- 第一个部分范围为所有 小于等于target的值
- 第二部分则为所有 大于target的值
- 由此可知,第一部分的结束位置的下标即为所求
注意: 此时随着循环更新的是l的值,所以更新方式应改变。mid=(l+r+1)/2
代码:
l = 0;
r = nums.size() - 1;
mid = (l + r+ 1) / 2;
while (l < r)
{if (nums[mid] <= target){l = mid;}else{r = mid - 1;}mid = (r + l+ 1) / 2;
}
每次求出也要检查所求下标对应的值是否为target。
代码:
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {vector<int> ans;//特殊情况处理if(nums.size()==0){ans.push_back(-1);ans.push_back(-1);return ans;}//初始位置int l = 0;int r = nums.size() - 1;int mid = (l + r) / 2;while (l < r){if (nums[mid] >= target){r = mid;}else{l = mid + 1;}mid = (l + r) / 2;}if (nums[l] == target) ans.push_back(l);else ans.push_back(-1);//结束位置l = 0;r = nums.size() - 1;mid = (l + r+ 1) / 2;while (l < r){if (nums[mid] <= target){l = mid;}else{r = mid - 1;}mid = (r + l+ 1) / 2;}if (nums[r] == target) ans.push_back(r);else ans.push_back(-1);return ans;}
};
结语
本期的二分查找到此结束,希望对各位有所帮助
我是Tom-猫
如果觉得有帮助的话,记得
一键三连哦ヾ(≧▽≦*)o。

相关文章:

【二分查找】
二分查找704. 二分查找35. 搜索插入位置34. 在排序数组中查找元素的第一个和最后一个位置结语704. 二分查找 给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在…...
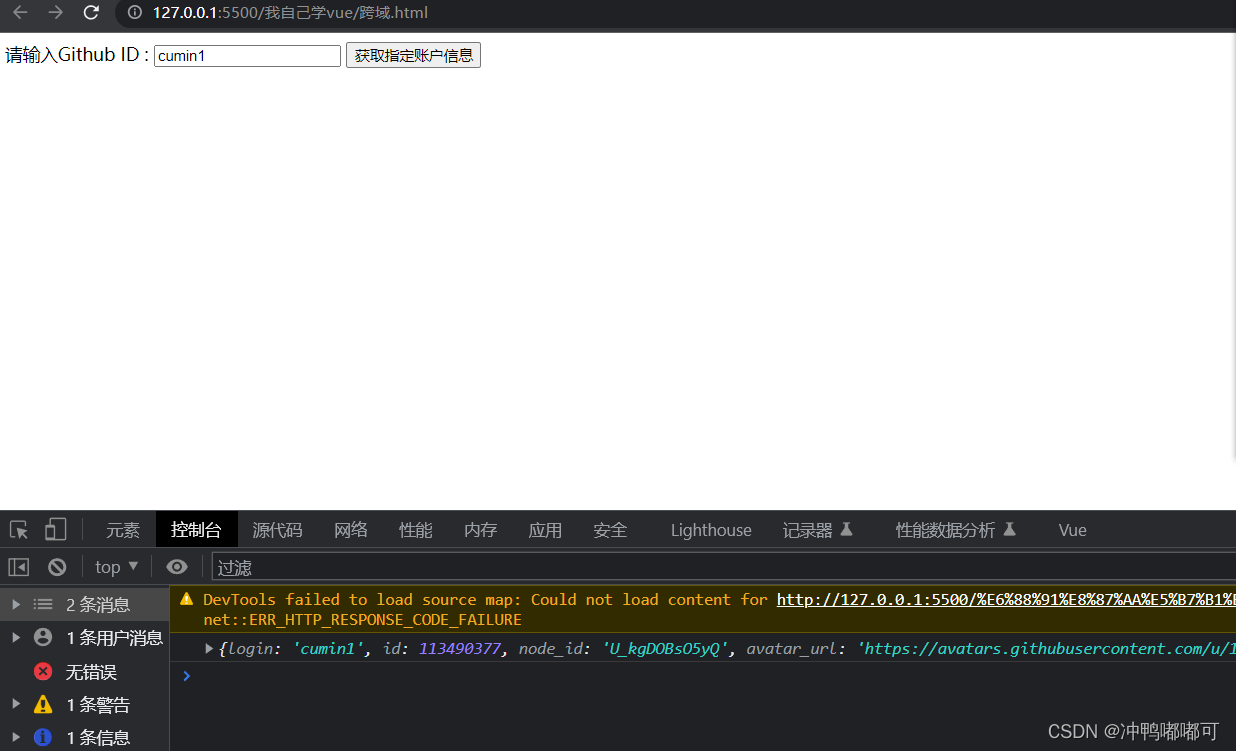
Vue学习 -- 如何用Axios发送请求(get post)Promise对象 跨域请求问题
什么是Axios Vue本身是不支持发送axios请求,需要使用第三方插件,这里推荐使用Axios,Axios是基于promise的HTTP库;它会从浏览器中创建XMLHttpRequset对象。 安装Axios npm install axios -S下载后把axios.js文件复制进项目目录 …...

TVS和稳压管的相同点和不同点
大家好,我是记得诚。 文章目录 介绍相同点不同点介绍 TVS和稳压管都是电路中很常用的电子元器件,都是二极管的一个种类。 TVS二极管全称是Transient voltage suppression diode,也叫瞬态电压抑制二极管。 稳压二极管英文名字Zener diode,又叫齐纳二极管。 关于稳压二极…...

微信小程序项目实例——扫雷
今日推荐💁♂️ 2023许嵩演唱会即将到来🎤🎤🎤大家一起冲冲冲🏃♂️🏃♂️🏃♂️ 🔮🔮🔮🔮🔮往期优质项目实例🔮…...
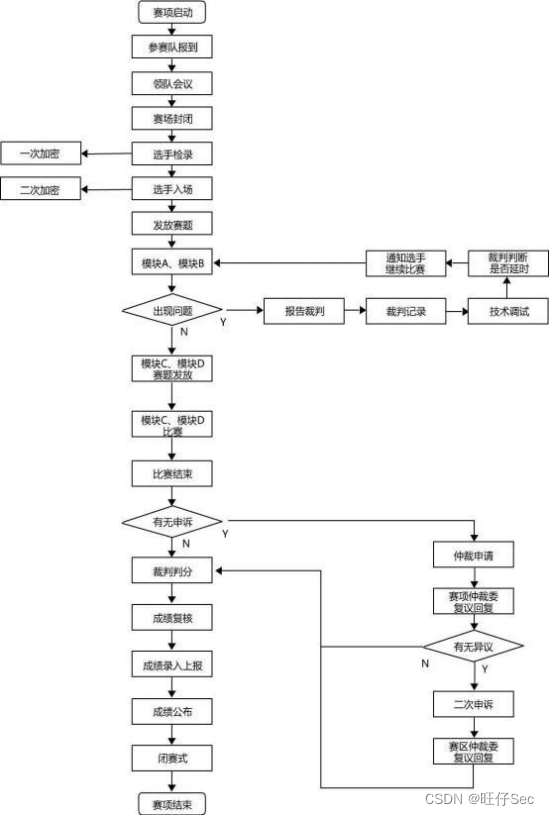
2022-2023年度广东省职业院校学生专业技能大赛 中职组网络安全赛项竞赛规程
2022-2023年度广东省职业院校学生专业技能大赛 中职组网络安全赛项竞赛规程 一、赛项名称 赛项编号:Z27 赛项名称:网络安全赛项组别:中职 赛项归属:信息技术类 二、竞赛目的 为检验中职学校网络信息安全人才培养成效,促…...
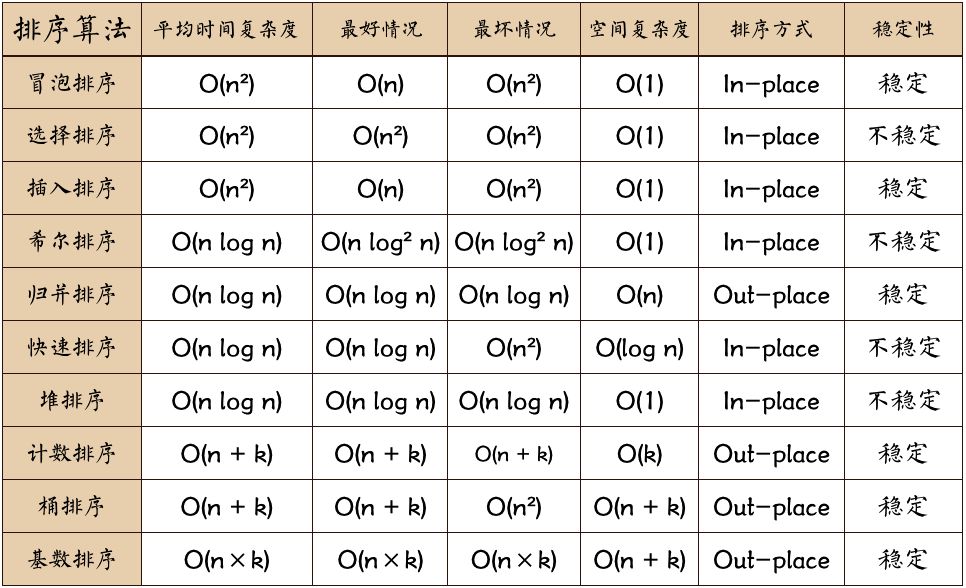
超详细的堆排序,进来看看吧。
1.堆的基本概念1.1什么是堆堆是一种叫做完全二叉树的数据结构,1.2大堆和小堆大堆:每个节点的值都大于或者等于他的左右孩子节点的值小根堆:每个结点的值都小于或等于其左孩子和右孩子结点的值1.3完全二叉树节点之间的关系leftchild parent*2 1rightchild parent*…...
线性回归 特征扩展的原理与python代码的实现
文章目录1 多项式扩展的作用2 多项式扩展的函数2.1 接收参数2.2 多项式扩展示例3 多项式扩展的完整实例1 多项式扩展的作用 在线性回归中,多项式扩展是种比较常见的技术,可以通过增加特征的数量和多项式项的次数来提高模型的拟合能力。 举个例子&#…...

订阅关系一致
订阅关系一致指的是同一个消费者Group ID下所有Consumer实例所订阅的Topic、Tag必须完全一致。如果订阅关系不一致,消息消费的逻辑就会混乱,甚至导致消息丢失。本文提供订阅关系一致的正确示例代码以及订阅关系不一致的可能原因,帮助您顺畅地订阅消息。 背景信息 消息队列Ro…...

测试老鸟都在用的接口抓包常用工具以及接口测试工具都有哪些?
目录 接口 接口测试的重要性 常用抓包工具 常用接口测试工具 接口 接口测试是测试系统组件间接口的一种测试。接口测试主要用于检测外部系统与系统之间以及内部各个子系统之间的交互点。测试的重点是要检查数据的交换,传递和控制管理过程,以及系统间…...
Delphi 一个函数实现腾讯云最新版(API3.0)短信发送
目录 一、腾讯云短信基本知识 1. 需要在腾讯云后台注册账号 2. 需要在腾讯云中开通短信功能 3. 腾讯云短信版本说明 4. 短信内容的组成 特定规范 二、短信发送函数 三、下载源代码(收费) 一、腾讯云短信基本知识 如今我们随时都收到短信验证码,注册码等等。这是…...

2023年Android现代开发
2023年现代Android开发 下面与大家分享如何构建具有2023年最新趋势的Android应用程序。 Android是什么? Android 是一种基于 Linux 内核并由 Google 开发的开源操作系统。它用于各种设备,包括智能手机、平板电脑、电视和智能手表。 目前,…...

自然语言处理(NLP)在医疗领域的应用
自然语言处理(Natural Language Processing,NLP)是计算机科学领域与人工智能领域中的一个重要方向。它研究能实现人与计算机之间用自然语言进行有效通信的各种理论和方法。在各个领域都有其应用。 其在生物医学领域迅速发展,已经…...

计算机中的浮点数运算
计算机中的浮点数 计算机中以固定长度存储浮点数的方式,造成了浮点数运算过程容易产生上溢和下溢。以float32为例, 其标记位占1bit,指数位占8bit,小数部分占23bit 经典下溢场景 不满足精度导致截断误差 #include <iostream> #include <iomanip> usin…...

看了字节跳动月薪20K+测试岗面试题,让我这个工作3年的测试工程师,冷汗直流....
朋友入职已经两周了,整体工作环境还是非常满意的!所以这次特意抽空给我写出了这份面试题,而我把它分享给伙伴们,面试&入职的经验! 大概是在2月中的时候他告诉我投递了字节跳动并且简历已通过,2月23经过…...
这两天最好的ChatGPT应用;使用Notion AI提升效率的经验(13);AI编程与程序员的生存 | ShowMeAI日报
👀日报合辑 | 🎡生产力工具与行业应用大全 | 🧡 点赞关注评论拜托啦! 🤖 硅谷银行风波中,OpenAI 创始人大方帮助硅谷初创公司:钱先拿着用,有了再还 OpenAI 创始人 Sam Altman 的弟弟…...

Linux 内核likely与unlikey
内核源码的时候经常可以看到likely()和unlikely()函数,这两个函数的作用是什么?-- 先得学一学GCC提供的内建函数!! likely和unlikely内核中的定义 # define likely(x) __builtin_expect(!!(x), 1) # define unlikely(x) __built…...

成功解决主从同步异常之Slave_IO_Running显示为No的问题
前言 MySQL主从同步在做的过程中很容易出问题, 尤其是双主配置,参数多,需要在两台服务器中反复操作,容易搞错导致失败,这里汇总的是主从同步异常之Slave_IO_Running显示为No的解决方案。 文章目录 前言一. 问题重现二. 排查过程2.1 查看UUID是否相同,并修改2.2 修改完UU…...

面试阿里测开岗失败后,被面试官在朋友圈吐槽了......
前一阵子有个徒弟向我诉苦,说自己在参加某大厂测试面试的时候被面试官怼得哑口无言,场面让他一度十分尴尬印象最深的就是下面几个问题:根据你以前的工作经验和学习到的测试技术,说说你对质量保证的理解?非关系型数据库…...

蓝桥杯嵌入式--字符串比较在串口通信中的应用
前言今天做了个模拟题,大致意思是接收上位机发的字符串,然后执行相应操作。思路很明确,就是把接收到的内容进行比较,但是从前我只学过比较数字的方式,即直接用“”进行比较,但是字符串不能使用这个方法&…...
考研408每周一题(2019 41)
2019年(单链表) 41.(13分)设线性表L(a1,a2,a3,...,a(n-2),a(n-1),an)采用带头结点的单链表保存,链表中的结点定义如下: typedef struct node {int data;struct node *next; } NODE; 请设计一个空间复杂度为O(1)且时间上尽可能高效的算法&…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...
