【数据结构】链式二叉树的实现和思路分析及二叉树OJ
【数据结构】链式二叉树的实现和思路分析及二叉树OJ

🔥个人主页:大白的编程日记
🔥专栏:数据结构
文章目录
- 【数据结构】链式二叉树的实现和思路分析及二叉树OJ
- 前言
- 一.链式二叉树的定义及结构
- 二.链式二叉树的遍历
- 2.1前序遍历
- 2.2中序遍历
- 2.3后序遍历
- 2.4层序遍历
- 三.链式二叉树功能函数
- 3.1节点个数
- 3.2第k层节点的个数
- 3.3查找值为x的节点
- 3.4树的销毁
- 四.二叉树OJ
- 4.1二叉树遍历
- 4.2左子叶之和
- 后言
前言
哈喽,各位小伙伴大家好!上期讲的是用顺序表实现二叉树。今天咱们用链表的方式实现我们的二叉树。也就是链式结构。话不多说,咱们进入正题!向大厂冲锋!
一.链式二叉树的定义及结构
- 树的定义
我们链式二叉树用结构体定义。结构体内包含节点的数据。然后还有指向左右孩子节点的结构体指针
typedef int DataType;
typedef struct BinaryTreeNode
{DataType val;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
- 节点的创建
节点的创建我们需要malloc一个结构体。检查节点是否开辟成功。然后将节点数据赋值为X即可。再将左右指针指向空。最后返回开辟好的节点。
BTNode* BuyNode(int x)//创建树的节点
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");exit(1);}node->a = x;node->left = node->right = NULL;return node;
}
- 树的创建
为了方便我们后面使用。我们先开辟一个树出来。
我们只需要创建好节点。然后修改节点的指针使其成一棵树即可。

BTNode* CreatTree()//建树
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}
这样一颗树二叉树就构建好了。
二.链式二叉树的遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉
树中的结点进行相应的操作,并且每个结点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历
是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
- 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
- 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
- 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为
根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。

任何一颗树都要分成根 左子树 右子树去按顺序遍历。
左右子树的访问又看成一颗树继续按照顺序去遍历。
2.1前序遍历
前序遍历访问顺序就是 根 左子树 右子树。
然后子树继续按照 根 左子树 右子树访问。
那我们先把一棵树的按照根 左子树 右子树拆分

- 代码实现
我们前序遍历一颗树时分为两种情况
一:树为空。那就不用访问了直接return结束。
二:树不为空。那就先访问根节点(这里我们直接打印)。然后还需要继续左右子树前序遍历,那我们就递归函数解决。
void PrevOrder(BTNode* p)//前序遍历
{if (p == NULL){printf("N ");return;}printf("%d ", p->a);PrevOrder(p->left);PrevOrder(p->right);
}
- 逻辑分析
逻辑上我们就是将一颗树的前序遍历分为根的访问和左子树的遍历和右子树。
左右子树的遍历又看成一棵树的前序遍历。所以我们递归左右子树即可。



- 逻辑过程
我们都知道函数的调用需要在栈上开辟栈帧。
但是需要注意的是左子树开辟的栈帧函数调用结束销毁后
仍然存在内存中,调用右子树开辟的栈帧是重复利用左子树的栈帧。
所以函数的栈帧会重复利用。

2.2中序遍历
以此类推,中序就先递归左子树 再访问根 再递归右子树即可。
void InorOrder(BTNode* p)//中序遍历
{if (p == NULL){printf("N ");return;}InorOrder(p->left);printf("%d ", p->a);InorOrder(p->right);
}
2.3后序遍历
以此类推,中序就先访问根 递归左子树 再递归右子树即可。
void PostOrder(BTNode* p)//后序遍历
{if (p == NULL){printf("N ");return;}PostOrder(p->left);PostOrder(p->right);printf("%d ", p->a);
}
- 验证

2.4层序遍历
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根结点所在层数为1,层序遍历就是从所在二叉树的根结点出发,首先访问第一层的树根结点,然后从左到右访问第2层上的结点,接着是第三层的结点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。

- 思路分析

上一层带下一层即可完成层序遍历。
- 代码实现
void TreeLevelOrder(BTNode* p)//层序遍历
{Queue pq;QueueInit(&pq);//初始化队列if(p)QueuePush(&pq, p);//第一层入队列while (!QueueEmpty(&pq))//队列不为空{BTNode* head = QueueFron(&pq);//取出队头数据QueuePop(&pq);//出队列printf("%d ", head->a);//访问if (head->left){QueuePush(&pq, head->left);//左孩子入队列}if (head->right){QueuePush(&pq, head->right);//右孩子入队列}}QueueDestroy(&pq);//销毁队列
}
三.链式二叉树功能函数
我们链式二叉树的实现不只是实现遍历而已。
我们还需要对二叉树实现求节点个数,树的高度等等。
3.1节点个数

- 遍历计数
我们很容易想到走一个遍历然后不为空用size++记录个数即可。
这确实是一种方法。那具体代码如何实现呢?
int TreeSize(BTNode* p)//树的节点个数
{int size;if (p == NULL){return 0;}size++;TreeSize(p->left);TreeSize(p->right);return size;
}
这样写对吗?不对因为size是局部变量。每次函数调用size都会置为0.
这样就不能把节点个数累加起来。size之会累加第一次。

那我们是不是把他static改成静态让他的生命周期是全局的
这样每次size++都是同一个size就可以了呢?
int TreeSize(BTNode* p)//树的节点个数
{static int size=0;if (p == NULL){return 0;}size++;TreeSize(p->left);TreeSize(p->right);return size;
}

我们发现结果确实是6。那我在调用一次呢?

我们发现第二次调用是12。为什么呢?因为局部静态变量只会初始化一次。
所以第二次调用6+6就是12.
int size;
int TreeSize(BTNode* p)//树的节点个数
{if (p == NULL){return 0;}size++;TreeSize(p->left);TreeSize(p->right);return size;
}
那我们只能用全局的size然后每次函数调用前都要手动置0.

- 分治递归
我们可以用递归的思想把大问题拆分成小问题解决。

int TreeSize(BTNode* p)//树的节点个数
{if (p == NULL){return 0;}return TreeSize(p->left)+TreeSize(p->right)+1;
}

3.2第k层节点的个数
现在我们要求树的第k层节点的个数。我们该怎么求呢?
还是用递归的思想。

把问题转化为下一层第k-1层的递归求解即可。
int TreeLevelKSize(BTNode* p, int k)//第k层的节点
{if (p == NULL){return 0;}if (k == 1){return 1;}return TreeLevelKSize(p->left, k - 1)+TreeLevelKSize(p->right, k - 1);
}

3.3查找值为x的节点
现在我们要查找值为x的节点。一棵树可能有多个节点值为x。我们就返回找到的第一个节点即可。

利用递归分治的思想。将一棵树x节点的查找分为根节点 左子树 右子树的查找即可。
- 代码实现
BTNode* TreeFind(BTNode* p, int x)//查找值为k的节点
{if (p == NULL){return NULL;}if (p->a == x){return p;}BTNode* ret1 = TreeFind(p->left, x);BTNode* ret2 = TreeFind(p->right, x);return ret1 == NULL ? ret2 : ret1;
}
我们这样写对吗?
其实也算对。但是这样有小问题就是不管左子树存不存在x节点。都会去再查找右子树。这样就效率不太高。
BTNode* TreeFind(BTNode* p, int x)//查找值为k的节点
{if (p == NULL){return NULL;}if (p->a == x){return p;}BTNode* ret1 = TreeFind(p->left, x);if (ret1 != NULL){return ret1;}BTNode* ret2 = TreeFind(p->right, x);if (ret2 != NULL){return ret2;}return NULL;
}
所以我们最好对左子树的返回值检查一下。
如果不为空说明找到。直接return返回节点即可。
3.4树的销毁
那树如何销毁呢?

把树的销毁看成根的销毁 左右子树的销毁。
左右子树又是树的销毁 递归即可。
void TreeDestroy(BTNode* p)//树的销毁
{if (p == NULL){return ;}TreeDestroy(p->left);//销毁左子树TreeDestroy(p->right);//销毁右子树free(p);//销毁根节点
}
- 判断完全二叉树
现在我们要判断一棵树是否时完全二叉树如何判断呢?

我们只需要走一个层序遍历。然后出队列时孩子节点入队列即可。 - 代码实现
bool FullTree(BTNode* p)//判断是否满二叉树
{Queue pq;QueueInit(&pq);if (p)QueuePush(&pq, p);while (!QueueEmpty(&pq))//入队列{BTNode* head = QueueFron(&pq);QueuePop(&pq);//出队列if (head == NULL){break;}QueuePush(&pq, head->left);//左孩子入队列QueuePush(&pq, head->right);//右孩子入队列}while (!QueueEmpty(&pq)){BTNode* head = QueueFron(&pq);QueuePop(&pq);if (head)//找是否有非空节点{QueueDestroy(&pq);return false;}}QueueDestroy(&pq);return true;
}
四.二叉树OJ
4.1二叉树遍历
- 题目
二叉树遍历

- 思路分析

这里我们还是用递归的方式。
根据前序遍历的思想构建树。然后走中序遍历即可。
- 代码实现
#include <stdio.h>
typedef char DataType;
typedef struct BinaryTreeNode {DataType a;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
} BTNode;
void InorOrder(BTNode* p)//中序遍历
{if (p == NULL){return;}InorOrder(p->left);printf("%c ", p->a);InorOrder(p->right);
}
BTNode* CreatTree(char* p, int* i) //构建树
{ //前序遍历if (p[*i] == '#')//不为空{(*i)++;return NULL;}BTNode* ret = (BTNode*)malloc(sizeof(BTNode));//创建一个节点if (ret == NULL){perror("malloc fali");exit(1);}ret->a = p[(*i)++];//赋值ret->left = CreatTree(p, i);//左节点ret->right = CreatTree(p, i);//右节点return ret;//返回节点}
int main() {char s[100];scanf("%s", &s);int i = 0;BTNode* ret = CreatTree(s, &i);//构建二叉树InorOrder(ret);//中序遍历return 0;
}
4.2左子叶之和
- 题目
左子叶之和

-
思路分析

这里我们还是用递归的思想将树的左子叶之和分为
左子树左子叶+右子树左子叶之和即可。 -
代码实现
int sumOfLeftLeaves(struct TreeNode* root){if(root==NULL){return 0;}if(root->left&&(root->left->left==NULL&&root->left->right==NULL)){return root->right==NULL?root->left->val:sumOfLeftLeaves(root->right)+root->left->val;}return sumOfLeftLeaves(root->left)+sumOfLeftLeaves(root->right);
}
后言
这就是链式二叉树的实现以及二叉树OJ。这是数据结构中比较难也是重点内容。
大家一定要好好消化。今天就分享到这。感谢各位的耐心垂阅!咱们下期见!拜拜~

相关文章:

【数据结构】链式二叉树的实现和思路分析及二叉树OJ
【数据结构】链式二叉树的实现和思路分析及二叉树OJ 🔥个人主页:大白的编程日记 🔥专栏:数据结构 文章目录 【数据结构】链式二叉树的实现和思路分析及二叉树OJ前言一.链式二叉树的定义及结构二.链式二叉树的遍历2.1前序遍历2.2中…...
项目成功秘诀:工单管理系统如何加速进程
国内外主流的10款项目工单管理系统对比:PingCode、Worktile、浪潮云工单管理系统、华为企业智能工单系统、金蝶云苍穹、紫光软件管理系统、Jira、Asana、ServiceNow、Smartsheet。 在管理日益复杂的个人项目时,找到一款能够真正符合需求的管理软件&#…...

OpenGauss和GaussDB有何不同
OpenGauss和GaussDB是两个不同的数据库产品,它们都具有高性能、高可靠性和高可扩展性等优点,但是它们之间也有一些区别和相似之处。了解它们之间的关系、区别、建议、适用场景和如何学习,对于提高技能和保持行业敏感性非常重要。本文将深入探…...
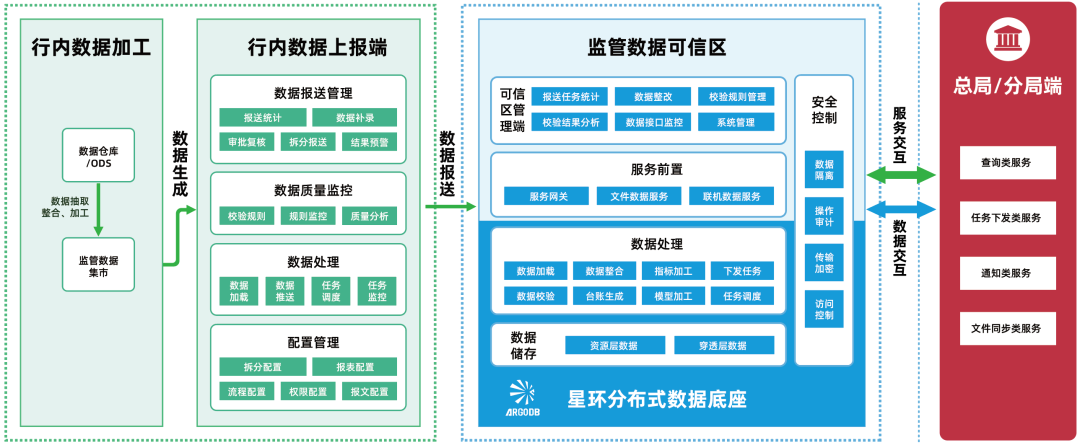
星环科技携手东华软件推出一表通报送联合解决方案
随着国家金融监督管理总局“一表通”试点工作的持续推进,星环科技携手东华软件推出了基于星环科技分布式分析型数据库ArgoDB和大数据基础平台TDH的一表通报送联合解决方案,并已在多地实施落地中得到充分验证。 星环科技与东华软件作为战略合作伙伴&…...

YOLOv10环境搭建、训练自己的目标检测数据集、实际验证和测试
1 环境搭建 1.1 在官方仓库的给定的使用python3.9版本,则使用conda创建对应虚拟环境。 conda create -n yolov10 python3.9 1.2 切换到对应虚拟环境 conda activate yolov10 1.3 在指定目录下克隆yolov10官方仓库代码 git clone https://github.com/THU-MIG/yo…...

Harmony Next -- 通用标题栏:高度自定义,可设置沉浸式状态,正常状态下为:左侧返回、居中标题,左中右均可自定义视图。
hm_common_title_bar OpenHarmony三方库中心仓:https://ohpm.openharmony.cn/#/cn/detail/common_title_bar 介绍 一款通用标题栏,支持高度自定义,可设置沉浸式状态,正常状态下为:左侧返回、居中标题,左…...

甄选范文“论数据分片技术及其应用”软考高级论文,系统架构设计师论文
论文真题 数据分片就是按照一定的规则,将数据集划分成相互独立、正交的数据子集,然后将数据子集分布到不同的节点上。通过设计合理的数据分片规则,可将系统中的数据分布在不同的物理数据库中,达到提升应用系统数据处理速度的目的。 请围绕“论数据分片技术及其应用”论题…...

【elementui】记录el-table设置左、右列固定时,加大滚动条宽度至使滚动条部分被固定列遮挡的解决方法
当前elementui版本:2.8.2 现象:此处el-table__body-wrapper默认的滚动条宽度为8px,我加大到10px,如果不设置fixed一切正常,设置fixed后会被遮挡一点 el-table__fixed-right::before, .el-table__fixed::before 设置…...

Python人工智能:一、语音合成和语音识别
在Python中,语音合成(Text-To-Speech, TTS)和语音识别(Speech-To-Text, STT)是两个非常重要的功能,它们在人工智能、自动化、辅助技术以及许多其他领域都有广泛的应用。下面将分别介绍这两个领域在Python中…...

C/C++进阶 (8)哈希表(STL)
个人主页:仍有未知等待探索-CSDN博客 专题分栏:C 本文着重于模拟实现哈希表,并非是哈希表的使用。 实现的哈希表的底层用的是线性探测法,并非是哈希桶。 目录 一、标准库中的哈希表 1、unordered_map 2、unordered_set 二、模…...
2024电赛H题参考方案(+视频演示+核心控制代码)——自动行驶小车
目录 一、题目要求 二、参考资源获取 三、TI板子可能用到的资源 1、环境搭建及工程移植 2、相关模块的移植 四、控制参考方案 1、整体控制方案视频演示 2、视频演示部分核心代码 五、总结 一、题目要求 小编自认为:此次控制类类型题目的H题,相较于往年较…...

设计模式14-享元模式
设计模式14-享元模式 由来动机定义与结构代码推导特点享元模式的应用总结优点缺点使用享元模式的注意事项 由来动机 在很多应用中,可能会创建大量相似对象,例如在文字处理器中每个字符对象。在这些场景下,如果每个对象都独立存在,…...

Javascript中canvas与svg详解
Canvas 在JavaScript中,<canvas> 元素用于在网页上绘制图形,如线条、圆形、矩形、图像等。它是一个通过JavaScript和HTML的<canvas>元素来工作的绘图表面。<canvas> 元素自身并不具备绘图能力,它仅仅提供了一个绘图环境&a…...

【BUG】已解决:No Python at ‘C:Users…Python Python39python. exe’
No Python at ‘C:Users…Python Python39python. exe’ 目录 No Python at ‘C:Users…Python Python39python. exe’ 【常见模块错误】 【解决方案】 欢迎来到英杰社区https://bbs.csdn.net/topics/617804998 欢迎来到我的主页,我是博主英杰,211科班…...

Flink SQL 的工作机制
前言 Flink SQL 引擎的工作流总结如图所示。 从图中可以看出,一段查询 SQL / 使用TableAPI 编写的程序(以下简称 TableAPI 代码)从输入到编译为可执行的 JobGraph 主要经历如下几个阶段: 将 SQL文本 / TableAPI 代码转化为逻辑执…...

[AI Mem0] 源码解读,带你了解 Mem0 的实现
Mem0 的 CRUD 到底是如何实现的?我们来看下源码。 使用 先来看下,如何使用 Mem0 import os os.environ["OPENAI_API_KEY"] "sk-xxx"from mem0 import Memorym Memory()# 1. Add: Store a memory from any unstructured text re…...

【LLM】-10-部署llama-3-chinese-8b-instruct-v3 大模型
目录 1、模型下载 2、下载项目代码 3、启动模型 4、模型调用 4.1、completion接口 4.2、聊天(chat completion) 4.3、多轮对话 4.4、文本嵌入向量 5、Java代码实现调用 由于在【LLM】-09-搭建问答系统-对输入Prompt检查-CSDN博客 关于提示词注入…...

C语言 之 理解指针(4)
文章目录 1. 字符指针变量2. 数组指针变量2.1 对数组指针变量的理解2.2 数组指针变量的初始化 3. 二维数组传参的本质4. 函数指针变量4.1 函数指针变量的创建4.2 函数指针变量的使用 5. 函数指针数组 1. 字符指针变量 我们在前面使用的主要是整形指针变量,现在要学…...

Java设计模式—单例模式(Singleton Pattern)
目录 一、定义 二、应用场景 三、具体实现 示例一 示例二 四、懒汉与饿汉 饿汉模式 懒汉模式 五、总结 六、说明 一、定义 二、应用场景 单例模式的应用场景主要包括以下几个方面: 日志系统:在应用程序中,通常只需要一个日…...

AV1帧间预测(二):运动补偿
运动补偿(Motion Compensation,MC)是帧间预测最基础的工具,AV1支持两种运动补偿方式,一种是传统的平移运动补偿,另一种是仿射运动补偿。下面分别介绍这两种运动补偿方法。 平移运动补偿 平移运动补偿是最传统的运动补偿方式,H.26…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

Django RBAC项目后端实战 - 03 DRF权限控制实现
项目背景 在上一篇文章中,我们完成了JWT认证系统的集成。本篇文章将实现基于Redis的RBAC权限控制系统,为系统提供细粒度的权限控制。 开发目标 实现基于Redis的权限缓存机制开发DRF权限控制类实现权限管理API配置权限白名单 前置配置 在开始开发权限…...

虚幻基础:角色旋转
能帮到你的话,就给个赞吧 😘 文章目录 移动组件使用控制器所需旋转:组件 使用 控制器旋转将旋转朝向运动:组件 使用 移动方向旋转 控制器旋转和移动旋转 缺点移动旋转:必须移动才能旋转,不移动不旋转控制器…...

