【C++高阶数据结构】红黑树:全面剖析与深度学习
目录
- 🚀 前言:红黑树与AVL树的比较
- 一: 🔥 红黑树的概念
- 二: 🔥 红黑树的性质
- 三: 🔥 红黑树节点的定义和结构
- 🚀 3.1 基本元素
- 🚀 3.2 节点颜色
- 🚀 3.3 构造函数
- 🚀 3.4 红黑树节点的定义
- 四:🔥 红黑树的插入操作
- 五:🔥 红黑树的验证
- 六:🔥 红黑树的完整代码

🚀 前言:红黑树与AVL树的比较
红黑树和AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是O( l o g 2 N log_2 N log2N),红黑树不追
求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对而言,降低了插入和旋转的次数,
所以在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单,所以实际运用中红
黑树更多。
一: 🔥 红黑树的概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。

二: 🔥 红黑树的性质
1. 每个结点不是红色就是黑色
2. 根节点是黑色的
3. 如果一个节点是红色的,则它的两个孩子结点是黑色的
4. 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点
5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
思考:为什么满足上面的性质,红黑树就能保证:其最长路径中节点个数不会超过最短路径节点个数的两倍?
三: 🔥 红黑树节点的定义和结构
🚀 3.1 基本元素
_left:指向节点的左子节点的指针_right:指向节点的右子节点的指针_parent:指向节点的父节点的指针_kv:一个结构体或配对(pair),包含节点的键值(key)和值(value)。这取决于红黑的具体用途,可能只包含键或包含键值对。_col:表示当前节点的颜色。
🚀 3.2 节点颜色
在上面的定义中,_col 成员变量用于表示节点的颜色,通过 Color 枚举类型来定义,可以是 RED 或 BLACK。
🚀 3.3 构造函数
初始化一个新节点时,通常需要一个构造函数,它接受一个键值对(或仅键),并设置节点的左子节点、右子节点、父节点和颜色(初始化为红色)
🚀 3.4 红黑树节点的定义
// 节点的颜色
enum Color{RED, BLACK};
// 红黑树节点的定义
template<class ValueType>
struct RBTreeNode
{RBTreeNode(const ValueType& data = ValueType(),Color color = RED): _pLeft(nullptr), _pRight(nullptr), _pParent(nullptr), _data(data), _color(color){}RBTreeNode<ValueType>* _pLeft; // 节点的左孩子RBTreeNode<ValueType>* _pRight; // 节点的右孩子RBTreeNode<ValueType>* _pParent; // 节点的双亲(红黑树需要旋转,为了实现简单给出该字段)ValueType _data; // 节点的值域Color _color; // 节点的颜色
}
思考:在节点的定义中,为什么要将节点的默认颜色给成红色的?
答案:优先增加黑色节点会破坏红黑树的默认规则和结构,而新插入红色节点可以通过调整来适应规则,不一定会破坏结构。
四:🔥 红黑树的插入操作
- 红黑树是在二叉搜索树的基础上加上其平衡限制条件,因此红黑树的插入可分为两步:
1. 按照二叉搜索的树规则插入新节点
template<class ValueType>
class RBTree
{//……bool Insert(const ValueType& data){PNode& pRoot = GetRoot();if (nullptr == pRoot){pRoot = new Node(data, BLACK);// 根的双亲为头节点pRoot->_pParent = _pHead;_pHead->_pParent = pRoot;}else{// 1. 按照二叉搜索的树方式插入新节点// 2. 检测新节点插入后,红黑树的性质是否造到破坏,// 若满足直接退出,否则对红黑树进行旋转着色处理}// 根节点的颜色可能被修改,将其改回黑色pRoot->_color = BLACK;_pHead->_pLeft = LeftMost();_pHead->_pRight = RightMost();return true;}
private:PNode& GetRoot(){ return _pHead->_pParent;}// 获取红黑树中最小节点,即最左侧节点PNode LeftMost();// 获取红黑树中最大节点,即最右侧节点PNode RightMost();
private:PNode _pHead;
};
2. 检测新节点插入后,红黑树的性质是否造到破坏
因为新节点的默认颜色是红色,因此:如果其双亲节点的颜色是黑色,没有违反红黑树任何
性质,则不需要调整;但当新插入节点的双亲节点颜色为红色时,就违反了性质三不能有连
在一起的红色节点,此时需要对红黑树分情况来讨论:
约定 : cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点
- 情况一: cur为红,p为红,g为黑,u存在且为红

cur和p均为红,违反了性质三,此处能否将p直接改为黑?
解决方式:将p,u改为黑,g改为红,然后把g当成cur,继续向上调整。
-
情况二 : cur为红,p为红,g为黑,u不存在/u存在且为黑

p为g的左孩子,cur为p的左孩子,则进行右单旋转;相反,
p为g的右孩子,cur为p的右孩子,则进行左单旋转
p、g变色–p变黑,g变红 -
情况三 : cur为红,p为红,g为黑,u不存在 / u存在且为黑

解决方式: p为g的左孩子,cur为p的右孩子,则针对p做左单旋转;相反,p为g的右孩子,cur为p的左孩子,则针对p做右单旋转则转换成了情况2
具体实现代码如下:
bool Insert(const pair<K, V>& kv){if (_root == nullptr) {_root = new Node(kv);_root->_col = BLACK;return true;}// 找到插入位置Node* cur = _root, * parent = nullptr;while (cur){if (cur->_kv.first == kv.first) return false;else if (cur->_kv.first < kv.first) {parent = cur;cur = cur->_right;}else {parent = cur;cur = cur->_left;}}cur = new Node(kv);// 新增节点 颜色优先选择红色cur->_col = RED;if (kv.first > parent->_kv.first) parent->_right = cur;else parent->_left = cur;cur->_parent = parent;// 1、parent不存在,cur就是根了,出去后把根处理成黑的// 2、parent存在,且为黑// 3、parent存在,且为红,继续循环处理// 变色了之后持续网上处理while (parent && parent->_col == RED) // 父亲颜色是红色就需要继续处理(来连续的红节点, 关键看叔叔){Node* grandfather = parent->_parent;if (parent == grandfather->_left) // 父亲在爷爷的左边 右边就是对称的{Node* uncle = grandfather->_right;// g// p uif (uncle && uncle->_col == RED) // 如果叔叔存在且为红色{parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = grandfather->_parent;}else { // 叔叔存在且为黑或者不存在 那么旋转+变色// g// p u// c// 单旋if (cur == parent->_left){RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else {// g// p u// c// 双旋RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break; // 局部根节点是黑色那么就可以退出了}}else {// g// u pNode* uncle = grandfather->_left;if (uncle && uncle->_col == RED) // 如果叔叔存在且为红色{parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = grandfather->_parent;}else { // 叔叔存在且为黑或者不存在 那么旋转+变色// g// u p// c// 单旋if (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else {// g// u p// c// 双旋RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break; // 局部根节点是黑色那么就可以退出了}}}_root->_col = BLACK;return true;}
五:🔥 红黑树的验证
红黑树的检测分为两步:
- 检测其是否满足二叉搜索树(中序遍历是否为有序序列)
- 检测其是否满足红黑树的性质
具体代码如下:
bool IsBalance(){if (_root == nullptr)return true;if (_root->_col == RED){return false;}// 参考值int refNum = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){++refNum;}cur = cur->_left;}return Check(_root, 0, refNum);}bool Check(Node* root, int blackNum, const int refNum){if (root == nullptr){//cout << blackNum << endl;if (refNum != blackNum){cout << "存在黑色节点的数量不相等的路径" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << root->_kv.first << "存在连续的红色节点" << '\n';return false;}if (root->_col == BLACK){blackNum++;}return Check(root->_left, blackNum, refNum) && Check(root->_right, blackNum, refNum);}
六:🔥 红黑树的完整代码
#pragma once#include <iostream>
#include <algorithm>
#include <cstring>
#include <set>
#include <map>
#include <assert.h>using namespace std;enum Color
{RED,BLACK
};template<class K, class V>
struct RBTreeNode {pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent; Color _col;RBTreeNode(const pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr){}
};template<class K, class V>
class RBTree {typedef RBTreeNode<K, V> Node;
public:RBTree() = default;RBTree(const RBTree<K, V>& t){_root = Copy(t._root);}RBTree<K, V>& operator=(RBTree<K, V> t){swap(_root, t._root);return *this;}~RBTree(){Destroy(_root);_root = nullptr;}bool Insert(const pair<K, V>& kv){if (_root == nullptr) {_root = new Node(kv);_root->_col = BLACK;return true;}// 找到插入位置Node* cur = _root, * parent = nullptr;while (cur){if (cur->_kv.first == kv.first) return false;else if (cur->_kv.first < kv.first) {parent = cur;cur = cur->_right;}else {parent = cur;cur = cur->_left;}}cur = new Node(kv);// 新增节点 颜色优先选择红色cur->_col = RED;if (kv.first > parent->_kv.first) parent->_right = cur;else parent->_left = cur;cur->_parent = parent;// 1、parent不存在,cur就是根了,出去后把根处理成黑的// 2、parent存在,且为黑// 3、parent存在,且为红,继续循环处理// 变色了之后持续网上处理while (parent && parent->_col == RED) // 父亲颜色是红色就需要继续处理(来连续的红节点, 关键看叔叔){Node* grandfather = parent->_parent;if (parent == grandfather->_left) // 父亲在爷爷的左边 右边就是对称的{Node* uncle = grandfather->_right;// g// p uif (uncle && uncle->_col == RED) // 如果叔叔存在且为红色{parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = grandfather->_parent;}else { // 叔叔存在且为黑或者不存在 那么旋转+变色// g// p u// c// 单旋if (cur == parent->_left){RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else {// g// p u// c// 双旋RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break; // 局部根节点是黑色那么就可以退出了}}else {// g// u pNode* uncle = grandfather->_left;if (uncle && uncle->_col == RED) // 如果叔叔存在且为红色{parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = grandfather->_parent;}else { // 叔叔存在且为黑或者不存在 那么旋转+变色// g// u p// c// 单旋if (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else {// g// u p// c// 双旋RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break; // 局部根节点是黑色那么就可以退出了}}}_root->_col = BLACK;return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_kv.first < key){cur = cur->_right;}else if (cur->_kv.first > key){cur = cur->_left;}else{return cur;}}return nullptr;}Node* Copy(Node * root){if (root == nullptr)return nullptr;Node* newRoot = new Node(root->_kv);newRoot->_left = Copy(root->_left);newRoot->_right = Copy(root->_right);return newRoot;}void Destroy(Node * root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;}void InOrder(){_InOrder(_root);}int Height(){return _Height(_root);}// 检查是否是红黑树bool IsBalance(){if (_root == nullptr)return true;if (_root->_col == RED){return false;}// 参考值int refNum = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){++refNum;}cur = cur->_left;}return Check(_root, 0, refNum);}private:bool Check(Node* root, int blackNum, const int refNum){if (root == nullptr){//cout << blackNum << endl;if (refNum != blackNum){cout << "存在黑色节点的数量不相等的路径" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << root->_kv.first << "存在连续的红色节点" << '\n';return false;}if (root->_col == BLACK){blackNum++;}return Check(root->_left, blackNum, refNum) && Check(root->_right, blackNum, refNum);}int _Size(Node* root){return root == nullptr ? 0 : _Size(root->_left) + _Size(root->_right) + 1;}int _Height(Node* root){if (root == nullptr)return 0;int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}void RotateL(Node * parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL) subRL->_parent = parent;Node* parent_parent = parent->_parent;subR->_left = parent;parent->_parent = subR;if (parent_parent == nullptr){_root = subR;subR->_parent = nullptr;}else {if (parent == parent_parent->_left) parent_parent->_left = subR;else parent_parent->_right = subR;subR->_parent = parent_parent;}}void RotateR(Node * parent){Node* subL = parent->_left;Node* subLR = parent->_left->_right;parent->_left = subLR;if (subLR) subLR->_parent = parent;Node* parent_parent = parent->_parent;subL->_right = parent;parent->_parent = subL;if (parent_parent == nullptr){_root = subL;subL->_parent = nullptr;}else {if (parent == parent_parent->_left){parent_parent->_left = subL;}else {parent_parent->_right = subL;}subL->_parent = parent_parent;}}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << '\n';_InOrder(root->_right);}Node* _root = nullptr;};void TestRBTree1()
{RBTree<int, int> t;int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };// int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };for (auto e : a){t.Insert({ e, e });}t.InOrder();cout << t.IsBalance() << endl;
}
以上就是红黑树的讲解与完整实现过程,红黑树因为其自平衡的特性,及通过节点颜色来操作其树形结构的特点,极大的提高了数据存储及处理的效率,需要我们好好掌握,觉得这篇博客对你有帮助的,可以点赞收藏关注支持一波~😉

相关文章:

【C++高阶数据结构】红黑树:全面剖析与深度学习
目录 🚀 前言:红黑树与AVL树的比较一: 🔥 红黑树的概念二: 🔥 红黑树的性质 三: 🔥 红黑树节点的定义和结构🚀 3.1 基本元素🚀 3.2 节点颜色🚀 3.…...

前端基于 axios 实现批量任务调度管理器 demo
一、背景介绍 这是一个基于 axios 实现的批量任务调度管理器的 demo。它使用了axios、promise 等多种技术和原理来实现批量处理多个异步请求,并确保所有请求都能正确处理并报告其状态。 假设有一个场景:有一个任务列表,有单个任务的处理功能…...

Docker容器下面home assistant忘记账号密码怎么重置?
环境: docker ha 问题描述: Docker容器下面home assistant忘记账号密码怎么重置? 解决方案: 你可以按照以下步骤来找回或重置密码: 方法一 (未解决) 停止并删除当前的Home Assistant容器(确保你已经保…...

CTF-NSSCTF[GKCTF 2021]
[GKCTF 2021]easycms 考察: 用扫描工具扫描目录,扫描到后台登录界面/admin.php 题目提示了密码是五位弱口令,试了试弱口令admin和12345直接成功了 任意文件下载 点击设计-->主题然后随便选择一个主题,点击自定义࿰…...

MSA+抑郁症模型总结(一)(论文复现)
MSA抑郁症模型总结(一)(论文复现) 本文所涉及所有资源均在传知代码平台可获取 文章目录 MSA抑郁症模型总结(一)(论文复现)情感分析在多场景的应用一、概述二、论文地址三、研究背景四…...

STM32智能农业灌溉系统教程
目录 引言环境准备智能农业灌溉系统基础代码实现:实现智能农业灌溉系统 4.1 数据采集模块 4.2 数据处理与分析模块 4.3 通信与网络系统实现 4.4 用户界面与数据可视化应用场景:农业监测与优化问题解决方案与优化收尾与总结 1. 引言 智能农业灌溉系统通…...

MySQL存储引擎和
MySQL存储引擎 在数据库中保存的是一张张有着千丝万缕关系的表,所以表设计的好坏,将直接影响着整个数据库。而在设计表的时候,最关注的一个问题是使用什么存储引擎。MySQL中的数据用各种不同的技术存储在文件(或者内存)中。这些技术中的每一种…...

Eclipse 主网向开发者开放
摘要:Eclipse 基金会宣布,Eclipse 主网已经向开发者开放。在接下来几周的时间里,Eclipse 将邀请开发者在主网上部署项目,并参加黑客马拉松活动——“Total Eclipse Challenge”。 Eclipse 是首个基于以太坊的 SVM Layer2 方案&am…...
国内NAT服务器docker方式搭建rustdesk服务
前言 如果遇到10054,就不要设置id服务器!!! 由于遇到大带宽,但是又贵,所以就NAT的啦,但是只有ipv4共享和一个ipv6,带宽50MB(活动免费会升130MB~) https://bigchick.xyz/aff.php?aff322 月付-5 循环 :CM-CQ-Monthly-5 年付-60循环:CM-CQ-Annually-60官方…...

锅总浅析链路追踪技术
链路追踪是什么?常用的链路追踪工具有哪些?它们的异同、架构、工作流程及关键指标有哪些?希望读完本文能帮您解答这些疑惑! 一、链路追踪简介 链路追踪技术(Distributed Tracing)是一种用于监控和分析分布…...

为什么阿里开发手册不建议使用Date类?
在日常编码中,基本上99%的项目都会有一个DateUtil工具类,而时间工具类里用的最多的就是java.util.Date。 大家都这么写,这还能有问题?? 当你的“默认常识”出现问题,这个打击,就是毁灭性的。 …...
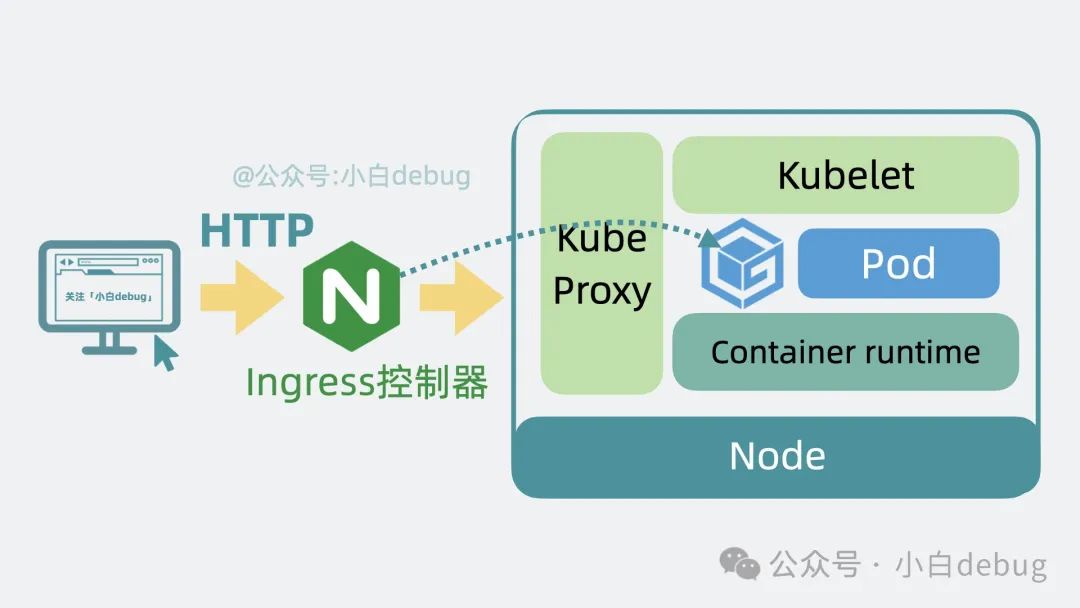
中间层 k8s(Kubernetes) 到底是什么,架构是怎么样的?
你是一个程序员,你用代码写了一个博客应用服务,并将它部署在了云平台上。 但应用服务太过受欢迎,访问量太大,经常会挂。 所以你用了一些工具自动重启挂掉的应用服务,并且将应用服务部署在了好几个服务器上,…...

【CTFWP】ctfshow-web40
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 题目介绍:题目分析:payload:payload解释:payload2:payload2解释:flag 题目介绍: …...

项目实战1(30小时精通C++和外挂实战)
项目实战1(30小时精通C和外挂实战) 01-MFC1-图标02-MFC2-按钮、调试、打开网页05-MFC5-checkbox及按钮绑定对象06--文件格式、OD序列号08-暴力破解09-CE10-秒杀僵尸 01-MFC1-图标 这个外挂只针对植物大战僵尸游戏 开发这个外挂,首先要将界面…...

百日筑基第三十六天
今日论道还算顺利,只可惜感到也没学到什么东西。晚些时候师祖问话,主要是来这边之后有什么困难之类,好像也没遇到需要他来帮我解决的困难,于是问了些修炼方法之类。...

MySQL: ALTER
正文 在数据库管理系统(DBMS)中,DDL(Data Definition Language)、DCL(Data Control Language)、和 DML(Data Manipulation Language)是三种主要的SQL(Struct…...

微前端技术预研 - bit初体验
1.关于什么是微前端以及微前端的发展, 当前主流框架以及实现技术等,可参考这篇总结(非常全面), 微前端总结:目录详见下图 本文内容主要针对bit框架的实时思路以及具体使用。 1.什么是Bit? Bit 是可组合软件的构建…...

对象关系映射---ORM
一、什么是ORM? ORM(Object Relational Mapping),即对象关系映射,是一种程序设计技术,用于在面向对象编程语言中实现对象和关系型数据库之间的映射。 二、ORM是干什么的? ORM 的主要目的是简…...
Authentication)
Django REST Framework(十七)Authentication
1.认证Authentication 在 Django REST framework (DRF) 中,可以在配置文件中配置全局默认的认证方案。常见的认证方式包括 cookie、session、和 token。DRF 提供了灵活的认证机制,可以在全局配置文件中设置默认认证方式,也可以在具体的视图类…...

FPGA开发——数码管的使用
一、概述 在我们的日常开发中,数字显示的领域中用得最多的就是数码管,这篇文章也是围绕数码管的静态显示和动态显示进行一个讲解。 1、理论 (1)数码管原理图 在对数码管进行相关控制时,其实就是对于8段发光二极管和…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

DeepSeek越强,Kimi越慌?
被DeepSeek吊打的Kimi,还有多少人在用? 去年,月之暗面创始人杨植麟别提有多风光了。90后清华学霸,国产大模型六小虎之一,手握十几亿美金的融资。旗下的AI助手Kimi烧钱如流水,单月光是投流就花费2个亿。 疯…...
