吴恩达老师机器学习-ex4
梯度检测没有实现。有借鉴网上的部分
导入相关库,读取数据
因为这次的数据是mat文件,需要使用scipy库中的loadmat进行读取数据。
通过对数据类型的分析,发现是字典类型,查看该字典的键,可以发现又X,y等关键字。
import numpy as np
import scipy.io as sio
from scipy.optimize import minimize
from sklearn.preprocessing import OneHotEncoder#读取数据
path = "./ex4data1.mat"
data = sio.loadmat(path)
# print(type(data))
# print(data.keys())
X = data.get("X")
Y = data.get("y").flatten()
# X = np.insert(X,0,values=1,axis=1)
# print(Y.shape)
# print(Y)one-hot编码
在之前没有涉及神经网络的方向传播等时,可以直接将Y降维。
而在神经网络中需要对Y进行编码,使每一个y值都是一个10维的向量
#one-hot编码
encoder = OneHotEncoder(sparse=False)
Y_onehot = encoder.fit_transform(Y.reshape(-1,1))随机初始化
当使用高级优化算法或者梯度下降算法时,需要对向量进行赋值。
第一种想法是全部设为0,在逻辑回归中,是完全被允许的,但在训练神经网络时,这种初始值起不到任何作用。因为这会导致第二层激活项的值完全相同(因为前一层的权重相同),这个问题称为对称权重问题。
为了解决这个问题,我们采用随机初始化的方法,也就是将每一个都初始化为一个范围在
中的一个随机数。
#初始化参数
input_size = 400
hidden_size = 25
num_labels = 10
lamda = 1size = (input_size+1)*hidden_size+(hidden_size+1)*num_labels
params = np.random.uniform(-1.2,1.2,size)
序列化
因为到后面优化的时候fun和jac参数要求代价函数和梯度的第一个参数必须为一维向量,所以这里需要序列化。
#序列化
def serialize(theta1,theta2):return np.r_[theta1.flatten(),theta2.flatten()]
def deserialize(params):return params[:(input_size+1)*hidden_size].reshape(hidden_size,input_size+1),params[(input_size+1)*hidden_size:].reshape(num_labels,hidden_size+1)theta1,theta2 = deserialize(params)前向传播
同上一题一致的前向传播
#前向传播
def feed_forward(params,X):theta1, theta2 = deserialize(params)a1 = np.insert(X, 0, values=np.ones(X.shape[0]), axis=1)z2 = a1 @ theta1.Ta2 = 1/(1+np.exp(-z2))a2 = np.insert(a2,0,values=1,axis=1)z3 = a2 @ theta2.Th = 1/(1+np.exp(-z3))return a1,z2,a2,z3,h代价函数
不需要正则化
公式如下:

#代价函数
def cost_func(params,X,Y,lamda):theta1, theta2 = deserialize(params)a1,z2, a2, z3, h = feed_forward(params,X)m = len(X)cost = -np.sum(Y * np.log(h) + (1-Y) * np.log(1-h))/mreg = (np.sum(np.power(theta1[:,1:],2)) + np.sum(np.power(theta2[:,1:],2)))* lamda/(2*m)return reg+cost反向传播
相关公式如下:


#反向传播
def sigmoid_gradient(z):return 1/(1+np.exp(-z))*(1-1/(1+np.exp(-z)))def gradientReg(params,X,Y,lamda=1):theta1, theta2 = deserialize(params)m = len(X)a1, z2, a2, z3, h = feed_forward(params,X)delta3 = h - Ydelta2 = delta3 @ theta2[:,1:] * sigmoid_gradient(z2)Delta2 = delta3.T @ a2 / mDelta1 = delta2.T @ a1 / mtheta1[:, 0] = 0theta2[:, 0] = 0regDelta1 = Delta1 + (lamda / m) * theta1regDelta2 = Delta2 + (lamda / m) * theta2return serialize(regDelta1,regDelta2)优化
fmin = minimize(fun=cost_func,x0=params,args=(X,Y_onehot,lamda),method="TNC",jac=gradientReg,options={'maxiter': 400})预测
a1,z2,a2,z3,h = feed_forward(fmin.x,X)
y_pred = np.argmax(h,axis=1)
y_pred = y_pred + 1
acc = np.mean(y_pred==Y)
print(acc)
准确率达到了98.64%
---------------------------------------------------------------------------------------------------------------------------------
可以先将数据可视化,展示手写数字。
def one_image(X):pick_one = np.random.randint(5000)image = X[pick_one,:]fig,ax = plt.subplots()ax.imshow(image.reshape(20,20).T,cmap="gray_r")plt.xticks([])plt.yticks([])plt.show()one_image(X)
def more_image(X):pick_more = np.random.choice(len(X),100)images = X[pick_more,:]fig,ax = plt.subplots(nrows=10,ncols=10, figsize=(8, 8), sharex=True, sharey=True)for i in range(10):for j in range(10):ax[i,j].imshow(images[10*i+j].reshape(20,20).T,cmap="gray_r")plt.xticks([])plt.yticks([])plt.show()
more_image(X)最后可以使用上面写出的函数将隐藏层可视化。
thetafinal1, thetafinal2 = deserialize(fmin.x)
hidden_layer = thetafinal1[:, 1:]
more_image(hidden_layer)相关文章:

吴恩达老师机器学习-ex4
梯度检测没有实现。有借鉴网上的部分 导入相关库,读取数据 因为这次的数据是mat文件,需要使用scipy库中的loadmat进行读取数据。 通过对数据类型的分析,发现是字典类型,查看该字典的键,可以发现又X,y等关…...

C语言-函数例题
函数经典例题 1、编写一个函数实现该功能:从键盘输入一个字串符, 再输入两个正整数 m 和 n, 输出字符串中从 m 开始, 连续 n 个字符。例如, 输入 abcdefg,2,3,输出 bcd. #include <stdio.h> /*作者: zcy日期:功能描述:编写…...

鸿蒙应用框架开发【多HAP】程序框架
多HAP 介绍 本示例展示多HAP开发,简单介绍了多HAP的使用场景,应用包含了一个entry HAP和两个feature HAP,两个feature HAP分别提供了音频和视频播放组件,entry中使用了音频和视频播放组件。 三个模块需要安装三个hap包ÿ…...

PG如何实现跨大版本升级
数据库进行升级,是一个再正常不过的功能,比如功能的需要,遇到BUG,安全漏洞等等,具体升级包含子版本升级,主版本升级。如果用过ORACLE的朋友,一定知道,在ORACLE中,如果要实…...

JDK 8 升级 17 及 springboot 2.x 升级 3.x 指南
JDK 8 升级 17 简介 从 JDK 8 升级到 JDK 17 的过程中,有几个主要的变化,特别是 Java Platform Module System (JPMS) 的引入,以及一些包路径的调整。以下是与 JDK 17 相关的一些重要变化: Java Platform Module System (JPMS) …...

基于java的人居环境整治管理系统(源码+lw+部署文档+讲解等)
前言 💗博主介绍:✌全网粉丝20W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java、小程序技术领域和毕业项目实战✌💗 👇🏻…...

深入了解Pip:Python包管理器的详细指南
目录 Pip简介Pip的安装与升级Pip的基本使用 安装包卸载包列出已安装的包查看包的信息 管理依赖 使用requirements.txt冻结当前环境的包 Pip进阶用法 安装特定版本的包使用代理安装包从本地文件安装包 创建和发布Python包 创建一个Python包编写setup.py文件发布到PyPI 常见问题…...

Corsearch 用 ClickHouse 替换 MySQL 进行内容和品牌保护
本文字数:3357;估计阅读时间:9 分钟 作者:ClickHouse Team 本文在公众号【ClickHouseInc】首发 Chase Richards 自 2011 年在初创公司 Marketly 担任工程负责人,直到 2020 年公司被收购。他现在是品牌保护公司 Corsear…...

常见的应急救援设备有哪些_鼎跃安全
在我们的生活中,应急事件的发生常常是突如其来的,它们对人民的生命财产安全构成重大威胁,同时也对社会稳定提出严峻挑战。在这样的紧急情况下,迅速开展有效的救援工作显得尤为重要。而在整个救援过程中,应急设备的使用…...

Vue 项目部署后首页白屏问题排查与解决
引言 在部署 Vue.js 项目时,有时会遇到首页加载后出现白屏的情况,这可能是由于多种原因造成的。本文将介绍一些常见的排查方法和解决方案,帮助开发者快速定位问题并解决。 1. 常见原因分析 首页白屏的问题可能由以下几个方面的原因导致&am…...

STM32 定时器移相任意角度和占空比,频率可调
由于使用了中断修改翻转的CCR值,对于频率超250K以上不太适用. void Motor1_Init(Motor MotorChValue) { GPIO_InitTypeDef GPIO_InitStructure;TIM_TimeBaseInitTypeDef TIM_TimeBaseStructure;TIM_OCInitTypeDef TIM_OCInitStructure;NVIC_InitTypeDef NVIC_Ini…...

C++ 与其他编程语言区别_C++11/14/17新特性总结
C11 decltype类型推导 decltype不依赖于初始化,根据表达式类推导类型 auto b :根据右边a的初始值来推导出变量的类型,然后将该初始值赋给bdecltype 则是根据a表达式来推导类型,变量的初始值与表达式的值无关表达式类型注意点&…...

玩转云服务:Google Cloud谷歌云永久免费云服务器「白嫖」 指南
前几天,和大家分享了: 玩转云服务:Oracle Cloud甲骨文永久免费云服务器注册及配置指南 相信很多同学都卡在了这一步: 可用性域 AD-1 中配置 VM.Standard.E2.1.Micro 的容量不足。请在其他可用性域中创建实例,或稍后…...

用18讲必看:宇哥亲划重点内容+核心题总结
25考研结束之后,张宇老师的风评可能会两极分化 其中一波把张宇老师奉为考研数学之神,吹捧「三向解题法」天下无敌。 另外一波对张宇老师的评价负面,在网上黑张宇老师! 为什么会这么说,因为张宇老师的新版36讲争议太…...

什么是安全生产痕迹化管理?如何做到生产过程中全程痕迹化管理?
安全生产痕迹化管理,简单来说,就是通过记录一些“信息”来确保安全工作的进展。这些方法包括记会议内容、写安全日记、拍照片、签字盖章、指纹识别、面部识别还有手机定位等。记录下来的文字、图片、数据和视频,就像一个个“脚印”࿰…...

VIsual Studio:为同一解决方案下多个项目分别指定不同的编译器
一、引言 如上图,我有一个解决方案【EtchDevice】,他包含两个(甚至更多个)子项目,分别是【DeviceRT】和【DeviceWin】,见名知意,我需要一个项目编译运行在RTOS上,譬如一个名叫INTime…...
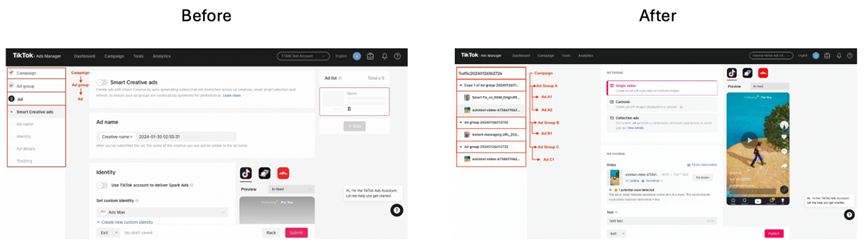
Flat Ads资讯:Meta、Google、TikTok 7月产品政策速递
Flat Ads拥有全球媒介采买(MediaBuy)业务,为方便广告主及时了解大媒体最新政策,Flat Ads将整理大媒体产品更新月报,欢迎大家关注我们及时了解最新行业动向。 一、Meta 1、Reels 应用推广现可突出显示应用评分、点评和下载量 为了不断优化 Instagram 上的广告体验和广告表现,…...

嵌入式C++、ROS 、OpenCV、SLAM 算法和路径规划算法:自主导航的移动机器人流程设计(代码示例)
在当今科技迅速发展的背景下,嵌入式自主移动机器人以其广泛的应用前景和技术挑战吸引了越来越多的研究者和开发者。本文将详细介绍一个嵌入式自主移动机器人项目,涵盖其硬件与软件系统设计、代码实现及项目总结,并提供相关参考文献。 项目概…...

数据安全堡垒:SQL Server数据库备份验证与测试恢复全攻略
数据安全堡垒:SQL Server数据库备份验证与测试恢复全攻略 在数据库管理中,备份是确保数据安全的关键环节,但仅仅拥有备份是不够的,验证备份的有效性并能够从备份中成功恢复数据同样重要。SQL Server提供了一系列的工具和方法来执…...

嵌入式人工智能(40-基于树莓派4B的水滴传感器和火焰传感器)
虽然这两个传感器水火不容,我还是把他们放到一起了。本文是有线传感器的最后一个部分了。后面如果还有文章介绍有线传感器,也是补充学习其他内容不得已而为之。如果不是,就当我没说,哈哈。 1、水滴传感器 水滴传感器又称雨滴传感…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
