如何在Unity中实现AStar寻路算法及地图编辑器
文章目录
- AStar算法
- 简介
- 实现
- Node节点
- 节点间的估价
- 算法核心
- 邻节点的搜索方式
- 地图编辑器
- 简介
- 实现
- 绘制地图网格
- 障碍/可行走区域
- 地图数据存储
AStar算法
简介
Unity中提供了NavMesh导航寻路的AI功能,如果项目不涉及服务端它应该能满足大部分需求,但如果涉及服务端且使用状态同步技术,可能需要服务端同时实现寻路功能,这时就需要考虑其它实现思路,而AStar寻路算法则是常使用的一种。
AStar算法是一种静态路网中求解最短路径最有效的直接搜索方法,基于广度优先搜索(BFS)和Dijkstra算法,通过不断维护节点的代价来寻求代价最小的路径,代价的估价公式:F(N)=G(N) + H(N)。
- G:理解为起始节点到当前节点的代价;
- H:理解为当前节点到终节点的代价。
其它概念:
- 开放集合:记录所有被考虑用来寻找最短路径的节点集合;
- 封闭集合:记录不会被考虑用来寻找最短路径的节点集合。
算法思路:
- 将起始节点放入开放集合;
- While循环重复以下步骤,直到结束条件满足:
- 在开放集合中寻找代价最小的节点,并把寻找到的节点作为Current当前节点;
- 将获取到的当前节点从开放集合移除放入封闭集合;
- 若当前节点已经是终节点,寻路结束,跳出While循环,否则继续执行以下操作;
- 获取当前节点的邻节点,并对每个邻节点执行以下步骤:
- 若邻节点为不可行走区域(障碍)或者邻节点已经在封闭集合中,不执行任何操作,Continue继续遍历下一个邻节点;
- 若邻节点不在开放集合中,将其放入开放集合,并将Current当前节点赋值给该邻节点的父节点,计算、记录该邻节点的G、H代价;
- 若邻节点在开放集合中,判断经Current当前节点到达该邻节点的G值是否小于原来的G值,若小于则将该邻节点的父节点设为当前节点,并重新计算该邻节点的G、H代价。
- 从终节点开始依次获取父节点放入一个列表,最终将列表做倒序操作就是最终寻路的路径。
实现
Node节点
地图网格由x * y个Node节点组成,定义节点类,变量包含节点的x、y索引值、父节点信息、G、H、F代价值以及是否为可行走区域的标识信息,代码如下:
namespace SK.Framework.AStar
{public class Node{public int x;public int y;/// <summary>/// 父节点/// </summary>public Node parent;/// <summary>/// 是否为可行走区域/// </summary>public bool IsWalkable { get; private set; }/// <summary>/// 起始节点到当前节点的代价/// </summary>public int gCost;/// <summary>/// 当前节点到终节点的代价/// </summary>public int hCost;/// <summary>/// 代价/// </summary>public int Cost { get { return gCost + hCost; } }public Node(int x, int y, bool isWalkable){this.x = x;this.y = y;IsWalkable = isWalkable;}}
}
节点间的估价
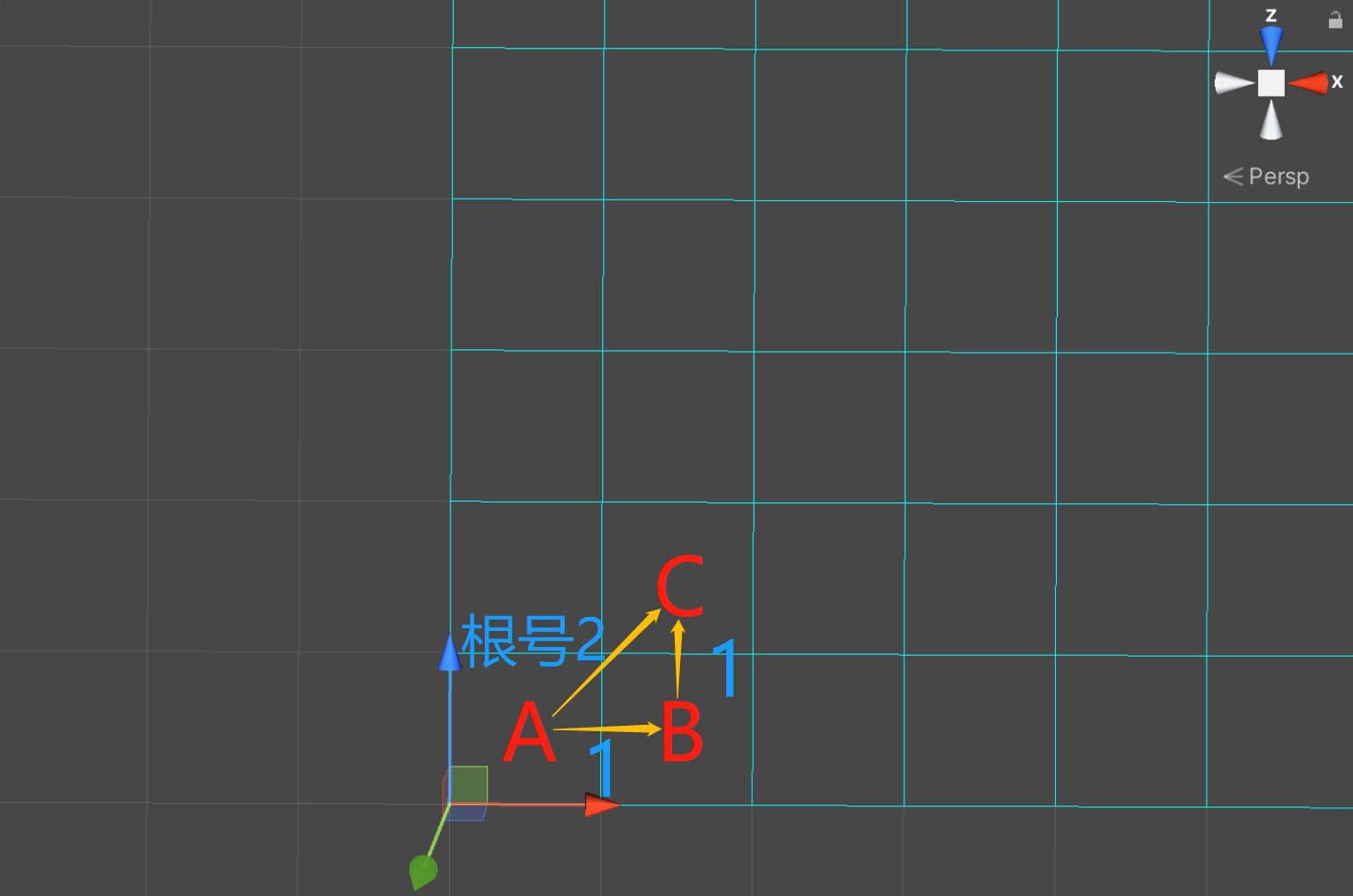
每向正上、下、左右方向走一步代价为1,根据勾股定理,每向斜方向走一步代价为2\sqrt{2}2,近似1.414,而为了便于计算、节省性能,我们将正方向移动一步的代价记为10,斜方向移动一步的代价记为14,都取int整数。
//计算两节点之间的代价
private int CalculateCost(Node n1, Node n2)
{//绝对值int deltaX = n1.x - n2.x;if (deltaX < 0) deltaX = -deltaX;int deltaY = n1.y - n2.y;if (deltaY < 0) deltaY = -deltaY;int delta = deltaX - deltaY;if (delta < 0) delta = -delta;//每向正上、下、左、右方向走一步代价增加10//每斜向走一步代价增加14(勾股定理,精确来说是近似14.14~)return 14 * (deltaX > deltaY ? deltaY : deltaX) + 10 * delta;
}
算法核心
/// <summary>
/// 根据起始节点和终节点获取路径
/// </summary>
/// <param name="startNode">起始节点</param>
/// <param name="endNode">终节点</param>
/// <returns>路径节点集合</returns>
public List<Node> GetPath(Node startNode, Node endNode)
{//开放集合List<Node> openCollection = new List<Node>();//封闭集合HashSet<Node> closeCollection = new HashSet<Node>();//起始节点放入开放集合openCollection.Add(startNode);//开放集合中数量为0时 寻路结束while (openCollection.Count > 0){//当前节点Node currentNode = openCollection[0];//遍历查找是否有代价更小的节点//若代价相同,选择移动到终点代价更小的节点for (int i = 1; i < openCollection.Count; i++){currentNode = (currentNode.Cost > openCollection[i].Cost|| (currentNode.Cost == openCollection[i].Cost&& currentNode.hCost > openCollection[i].hCost))? openCollection[i] : currentNode;}//将获取到的当前节点从开放集合移除放入封闭集合openCollection.Remove(currentNode);closeCollection.Add(currentNode);//当前节点已经是终节点 寻路结束if (currentNode == endNode)break;//获取邻节点List<Node> neighbourNodes = GetNeighbouringNodes(currentNode, SearchMode.Link8);//在当前节点向邻节点继续搜索for (int i = 0; i < neighbourNodes.Count; i++){Node neighbourNode = neighbourNodes[i];//判断邻节点是否为不可行走区域(障碍)或者邻节点已经在封闭集合中if (!neighbourNode.IsWalkable || closeCollection.Contains(neighbourNode))continue;//经当前节点到达该邻节点的G值是否小于原来的G值//或者该邻节点还没有放入开放集合,将其放入开放集合int cost = currentNode.gCost + CalculateCost(currentNode, neighbourNode);if (cost < neighbourNode.gCost || !openCollection.Contains(neighbourNode)){neighbourNode.gCost = cost;neighbourNode.hCost = CalculateCost(neighbourNode, endNode);neighbourNode.parent = currentNode;if (!openCollection.Contains(neighbourNode))openCollection.Add(neighbourNode);}}}//倒序获取父节点List<Node> path = new List<Node>();Node currNode = endNode;while (currNode != startNode){path.Add(currNode);currNode = currNode.parent;}//再次倒序后得到完整路径path.Reverse();return path;
}
邻节点的搜索方式
搜索邻节点时有两种搜索方式,四连通和八连通:
- 四连通:又称四邻域,是指对应节点的上、下、左、右四个方向为邻节点:
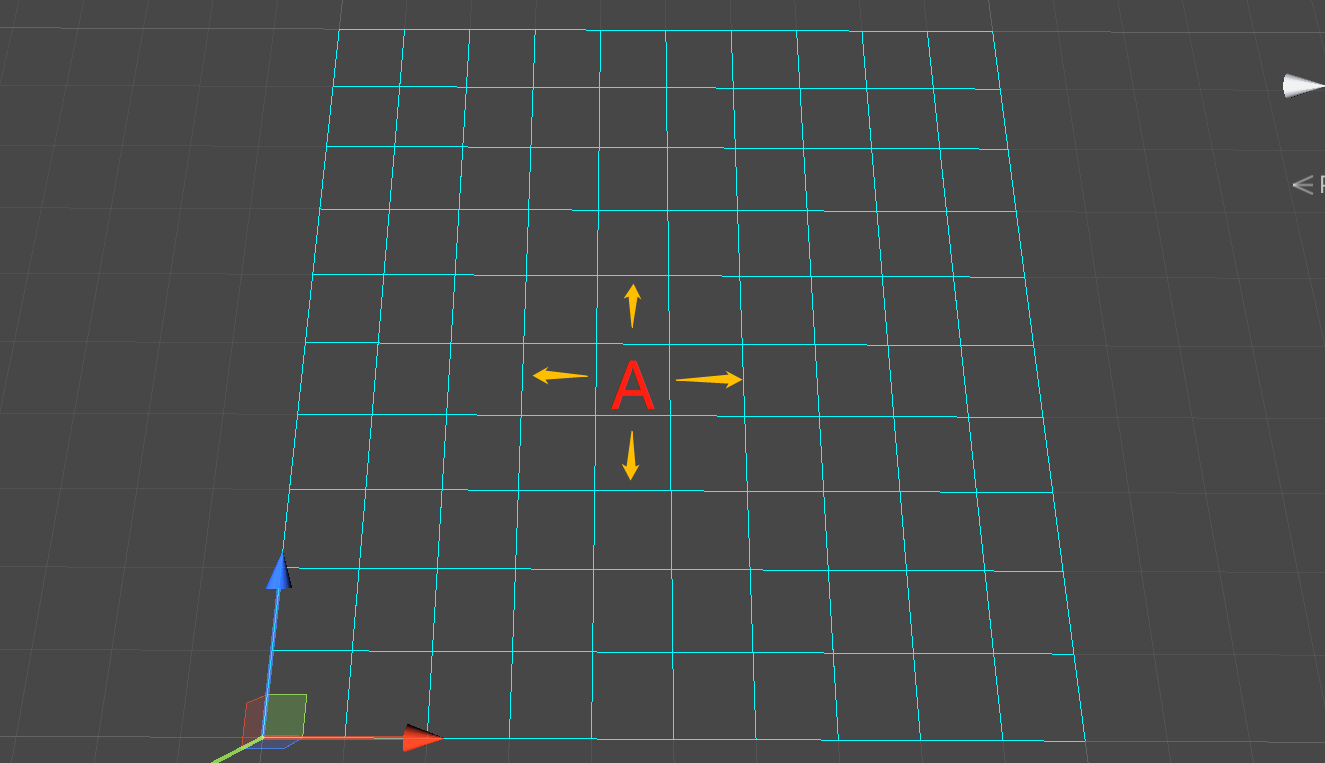
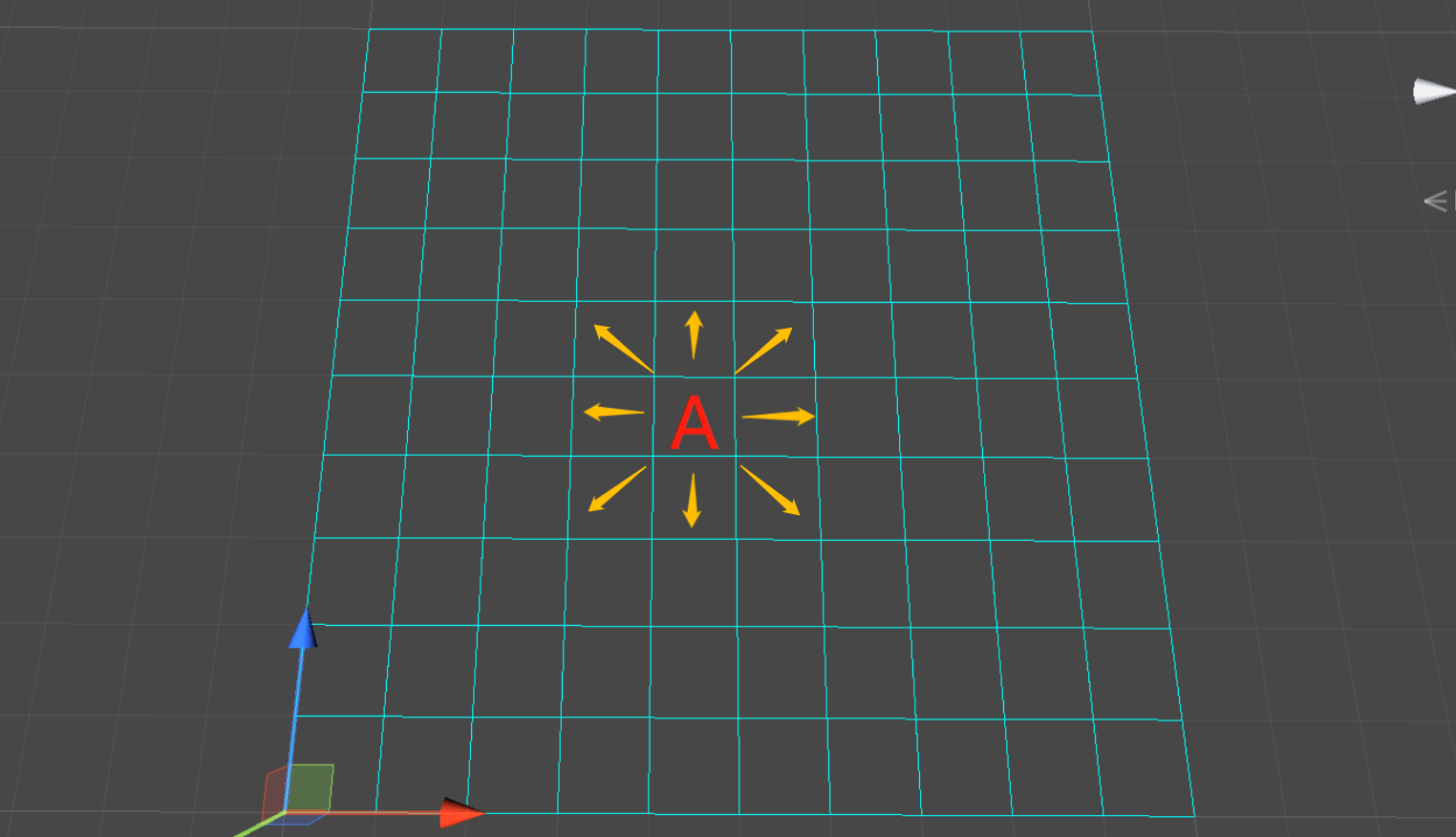
- 八连通:又称八邻域,是指对应节点的上、下、左、右、左上、右上、左下、右下八个方向为邻节点:
/// <summary>
/// 获取指定节点的邻节点
/// </summary>
/// <param name="node">指定节点</param>
/// <param name="searchMode">搜索方式 四连通/八连通</param>
/// <returns>邻节点列表</returns>
public List<Node> GetNeighbouringNodes(Node node, SearchMode searchMode)
{List<Node> neighbours = new List<Node>();switch (searchMode){case SearchMode.Link4:for (int i = -1; i <= 1; i++){if (i == 0) continue;int x = node.x + i;if (x >= 0 && x < this.x)neighbours.Add(nodesDic[x * this.x + node.y]);int y = node.y + i;if (y >= 0 && y < this.y)neighbours.Add(nodesDic[node.x * this.x + y]);}break;case SearchMode.Link8:for (int i = -1; i <= 1; i++){for (int j = -1; j <= 1; j++){if (i == 0 && j == 0) continue;int x = node.x + i;int y = node.y + j;if (x >= 0 && x < this.x && y >= 0 && y < this.y)neighbours.Add(nodesDic[x * this.x + y]);}}break;}return neighbours;
}
地图编辑器
简介
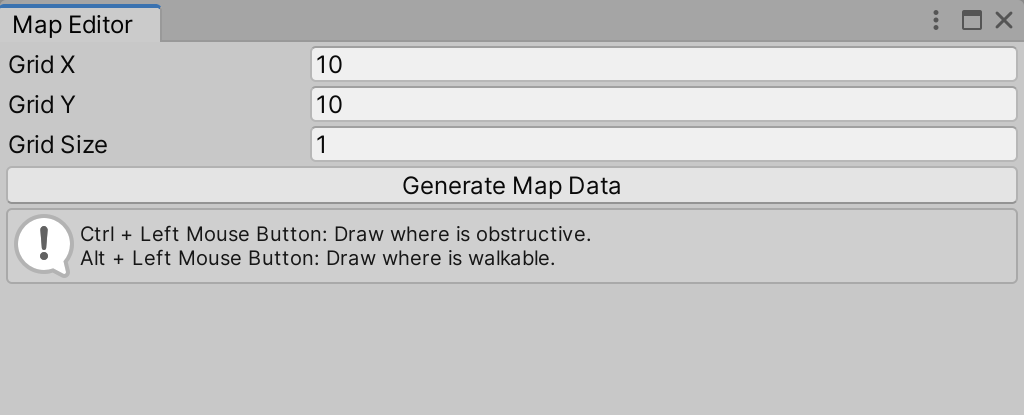
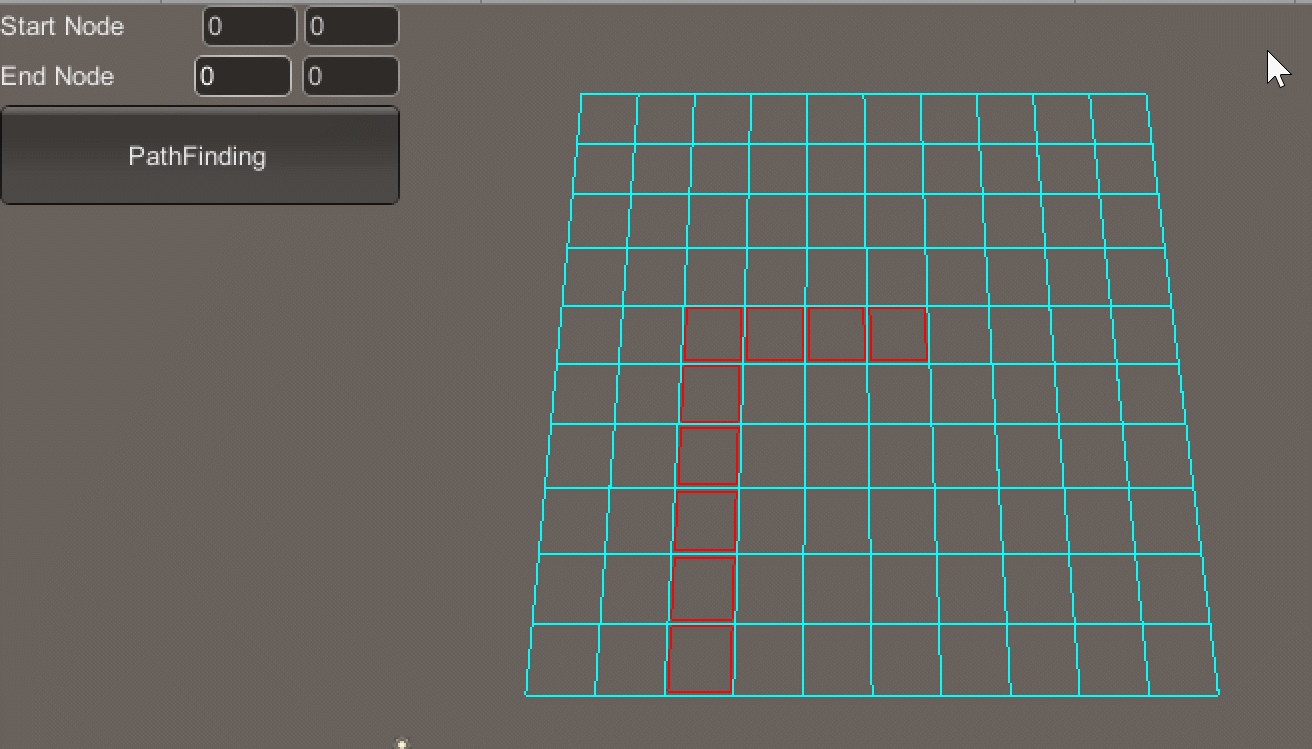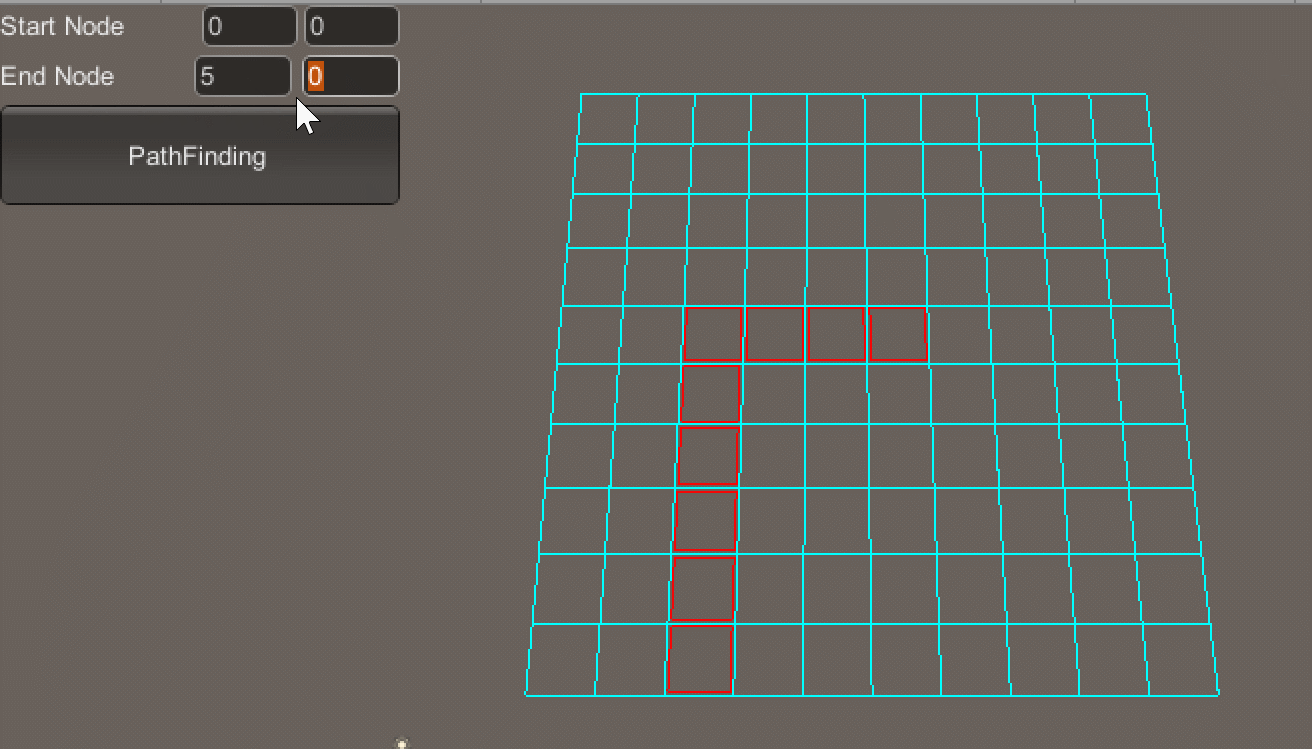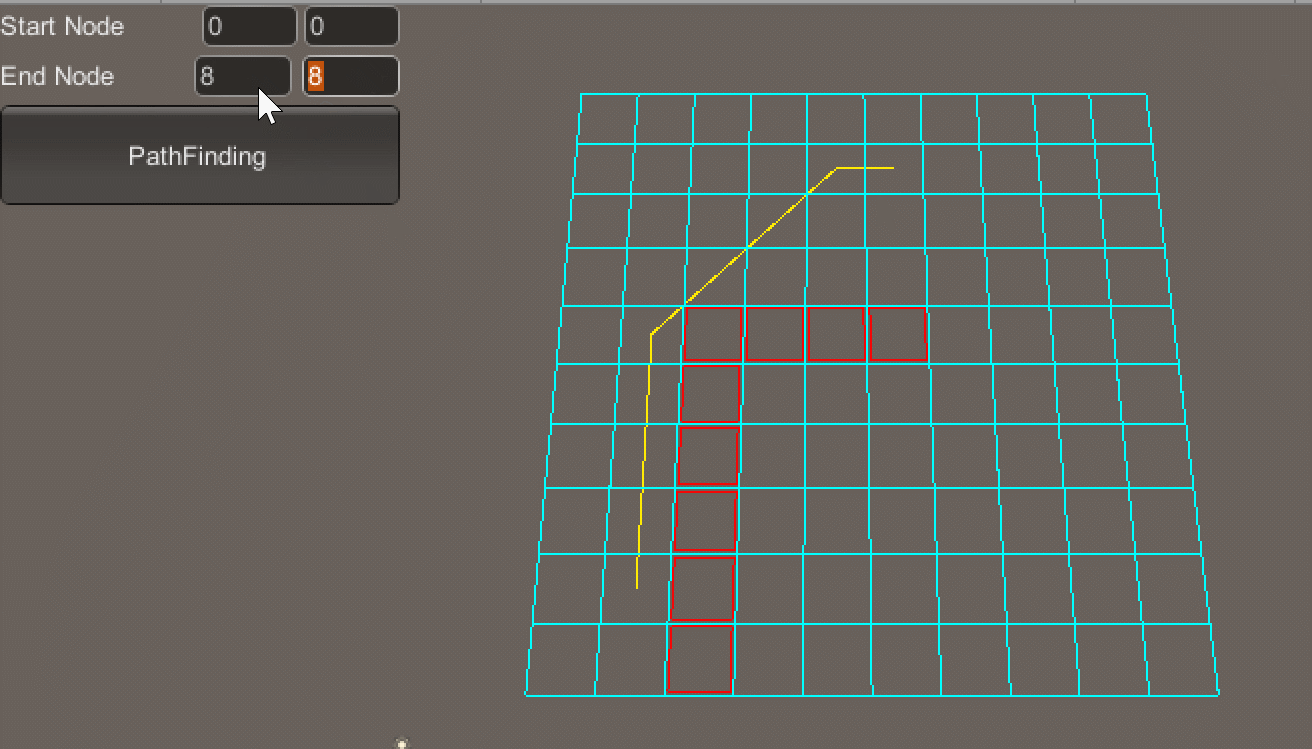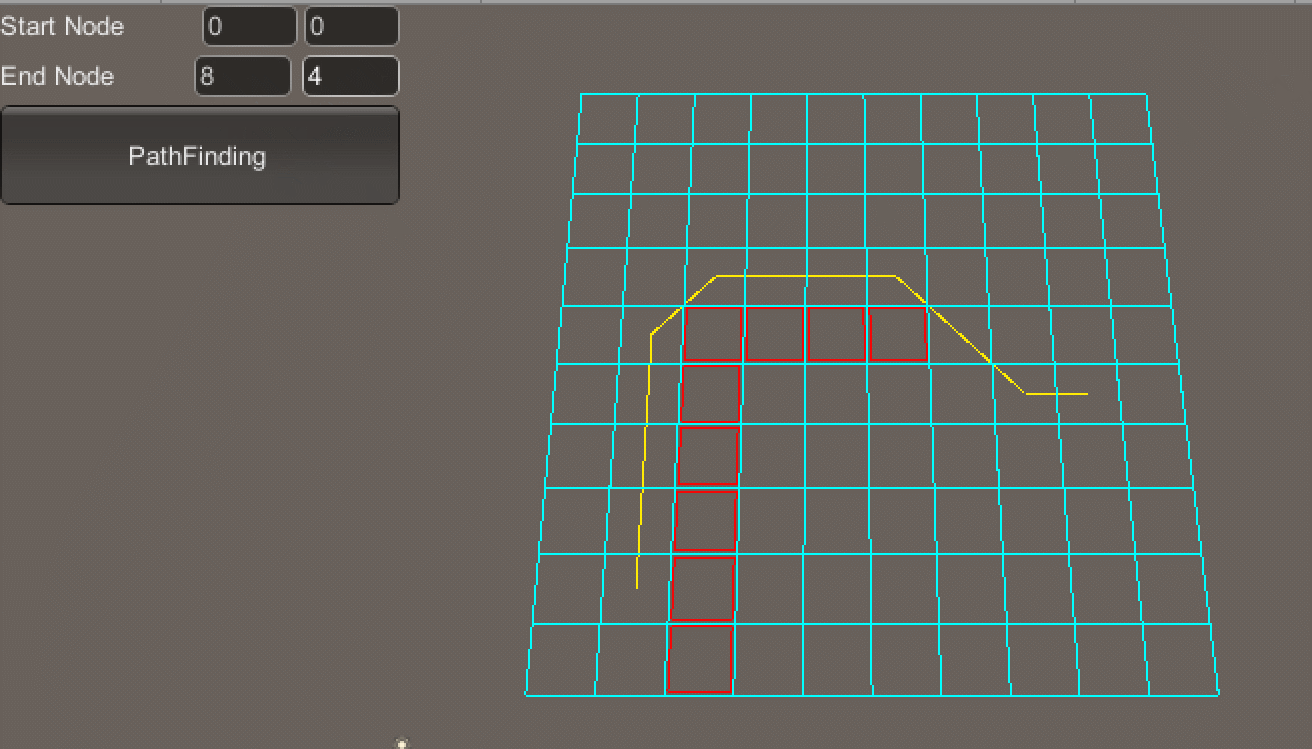
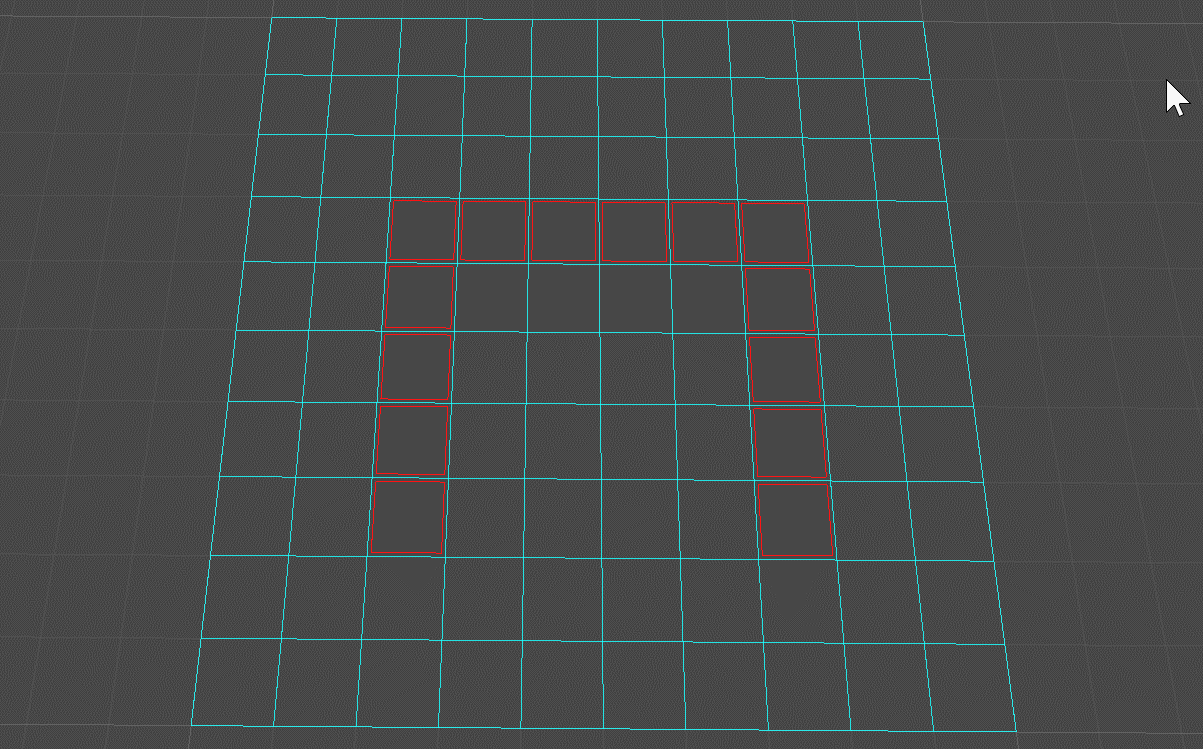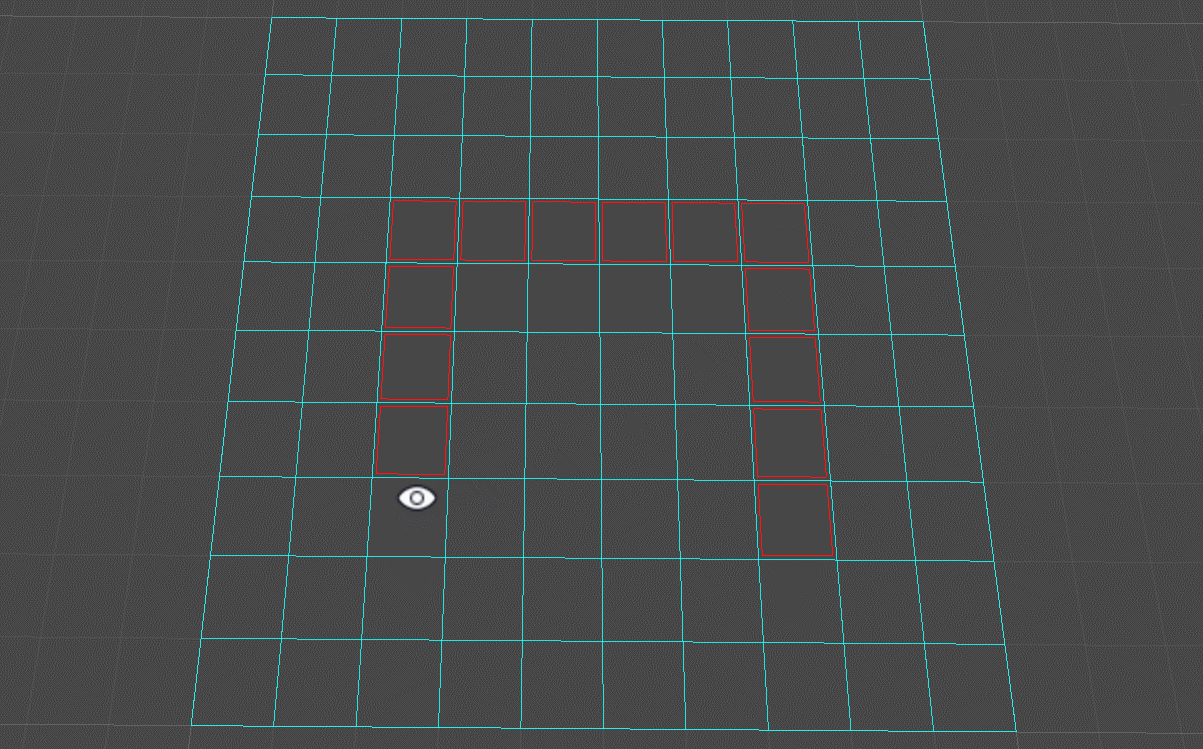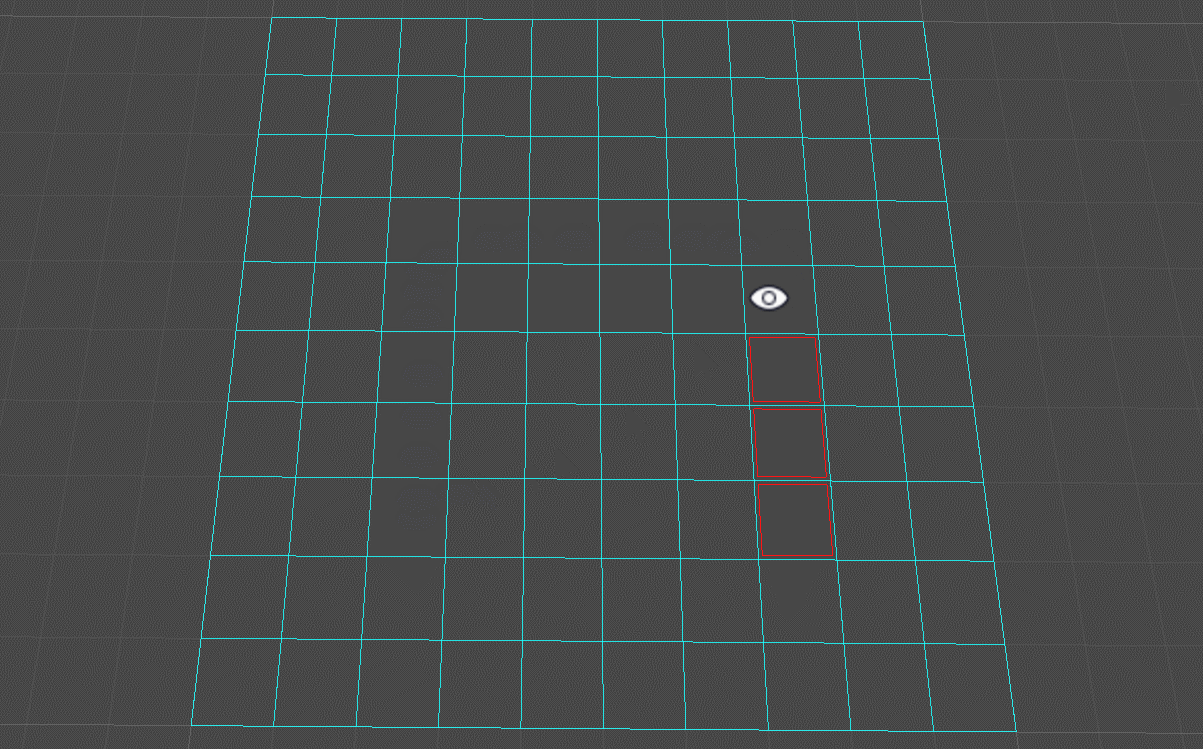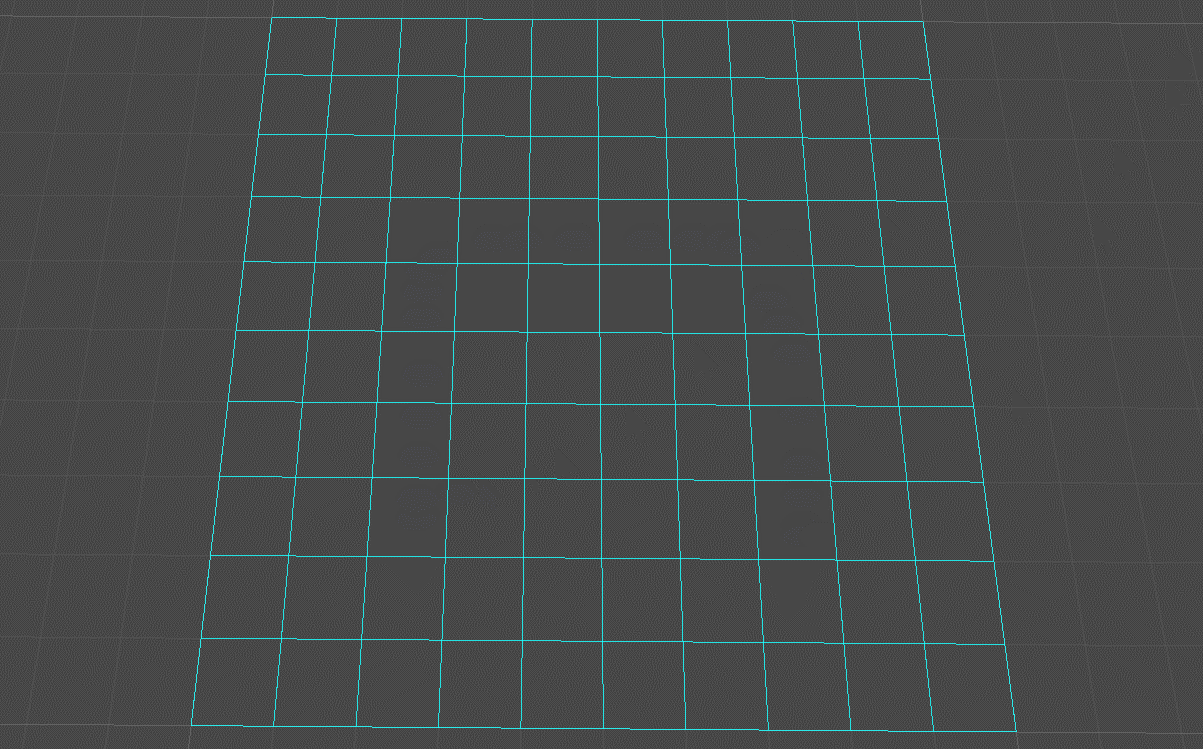
按住Ctrl + 鼠标左键绘制地图障碍区域(如图所示,红色框区域即为障碍区域):

按住Alt + 鼠标左键绘制地图可行走区域(清除障碍区域):
实现
绘制地图网格
Grid X、Y组成地图网格(x * y);Grid Size指定每个网格(节点)的大小:
//绘制地图网格
Handles.color = Color.cyan;
for (int i = 0; i <= x; i++)
{Vector3 start = i * size * Vector3.right;Vector3 end = start + y * size * Vector3.forward;Handles.DrawLine(start, end);
}
for (int i = 0; i <= y; i++)
{Vector3 start = i * size * Vector3.forward;Vector3 end = start + x * size * Vector3.right;Handles.DrawLine(start, end);
}
障碍/可行走区域
使用二维数组bool[,] map存储各节点网格是否为可行走区域
Ctrl + 鼠标左键标识障碍区域;Alt + 鼠标左键标识可行走区域:
HandleUtility.AddDefaultControl(GUIUtility.GetControlID(FocusType.Passive));
//Ctrl + 鼠标左键 绘制障碍区域
//Alt + 鼠标左键 绘制可行走区域
var e = Event.current;
if (e != null && (e.control || e.alt) && (e.type == EventType.MouseDown || e.type == EventType.MouseDrag) && e.button == 0)
{Ray ray = HandleUtility.GUIPointToWorldRay(e.mousePosition);if (Physics.Raycast(ray, out RaycastHit hit)){int targetX = Mathf.CeilToInt(hit.point.x / size);int targetY = Mathf.CeilToInt(hit.point.z / size);if (targetX <= x && targetX > 0 && targetY <= y && targetY > 0){map[targetX - 1, targetY - 1] = !e.control;}}e.Use();
}//红色框绘制障碍区域
Handles.color = Color.red;
for (int m = 0; m < x; m++)
{for (int n = 0; n < y; n++){if (!map[m, n])Handles.DrawWireCube(new Vector3(m * size, 0f, n * size) + .5f * size * (Vector3.forward + Vector3.right), .9f * size * (Vector3.forward + Vector3.right));}
}
地图数据存储
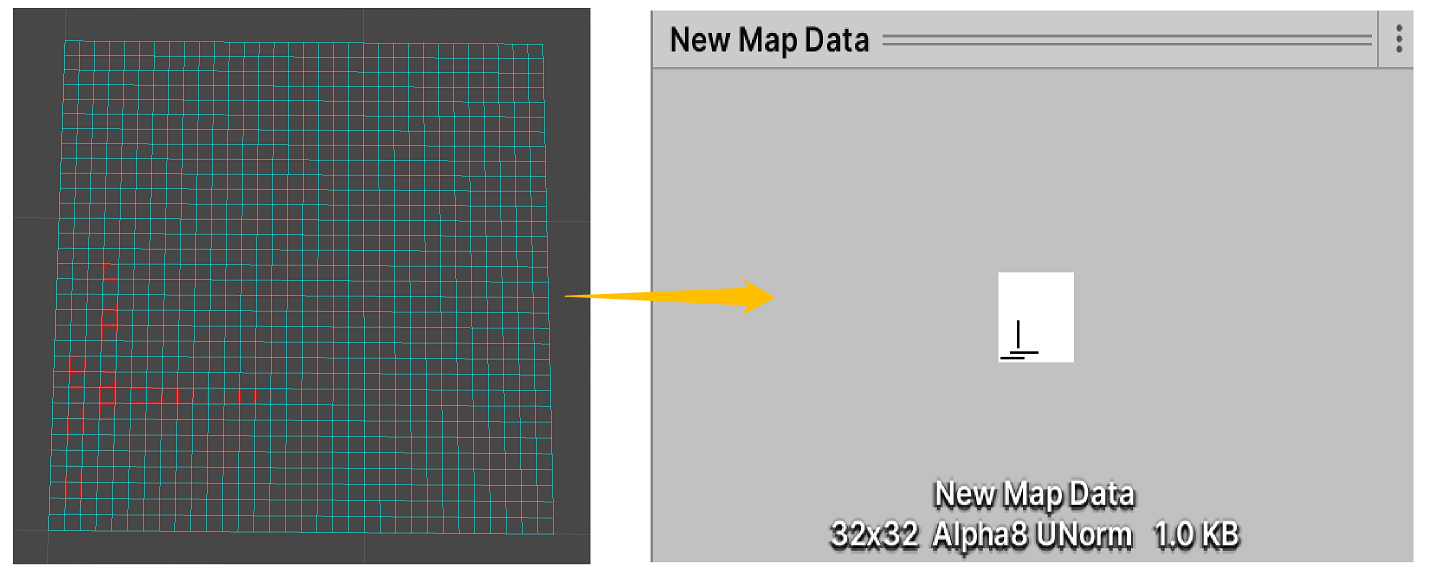
由于地图数据存储于bool[,] map二维数组中,不支持序列化,因此将其转化为存储于Texture2D类型资产中,实现方式如下:
//生成地图
if (GUILayout.Button("Generate Map Data"))
{//选择保存路径string filePath = EditorUtility.SaveFilePanel("Save Map Data", Application.dataPath, "New Map Data", "asset");if (!string.IsNullOrEmpty(filePath)){//转化为Asset路径filePath = filePath.Substring(filePath.IndexOf("Assets"));//创建地图TexTexture2D bitmap = new Texture2D(x, y, TextureFormat.Alpha8, false);byte[] bytes = bitmap.GetRawTextureData();//默认全部为可行走区域for (int i = 0; i < bytes.Length; i++)bytes[i] = 0;for (int m = 0; m < x; m++){for (int n = 0; n < y; n++){//黑色存储障碍区域 白色存储可行走区域bytes[m * x + n] = (byte)(map[m, n] ? 255 : 0);}}bitmap.LoadRawTextureData(bytes);//创建、保存资产AssetDatabase.CreateAsset(bitmap, filePath);AssetDatabase.SaveAssets();AssetDatabase.Refresh();//选中EditorGUIUtility.PingObject(bitmap);}
}
源码以上传至SKFramework框架Package Manager中:
相关文章:

如何在Unity中实现AStar寻路算法及地图编辑器
文章目录AStar算法简介实现Node节点节点间的估价算法核心邻节点的搜索方式地图编辑器简介实现绘制地图网格障碍/可行走区域地图数据存储AStar算法 简介 Unity中提供了NavMesh导航寻路的AI功能,如果项目不涉及服务端它应该能满足大部分需求,但如果涉及服…...

线性代数之矩阵
一、思维导图二、矩阵及其运算1、矩阵的定义注:零矩阵:元素均为0 的矩阵,通常记作0m*n称为矩阵的类型。满足阶梯形矩阵 行简化的阶梯形矩阵即满足如下条件的矩阵: (1)阶梯形; (2)非零首元所在列其余元素均为0 ; (3) 非…...

【个人首测】百度文心一言 VS ChatGPT GPT-4
昨天我写了一篇文章GPT-4牛是牛,但这几天先别急,文中我测试了用GPT-4回答ChatGPT 3.5 和 Notion AI的问题,大家期待的图片输入也没有出现。 昨天下午百度发布了文心一言,对标ChatGPT,录屏无实机演示让百度股价暴跌。但是晚上百度就…...
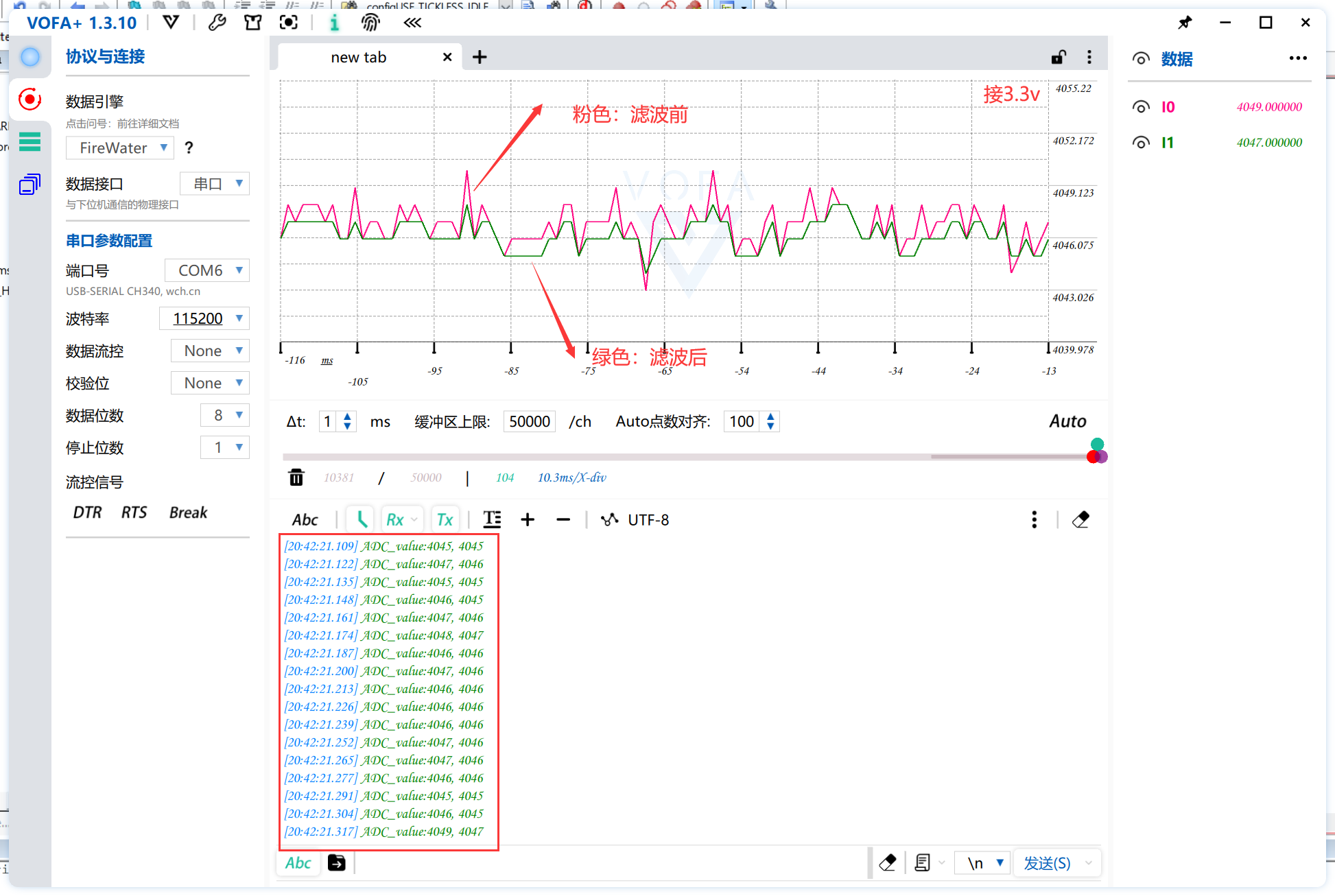
基于STM32的ADC采样及各式滤波实现(HAL库,含VOFA+教程)
前言:本文为手把手教学ADC采样及各式滤波算法的教程,本教程的MCU采用STM32F103ZET6。以HAL库的ADC采样函数为基础进行教学,通过各式常见滤波的实验结果进行分析对比,搭配VOFA工具直观的展示滤波效果。ADC与滤波算法都是嵌入式较为…...
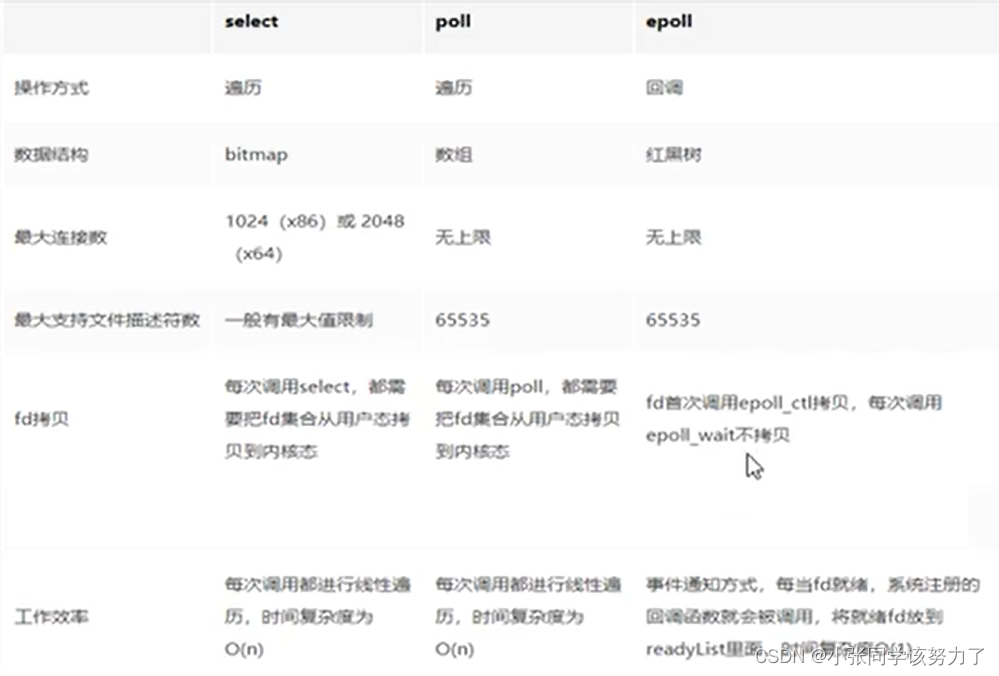
Redis高级篇
文章目录面试题库redis有哪些用法?redis单线程时代性能依然很快的原因?主线程和IO线程怎么协作完成请求处理的BigKey(重要)什么算是BigKey?怎么发现BigKey?怎么删除bigkey?bigkey生产调优缓存双…...
这句话一般是干什么的,在代码中可以不加么?)
sess.close()这句话一般是干什么的,在代码中可以不加么?
sess.close()这句话是用于关闭TensorFlow会话对象的方法。 关闭会话对象可以释放资源,避免内存泄漏,以及清除图中的变量和操作。 在代码中是否可以不加这句话,取决于你是如何创建和使用会话对象的。如果你使用了with语句来创建和管理会话对…...

网络舆情监测处置平台,TOOM舆情如何做好舆情风险点及防控措施?
网络舆情监测处置平台是一个综合性的系统,旨在帮助企业、政府或其他组织有效地管理和处置网络舆情。从多个角度来分析该平台,我们可以考虑以下几个方面: 1,技术实现 网络舆情监测处置平台的技术实现是其核心,它通常采…...
百度文心一言对标 ChatGPT,你怎么看?
文心一言 VS ChatGPT接受不完美 期待进步里程碑意义文心一言初体验✔ 文学创作✔ 商业文案创作✔ 数理逻辑推算✔ 中文理解✔ 多模态生成写在最后何为文心?“文”就是我们中华语言文字中的文,“心”是希望该语言模型可以用心的去理解语言,用心…...

阿里笔试2023-3-15
太菜了,记录一下笔试题目,代码有更好解法欢迎分享。 1、满二叉子树的数量。 给定一颗二叉树,试求这课二叉树有多少个节点满足以该节点为根的子树是满二叉树?满二叉树指每一层都达到节点最大值。 第一行输入n表示节点数量ÿ…...
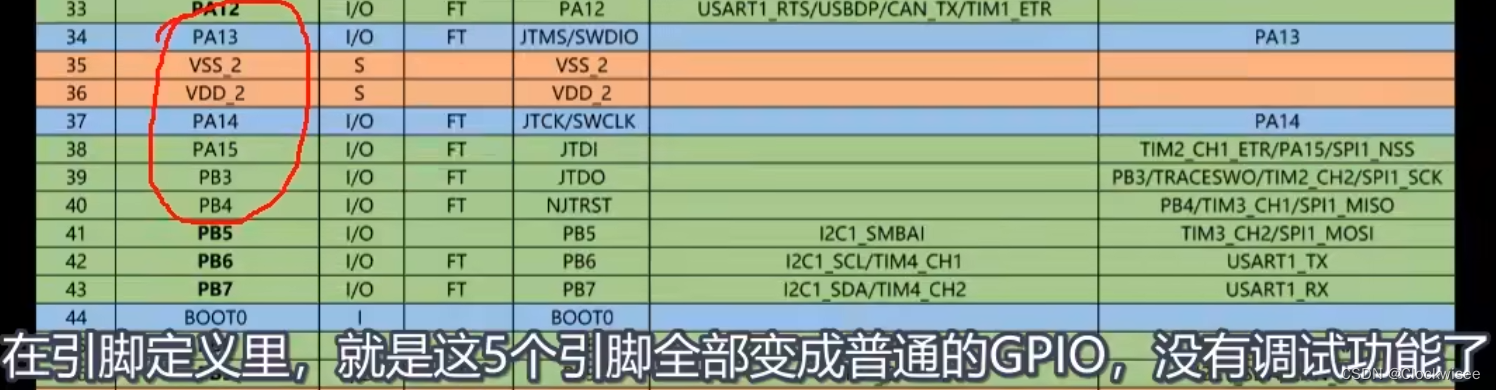
STM32:TIM定时器输出比较(OC)
一、输出比较简介 1、输出比较 OC(Output Comapre)输出比较输出比较可以通过比较CNT(时基单元)和CCR(捕获单元)寄存器值的关系,来对输出电平进行置1、置0或翻转的操作,用于输出一定频…...

HTTPS 加密协议
✏️作者:银河罐头 📋系列专栏:JavaEE 🌲“种一棵树最好的时间是十年前,其次是现在” 目录HTTPS"加密" 是什么HTTPS 的工作过程引入证书HTTPS http 安全层 (SSL) SSL 用来加密的协议,也叫 TLS …...

分布式锁和分布式事务
分布式锁 没有图形,只通过大量文字进行说明。分布式锁:redis分布式锁, zk分布式锁, 数据库做分布式锁 redis分布式锁 setnx key value ex 10 原子操作 AB两个线程减库存业务,假设库存是10 A线程获取锁,…...

RK3568平台开发系列讲解(驱动基础篇)I2C协议介绍
🚀返回专栏总目录 文章目录 一、I2C基本读写过程二、通讯的起始和停止信号三、数据有效性四、地址及数据方向五、响应沉淀、分享、成长,让自己和他人都能有所收获!😄 📢I2C的协议定义了通讯的起始和停止信号、数据有效性、响应、仲裁、时钟同步和地址广播等环节。 一、…...

HTML 音频(Audio)
HTML 音频(Audio) 声音在HTML中可以以不同的方式播放. 问题以及解决方法 在 HTML 中播放音频并不容易! 您需要谙熟大量技巧,以确保您的音频文件在所有浏览器中(Internet Explorer, Chrome, Firefox, Safari, Opera)和所有硬件上…...
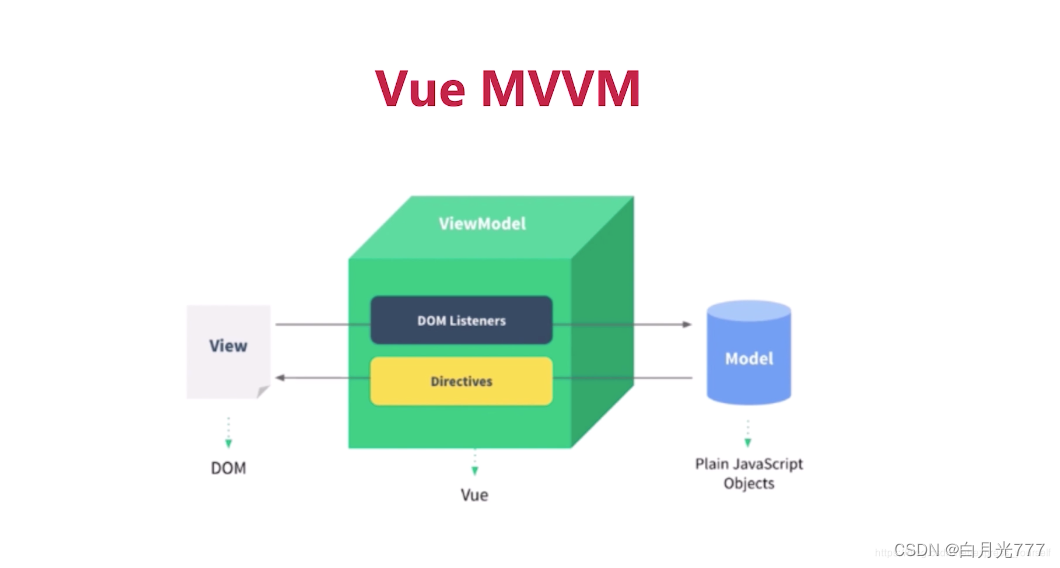
什么是Vue
✅作者简介:CSDN一位小博主,正在学习前端,欢迎大家一起来交流学习🏆 📃个人主页:白月光777的CSDN博客 🔥系列专栏:Vue从入门到进阶 💬个人格言:但行好事&…...

python 内置函数和多线程
以下是Python的一些内置函数。这些函数是Python语言提供的基本功能,可以在不需要导入任何其他模块的情况下直接使用。这些函数可以完成广泛的任务,例如数学运算,序列和集合操作,类型转换,文件操作等等。透彻理解这些函…...

【Spring】我抄袭了Spring,手写一套MySpring框架。。。
这篇博客实现了一个简单版本的Spring,主要包括Spring的Ioc和Aop功能 文章目录这篇博客实现了一个简单版本的Spring,主要包括Spring的Ioc和Aop功能🚀ComponentScan注解✈️Component注解🚁在spring中ioc容器的类是ApplicationConte…...
vue中的生命周期
前言 很多时候我们希望能在 vue 生命周期的过程中执行一些操作,生命周期钩子函数也因此诞生了。相信使用过 vue 框架的同学都知道,生命周期的钩子函数允许我们在实例的不同阶段执行各种操作,便于我们更好的控制和使用实例。 生命周期钩子函数…...
)
硬件原理图设计规范(二)
1、可编程逻辑器件 编号 级别 条目内容 备注 1 推荐 FPGA的LE资源利用率要保证在50%~80%之间,EPLD的MC资源的利用率要保证在50%~90%之间。对于FPGA中的锁相环、RAM、乘法器、DSP单元、CPU核等资源,经过精确预算,…...

复旦微ZYNQ7020全国产替代方案设计
现在国产化进度赶人,进口的芯片只做了个功能验证,马上就要换上国产的。国内现在已经做出来zynq的只有复旦微一家,已经在研制的有上海安路,还有成都华微(不排除深圳国威也在做,毕竟这个市场潜力很大…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...
