常见背包问题
一.前言
若你想学习或正在学习动态规划,背包问题一定是你需要了解的一种题型,并且大多数人最初都是从背包问题入坑进而打开动态规划这一大门。背包问题分为多种,你可以先掌握最常见的主要是三类:01背包、完全背包、多重背包
二.分析背包问题
1)01背包
在考虑一个物品时(从目标容器到物品大小容器考虑(保证只放一次)),放入当前物品后,所剩空间只能考虑其他物品
★状态:考虑了前i个物品,大小为j的容器能放入的最大价值的商品
转移方程:f[i][j]=max(f[i-1][j],f[i-1][j-V[i]])+W[i])
转移方程:dp[j]=max(dp[j-V[i]],dp[j]])(注:等号右边的dp为上个循环的结果,即考虑当前物品前面的所有物品的结果)
2)多重背包
在考虑一个物品时,将放不同个数看成不同物品,即可转化为01背包问题
3)完全背包
在考虑一个物品时(从物品大小容器到目标容器考虑(保证应放尽放)),放入当前物品后所剩空间只能考虑其他物品
三.例题
1)题目
01背包
有 n 件物品和一个容量是 v 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
代码
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int v[N]; //每个物品的体积
int w[N]; //每个物品的价值
int f[N][N]; //状态转移方程,上面有详细解释
int main(){int n,m;scanf("%d%d",&n,&m); //输入物品数量和背包容量for(int i = 1;i <= n;i ++) scanf("%d%d",&v[i],&w[i]); //输入每个物体的体积和价值for(int i = 1;i <= n;i ++){for(int j = 0;j <= m;j ++){f[i][j] = f[i - 1][j]; //合并内容if(j >= v[i]) f[i][j] = max(f[i][j],f[i - 1][j - v[i]] + w[i]); //已经把f[i][j]赋值为f[i - 1][j]了,现在就可以直接用f[i][j]了}}printf("%d",f[n][m]);return 0;
}2)题目
有 n种物品和一个容量是v的背包,每种物品都有无限件可用。
第 i 种物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
代码
#include <iostream>using namespace std;const int N = 1100;
int n, m;
int v[N], w[N];
int f[N][N];int main() {int n, m;cin >> n >> m;for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];for (int i = 1; i <= n; i ++ ) {for (int j = 1; j <= m; j ++ ) {f[i][j] = f[i - 1][j];for (int k = 1; k <= j / v[i]; k ++ ) {f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);}}}cout << f[n][m] << endl;return 0;
}3)题目
有 n 种物品和一个容量是 v 的背包。
第 i 种物品最多有 si 件,每件体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
代码
#include <iostream>
#include <algorithm>using namespace std;
const int N = 110;int v[N], w[N], s[N];
int f[N][N];
int n, m;int main(){cin >> n >> m;for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i] >> s[i];for(int i = 1; i <= n; i ++){//枚举背包for(int j = 1; j <= m; j ++){//枚举体积for(int k = 0; k <= s[i]; k ++){if(j >= k * v[i]){f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);}}}}cout << f[n][m] << endl;return 0;
}
~感谢观看❥(^_-)
相关文章:

常见背包问题
一.前言若你想学习或正在学习动态规划,背包问题一定是你需要了解的一种题型,并且大多数人最初都是从背包问题入坑进而打开动态规划这一大门。背包问题分为多种,你可以先掌握最常见的主要是三类:01背包、完全背包、多重背包二.分析…...

【python】python编译器以及安装
✅作者简介:一名在读大二学生,希望大家多多支持 🔥系列专栏:python 💬个人主页:小园园子的CSDN博客 python编译器以及安装一、编译器与解释器详细内容Python解释器种类Python的运行机制二、python环境搭建p…...

Effective C++快速复习
Effective C快速复习 习惯 C 01 视 C 为一个语言联邦:C、Object-Oriented C、Template C、STL 02 尽量以 const, enum, inline 替换 #define:其实是尽量以编译器替换预处理器比较好,因为 #define 只是简单的字符串匹配替换,编译…...

【华为OD机试真题JAVA】绘图机器的绘图问题
标题:绘图机器的绘图问题| 时间限制:1秒 | 内存限制:262144K | 语言限制:不限 绘图机器的绘图笔初始位置在原点(0,0) 机器启动后按照以下规则来进行绘制直线 1. 尝试沿着横线坐标正向绘制直线 直到给定的终点E 2. 期间可以通过指令在纵坐标轴方向进行偏移 off…...

GPT-4最震撼我的一点
昨天我看了一遍OpenAI发的视频和论文,最震撼我的并不是根据手绘草图生成HTML页面代码,因为草图太简单,对于复杂的有交互的界面,还不知道它的能力究竟如何,能不能生成准确的、清晰的代码,我再实验一下再给大…...
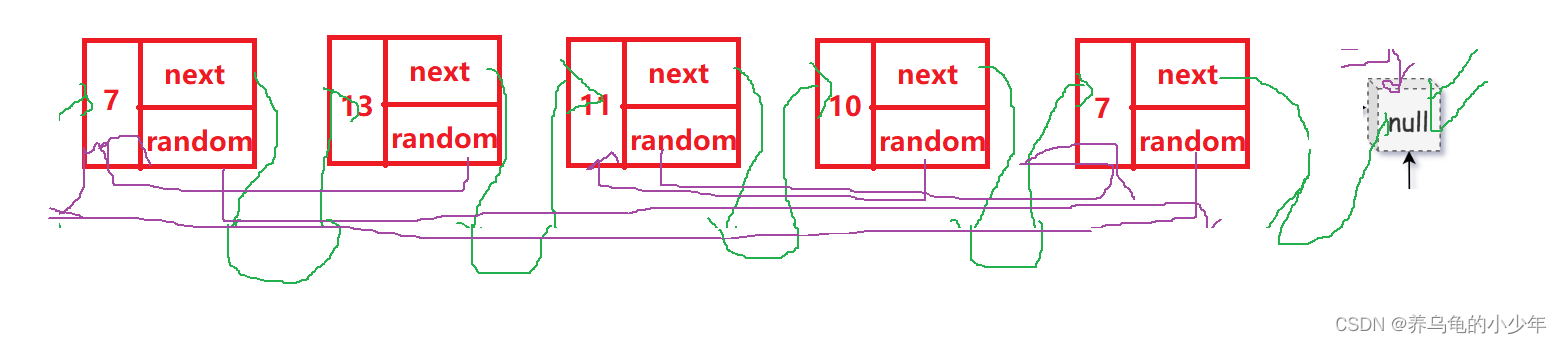
LeetCode-复制带随机指针的链表
题目描述: 给你一个长度为 n 的链表,每个节点包含一个额外增加的随机指针 random ,该指针可以指向链表中的任何节点或空节点。 构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成,其中每个新节点的值都设为其对应的…...
如何在Unity中实现AStar寻路算法及地图编辑器
文章目录AStar算法简介实现Node节点节点间的估价算法核心邻节点的搜索方式地图编辑器简介实现绘制地图网格障碍/可行走区域地图数据存储AStar算法 简介 Unity中提供了NavMesh导航寻路的AI功能,如果项目不涉及服务端它应该能满足大部分需求,但如果涉及服…...

线性代数之矩阵
一、思维导图二、矩阵及其运算1、矩阵的定义注:零矩阵:元素均为0 的矩阵,通常记作0m*n称为矩阵的类型。满足阶梯形矩阵 行简化的阶梯形矩阵即满足如下条件的矩阵: (1)阶梯形; (2)非零首元所在列其余元素均为0 ; (3) 非…...

【个人首测】百度文心一言 VS ChatGPT GPT-4
昨天我写了一篇文章GPT-4牛是牛,但这几天先别急,文中我测试了用GPT-4回答ChatGPT 3.5 和 Notion AI的问题,大家期待的图片输入也没有出现。 昨天下午百度发布了文心一言,对标ChatGPT,录屏无实机演示让百度股价暴跌。但是晚上百度就…...
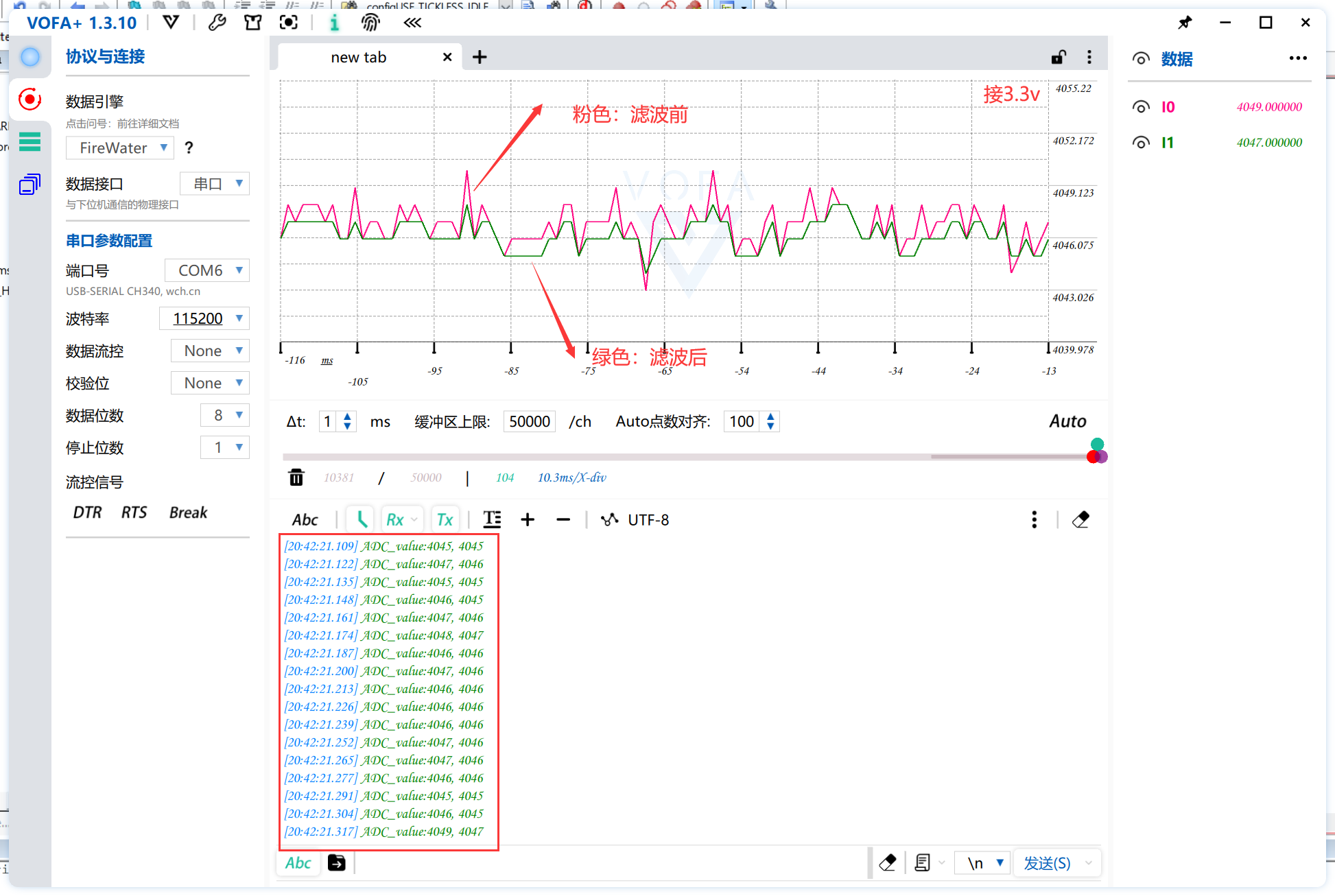
基于STM32的ADC采样及各式滤波实现(HAL库,含VOFA+教程)
前言:本文为手把手教学ADC采样及各式滤波算法的教程,本教程的MCU采用STM32F103ZET6。以HAL库的ADC采样函数为基础进行教学,通过各式常见滤波的实验结果进行分析对比,搭配VOFA工具直观的展示滤波效果。ADC与滤波算法都是嵌入式较为…...
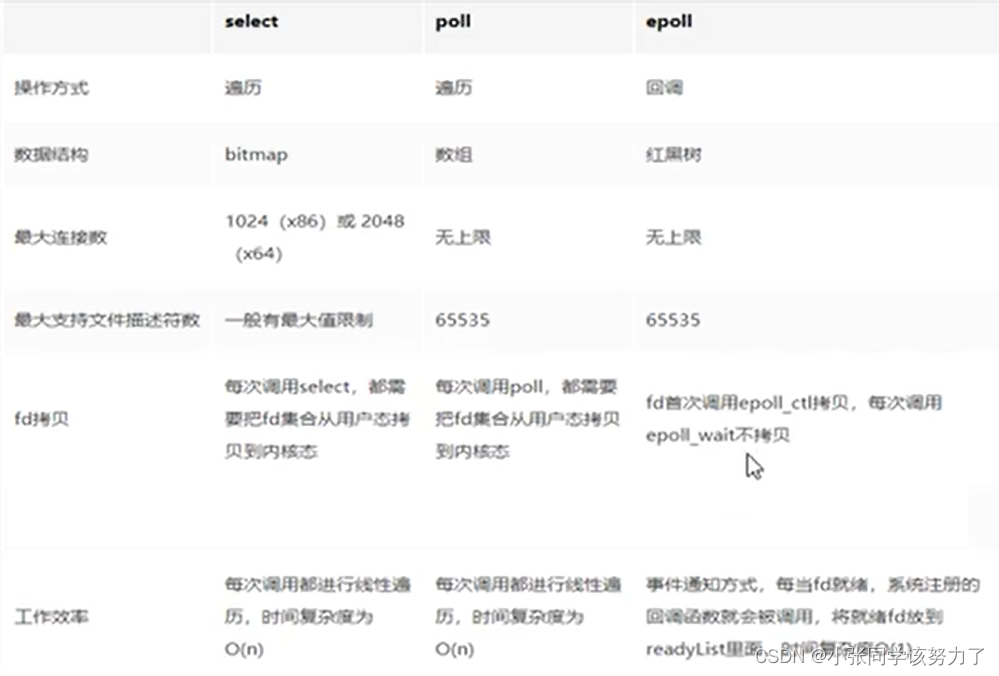
Redis高级篇
文章目录面试题库redis有哪些用法?redis单线程时代性能依然很快的原因?主线程和IO线程怎么协作完成请求处理的BigKey(重要)什么算是BigKey?怎么发现BigKey?怎么删除bigkey?bigkey生产调优缓存双…...
这句话一般是干什么的,在代码中可以不加么?)
sess.close()这句话一般是干什么的,在代码中可以不加么?
sess.close()这句话是用于关闭TensorFlow会话对象的方法。 关闭会话对象可以释放资源,避免内存泄漏,以及清除图中的变量和操作。 在代码中是否可以不加这句话,取决于你是如何创建和使用会话对象的。如果你使用了with语句来创建和管理会话对…...

网络舆情监测处置平台,TOOM舆情如何做好舆情风险点及防控措施?
网络舆情监测处置平台是一个综合性的系统,旨在帮助企业、政府或其他组织有效地管理和处置网络舆情。从多个角度来分析该平台,我们可以考虑以下几个方面: 1,技术实现 网络舆情监测处置平台的技术实现是其核心,它通常采…...
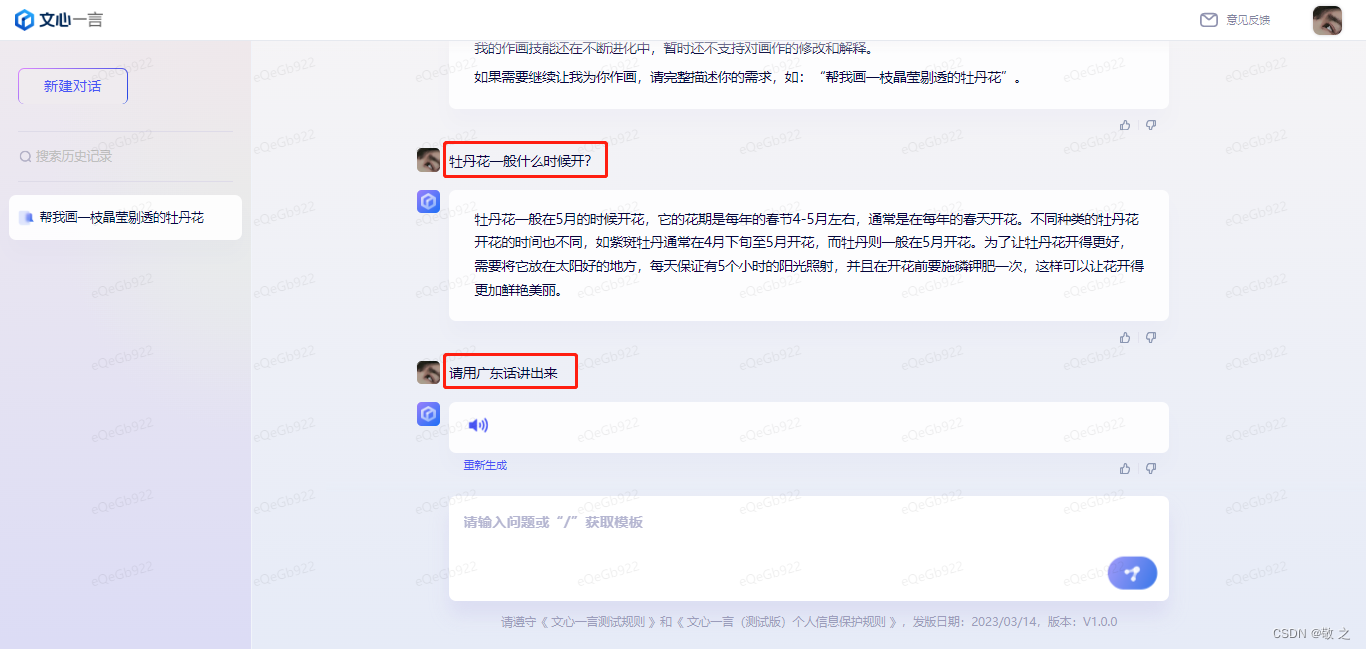
百度文心一言对标 ChatGPT,你怎么看?
文心一言 VS ChatGPT接受不完美 期待进步里程碑意义文心一言初体验✔ 文学创作✔ 商业文案创作✔ 数理逻辑推算✔ 中文理解✔ 多模态生成写在最后何为文心?“文”就是我们中华语言文字中的文,“心”是希望该语言模型可以用心的去理解语言,用心…...

阿里笔试2023-3-15
太菜了,记录一下笔试题目,代码有更好解法欢迎分享。 1、满二叉子树的数量。 给定一颗二叉树,试求这课二叉树有多少个节点满足以该节点为根的子树是满二叉树?满二叉树指每一层都达到节点最大值。 第一行输入n表示节点数量ÿ…...
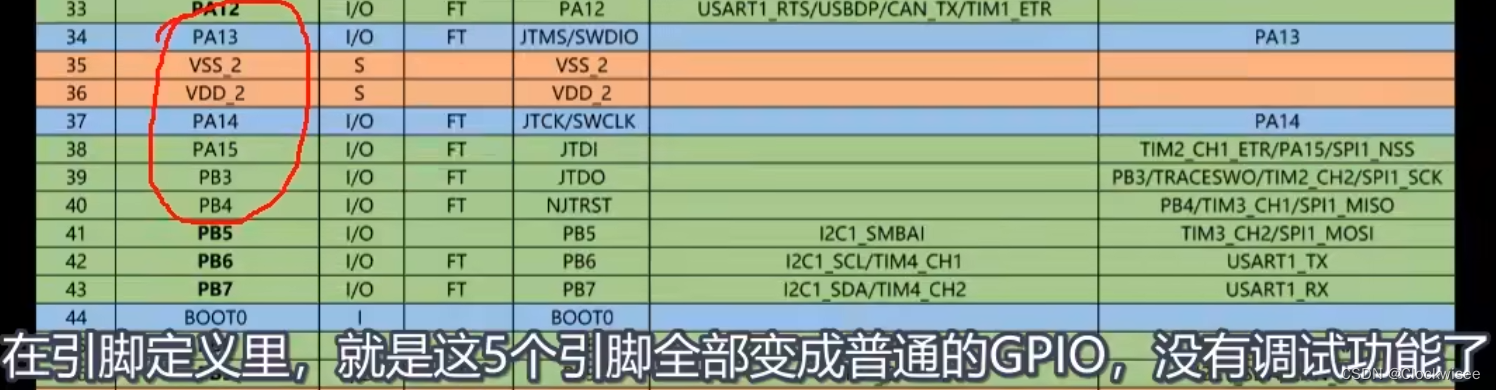
STM32:TIM定时器输出比较(OC)
一、输出比较简介 1、输出比较 OC(Output Comapre)输出比较输出比较可以通过比较CNT(时基单元)和CCR(捕获单元)寄存器值的关系,来对输出电平进行置1、置0或翻转的操作,用于输出一定频…...

HTTPS 加密协议
✏️作者:银河罐头 📋系列专栏:JavaEE 🌲“种一棵树最好的时间是十年前,其次是现在” 目录HTTPS"加密" 是什么HTTPS 的工作过程引入证书HTTPS http 安全层 (SSL) SSL 用来加密的协议,也叫 TLS …...

分布式锁和分布式事务
分布式锁 没有图形,只通过大量文字进行说明。分布式锁:redis分布式锁, zk分布式锁, 数据库做分布式锁 redis分布式锁 setnx key value ex 10 原子操作 AB两个线程减库存业务,假设库存是10 A线程获取锁,…...

RK3568平台开发系列讲解(驱动基础篇)I2C协议介绍
🚀返回专栏总目录 文章目录 一、I2C基本读写过程二、通讯的起始和停止信号三、数据有效性四、地址及数据方向五、响应沉淀、分享、成长,让自己和他人都能有所收获!😄 📢I2C的协议定义了通讯的起始和停止信号、数据有效性、响应、仲裁、时钟同步和地址广播等环节。 一、…...

HTML 音频(Audio)
HTML 音频(Audio) 声音在HTML中可以以不同的方式播放. 问题以及解决方法 在 HTML 中播放音频并不容易! 您需要谙熟大量技巧,以确保您的音频文件在所有浏览器中(Internet Explorer, Chrome, Firefox, Safari, Opera)和所有硬件上…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...
