week13周报
一.动态规划
走楼梯2
难点:不能连续走三次两级台阶如何表示
思路:可以用二维数组f[i][j],i表示当前台阶数,j表示已经连续走了j次二级台阶了
转移方程:f[i+2][j+1]=f[i+2][j+1]+f[i][j] 当j!=2时,我们可以选择走二级台阶
f[i+1][0]=f[i+1][0]+f[i][j] 选择走一级台阶,此时j变为了0
这两种情况是同时进行的
代码:
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n;
cin>>n;
long long f[55][5];
memset(f,0,sizeof(f));
f[0][0]=1;
for(int i=0;i<=n;i=i+1)
{
for(int j=0;j<=2;j=j+1)
{
if(j!=2)
{
f[i+2][j+1]=f[i+2][j+1]+f[i][j];
}
f[i+1][0]=f[i+1][0]+f[i][j];
}
}
long long sum=f[n][0]+f[n][1]+f[n][2];
cout<<sum;
return 0;
}
2.任务分配
难点:是以时刻来枚举还是任务编号来枚举
思路:本题以时刻来枚举,可以通过起始时间和结束时间来进行转移
转移方程:
f[g[num].e]=max(f[g[num].e],f[i]+g[num].w);当此时刻i与当前任务的起始时间相等时,我们可以选择做此任务
f[i+1]=max(f[i],f[i+1]);此时刻不选择做任务或者无任务可做
两个方程同时进行
代码:
#include <bits/stdc++.h>
using namespace std;
struct ren
{
int s;
int e;
int w;
}g[1005];
bool cmp (ren a,ren b)
{
return (a.s<b.s||a.s==b.s&&a.e<b.e);
}
int f[1006];
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i=i+1)
{
cin>>g[i].s>>g[i].e>>g[i].w;
}
sort(g+1,g+n+1,cmp);
int num=1;
for(int i=1;i<=1005;i=i+1)
{
while(i==g[num].s)
{
f[g[num].e]=max(f[g[num].e],f[i]+g[num].w);
num=num+1;
}
f[i+1]=max(f[i],f[i+1]);
}
cout<<f[1005];
}
3.走路(此题略过,思路和前面两题类似)
二.二分查找
1.饿饿 饭饭
难点:如何分辨题目为二分答案类型题
思路:由于此题数据极大,普通的枚举一定过不了,需要一个快速的方法把前面的绝大部分流程跳过,因此我们用到了二分答案
二分答案的操作:寻找打到了mid轮之后,再打一轮就会超过总数k。判断条件:第mid轮打的total份饭<=总数k
代码:
#include <bits/stdc++.h>
using namespace std;
long long a[100050],c[100050];
int n;
long long k;
long long check(int x)
{
long long tt=0;
for(int i=1;i<=n;i=i+1)
{
if(a[i]<=x)
{
tt=tt+a[i];
}
else
{
tt=tt+x;
}
}
return tt;
}
int main()
{
cin>>n>>k;
long long zong=0;
for(int i=1;i<=n;i=i+1)
{
cin>>a[i];
zong=zong+a[i];
}
if(zong<k)
{
cout<<"-1";
}
else if(zong==k)
{
return 0;
}
else
{
int l=0;
int r=1e9;
while(l+1<r)
{
int mid=(l+r)/2;
if(check(mid)>k)
{
r=mid;
}
else
{
l=mid;
}
}
k=k-check(l);
int tot=0;
for(int i=1;i<=n;i=i+1)
{
if(a[i]>l)
{
c[++tot]=i;
}
}
for(int i=k+1;i<=tot;i=i+1)
{
cout<<c[i]<<" ";
}
for(int i=1;i<=k;i=i+1)
{
if(a[c[i]]!=l+1)
{
cout<<c[i]<<" ";
}
}
}
}
三.set的用法
1.订单编号
知识点:set容器其中的元素会自动排好队,并且不允许有重复元素
set的各常用成员函数列表:
insert()–在集合中插入元素
begin()–返回指向第一个元素的迭代器
end()–返回指向最后一个元素下一个位置(注意不是最后一个元素)的迭代器
clear()–清除所有元素
count()–返回某个值元素的个数
empty()–如果集合为空,返回true
find()–返回一个指向被查找到元素的迭代器
size()–集合中元素的数目
swap()–交换两个集合变量
upper_bound()–返回大于某个值元素的迭代器
lower_bound()--饭后第一个大于某个值元素的元素位置
max_size()–返回集合能容纳的元素的最大限值
rbegin()–返回指向集合中最后一个元素的反向迭代器
rend()–返回指向集合中第一个元素的反向迭代器
erase(itr)-删除整个已存在的容器
难点:此题需要返回未出现过的比原先值大的第一个数,这需要枚举很多内容,极有可能出现time limited这一错误信息
思路:set函数中的lower_bound()函数可以直接返回第一个大于元素的位置,可以用set存储
另外,我们可以用分区间的做法,来把已选值剔除出我们的枚举区间
另另外,这题思路好难,我尽力了
代码:
#include <bits/stdc++.h>
using namespace std;
int n;
set<pair<int,int> > c;
inline void insert(int l,int r)//往insert()函数中内置代码
{
if(l>r)
{
return;
}
c.insert(make_pair(r,l));
}
int main()
{
cin>>n;
c.insert(make_pair(2e9,1));
for(int i=1;i<=n;i=i+1)
{
int x;
cin>>x;
auto itr=c.lower_bound(make_pair(x,0));
if(itr->second<=x)//分区间做法
{
cout<<x<<" ";
insert(itr->second,x-1);
insert(x+1,itr->first);
c.erase(itr);
}
else
{
cout<<itr->second<<" ";
insert(itr->second+1,itr->first);
c.erase(itr);
}
}
}
相关文章:

week13周报
一.动态规划走楼梯2难点:不能连续走三次两级台阶如何表示思路:可以用二维数组f[i][j],i表示当前台阶数,j表示已经连续走了j次二级台阶了转移方程:f[i2][j1]f[i2][j1]f[i][j] 当j!2时,我们可以选择走二级台阶…...

离散选择模型中的分散系数theta到底该放在哪里呢?
前言 \quad~~一直都在想为啥子离散选择模型中分散系数以分母形式出现而在路径选择公式中以系数形式出现呢?看着公式想了想,现在想出了一个似乎感觉应该差不多很合理的答案,希望与大家一起探讨。 进入正题 根据随机效用理论,决策…...

【CSAPP】进程 | 上下文切换 | 用户视角下的并发进程
💭 写在前面:本文将学习《深入理解计算机系统》的第六章 - 关于异常控制流和系统级 I/O 的 进程部分。CSAPP 是计算机科学经典教材《Computer Systems: A Programmers Perspective》的缩写,该教材由Randal E. Bryant和David R. OHallaron 合著…...
节流还在用JS吗?CSS也可以实现哦
函数节流是一个我们在项目开发中常用的优化手段,可以有效避免函数过于频繁的执行。一般函数节流用在scroll页面滚动,鼠标移动等。 为什么需要节流呢,因为触发一次事件就会执行一次事件,这样就形成了大量操作dom,会出现卡顿的情况…...

带你看看 TypeScript 5.0 的新特性
一、写在前面 TypeScript 5.0 已经于 2023 年 3 月 16 日发布了,带来了许多新功能,同时也在性能方面进行了优化,下面让我们来一起看看新版 TypeScript 中比较有重要的变化吧。 二、新特性 2-1、速度、包体积优化 首先是新版本性能的提升&…...

C语言预处理条件语句的 与或运算
C语言预处理条件语句的 与或运算 1.#ifdef 与或运算 #ifdef (MIN) && (MAX) ----------------------------错误使用 #if defined(MIN) && defined(MAX) ---------------- 正确使用 #ifdef (MIN) || (MAX) -----------------------------错误使用 …...
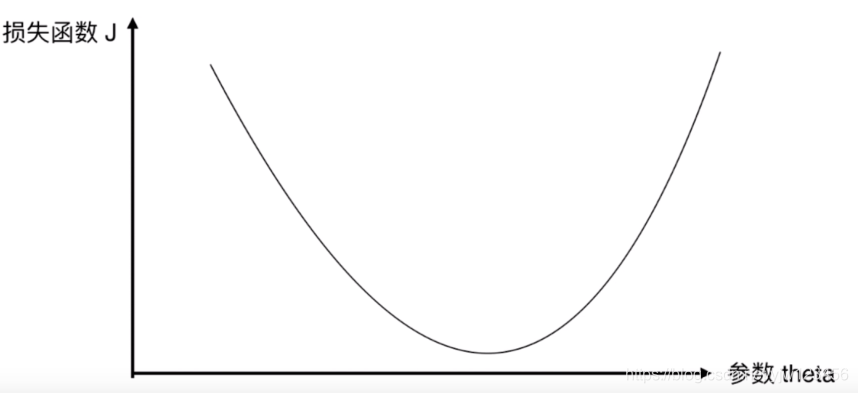
从零实现深度学习框架——学习率调整策略介绍
引言 本着“凡我不能创造的,我就不能理解”的思想,本系列文章会基于纯Python以及NumPy从零创建自己的深度学习框架,该框架类似PyTorch能实现自动求导。 要深入理解深度学习,从零开始创建的经验非常重要,从自己可以理解的角度出发,尽量不使用外部完备的框架前提下,实现我…...
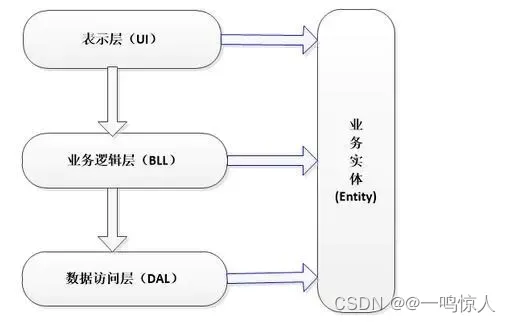
系统架构:经典三层架构
引言 经典三层架构是分层架构中最原始最典型的分层模式,其他分层架构都是其变种或扩展,例如阿里的四层架构模式和DDD领域驱动模型。阿里的 四层架构模型在三层基础上增加了 Manager 层,从而形成变种四层模型;DDD架构则在顶层用户…...
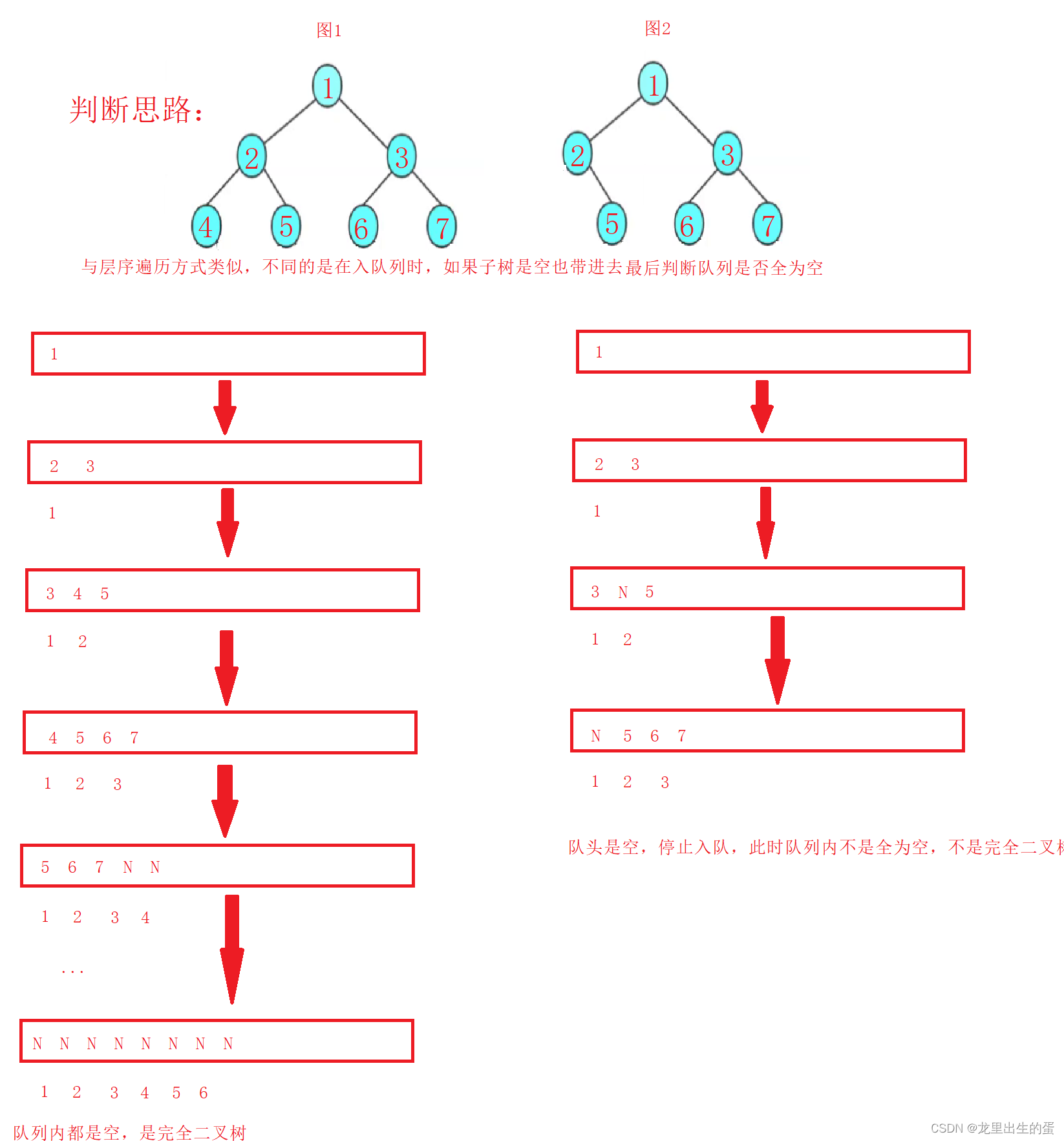
数据结构--二叉树
目录1.树概念及结构1.1数的概念1.2数的表示2.二叉树概念及结构2.1二叉树的概念2.2数据结构中的二叉树2.3特殊的二叉树2.4二叉树的存储结构2.4.1顺序存储2.4.2链式存储2.5二叉树的性质3.堆的概念及结构3.1堆的实现3.1.1堆的创建3.1.2堆的插入3.1.3堆顶的删除3.1.4堆的代码实现3.…...

Keil5安装和使用小记
随着keil版本的更新,一些使用问题一随之产生。本文针对安装目前最新版本keil软件和使用问题做一些总结。 目录1 Keil5下载&安装1.1 官网下载链接1.2 软件安装1.2.1 安装说明1.2.2 关于 51 和 ARM 共存的问题1.3 软件破解2 pack包安装 & 破解2.1 下载2.2 安装…...
多机器人集群网络通信协议分析
本文讨论的是多机器人网络通信各层的情况和协议。 每个机器人连接一个数据传输通信模块(以下简称为数传,也泛指市面上的图传或图数一体的通信模块),数传之间进行组网来传递信息。 根据ISO的划分,网络通信的OSI模型分…...

【PyTorch】手把手带你快速搭建PyTorch神经网络
手把手带你快速搭建PyTorch神经网络1. 定义一个Class2. 使用上面定义的Class3. 执行正向传播过程4. 总结顺序相关资料话不多说,直接上代码1. 定义一个Class 如果要做一个神经网络模型,首先要定义一个Class,继承nn.Module,也就是i…...

【完整代码】用HTML/CSS制作一个美观的个人简介网页
【完整代码】用HTML/CSS制作一个美观的个人简介网页整体结构完整代码用HTML/CSS制作一个美观的个人简介网页——学习周记1HELLO!大家好,由于《用HTML/CSS制作一个美观的个人简介网页》这篇笔记有幸被很多伙伴关注,于是特意去找了之前写的完整…...

Java分布式事务(九)
文章目录🔥XA强一致性分布式事务实战_Atomikos介绍🔥XA强一致性分布式事务实战_业务说明🔥XA强一致性分布式事务实战_项目搭建🔥XA强一致性分布式事务实战_多数据源实现🔥XA强一致性分布式事务实战_业务层实现…...
基于深度学习的动物识别系统(YOLOv5清新界面版,Python代码)
摘要:动物识别系统用于识别和统计常见动物数量,通过深度学习技术检测日常几种动物图像识别,支持图片、视频和摄像头画面等形式。在介绍算法原理的同时,给出Python的实现代码、训练数据集以及PyQt的UI界面。动物识别系统主要用于常…...

K8S集群之-ETCD集群监控
### 生产ETCD集群监控核心指标 etcd服务存活状态 up{job~"kubernetes-etcd.*"}0 说明:up0代表服务挂掉 etcd是否有脱离情况 etcd_server_has_leader{job~"kubernetes-etcd.*"}0 说明:每个instance,该值应该都…...
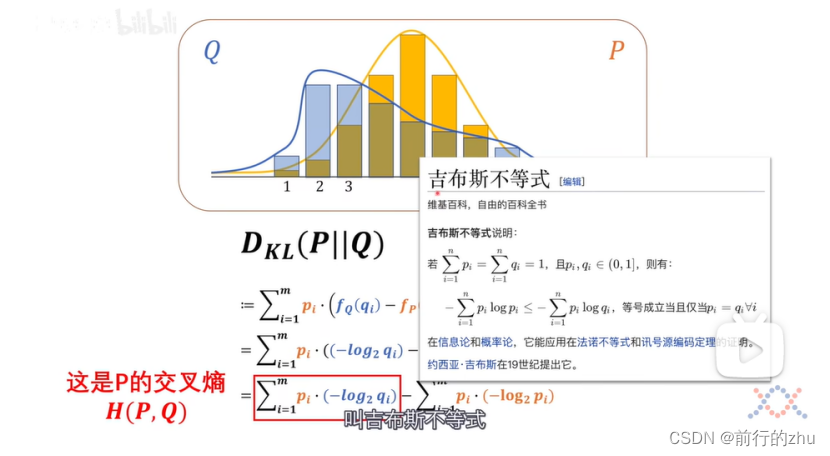
一文弄懂熵、交叉熵和kl散度(相对熵)
一个系统中事件发生的概率越大,也就是其确定性越大,则其包含的信息量越少,可以认为一个事件的信息量就是该事件发生难度的度量,事件所包含的信息量越大则其发生的难度越大。并且相互独立的事件,信息量具有可加性。相互…...
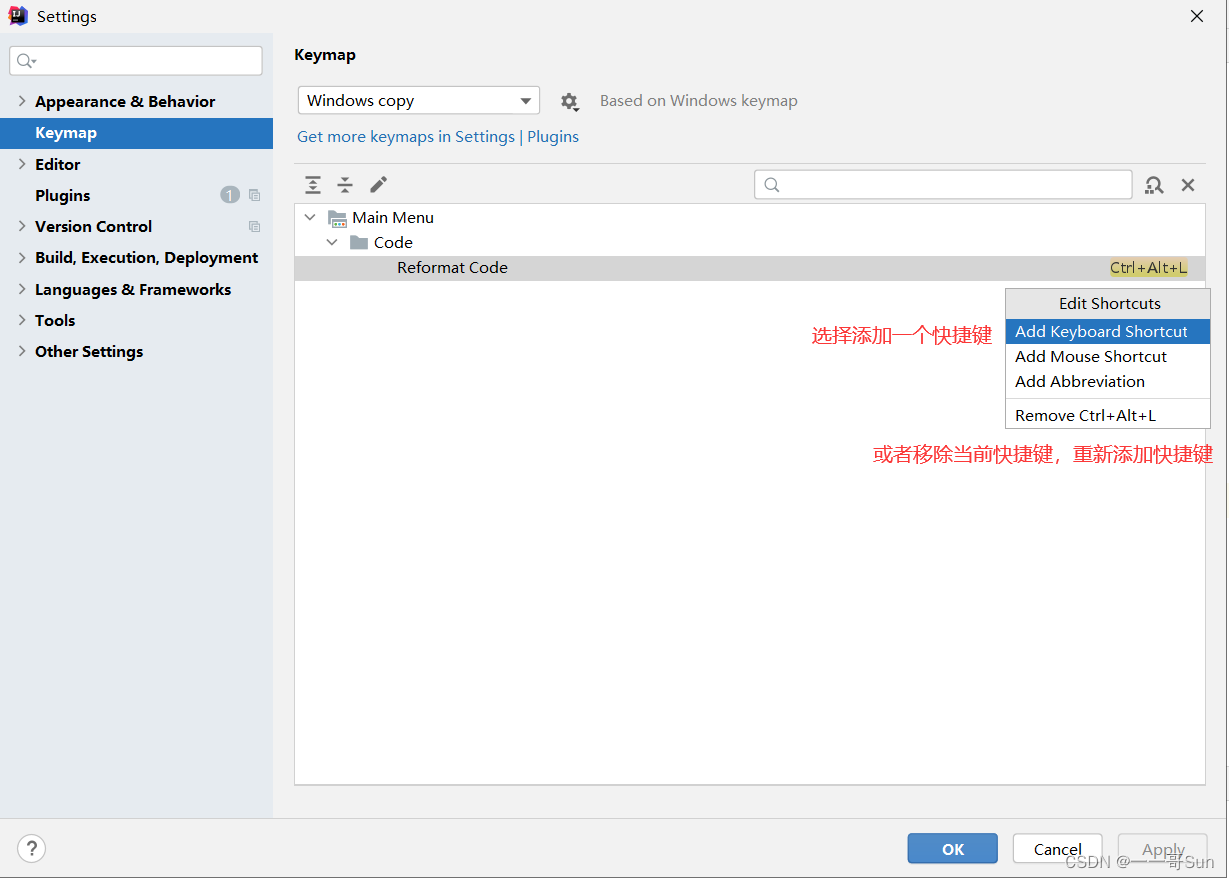
10从零开始学Java之开发Java必备软件Intellij idea的安装配置与使用
作者:孙玉昌,昵称【一一哥】,另外【壹壹哥】也是我哦CSDN博客专家、万粉博主、阿里云专家博主、掘金优质作者前言壹哥在前面的文章中,带大家下载、安装、配置了Eclipse这个更好用的IDE开发工具,并教会了大家如何在Ecli…...

04 - 进程参数编程
---- 整理自狄泰软件唐佐林老师课程 查看所有文章链接:(更新中)Linux系统编程训练营 - 目录 文章目录1. 问题1.1 再论execve(...)1.2 main函数(默认进程入口)1.3 进程空间概要图1.4 编程实验:进程参数剖析1…...

【python进阶】你真的懂元组吗?不仅是“不可变的列表”
📚引言 🙋♂️作者简介:生鱼同学,大数据科学与技术专业硕士在读👨🎓,曾获得华为杯数学建模国家二等奖🏆,MathorCup 数学建模竞赛国家二等奖🏅,…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...
