离散选择模型中的分散系数theta到底该放在哪里呢?
前言
\quad~~ 一直都在想为啥子离散选择模型中分散系数以分母形式出现而在路径选择公式中以系数形式出现呢?看着公式想了想,现在想出了一个似乎感觉应该差不多很合理的答案,希望与大家一起探讨。
进入正题
根据随机效用理论,决策者在面对 nnn 个备选方案做选择时,会根据自身的意愿感知哪一个备选方案对自身而言是最好的,从而作出自身选择。这里的最好用数量来进行衡量就可以说是效用最高的
比如从A点到B点共有 nnn 条路,我现在需要从A点到B点,从节约时间的角度来考虑的话,那么我肯定希望选择最快捷的一条路。即如果我能以最快的时间到达我的目的地的话,对我而言,我就得到了最高的出行效用。
通常呢,我们的感知能力是有限的,如果我们记选择任意一个方案 jjj 的效用为 UjU_jUj,那么 UjU_jUj 为一个随机变量,它可以分为两部分,一部分呢是我们可以以实际那数字量化出来的,我们称为系统效用。另一部分呢为我们无法测量出来的,或估测时的误差,为一个随机变量,我们称为感知误差项。因此这里的方案 jjj 的效用 UjU_jUj 就可以写为系统效用 VjV_jVj 与随机误差项 εj\varepsilon_jεj 的和,即:
Uj=Vj+εj.(1)U_j=V_j+\varepsilon_j.\tag{1}Uj=Vj+εj.(1)
在多项式Logit模型中,我们假设随机误差项 εj\varepsilon_jεj 服从零均值的Gumbel分布,其概率密度函数与累积分布函数分别为:
f(x)=1θexp(−xθ−Φ)exp[−exp(xθ−Φ)],(2)f(x)=\frac{1}{\theta}exp(-\frac{x}{\theta}-\Phi)exp[-exp(\frac{x}{\theta}-\Phi)],\tag{2}f(x)=θ1exp(−θx−Φ)exp[−exp(θx−Φ)],(2)F(x)=Pr(εj≤x)=exp[−exp(xθ−Φ)],(3)F(x)=Pr(\varepsilon_j\leq x)=exp[-exp(\frac{x}{\theta}-\Phi)],\tag{3}F(x)=Pr(εj≤x)=exp[−exp(θx−Φ)],(3)这里的参数 Φ\PhiΦ 为欧拉常数,Φ≈0.577\Phi\approx0.577Φ≈0.577。
从而可以得出决策者选择备选方案 jjj 的概率为:pj=Pr(Uj>Uk,∀k≠j)=exp(Vj/θ)∑kexp(Vk/θ).(4)p_j=Pr(U_j>U_k,\forall k\neq j)=\frac{exp(V_j/\theta)}{\sum_k exp(V_k/\theta)}.\tag{4}pj=Pr(Uj>Uk,∀k=j)=∑kexp(Vk/θ)exp(Vj/θ).(4)
而通常在路径选择情形中我们以出行阻抗作为我们的出行负效用(因为我们出行就会花费时间,金钱等,这都属于是对我们自身资源的一种消耗),负效用越小的路径被选择的可能性就会越大。这里呢,同样因为人们的感知,计算等能力有限,我们所判定的出行负效用也为一个随机变量,为可直接估量的系统效用与随机误差项的和。同样以路径 jjj 为例,其感知出行负效用为 CjC_jCj, 可进行估测的系统效用为 cjc_jcj,随机误差项为 ξj\xi_jξj, 则 CjC_jCj 就可写为:
Cj=cj+ξj,(5)C_j=c_j+\xi_j,\tag{5}Cj=cj+ξj,(5)那么选择路径 jjj 的效用就可以写为:Uj=−Cj,(6)U_j=-C_j,\tag{6}Uj=−Cj,(6)那么我们使用概率密度函数公式 (2) 计算得出的选择路径 jjj 的概率为:
pj=Pr(Uj>Uk,∀k≠j)=exp(−cj/θ)∑kexp(−ck/θ).(7)p_j=Pr(U_j>U_k,\forall k\neq j)=\frac{exp(-c_j/\theta)}{\sum_k exp(-c_k/\theta)}.\tag{7}pj=Pr(Uj>Uk,∀k=j)=∑kexp(−ck/θ)exp(−cj/θ).(7)但通常呢,路径选择概率会写为如下形式:
pj=Pr(Uj>Uk,∀k≠j)=exp(−θcj)∑kexp(−θck).(8)p_j=Pr(U_j>U_k,\forall k\neq j)=\frac{exp(-\theta c_j)}{\sum_k exp(-\theta c_k)}.\tag{8}pj=Pr(Uj>Uk,∀k=j)=∑kexp(−θck)exp(−θcj).(8)所以公式 (7) 和 (8) 同样是路径选择概率公式为什么不一样呢?
解决问题
观察概率密度函数,即公式 (2), 如果令 y=−xθy=-\frac{x}{\theta}y=−θx, 那么就有f(−θy)=1θexp(y−Φ)exp[−exp(y−Φ)],(9)f(-\theta y)=\frac{1}{\theta}exp(y-\Phi)exp[-exp(y-\Phi)],\tag{9}f(−θy)=θ1exp(y−Φ)exp[−exp(y−Φ)],(9)那么θf(−θy)=exp(y−Φ)exp[−exp(y−Φ)],(10)\theta f(-\theta y)=exp(y-\Phi)exp[-exp(y-\Phi)],\tag{10}θf(−θy)=exp(y−Φ)exp[−exp(y−Φ)],(10)对应的累积分布函数为θF(−θy)=exp[−exp(y−Φ)],(11)\theta F(-\theta y)=exp[-exp(y-\Phi)],\tag{11}θF(−θy)=exp[−exp(y−Φ)],(11)看着公式 (10) 和公式 (11) 是不是相对于(2),(3) 来说更简洁呢?公式 (10) 和公式 (11) 变成了零均值的标准Gumbel分布。所以如果公式(2)为随机变量 εj\varepsilon_jεj 的概率密度函数,从简化的角度来看,我们是不是可以让随机变量 ξj=−εj/θ\xi_j =- \varepsilon_j/\thetaξj=−εj/θ,即εj=−θξj\varepsilon_j= -\theta \xi_jεj=−θξj,那么为了统一公式 (6),我们可以令 Vj=−θcjV_j = -\theta c_jVj=−θcj,那么 εj\varepsilon_jεj 经过处理后的概率密度函数就可以表示为公式 (10) 和公式 (11),即选择路径 jjj 的概率就表示为pj=∫−∞+∞exp[−exp(εj+Vj−Vk−Φ)]∗exp(εj−Φ)exp[−exp(εj−Φ)]dεj,(12)p_j=\int_{-\infty}^{+\infty}exp[-exp(\varepsilon_j+V_j-V_k-\Phi)]* \\ exp(\varepsilon_j-\Phi)exp[-exp(\varepsilon_j-\Phi)]d\varepsilon_j, \tag{12}pj=∫−∞+∞exp[−exp(εj+Vj−Vk−Φ)]∗exp(εj−Φ)exp[−exp(εj−Φ)]dεj,(12)
整理可得概率公式为:pj=Pr(Uj>Uk,∀k≠j)=exp(Vj)∑kexp(Vk),(13)p_j=Pr(U_j>U_k,\forall k\neq j)=\frac{exp(V_j)}{\sum_k exp(V_k)},\tag{13}pj=Pr(Uj>Uk,∀k=j)=∑kexp(Vk)exp(Vj),(13)将 Vj=−θcjV_j = -\theta c_jVj=−θcj代入公式 (13),即得到公式 (8)。
相关文章:

离散选择模型中的分散系数theta到底该放在哪里呢?
前言 \quad~~一直都在想为啥子离散选择模型中分散系数以分母形式出现而在路径选择公式中以系数形式出现呢?看着公式想了想,现在想出了一个似乎感觉应该差不多很合理的答案,希望与大家一起探讨。 进入正题 根据随机效用理论,决策…...

【CSAPP】进程 | 上下文切换 | 用户视角下的并发进程
💭 写在前面:本文将学习《深入理解计算机系统》的第六章 - 关于异常控制流和系统级 I/O 的 进程部分。CSAPP 是计算机科学经典教材《Computer Systems: A Programmers Perspective》的缩写,该教材由Randal E. Bryant和David R. OHallaron 合著…...
节流还在用JS吗?CSS也可以实现哦
函数节流是一个我们在项目开发中常用的优化手段,可以有效避免函数过于频繁的执行。一般函数节流用在scroll页面滚动,鼠标移动等。 为什么需要节流呢,因为触发一次事件就会执行一次事件,这样就形成了大量操作dom,会出现卡顿的情况…...

带你看看 TypeScript 5.0 的新特性
一、写在前面 TypeScript 5.0 已经于 2023 年 3 月 16 日发布了,带来了许多新功能,同时也在性能方面进行了优化,下面让我们来一起看看新版 TypeScript 中比较有重要的变化吧。 二、新特性 2-1、速度、包体积优化 首先是新版本性能的提升&…...

C语言预处理条件语句的 与或运算
C语言预处理条件语句的 与或运算 1.#ifdef 与或运算 #ifdef (MIN) && (MAX) ----------------------------错误使用 #if defined(MIN) && defined(MAX) ---------------- 正确使用 #ifdef (MIN) || (MAX) -----------------------------错误使用 …...
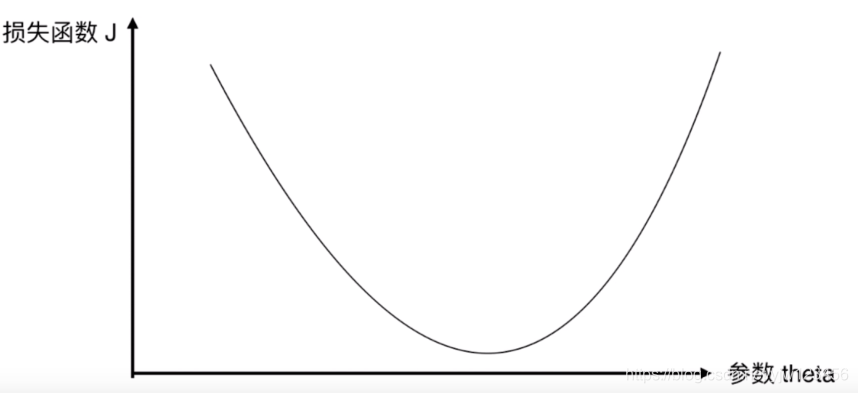
从零实现深度学习框架——学习率调整策略介绍
引言 本着“凡我不能创造的,我就不能理解”的思想,本系列文章会基于纯Python以及NumPy从零创建自己的深度学习框架,该框架类似PyTorch能实现自动求导。 要深入理解深度学习,从零开始创建的经验非常重要,从自己可以理解的角度出发,尽量不使用外部完备的框架前提下,实现我…...
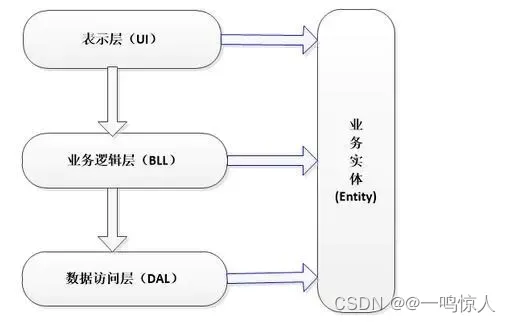
系统架构:经典三层架构
引言 经典三层架构是分层架构中最原始最典型的分层模式,其他分层架构都是其变种或扩展,例如阿里的四层架构模式和DDD领域驱动模型。阿里的 四层架构模型在三层基础上增加了 Manager 层,从而形成变种四层模型;DDD架构则在顶层用户…...
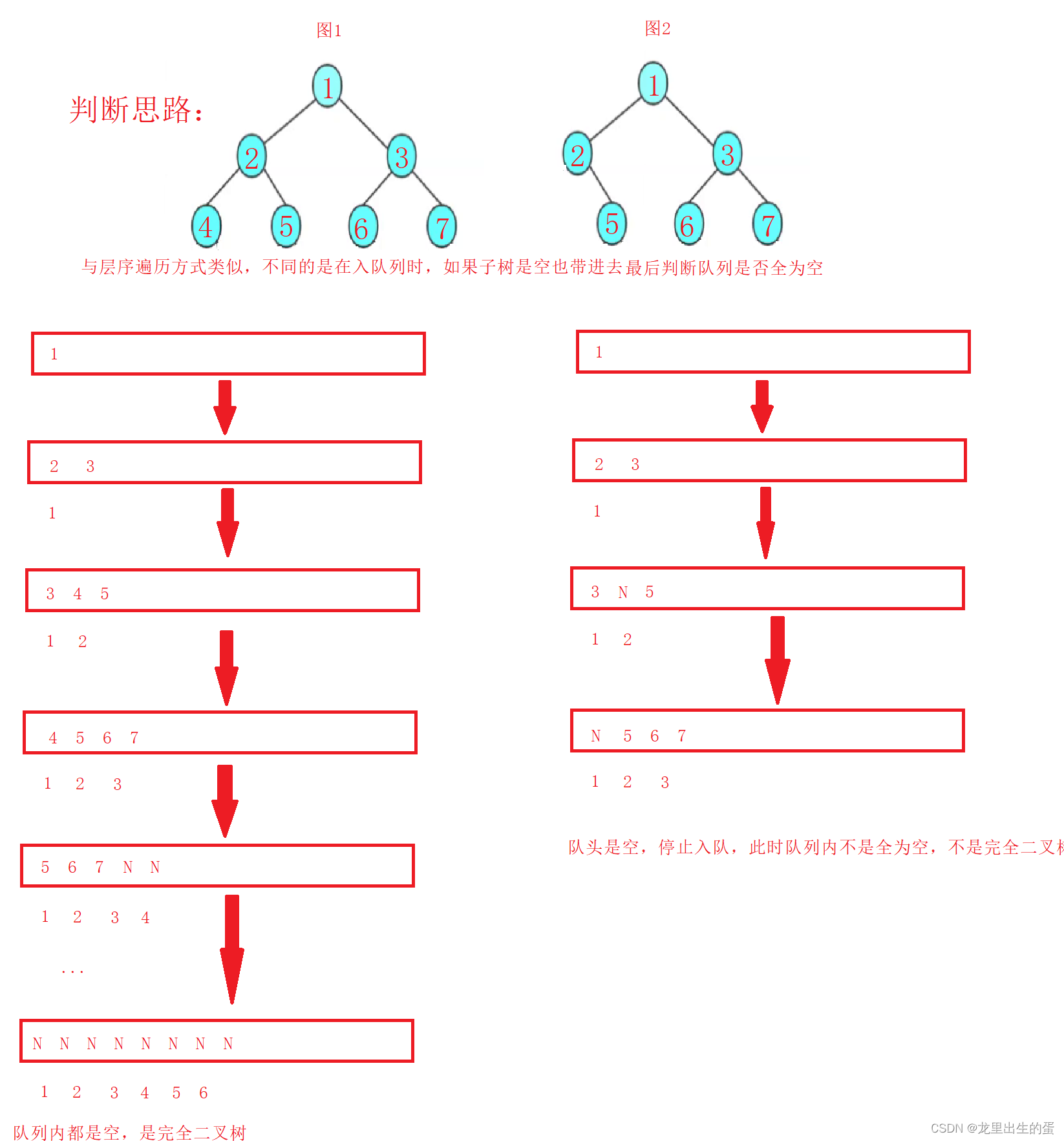
数据结构--二叉树
目录1.树概念及结构1.1数的概念1.2数的表示2.二叉树概念及结构2.1二叉树的概念2.2数据结构中的二叉树2.3特殊的二叉树2.4二叉树的存储结构2.4.1顺序存储2.4.2链式存储2.5二叉树的性质3.堆的概念及结构3.1堆的实现3.1.1堆的创建3.1.2堆的插入3.1.3堆顶的删除3.1.4堆的代码实现3.…...

Keil5安装和使用小记
随着keil版本的更新,一些使用问题一随之产生。本文针对安装目前最新版本keil软件和使用问题做一些总结。 目录1 Keil5下载&安装1.1 官网下载链接1.2 软件安装1.2.1 安装说明1.2.2 关于 51 和 ARM 共存的问题1.3 软件破解2 pack包安装 & 破解2.1 下载2.2 安装…...
多机器人集群网络通信协议分析
本文讨论的是多机器人网络通信各层的情况和协议。 每个机器人连接一个数据传输通信模块(以下简称为数传,也泛指市面上的图传或图数一体的通信模块),数传之间进行组网来传递信息。 根据ISO的划分,网络通信的OSI模型分…...

【PyTorch】手把手带你快速搭建PyTorch神经网络
手把手带你快速搭建PyTorch神经网络1. 定义一个Class2. 使用上面定义的Class3. 执行正向传播过程4. 总结顺序相关资料话不多说,直接上代码1. 定义一个Class 如果要做一个神经网络模型,首先要定义一个Class,继承nn.Module,也就是i…...

【完整代码】用HTML/CSS制作一个美观的个人简介网页
【完整代码】用HTML/CSS制作一个美观的个人简介网页整体结构完整代码用HTML/CSS制作一个美观的个人简介网页——学习周记1HELLO!大家好,由于《用HTML/CSS制作一个美观的个人简介网页》这篇笔记有幸被很多伙伴关注,于是特意去找了之前写的完整…...

Java分布式事务(九)
文章目录🔥XA强一致性分布式事务实战_Atomikos介绍🔥XA强一致性分布式事务实战_业务说明🔥XA强一致性分布式事务实战_项目搭建🔥XA强一致性分布式事务实战_多数据源实现🔥XA强一致性分布式事务实战_业务层实现…...
基于深度学习的动物识别系统(YOLOv5清新界面版,Python代码)
摘要:动物识别系统用于识别和统计常见动物数量,通过深度学习技术检测日常几种动物图像识别,支持图片、视频和摄像头画面等形式。在介绍算法原理的同时,给出Python的实现代码、训练数据集以及PyQt的UI界面。动物识别系统主要用于常…...

K8S集群之-ETCD集群监控
### 生产ETCD集群监控核心指标 etcd服务存活状态 up{job~"kubernetes-etcd.*"}0 说明:up0代表服务挂掉 etcd是否有脱离情况 etcd_server_has_leader{job~"kubernetes-etcd.*"}0 说明:每个instance,该值应该都…...
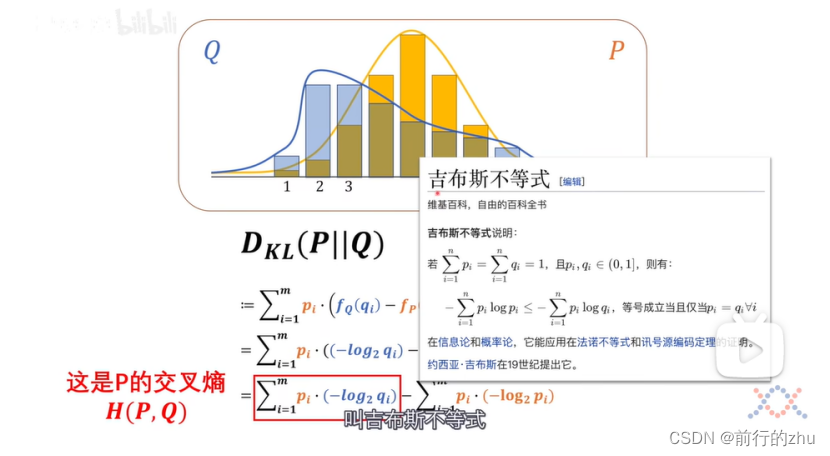
一文弄懂熵、交叉熵和kl散度(相对熵)
一个系统中事件发生的概率越大,也就是其确定性越大,则其包含的信息量越少,可以认为一个事件的信息量就是该事件发生难度的度量,事件所包含的信息量越大则其发生的难度越大。并且相互独立的事件,信息量具有可加性。相互…...
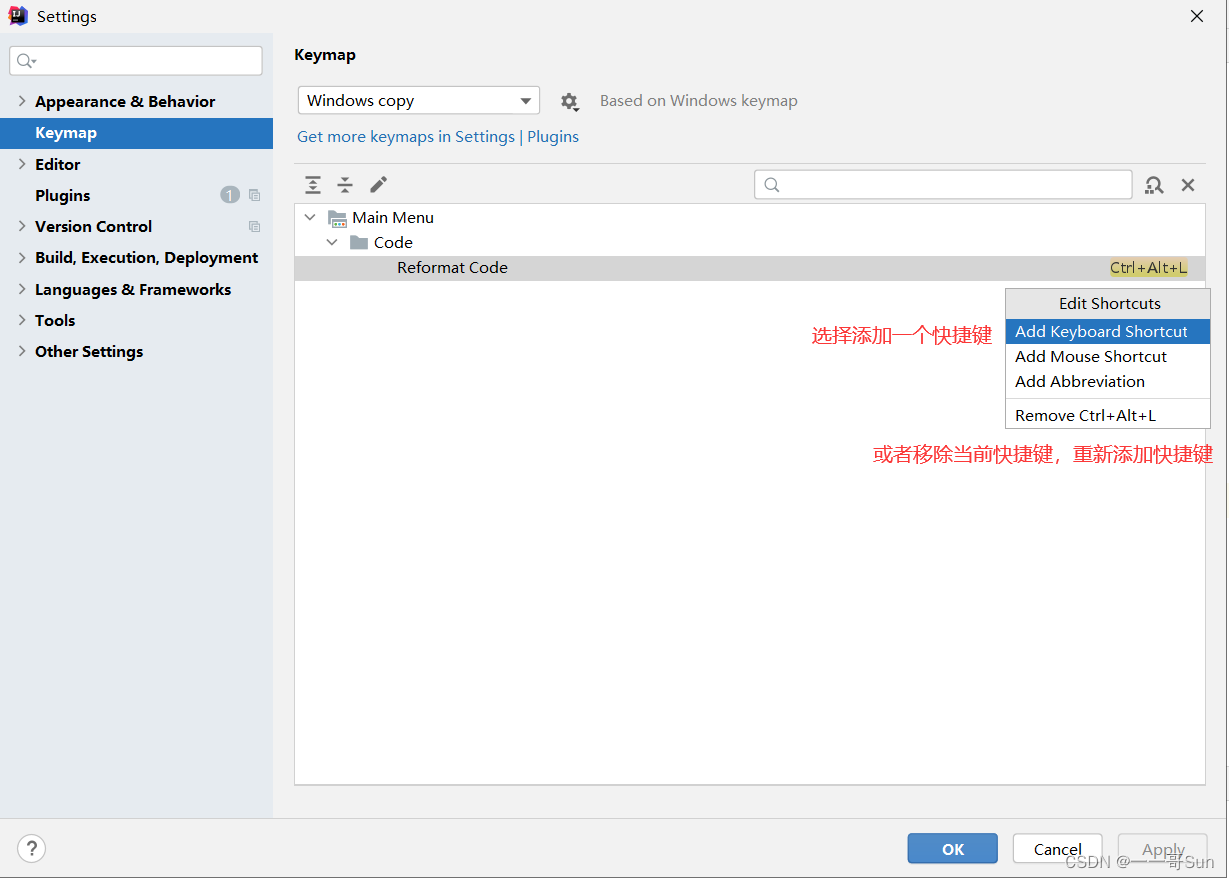
10从零开始学Java之开发Java必备软件Intellij idea的安装配置与使用
作者:孙玉昌,昵称【一一哥】,另外【壹壹哥】也是我哦CSDN博客专家、万粉博主、阿里云专家博主、掘金优质作者前言壹哥在前面的文章中,带大家下载、安装、配置了Eclipse这个更好用的IDE开发工具,并教会了大家如何在Ecli…...

04 - 进程参数编程
---- 整理自狄泰软件唐佐林老师课程 查看所有文章链接:(更新中)Linux系统编程训练营 - 目录 文章目录1. 问题1.1 再论execve(...)1.2 main函数(默认进程入口)1.3 进程空间概要图1.4 编程实验:进程参数剖析1…...

【python进阶】你真的懂元组吗?不仅是“不可变的列表”
📚引言 🙋♂️作者简介:生鱼同学,大数据科学与技术专业硕士在读👨🎓,曾获得华为杯数学建模国家二等奖🏆,MathorCup 数学建模竞赛国家二等奖🏅,…...
第13章编程练习)
《C++ Primer Plus》(第6版)第13章编程练习
《C Primer Plus》(第6版)第13章编程练习《C Primer Plus》(第6版)第13章编程练习1. Cd类2. 使用动态内存分配重做练习13. baseDMA、lacksDMA、hasDMA类4. Port类和VintagePort类《C Primer Plus》(第6版)第…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...
