决策树可解释性分析
决策树可解释性分析
决策树是一种广泛使用的机器学习算法,以其直观的结构和可解释性而闻名。在许多应用场景中,尤其是金融、医疗等领域,模型的可解释性至关重要。本文将从决策路径、节点信息、特征重要性等多个方面分析决策树的可解释性,并提供相应的代码实现。
决策树可解释性分析
- 决策树可解释性分析
- 1. 决策树的基本结构
- 2. 决策路径
- 2.1 决策路径的概念
- 2.2 决策路径的可解释性
- 3. 节点信息
- 3.1 节点信息的可解释性
- 4. 特征重要性
- 4.1 特征重要性的计算
- 5. 代码实现
- 5.1 安装依赖
1. 决策树的基本结构
决策树以树形结构表示模型的决策过程。每个节点代表一个特征的测试,每条边代表测试结果的分支,叶子节点代表最终的预测结果。决策树的可解释性主要来源于其简单直观的结构,用户可以通过观察树的分裂过程理解模型的决策依据。

2. 决策路径
2.1 决策路径的概念
决策路径是指从根节点到达某个叶子节点的路径。通过分析决策路径,我们可以理解模型在特定样本上的预测依据。例如,在某个节点上,模型可能会根据特征A的值进行分裂,然后根据特征B的值进一步分裂,最终得出分类结果。
2.2 决策路径的可解释性
- 透明性:决策树的每一步决策都可以通过简单的条件判断表示,用户可以直观地理解模型的决策过程。
- 示例分析:通过分析具体样本的决策路径,可以清晰地看到哪些特征对最终预测产生了影响。
3. 节点信息
每个节点的信息可以提供关于模型决策的更多细节。节点信息通常包括以下内容:
- 特征名称:用于分裂的特征。
- 分裂阈值:特征的分裂条件。
- 样本数量:在该节点上的样本数量。
- 类别分布:在该节点上各类别的样本分布。
3.1 节点信息的可解释性
- 特征重要性:通过查看每个节点的信息,可以评估特征在模型中的重要性。例如,某个特征在多个节点中频繁出现,说明该特征对模型决策的影响较大。
- 样本分布:节点的样本数量和类别分布可以帮助我们理解模型在特定条件下的决策依据,从而识别潜在的偏差。
4. 特征重要性
特征重要性是评估模型可解释性的重要指标。决策树模型可以计算每个特征对最终预测的贡献程度。
4.1 特征重要性的计算
特征重要性可以通过以下方式计算:
- 基于分裂增益:每次分裂所带来的信息增益可以累积到特征上,最终得到特征的重要性评分。
- 基于节点不纯度:使用基尼指数或信息增益等指标,计算每个特征在树中分裂的贡献。
5. 代码实现
下面是一个简单的代码实现,展示如何使用scikit-learn构建决策树并分析其可解释性。
5.1 安装依赖
确保已安装scikit-learn和matplotlib库:
pip install scikit-learn matplotlib
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier, export_text, plot_tree# 加载数据
data = load_iris()
X = data.data
y = data.target
feature_names = data.feature_names# 创建决策树模型
tree_model = DecisionTreeClassifier(max_depth=3, random_state=42)
tree_model.fit(X, y)# 1. 决策路径示例
sample_index = 0 # 选择第一个样本
decision_path = tree_model.decision_path(X[sample_index].reshape(1, -1))
print(f"样本 {sample_index} 的决策路径:")
print(decision_path)# 2. 节点信息
tree_rules = export_text(tree_model, feature_names=feature_names)
print("\n决策树规则:")
print(tree_rules)# 3. 特征重要性
importance = tree_model.feature_importances_
feature_importance_df = pd.DataFrame({'Feature': feature_names,'Importance': importance
}).sort_values(by='Importance', ascending=False)print("\n特征重要性:")
print(feature_importance_df)# 4. 可视化决策树
plt.figure(figsize=(12, 8))
plot_tree(tree_model, feature_names=feature_names, filled=True)
plt.title("决策树可视化")
plt.show()
相关文章:

决策树可解释性分析
决策树可解释性分析 决策树是一种广泛使用的机器学习算法,以其直观的结构和可解释性而闻名。在许多应用场景中,尤其是金融、医疗等领域,模型的可解释性至关重要。本文将从决策路径、节点信息、特征重要性等多个方面分析决策树的可解释性&…...

BUGKU-WEB never_give_up
解题思路 F12查看请求和响应,查找线索 相关工具 base64解码URL解码Burp Suit抓包 页面源码提示 <!--1p.html--> 2. 去访问这个文件,发现直接跳转到BUGKU首页,有猫腻那就下载看看这个文件内容吧 爬虫下载这个文件 import requests …...

hive自动安装脚本
使用该脚本注意事项 安装hive之前确定机子有网络。或者yum 更改为本地源,因为会使用epel仓库下载一个pv的软件使用该脚本前提是自行安装好mysql数据库准备好tomcat软件包,该脚本使用tomcat9.x版本测试过能正常执行安装成功,其他版本没有测试…...

unix 用户态 内核态
在UNIX操作系统中,"用户态"和"内核态"是两种不同的运行模式,它们定义了程序在执行时的权限级别: 用户态(User Mode): 用户态是程序运行的常规状态,大多数应用程序在执行时…...

GD32 IAP升级——boot和app相互切换
GD32 IAP升级——boot和app相互切换 目录 GD32 IAP升级——boot和app相互切换1 Keil工程设置1.1 修改ROM1.2 Keil烧录配置 2 代码编写2.1 app跳转2.2 软件重启2.3 app中断向量表偏移 结束语 1 Keil工程设置 1.1 修改ROM GD32内部Flash是一整块连续的内存,但是因为…...

C++11革新之旅:探索C++编程的无限可能
C11革新之旅:探索C编程的无限可能 C11,作为C语言的一个重要标准,为C编程带来了革命性的变革。它不仅引入了众多新特性和改进,还极大地增强了C的表达能力、提高了程序的性能和资源利用率。本文将从多个方面深入探讨C11的新特性&am…...

免费自动化AI视频剪辑工具
下载地址:https://pan.quark.cn/s/3c5995da512e FunClip是一款完全开源、本地部署的自动化视频剪辑工具,通过调用阿里巴巴通义实验室开源的FunASR Paraformer系列模型进行视频的语音识别,随后用户可以自由选择识别结果中的文本片段或说话人&a…...

Linux中安装C#的.net,创建运行后端或控制台项目
安装脚本命令: 创建一个sh文件并将该文件更改权限运行 sudo apt update wget https://packages.microsoft.com/config/ubuntu/20.04/packages-microsoft-prod.deb -O packages-microsoft-prod.deb sudo dpkg -i packages-microsoft-prod.deb sudo apt-get upd…...

最长上升子序列LIS(一般+优化)
1. 题目 题目链接: B3637 最长上升子序列 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 输入样例: 6 1 2 4 1 3 4 输出样例: 4 说明/提示: 分别取出 1、2、3、4 即可。 2. 具体实现 2.1 一般做法 dp[i]表示第i个位置的…...

【Python系列】Python 协程:并发编程的新篇章
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...

详解C/C++输入输出
前言 C/C输入输出很多,在不同的情况会用不同的输入输出,有的题目在输入时可能换一种输入输出就能不会TLE,有的输入可能要循环输入,但是可以换一种输入直接就能把所有数据输入进去。C/C有哪些常用的输入输出,在什么时候…...

AI人工智能开发环境配置
AI人工智能 为什么使用Python来开发AI 人工智能被认为是未来的趋势技术。 已经有了许多应用程序。 因此,许多公司和研究人员都对此感兴趣。 但是这里出现的主要问题是,在哪种编程语言中可以开发这些 AI 应用程序? 有各种编程语言,…...

Tomcat 8.5 下载、安装、启动及各种问题
🥰🥰🥰来都来了,不妨点个关注叭! 👉博客主页:欢迎各位大佬!👈 本期内容主要介绍 Tomcat 8 的安装,以及可能会遇到的问题 文章目录 1. Tomcat 安装2. 可能会遇到的问题2.…...

Harbor系列之5:复制管理
Harbor的镜像复制功能 Harbor 提供镜像复制功能,允许用户以推送和拉取方式在不同 Harbor 仓库之间,以及 Harbor 与非 Harbor 仓库间(如Alibaba ACR、Quay、Aws ECR、Azu热ACR、Docker Registry、Docker Hub等)复制 image、chart …...
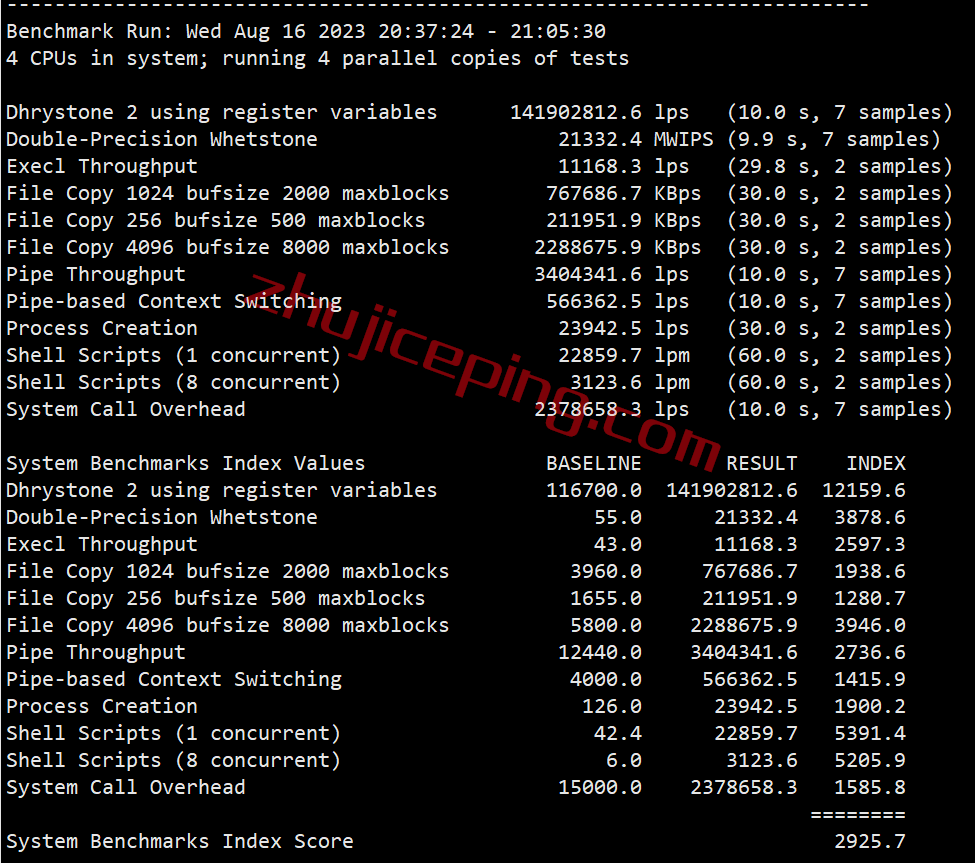
V.PS德国VPS详细测评
V.PS的德国机房位于法兰克福,默认接入电信CN2 GIA、联通CUII网络,针对中国大陆进行路由优化处理的。而且是强制移动走联通的CUII链路,确保三网都处在轻负载的网络环境下。 CPU是Intel Xeon Gold 6133 ,启用了BBR,归属德…...

【Vue3】组件通信之自定义事件
【Vue3】组件通信之自定义事件 背景简介开发环境开发步骤及源码总结 背景 随着年龄的增长,很多曾经烂熟于心的技术原理已被岁月摩擦得愈发模糊起来,技术出身的人总是很难放下一些执念,遂将这些知识整理成文,以纪念曾经努力学习奋…...

[CTF]-PWN:ORW题型综合解析
经典ORW: 例题(极客大挑战 2019 Not Bad): 这里使用mmap函数创造了一个内存映射区域 从地址0x123000开始,大小位0x1000 权限为可写可执行(可读0x1,可写0x2,可执行0x3)…...

VSCode中yarn的安装和使用
VSCode只要是做前端的,大家都不陌生,就不讲其使用了。 Yarn是一款高效、可靠的JavaScript包管理器,与NPM类似,但有其独特的优势,如更高效的安装速度、更好的依赖管理等 要在VSCode中使用Yarn,需要按照以…...

Java后端面试复习7.23
进程和线程线程优先级线程状态线程构造方式三种推荐用哪种为什么线程中断调用什么方法,本线程怎检查为什么线程不应强制停止线程通信方式四种ThreadLocalFUtureTask线程礼让终止线程的另一个缺陷(锁)守护线程什么时候设置为守护县城sleep&…...

Arduino PID库 (2) –微分导致的过冲
Arduino PID库 (2) – Derivative Kick 参考:手把手教你看懂并理解Arduino PID控制库——微分冲击 pid内容索引-CSDN博客 Arduino PID库 (1)– 简介 问题 此修改将稍微调整derivative term。目标是消除一种称为“…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...

Neko虚拟浏览器远程协作方案:Docker+内网穿透技术部署实践
前言:本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中,跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南,你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案,并结合内网…...
