三维世界,一图打尽!Matplotlib带你玩转3D绘图,让数据跳舞的魔法棒!

1. 引言
嘿,亲爱的数据探险家们!你们是否曾梦想过,在二维的屏幕上,让数据跳出束缚,翩翩起舞,展现它那迷人的三维身姿?今天,就让我这位自封的‘数据魔术师’,带你解锁Matplotlib的隐藏技能——3D绘图!想象一下,那些冷冰冰的数字和线条,在Matplotlib的魔法下,瞬间化身为立体城堡、旋转星系或是神秘迷宫。不需要复杂的咒语,只需几行代码,你就能成为这场视觉盛宴的导演。准备好了吗?让我们一起,用Matplotlib绘制3D图,让数据的世界从此不再单调,而是色彩斑斓,妙趣横生!
2. 导包
# 导包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt# 如果浏览器不显示图片,就需要加上这句话
%matplotlib inline# 让图片中可以显示中文
plt.rcParams['font.sans-serif'] = "SimHei"
# 让图片中可以显示负号
plt.rcParams["axes.unicode_minus"] = False# 支持svg矢量图
%config Inlinebackend.figure_format = "svg"# 3D引擎
from mpl_toolkits.mplot3d.axes3d import Axes3D
3. 三维折线图
fig = plt.figure(figsize=(5, 3))x = np.linspace(0, 100, 400)
y = np.sin(x)
z = np.cos(x)# 三维折线图
axes = Axes3D(fig, auto_add_to_figure=False)
fig.add_axes(axes)
axes.plot(x, y, z)
[<mpl_toolkits.mplot3d.art3d.Line3D at 0x1f0ee3b35d0>]

4. 三维散点图
fig = plt.figure(figsize=(5, 3))axes = Axes3D(fig, auto_add_to_figure=False)
fig.add_axes(axes)# 画散点图
x = np.random.rand(50)
y = np.random.rand(50)
z = np.random.rand(50)
axes.scatter(x, y, z, color="red", s=100)
<mpl_toolkits.mplot3d.art3d.Path3DCollection at 0x1f0ee1b2e90>

5. 三维柱形图
fig = plt.figure(figsize=(5, 3))axes = Axes3D(fig, auto_add_to_figure=False)
fig.add_axes(axes)x = np.arange(1, 5)
for m in x:axes.bar(np.arange(4), # y轴np.random.randint(10, 100, size=4), # z轴zs=m, # 在x轴的第几个zdir="x", # 在哪个方向上排列width=0.6,alpha=0.7)axes.set_xlabel("X轴", fontsize=10, color="r")
axes.set_ylabel("Y轴", fontsize=10, color="g")
axes.set_zlabel("Z轴", fontsize=10, color="b", labelpad=-17)plt.show()

相关文章:

三维世界,一图打尽!Matplotlib带你玩转3D绘图,让数据跳舞的魔法棒!
1. 引言 嘿,亲爱的数据探险家们!你们是否曾梦想过,在二维的屏幕上,让数据跳出束缚,翩翩起舞,展现它那迷人的三维身姿?今天,就让我这位自封的‘数据魔术师’,带你解锁Mat…...

计算机常识与NOIP历史-CSP初赛知识点整理
真题练习 [2021-CSP-J-第2题] 以下奖项与计算机领域最相关的是( )。 A.奥斯卡奖 B.图灵奖 C.诺贝尔奖 D.普利策奖 [2017-NOIP-第7题] 中国计算机学会于( )年创办全国青少年计算机程序设计竞赛。 A. 1983 B. 1984 C. 1985 D. 1986 [2018-NOIP-第5题…...

代码随想录算法训练营第二天 | 209. 长度最小的子数组、59. 螺旋矩阵 II
目录 209. 长度最小的子数组1、题目描述2、思路3、code4、复杂度分析 LC59 螺旋矩阵 II1、题目描述2、思路3、code4、复杂度分析 209. 长度最小的子数组 题目链接:209 1、题目描述 给定一个含有 n 个正整数的数组和一个正整数 target 。找出该数组中满足其总和大于…...
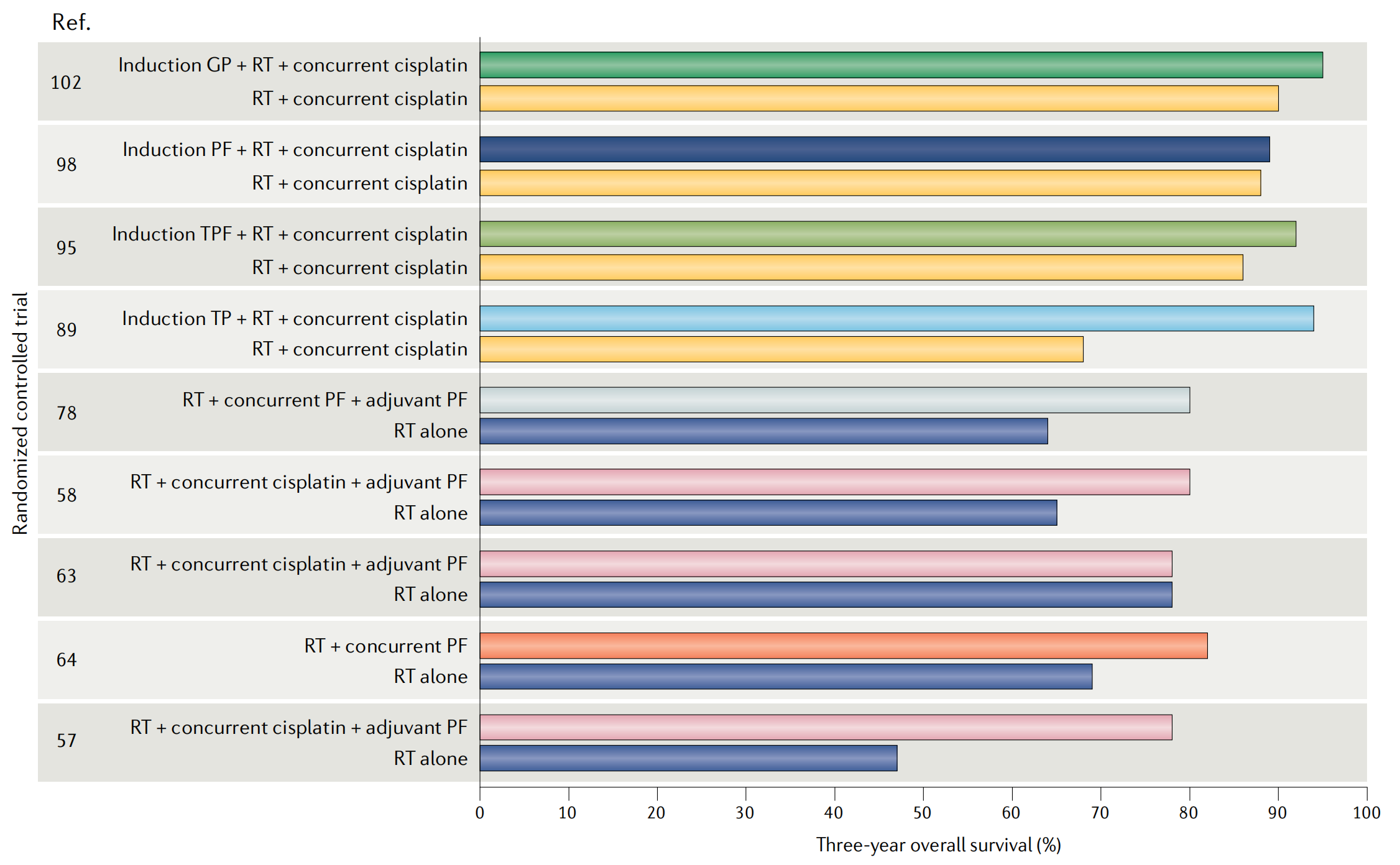
鼻咽癌综述
小罗碎碎念 本期推文主题:鼻咽癌综述 这篇文章提供了一个全面的综述,探讨了鼻咽癌(NPC)的关键研究进展,包括病理机制、治疗、筛查和生物标志物的发展。 文章首先强调了NPC在特定地理区域的流行情况,并讨论了…...

中国AI PC行业研究报告
核心摘要: 2020-2023年中国笔电出货量呈下降趋势,PC厂商亟需从产品形态、软硬技术、需求场景等角度寻求新的增长机会。而随着大模型、生成式AI技术的到来,其强大的数据处理、学习泛化与内容生成能力,高质效加速了各行各业人工智能…...

Mybatis实战:图书管理系统(笔记)
前言:如果在接口的声明方法中鼠标右键没有Test的单元测试。 你的鼠标光标问题:要在花括号范围内!!!! 数据库表是应⽤程序开发中的⼀个重要环节, 数据库表的设计往往会决定我们的应⽤需求是否能顺利实现, 甚…...

win11 amd64 python安装matplotlib、pytorch报错记录
win11 amd64 python matplotlib 安装报错记录 安装时 错误是 metadata-generation-failed 查看上面的具体报错原因,来自: Files\Python\Python3_10_11\Include: linker input file not found: No such file or director注意Python 的路径中最好不要有…...
)
Python写UI自动化--playwright(等待页面加载机制)
很多情况下,我们都需要等待页面加载到一定程度才能进行下一步操作,而这个度该怎么操作,这篇文章就来详细讲一讲 目录 expect_popup() wait_until参数 "load" commit: "domcontentloaded" "networkidle"…...
0804)
书籍将整数字符串转成整数值(5)0804
题目 给定一个字符串str,如果str符合日常书写的整数形式,并且属于32位整数的范围,返回str所代表的整数值,否则返回0。 举例 str“123” 返回 123 str“023” 因为023 不符合日常的书写习惯,所以返回0 str“A13” …...

【2024年华数杯C题老外游中国】(完整题解+代码+完整参考论文)
请问 352 个城市中所有 35200 个景点评分的最高分(Best Score,简称 BS)是多少?全国有多少个景点获评了这个最高评分(BS)?获评了这个最高评分(BS)景点最多的城市有哪些&am…...

全球氢化双酚A (HBPA)市场规划预测:2030年市场规模将接近1330亿元,未来六年CAGR为2.7%
一、引言 随着全球化工行业的持续发展,氢化双酚A (HBPA)作为重要的化工原料,其市场重要性日益凸显。本文旨在探索HBPA行业的发展趋势、潜在商机及其未来展望。 二、市场趋势 全球HBPA市场的增长主要受全球化工行业增加、消费者对高性能化工产品要求提高…...

【C++】异常处理:深度解析与实战精髓,不容错过的编程秘籍
🌈 个人主页:Zfox_ 🔥 系列专栏:C从入门到精通 目录 🚀 前言:C语言传统的处理错误的方式 一: 🔥 C异常概念二: 🔥 异常的使用 2.1 📖 异常的抛出和…...

智能指针的循环引用 是什么 怎么引起的
智能指针的循环引用 是什么 怎么引起的 智能指针的循环引用(Circular Reference)是指两个或多个对象之间的共享指针相互引用,导致这些对象永远不会被释放,从而引发内存泄露。主要发生在使用std::shared_ptr时,因为它们…...

Stegdetect教程:如何用Stegdetect检测和破解JPG图像隐写信息
一、Stegdetect简介 Stegdetect 是一个开源工具,专门设计用于检测图像文件(JPG格式)中的隐写信息。Stegdetect 可以检测多种常见的隐写方法,比如 JSteg、JPHide 和 OutGuess 等。 二、使用Stegdetect检测图像隐写 官方描述&#…...

Co-Detr
参考:https://www.bilibili.com/video/BV1Sh4y1F7ur/?spm_id_from333.788&vd_source156234c72054035c149dcb072202e6be 之前的detr正样本数量少,匹配不平衡。 主要修改两个地方:encoder和decoder。 1.在encoder之后加入RPN,a…...

校园选课助手【1】-项目整体架构从此开始
项目背景 随着高校招生规模的不断扩大,学生选课需求日益增长。为提高选课效率,降低学生选课压力,本项目旨在开发一款校园选课助手软件。 项目目标:开发一款具有以下特点的校园选课助手软件: 易用性:界面简洁ÿ…...

椭圆曲线加法运算
1. 定义 椭圆曲线 (Elliptic Curve) 不是函数,而是一条平面曲线,其方程是定义如下: y 2 x 3 a x b y^2x^3axb y2x3axb 其中,判别式 Δ − 16 ( 4 a 3 27 b 2 ) ≠ 0 \Delta -16(4a^327b^2)\neq 0 Δ−16(4a327b2)0。判别…...

(STM32笔记)九、RCC时钟树与时钟 第一部分
我用的是正点的STM32F103来进行学习,板子和教程是野火的指南者。 之后的这个系列笔记开头未标明的话,用的也是这个板子和教程。 九、RCC时钟树与时钟 九、RCC时钟树与时钟1、时钟树HSE时钟HSI时钟锁相环时钟系统时钟HCLK时钟PCLK1时钟PCLK2时钟RTC时钟独…...
fastjson-流程分析
参考视频:fasfjson反序列化漏洞1-流程分析 分析版本 fastjson1.2.24 JDK 8u65 分析过程 新建Person类 public class Person {private String name;private int age;public Person() {System.out.println("constructor_0");}public Person(String na…...
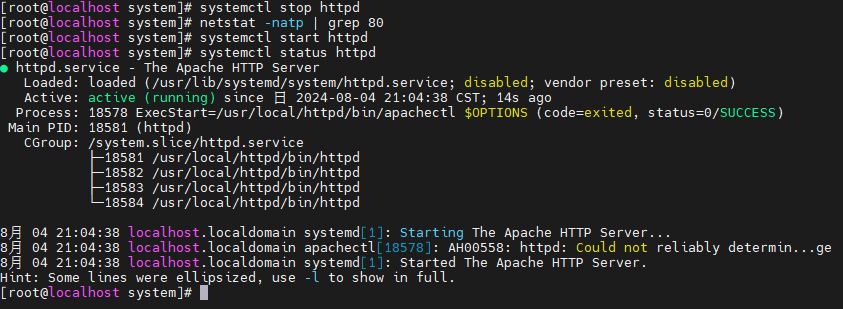
Linux 命令安装
系列文章目录 提示:仅用于个人学习,进行查漏补缺使用。 1.Linux介绍、目录结构、文件基本属性、Shell 2.Linux常用命令 3.Linux文件管理 4.Linux 命令安装 提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...
