动手学深度学习V2每日笔记(卷积层)
本文主要参考沐神的视频教程 https://www.bilibili.com/video/BV1L64y1m7Nh/p=2&spm_id_from=333.1007.top_right_bar_window_history.content.click&vd_source=c7bfc6ce0ea0cbe43aa288ba2713e56d
文档教程 https://zh-v2.d2l.ai/
本文的主要内容对沐神提供的代码中个人不太理解的内容进行笔记记录,内容不会特别严谨仅供参考。
1.函数目录
1.1 python
| python | 位置 |
|---|---|
| 元组加法操作 | 2.2 |
1.2 torch
| torch.nn | 位置 |
|---|---|
| Conv2d | 2.3 |
| stack | 2.3 |
| cat | 2.3 |
2. 卷积神经网络
2.1 卷积层
卷积层将输入和核矩阵进行交叉相关运算,加上偏移后得到输出。核矩阵和偏移是可以学习的参数。核矩阵的大小是超参数。
- 交叉相关VS卷积
- 二维交叉相关
y i , j = ∑ a = 1 h ∑ b = 1 w w a , b x i + a , j + b y_{i,j}=\sum_{a=1}^h\sum_{b=1}^ww_{a,b}x_{i+a,j+b} yi,j=a=1∑hb=1∑wwa,bxi+a,j+b - 二维卷积
y i , j = ∑ a = 1 h ∑ b = 1 w w − a , − b x i + a , j + b y_{i,j}=\sum_{a=1}^h\sum_{b=1}^ww_{-a,-b}x_{i+a,j+b} yi,j=a=1∑hb=1∑ww−a,−bxi+a,j+b - 由于对称性,在实际使用中没有区别
- 一维和三维交叉相关
- 一维
y i = ∑ a = 1 h w a , x i + a y_{i}=\sum_{a=1}^hw_{a,}x_{i+a} yi=a=1∑hwa,xi+a - 文本、语言、时序序列
- 三维
y i , j , k = ∑ a = 1 h ∑ b = 1 w ∑ c = 1 d w a , b , c x i + a , j + b , k + c y_{i,j,k}=\sum_{a=1}^h\sum_{b=1}^w\sum_{c=1}^dw_{a,b,c}x_{i+a,j+b,k+c} yi,j,k=a=1∑hb=1∑wc=1∑dwa,b,cxi+a,j+b,k+c - 视频、医学图像、气象图像
2.1.1 二维互相关运算
def corr2d(X, K):"""计算二维互相关运算"""h, w = K.shapeY = torch.zeros(X.shape[0]-h+1, X.shape[1]-w+1)for i in range(Y.shape[0]):for j in range(Y.shape[1]):Y[i,j] = (X[i:i+h, j:j+w]*K).sum()return YX = torch.arange(9).reshape(3,3)
K = torch.arange(4).reshape(2,2)print(corr2d(X, K))
2.1.2 卷积层
class Conv2D(nn.Module):def __init__(self, kernel_size):super().__init__()self.weight = nn.Parameter(torch.rand(size=kernel_size))self.bias = nn.Parameter(torch.zeros(1))def forward(self, x):return corr2d(x, self.weight) + self.bias
2.1.3 完整代码
import torch
from torch import nn
from d2l import torch as d2ldef corr2d(X, K):"""计算二维互相关运算"""h, w = K.shapeY = torch.zeros(X.shape[0]-h+1, X.shape[1]-w+1)for i in range(Y.shape[0]):for j in range(Y.shape[1]):Y[i,j] = (X[i:i+h, j:j+w]*K).sum()return YX = torch.arange(9).reshape(3,3)
K = torch.arange(4).reshape(2,2)print(corr2d(X, K))
# 自定义卷积层
class Conv2D(nn.Module):def __init__(self, kernel_size):super().__init__()self.weight = nn.Parameter(torch.rand(size=kernel_size))self.bias = nn.Parameter(torch.zeros(1))def forward(self, x):return corr2d(x, self.weight) + self.bias
# 图像中目标的边沿检查
x = torch.ones((6,8))
x[:, 2:6] = 0
print(x)k = torch.tensor([[1.0, -1.0]])
Y = corr2d(x, k)
print(Y)
# 学习卷积核
Conv2d = nn.Conv2d(1, 1, kernel_size=(1,2), bias=False)
x = x.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))for i in range(10):y_hat = Conv2d(x)l = (y_hat-Y)**2Conv2d.zero_grad()l.sum().backward()Conv2d.weight.data[:] -= 3e-2 * Conv2d.weight.gradif(i+1)%2 == 0:print(f'batch{i+1}, loss{l.sum():.3f}')print(Conv2d.weight.data.reshape((1,2)))
2.2 填充和步幅
2.2.1 填充padding
在输入周围添加额外的行、列

- 填充 p h p_h ph行和 p w p_w pw列,输出的形状为
- ( n h − k h + p h + 1 ) ∗ ( n w − k w + p w + 1 ) (n_h-k_h+p_h+1)*(n_w-k_w+p_w+1) (nh−kh+ph+1)∗(nw−kw+pw+1)
2.2.2 步幅stride
- 步幅是指行/列的滑动步长
- 例如;高度3宽度2的步长

填充和步幅是卷积层的超参数
填充在输入周围添加额外的行/列,来控制输出的形状
步幅是每次滑动核窗口时的行/列的步长,可以成倍的减少输出形状
2.3.3 元组加法运算
a = (1, 1)
b = (8, 8)
print(a+b)

列表也具有相同的操作
a = [1, 1]
b = [8, 8]
print(a+b)

import torch
from torch import nndef comp_conv2d(conv2d, X):X = X.reshape((1, 1) + X.shape)Y = conv2d(X)return Y.reshape(Y.shape[2:])conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1)
X = torch.rand((8,8))
print(comp_conv2d(conv2d, X).shape)conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1, stride=2)
print(comp_conv2d(conv2d, X).shape)
2.3 多输入输出通道
2.3.1 多个输入通道
- 彩色图片可能有RGB三个通道
- 转换为灰度会丢失信息

每个通道都有一个卷积核,结果是所有通道卷积结果的和。

多个输入通道
| 输入X | 核W | 输出Y |
|---|---|---|
| c i ∗ n h ∗ n w c_i*n_h*n_w ci∗nh∗nw | c i ∗ k h ∗ k w c_i*k_h*k_w ci∗kh∗kw | m h ∗ m w m_h*m_w mh∗mw |
Y = ∑ i 0 c i X i , : , : ∗ W i , : , : Y = \sum_{i_0}^{c_i}X_{i,:,:}*W_{i,:,:} Y=i0∑ciXi,:,:∗Wi,:,:
无论有多少输入通道,到目前为止我们只用到单输出通道。
def corr2d(X, K):"""计算二维互相关运算"""h, w = K.shapeY = torch.zeros(X.shape[0]-h+1, X.shape[1]-w+1)for i in range(Y.shape[0]):for j in range(Y.shape[1]):Y[i,j] = (X[i:i+h, j:j+w]*K).sum()return Ydef corr2d_multi_in(X, K):return sum(corr2d(x,k) for x,k in zip(X, K))X = torch.tensor([[[0.0,1.0,2.0],[3.0,4.0,5.0],[6.0,7.0,8.0]],[[1.0,2.0,3.0],[4.0,5.0,6.0],[7.0,8.0,9.0]]])
K = torch.tensor([[[0.0, 1.0],[2.0, 3.0]],[[1.0,2.0],[3.0,4.0]]])
print(corr2d_multi_in(X, K))
2.3.2 多个输出通道
我们可以有多个三维卷积核,每个核生成一个输出通道。
| 输入X | 核W | 输出Y |
|---|---|---|
| c i ∗ n h ∗ n w c_i*n_h*n_w ci∗nh∗nw | c o ∗ c i ∗ k h ∗ k w c_o*c_i*k_h*k_w co∗ci∗kh∗kw | c o ∗ m h ∗ m w c_o*m_h*m_w co∗mh∗mw |
Y = ∑ i 0 c i X i , : , : ∗ W i , : , : f o r i = 1 , . . . , c o Y = \sum_{i_0}^{c_i}X_{i,:,:}*W_{i,:,:} \ for\ i=1,...,c_o Y=i0∑ciXi,:,:∗Wi,:,: for i=1,...,co
- 每个输出通道都可以识别特定模式

- 输入通道核识别并组合输入中的模式
def corr2d_multi_in_out(X, K):return torch.stack([corr2d_multi_in(X, k) for k in K], 0)K = torch.stack((K, K+1, K+2), 0)
print(K.shape)
print(corr2d_multi_in_out(X,K))
2.3.3 1*1卷积层
k h = k w = 1 k_h=k_w=1 kh=kw=1是一个受欢迎的选择。它不识别空间模式,只是融合通道。

相当于输入形状为 n h n w ∗ c i n_hn_w*c_i nhnw∗ci,权重为 c o ∗ c i {c_o*c_i} co∗ci的全连接层。
2.3.4 nn.Conv2d()
nn.Conv2d 的作用是对输入的二维数据(如图像)进行卷积操作,输出经过卷积处理后的特征图。卷积操作可以帮助网络学习到数据的局部特征,如边缘、纹理等。
torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros')
- 参数说明
- in_channels (int): 输入数据的通道数。例如,对于RGB图像,in_channels 应为 3。
- out_channels (int): 卷积层输出的通道数(即卷积核的数量)。
- kernel_size (int or tuple): 卷积核的大小。如果是整数,则表示卷积核是正方形的;如果是元组,则表示卷积核的高度和宽度。
- stride (int or tuple, 可选): 卷积核的步幅。默认值为 1。
- padding (int, tuple or str, 可选): 输入数据的填充。默认值为 0。
- dilation (int or tuple, 可选): 卷积核元素之间的间距。默认值为 1。
- groups (int, 可选): 控制输入和输出通道的连接。默认值为 1。
- bias (bool, 可选): 如果设置为 True,将会给输出添加一个可学习的偏置。默认值为 True。
- padding_mode (str, 可选): 填充模式。可选值为 ‘zeros’, ‘reflect’, ‘replicate’ 或 ‘circular’。默认值为 ‘zeros’。
输出张量的形状可以通过以下公式计算: - input: ( N , C i n , H i n , W i n ) (N,C_{in},H_{in},W_{in}) (N,Cin,Hin,Win)
- output: ( N , C o u t , H o u t , W o u t ) (N,C_{out},H_{out},W_{out}) (N,Cout,Hout,Wout)
H o u t = H i n + 2 ∗ p a d d i n g [ 0 ] − d i l a t i o n [ 0 ] ∗ ( k e r n e l _ s i z e [ 0 ] − 1 ) s t r i d e [ 0 ] H_{out}=\frac{H_{in}+2*padding[0]-dilation[0]*(kernel\_{size}[0]-1)}{stride[0]} Hout=stride[0]Hin+2∗padding[0]−dilation[0]∗(kernel_size[0]−1)
W o u t = H i n + 2 ∗ p a d d i n g [ 1 ] − d i l a t i o n [ 1 ] ∗ ( k e r n e l _ s i z e [ 1 ] − 1 ) s t r i d e [ 1 ] W_{out}=\frac{H_{in}+2*padding[1]-dilation[1]*(kernel\_{size}[1]-1)}{stride[1]} Wout=stride[1]Hin+2∗padding[1]−dilation[1]∗(kernel_size[1]−1)
import torch
import torch.nn as nn# 创建一个 Conv2d 对象
conv_layer = nn.Conv2d(in_channels=3, out_channels=16, kernel_size=3, stride=1, padding=1)# 打印 Conv2d 对象的参数
print(conv_layer)# 创建一个随机输入张量,形状为 (batch_size, in_channels, height, width)
input_tensor = torch.randn(1, 3, 32, 32)# 通过卷积层前向传播输入张量
output_tensor = conv_layer(input_tensor)# 打印输出张量的形状
print(output_tensor.shape)

对上述示例输出形状计算:
- 输入张量形状(1,3,32,32)
- 卷积核大小为3*3
- 步幅为1
- 填充为1
输出高度
H o u t = 32 − 2 ∗ 1 + 3 − 1 1 = 32 H_{out}=\frac{32-2*1+3-1}{1}=32 Hout=132−2∗1+3−1=32
输出宽度
W o u t = 32 − 2 ∗ 1 + 3 − 1 1 = 32 W_{out}=\frac{32-2*1+3-1}{1}=32 Wout=132−2∗1+3−1=32
2.3.5 stack
torch.stack 是 PyTorch 中的一个函数,用于沿新维度连接一系列张量。它的作用类似于 torch.cat,但不同的是,torch.cat 是在现有维度上进行连接,而 torch.stack 会在指定的维度上插入一个新的维度,然后在这个新维度上进行连接。
torch.stack(tensors, dim=0)
参数
- tensors (sequence of Tensors): 要连接的张量序列。
- dim (int): 新插入维度的索引位置。默认值为 0。
| Tensor1.shape | Tensor2.shape | dim | out |
|---|---|---|---|
| (3,3) | (3,3) | 0 | (2,2,3) |
| (3,3) | (3,3) | 1 | (3,2,3) |
| (3,3) | (3,3) | 2 | (3,3,2) |
沿着维度0进行stack
import torch# 创建两个相同形状的张量
x = torch.arange(9).reshape(3,3)
y = torch.randn(3,3)
# 沿着0维度
z = torch.stack([x,y],0)
z
tensor([[[ 0.0000, 1.0000, 2.0000],[ 3.0000, 4.0000, 5.0000],[ 6.0000, 7.0000, 8.0000]],[[ 0.8259, -1.7941, 0.8862],[ 0.6030, -0.7413, 0.7847],[-0.0850, 0.7196, -0.7993]]])
z.shape
torch.Size([2, 3, 3])
沿着维度1进行stack
z1 = torch.stack((x,y),1)
z1
tensor([[[ 0.0000, 1.0000, 2.0000],[ 0.8259, -1.7941, 0.8862]],[[ 3.0000, 4.0000, 5.0000],[ 0.6030, -0.7413, 0.7847]],[[ 6.0000, 7.0000, 8.0000],[-0.0850, 0.7196, -0.7993]]])
z1.shape
torch.Size([3, 2, 3])
沿着维度2进行stack
z2 = torch.stack((x,y),2)
z2
tensor([[[ 0.0000, 0.8259],[ 1.0000, -1.7941],[ 2.0000, 0.8862]],[[ 3.0000, 0.6030],[ 4.0000, -0.7413],[ 5.0000, 0.7847]],[[ 6.0000, -0.0850],[ 7.0000, 0.7196],[ 8.0000, -0.7993]]])
z2.shape
torch.Size([3, 3, 2])
2.3.6 cat
torch.cat 是 PyTorch 中的一个函数,用于沿已有的维度连接一系列张量。与 torch.stack 不同的是,torch.cat 不会在连接过程中创建新的维度,而是直接在指定的维度上进行连接。
torch.cat(tensors, dim=0)
- 参数
- tensors (sequence of Tensors): 要连接的张量序列,这些张量在除 dim 维之外的其他维度上必须具有相同的形状。
- dim (int): 指定在该维度上连接张量。默认值为 0。
| Tensor1.shape | Tensor2.shape | dim | out |
|---|---|---|---|
| (3,3) | (3,3) | 0 | (6,3) |
| (3,3) | (3,3) | 1 | (3,6) |
沿着维度0进行cat
c0 = torch.cat((x,y),0)
c0
tensor([[ 0.0000, 1.0000, 2.0000],[ 3.0000, 4.0000, 5.0000],[ 6.0000, 7.0000, 8.0000],[ 0.8259, -1.7941, 0.8862],[ 0.6030, -0.7413, 0.7847],[-0.0850, 0.7196, -0.7993]])
c0.shape
torch.Size([6, 3])
沿着维度1进行cat
c1 =torch.cat((x,y),1)
c1
tensor([[ 0.0000, 1.0000, 2.0000, 0.8259, -1.7941, 0.8862],[ 3.0000, 4.0000, 5.0000, 0.6030, -0.7413, 0.7847],[ 6.0000, 7.0000, 8.0000, -0.0850, 0.7196, -0.7993]])
c1.shape
torch.Size([3, 6])
2.3.7 完整代码
import torch
from torch import nndef comp_conv2d(conv2d, X):X = X.reshape((1, 1) + X.shape)Y = conv2d(X)return Y.reshape(Y.shape[2:])conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1)
X = torch.rand((8,8))
print(comp_conv2d(conv2d, X).shape)conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1, stride=2)
print(comp_conv2d(conv2d, X).shape)def corr2d(X, K):"""计算二维互相关运算"""h, w = K.shapeY = torch.zeros(X.shape[0]-h+1, X.shape[1]-w+1)for i in range(Y.shape[0]):for j in range(Y.shape[1]):Y[i,j] = (X[i:i+h, j:j+w]*K).sum()return Ydef corr2d_multi_in(X, K):return sum(corr2d(x,k) for x,k in zip(X, K))X = torch.tensor([[[0.0,1.0,2.0],[3.0,4.0,5.0],[6.0,7.0,8.0]],[[1.0,2.0,3.0],[4.0,5.0,6.0],[7.0,8.0,9.0]]])
K = torch.tensor([[[0.0, 1.0],[2.0, 3.0]],[[1.0,2.0],[3.0,4.0]]])
print(corr2d_multi_in(X, K))def corr2d_multi_in_out(X, K):return torch.stack([corr2d_multi_in(X, k) for k in K], 0)K = torch.stack((K, K+1, K+2), 0)
print(K.shape)
print(corr2d_multi_in_out(X,K))
相关文章:

动手学深度学习V2每日笔记(卷积层)
本文主要参考沐神的视频教程 https://www.bilibili.com/video/BV1L64y1m7Nh/p2&spm_id_from333.1007.top_right_bar_window_history.content.click&vd_sourcec7bfc6ce0ea0cbe43aa288ba2713e56d 文档教程 https://zh-v2.d2l.ai/ 本文的主要内容对沐神提供的代码中个人不…...

qcom ucsi probe
ucsi glink 注册一个ucsi 设备,和pmic glink进行通信,ucsi作为pmic glink的一个client。 lkml的patch https://lkml.org/lkml/2023/1/30/233 dtsi中一般会定义 qcom,ucsi-glink 信息,用于和驱动进行匹配 static const struct of_device_id …...

flask和redis配合
对于涉及数据提交的场景,比如更新用户信息,你可能会使用POST或PUT请求。但是,这些操作通常与直接从Redis缓存中检索数据不同,因为它们可能涉及到对后端数据库或其他存储系统的修改。并且可能需要将更新后的数据同步回Redis缓存&am…...

深度学习中的早停法
早停法(Early Stopping)是一种用于防止模型过拟合的技术,在训练过程中监视验证集(或者测试集)上的损失值。具体设立早停的限制包括两个主要参数: Patience(耐心):这是指验…...

科普文:JUC系列之多线程门闩同步器CountDownLatch的使用和源码
CountDownLatch类位于java.util.concurrent包下,利用它可以实现类似计数器的功能。比如有一个任务A,它要等待其他10个线程的任务执行完毕之后才能执行,此时就可以利用CountDownLatch来实现这种功能了。 CountDownLatch是通过一个计数器来实现…...

foreach循环和for循环在PHP中各有什么优势
在PHP中,foreach循环和for循环都是用来遍历数组的常用结构,但它们各有其优势和使用场景。 foreach循环的优势 简化代码:foreach循环提供了一种更简洁的方式来遍历数组,不需要手动控制索引或指针。易于阅读:对于简单的…...

巧用casaos共享挂载自己的外接硬盘为局域网共享
最近入手了个魔改机顶盒,已经刷好了的armbian,虽然是原生的,但是我觉得挺强大的,内置了很多 常用的docker和应用,只需要armbian-software 安装就行,缺点就是emmc太小了。 买到之后第一时间装上了casaos和1p…...

标题:解码“八股文”:助力、阻力,还是空谈?
标题:解码“八股文”:助力、阻力,还是空谈? 在程序员的面试与职场发展中,“八股文”一直是一个备受争议的话题。它既是求职者展示自己技术功底的途径,也是一些公司筛选人才的标准之一。但“八股文”在实际…...

语言无界,沟通无限:2024年好用在线翻译工具推荐
随着技术的发展现在的翻译在线工具从基础词句翻译到复杂的文章翻译都不在话下。为了防止你被五花八门的工具挑花眼,我给你介绍几款我用过的便捷、高效、准确的翻译工具吧。 1.福晰翻译端 链接直通:https://www.foxitsoftware.cn/fanyi/ 这个软件支持…...

【Golang 面试 - 进阶题】每日 3 题(十八)
✍个人博客:Pandaconda-CSDN博客 📣专栏地址:http://t.csdnimg.cn/UWz06 📚专栏简介:在这个专栏中,我将会分享 Golang 面试中常见的面试题给大家~ ❤️如果有收获的话,欢迎点赞👍收藏…...

二分+dp,CF 1993D - Med-imize
一、题目 1、题目描述 2、输入输出 2.1输入 2.2输出 3、原题链接 D - Med-imize 二、解题报告 1、思路分析 对于n < k的情况直接排序就行 对于n > k的情况 最终的序列长度一定是 (n - 1) % k 1 这个序列是原数组的一个子序列 对于该序列的第一个元素࿰…...

三十种未授权访问漏洞复现 合集( 三)
未授权访问漏洞介绍 未授权访问可以理解为需要安全配置或权限认证的地址、授权页面存在缺陷,导致其他用户可以直接访问,从而引发重要权限可被操作、数据库、网站目录等敏感信息泄露。---->目录遍历 目前主要存在未授权访问漏洞的有:NFS服务&a…...
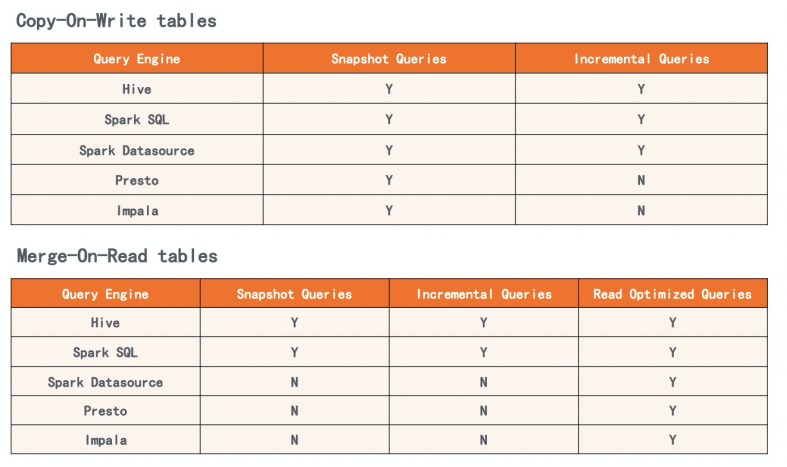
数据湖和数据仓库核心概念与对比
随着近几年数据湖概念的兴起,业界对于数据仓库和数据湖的对比甚至争论就一直不断。有人说数据湖是下一代大数据平台,各大云厂商也在纷纷的提出自己的数据湖解决方案,一些云数仓产品也增加了和数据湖联动的特性。但是数据仓库和数据湖的区别到…...

探索WebKit的奥秘:打造高效、兼容的现代网页应用
1. 简介 1.1. 主要特点 WebKit 是一个开源的浏览器引擎,它允许开发者构建高性能、功能丰富的 web 应用程序。WebKit 与 Mozilla Firefox 等使用的 Gecko 引擎、Internet Explorer 使用的 Trident 引擎以及 EdgeHTML 引擎共同构成了现代 web 浏览器的核心技术。 1.2. 学习资…...

【leetcode】平衡二叉树、对称二叉树、二叉树的层序遍历(广度优先遍历)(详解)
Hi~!这里是奋斗的明志,很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~~ 🌱🌱个人主页:奋斗的明志 🌱🌱所属专栏:数据结构、LeetCode专栏 📚本系…...

最短路径算法:Floyd-Warshall算法
引言 在图论中,Floyd-Warshall算法是一种用于计算任意两点之间最短路径的动态规划算法。它适用于加权有向图和无向图,可以处理带有负权重边的图,但要求图中不能有负权重环。本文将详细介绍Floyd-Warshall算法的定义、步骤及其实现。 Floyd-…...

3DM游戏运行库合集离线安装包2024最新版
3DM游戏运行库合集离线安装包是一款由国内最大的游戏玩家论坛社区3DM推出的集成式游戏运行库合集软件,旨在解决玩家在玩游戏时遇到的运行库缺失或错误问题。该软件包含多种常用的系统运行库组件,支持32位和64位操作系统,能够自动识别系统版本…...

【Bigdata】什么是混合型联机分析处理
这是我父亲 日记里的文字 这是他的生命 留下留下来的散文诗 几十年后 我看着泪流不止 可我的父亲已经 老得像一个影子 🎵 许飞《父亲写的散文诗》 混合型联机分析处理(Hybrid OLAP,简称 HOLAP)是一种结合了多…...

Java 并发编程:volatile 关键字介绍与使用
大家好,我是栗筝i,这篇文章是我的 “栗筝i 的 Java 技术栈” 专栏的第 026 篇文章,在 “栗筝i 的 Java 技术栈” 这个专栏中我会持续为大家更新 Java 技术相关全套技术栈内容。专栏的主要目标是已经有一定 Java 开发经验,并希望进…...

【Spark计算引擎----第三篇(RDD)---《深入理解 RDD:依赖、Spark 流程、Shuffle 与缓存》】
前言: 💞💞大家好,我是书生♡,本阶段和大家一起分享和探索大数据技术Spark—RDD,本篇文章主要讲述了:RDD的依赖、Spark 流程、Shuffle 与缓存等等。欢迎大家一起探索讨论!࿰…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...
