浅谈KMP算法(c++)
目录
- 前缀函数
- 应用
- 【模板】KMP
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 样例 1 解释
- 数据规模与约定
- 思路
- AC代码
- 本质不同子串数
- 例题讲解
- [NOI2014] 动物园
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 思路
- AC代码
- [POI2006] OKR-Periods of Words
- 题面翻译
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 思路
- AC代码
- [BOI2009] Radio Transmission 无线传输
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 样例输入输出 1 解释
- 规模与约定
- 思路
- AC代码
- [COCI2011-2012#4] KRIPTOGRAM
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 样例 #2
- 样例输入 #2
- 样例输出 #2
- 样例 #3
- 样例输入 #3
- 样例输出 #3
- 提示
- 思路
- AC代码
为方便讲述,字符串下标从 开始
前缀函数
给定一个长度为 n n n的字符串 s s s其前缀函数定义为一个长度为 n n n的数组 π \pi π, π i \pi_i πi 为子串 s [ 0 , 1 , … … i ] s[0,1,……i] s[0,1,……i]的所有相等的真前缀和真后缀(称为border)的最长长度,若没有则为.
朴素求解前缀函数
int n = (int)s.length();
vector<int> pi(n);
for (int i = 1; i < n; i++)
for (int j = i; j >= 0; j--)
if (s.substr(0, j) == s.substr(i - j + 1, j)) {pi[i] = j;break;
}
这显然是一个 n 3 n^3 n3的算法
我们可以通过一些观察来优化这个算法。
- π i + 1 ≤ π i + 1 \pi _{i+1} \leq \pi_i +1 πi+1≤πi+1 反证即可,假设 π i + 1 \pi_{i+1} πi+1更大,那 π i \pi_i πi也应该更大
通过这个我们可以把原来的暴力优化成 但这还不够优秀 - 如果失配,我们可以利用之前已经处理过的信息来避免一些重复比较
考虑我们当前已经处理完前 i i i为,且第 i + 1 i+1 i+1位失配,即 s i ≠ s π i + 1 s_i\neq s_{\pi_i+1} si=sπi+1,我们想快速找到最长的新匹配。
由 border 的定义,也就是我们要找到最大的j使得 s i , j = s i = j + 1 , i s_{i,j}=s_{i=j+1,i} si,j=si=j+1,i^ s j + 1 = s i + 1 s_{j+1}=s_{i+1} sj+1=si+1
只考虑第一个条件,事实上 j = π π i j=\pi_{\pi_i} j=ππi
证明: - π π i \pi_{\pi_i} ππi满足条件1 ,手模一下即可。
- π π i \pi_{\pi_i} ππi是最大的满足条件的,反证即可。
通过以上两个观察,我们就可以得出最终的算法,也就是 KMP
for(int i = 2, j = 0; i <= n; ++i){
while(j && s[j + 1] != s[i])j = nxt[j];
if(s[j + 1] == s[i]) ++j;
nxt[i] = j;
}
时间复杂度由 while 循环计算,复杂度 O ( n ) O(n) O(n)
应用
字符串匹配
【模板】KMP
题目描述
给出两个字符串 s 1 s_1 s1 和 s 2 s_2 s2,若 s 1 s_1 s1 的区间 [ l , r ] [l, r] [l,r] 子串与 s 2 s_2 s2 完全相同,则称 s 2 s_2 s2 在 s 1 s_1 s1 中出现了,其出现位置为 l l l。
现在请你求出 s 2 s_2 s2 在 s 1 s_1 s1 中所有出现的位置。
定义一个字符串 s s s 的 border 为 s s s 的一个非 s s s 本身的子串 t t t,满足 t t t 既是 s s s 的前缀,又是 s s s 的后缀。
对于 s 2 s_2 s2,你还需要求出对于其每个前缀 s ′ s' s′ 的最长 border t ′ t' t′ 的长度。
输入格式
第一行为一个字符串,即为 s 1 s_1 s1。
第二行为一个字符串,即为 s 2 s_2 s2。
输出格式
首先输出若干行,每行一个整数,按从小到大的顺序输出 s 2 s_2 s2 在 s 1 s_1 s1 中出现的位置。
最后一行输出 ∣ s 2 ∣ |s_2| ∣s2∣ 个整数,第 i i i 个整数表示 s 2 s_2 s2 的长度为 i i i 的前缀的最长 border 长度。
样例 #1
样例输入 #1
ABABABC
ABA
样例输出 #1
1
3
0 0 1
提示
样例 1 解释
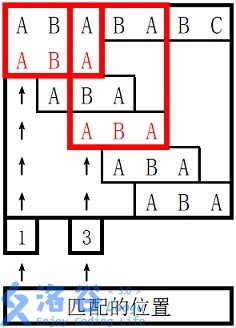 。
。
对于 s 2 s_2 s2 长度为 3 3 3 的前缀 ABA,字符串 A 既是其后缀也是其前缀,且是最长的,因此最长 border 长度为 1 1 1。
数据规模与约定
本题采用多测试点捆绑测试,共有 3 个子任务。
- Subtask 1(30 points): ∣ s 1 ∣ ≤ 15 |s_1| \leq 15 ∣s1∣≤15, ∣ s 2 ∣ ≤ 5 |s_2| \leq 5 ∣s2∣≤5。
- Subtask 2(40 points): ∣ s 1 ∣ ≤ 1 0 4 |s_1| \leq 10^4 ∣s1∣≤104, ∣ s 2 ∣ ≤ 1 0 2 |s_2| \leq 10^2 ∣s2∣≤102。
- Subtask 3(30 points):无特殊约定。
对于全部的测试点,保证 1 ≤ ∣ s 1 ∣ , ∣ s 2 ∣ ≤ 1 0 6 1 \leq |s_1|,|s_2| \leq 10^6 1≤∣s1∣,∣s2∣≤106, s 1 , s 2 s_1, s_2 s1,s2 中均只含大写英文字母。
思路
对模式串跑 KMP,得到 数组ne,然后直接扫文本串匹配即可,若失配则跳 ,完全匹配时也跳 ,因为有可能两次出现有重叠的部分。
AC代码
#include<bits/stdc++.h>
using namespace std;
const int N=1000010;
int n,m,i,j;
char p[N],s[N];
int ne[N];
int main(){scanf("%s%s",s+1,p+1);m=strlen(s+1);n=strlen(p+1);for(i=2,j=0;i<=n;i++){while(j&&p[i]!=p[j+1])j=ne[j];if(p[i]==p[j+1])j++;ne[i]=j;}for(i=1,j=0;i<=m;i++){while(j&&s[i]!=p[j+1])j=ne[j];if(s[i]==p[j+1])j++;if(j==n){printf("%d\n",i-n+1);j=ne[j];}}for(int i=1;i<=n;i++)printf("%d ",ne[i]);
}本质不同子串数
给定长度为 n n n的字符串 s ,求本质不同子串数。考虑用递推的方法,令 s,求本质不同子串数。 考虑用递推的方法,令 s,求本质不同子串数。考虑用递推的方法,令 f i f_i fi为 s [ 1 , i ] s[1,i] s[1,i]的本质不同子串数,考虑如何算出 f i + 1 f_{i+1} fi+1新出现的子串显然只能是以 i + 1 i+1 i+1结尾的。
如果将字符串反转,就变成要计数以 i + 1 i+1 i+1开头且未出现过的子串。
我们可以反过来计数已经出现过的有多少个,考虑我们前缀函数求出了什么,每一个border都是一个以 i + 1 i+1 i+1开头的子串的出现。
所以出现过的一共有 π m a x \pi_{max} πmax个,新增的就是 i + 1 − π m a x i+1-\pi_{max} i+1−πmax
这样我们就可以以 O ( 2 ) O(2) O(2)的复杂度求出本质不同子串数。
当然,还有更复杂的算法可以用更优秀的复杂度处理该问题,在此不表。
例题讲解
[NOI2014] 动物园
题目描述
近日,园长发现动物园中好吃懒做的动物越来越多了。例如企鹅,只会卖萌向游客要吃的。为了整治动物园的不良风气,让动物们凭自己的真才实学向游客要吃的,园长决定开设算法班,让动物们学习算法。
某天,园长给动物们讲解 KMP 算法。
园长:“对于一个字符串 S S S,它的长度为 L L L。我们可以在 O ( L ) O(L) O(L) 的时间内,求出一个名为 n e x t \mathrm{next} next 的数组。有谁预习了 n e x t \mathrm{next} next 数组的含义吗?”
熊猫:“对于字符串 S S S 的前 i i i 个字符构成的子串,既是它的后缀又是它的前缀的字符串中(它本身除外),最长的长度记作 n e x t [ i ] \mathrm{next}[i] next[i]。”
园长:“非常好!那你能举个例子吗?”
熊猫:“例 S S S 为 abcababc \verb!abcababc! abcababc,则 n e x t [ 5 ] = 2 \mathrm{next}[5]=2 next[5]=2。因为 S S S的前 5 5 5个字符为 abcab \verb!abcab! abcab, ab \verb!ab! ab 既是它的后缀又是它的前缀,并且找不到一个更长的字符串满足这个性质。同理,还可得出 n e x t [ 1 ] = n e x t [ 2 ] = n e x t [ 3 ] = 0 \mathrm{next}[1] = \mathrm{next}[2] = \mathrm{next}[3] = 0 next[1]=next[2]=next[3]=0, n e x t [ 4 ] = n e x t [ 6 ] = 1 \mathrm{next}[4] = \mathrm{next}[6] = 1 next[4]=next[6]=1, n e x t [ 7 ] = 2 \mathrm{next}[7] = 2 next[7]=2, n e x t [ 8 ] = 3 \mathrm{next}[8] = 3 next[8]=3。”
园长表扬了认真预习的熊猫同学。随后,他详细讲解了如何在 O ( L ) O(L) O(L) 的时间内求出 n e x t \mathrm{next} next 数组。
下课前,园长提出了一个问题:“KMP 算法只能求出 n e x t \mathrm{next} next 数组。我现在希望求出一个更强大 n u m \mathrm{num} num 数组一一对于字符串 S S S 的前 i i i 个字符构成的子串,既是它的后缀同时又是它的前缀,并且该后缀与该前缀不重叠,将这种字符串的数量记作 n u m [ i ] \mathrm{num}[i] num[i]。例如 S S S 为 aaaaa \verb!aaaaa! aaaaa,则 n u m [ 4 ] = 2 \mathrm{num}[4] = 2 num[4]=2。这是因为 S S S的前 4 4 4 个字符为 aaaa \verb!aaaa! aaaa,其中 a \verb!a! a 和 aa \verb!aa! aa 都满足性质‘既是后缀又是前缀’,同时保证这个后缀与这个前缀不重叠。而 aaa \verb!aaa! aaa 虽然满足性质‘既是后缀又是前缀’,但遗憾的是这个后缀与这个前缀重叠了,所以不能计算在内。同理, n u m [ 1 ] = 0 , n u m [ 2 ] = n u m [ 3 ] = 1 , n u m [ 5 ] = 2 \mathrm{num}[1] = 0,\mathrm{num}[2] = \mathrm{num}[3] = 1,\mathrm{num}[5] = 2 num[1]=0,num[2]=num[3]=1,num[5]=2。”
最后,园长给出了奖励条件,第一个做对的同学奖励巧克力一盒。听了这句话,睡了一节课的企鹅立刻就醒过来了!但企鹅并不会做这道题,于是向参观动物园的你寻求帮助。你能否帮助企鹅写一个程序求出 n u m \mathrm{num} num数组呢?
特别地,为了避免大量的输出,你不需要输出 n u m [ i ] \mathrm{num}[i] num[i] 分别是多少,你只需要输出所有 ( n u m [ i ] + 1 ) (\mathrm{num}[i]+1) (num[i]+1) 的乘积,对 1 0 9 + 7 10^9 + 7 109+7 取模的结果即可。
输入格式
第 1 1 1 行仅包含一个正整数 n n n,表示测试数据的组数。
随后 n n n 行,每行描述一组测试数据。每组测试数据仅含有一个字符串 S S S, S S S 的定义详见题目描述。数据保证 S S S 中仅含小写字母。输入文件中不会包含多余的空行,行末不会存在多余的空格。
输出格式
包含 n n n 行,每行描述一组测试数据的答案,答案的顺序应与输入数据的顺序保持一致。对于每组测试数据,仅需要输出一个整数,表示这组测试数据的答案对 1 0 9 + 7 10^9+7 109+7 取模的结果。输出文件中不应包含多余的空行。
样例 #1
样例输入 #1
3
aaaaa
ab
abcababc
样例输出 #1
36
1
32
提示
| 测试点编号 | 约定 |
|---|---|
| 1 | n ≤ 5 , L ≤ 50 n \le 5, L \le 50 n≤5,L≤50 |
| 2 | n ≤ 5 , L ≤ 200 n \le 5, L \le 200 n≤5,L≤200 |
| 3 | n ≤ 5 , L ≤ 200 n \le 5, L \le 200 n≤5,L≤200 |
| 4 | n ≤ 5 , L ≤ 10 , 000 n \le 5, L \le 10,000 n≤5,L≤10,000 |
| 5 | n ≤ 5 , L ≤ 10 , 000 n \le 5, L \le 10,000 n≤5,L≤10,000 |
| 6 | n ≤ 5 , L ≤ 100 , 000 n \le 5, L \le 100,000 n≤5,L≤100,000 |
| 7 | n ≤ 5 , L ≤ 200 , 000 n \le 5, L \le 200,000 n≤5,L≤200,000 |
| 8 | n ≤ 5 , L ≤ 500 , 000 n \le 5, L \le 500,000 n≤5,L≤500,000 |
| 9 | n ≤ 5 , L ≤ 1 , 000 , 000 n \le 5, L \le 1,000,000 n≤5,L≤1,000,000 |
| 10 | n ≤ 5 , L ≤ 1 , 000 , 000 n \le 5, L \le 1,000,000 n≤5,L≤1,000,000 |
思路
要求的就是每个前缀的 border 集合大小,并且满足这个 border 得是不大于字符串长度一半的。
首先给出一种暴力的做法,对于每一个前缀 s [ 1 : j ] s[1:j] s[1:j]都不断跳 next 指针,如果当前跳到 i i i的节点 满足其长度不超过 j 2 \frac{j}{2} 2j 那么就给 n u m j num_j numj加上1 。这个算法成立的原因是 border 的传递性:不断迭代 next 等价于遍历 border。
集合大小可以通过跳 next 的次数得到,也就是说我们可以记录一下从每个串出发不断跳next,能跳多少次,计为 c n t i cnt_i cnti ,那么有 c n t i = c n t n e x t i + 1 cnt_i=cnt_{next_i}+1 cnti=cntnexti+1 。其实也可以将 ( i , n e x t i ) (i,next_i) (i,nexti)建成一棵树,这棵树常被称为 b o r d e r border border树或是$ f a i l fail fail树。树上的深度也就代表着对应节点的 b o r d e r border border个数。
于是问题可以转化为对于每个 s [ 1 : i ] s[1:i] s[1:i]求满足条件的最长的 border s[1;j],之后给答案累乘上 c n t j + 1 cnt_j+1 cntj+1即可。
至于如何去求这个 j j j,首先给出一种基于分析的做法:
如果我们已经求出了 s [ 1 : i ] s[1 : i] s[1:i] 的 j j j ,在这个基础上去求 s [ 1 : i + 1 ] s[1 : i + 1] s[1:i+1] 的满足条件的 k k k 。
直觉告诉我们,用与求 next 指针一样的方法去做就好了:不断去检查 s j + 1 s_{j+1} sj+1 是否与 s i + 1 s_{i+1} si+1相等。如果是那么 k = j + 1 k = j + 1 k=j+1,否则令 j = n e x t j j = next_j j=nextj并继续检测相等的过程。特别的,
最终如果发现 k > i + 1 2 k > \frac{i+1}{2} k>2i+1,那么令 k = n e x t k k = next_k k=nextk。
根据与求 next 过程类似的分析可以发现,这个过程求出的 j 一定是一个合法的 border。
但是为什么一定是最大的?可以通过反证法证明,直接理解也并不困难。
另外给出一种看起来就很套路的做法:
问题可以转换到 border 树上。那么只需要对于每个前缀s[1 : i]求出border 树上 i 的祖先中长度满足条件 < i 2 <\frac{i}{2} <2i 的第一个并给答案累乘它的深度。
可以通过倍增来求解。预处理出 N e x t x , i Next_{x,i} Nextx,i表示从s[1 : x]跳 2 i 2^i 2i次 next 指针会跳到哪个节点。
对于每次询问i从大到小枚举二进制位,如果跳完之后还不满足 < i 2 <\frac{i}{2} <2i 就不断跳。这个过程与倍增求 lca 类似。
AC代码
#include <bits/stdc++.h>
using namespace std;
const int mod = 1e9 + 7;
char s[1000100];
int f[1000100], num[1000100];
int main() {int T;scanf("%d", &T);while (T--) {scanf("%s", s + 1);int n = strlen(s + 1);f[1] = 0;num[1] = 1;for (int i = 2, j = 0; i <= n; ++i) { while (j && s[j + 1] != s[i]) j = f[j];if (s[j + 1] == s[i])f[i] = ++j;elsef[i] = 0;num[i] = num[j] + 1;}long long ans = 1;for (int i = 2, j = 0; i <= n; ++i) {while (j && s[j + 1] != s[i]) j = f[j];if (s[j + 1] == s[i]) ++j;if (j > i >> 1) j = f[j];ans = (ans * (num[j] + 1)) % mod;}printf("%lld\n", ans);}return 0;
}[POI2006] OKR-Periods of Words
题面翻译
对于一个仅含小写字母的字符串 a a a, p p p 为 a a a 的前缀且 p ≠ a p\ne a p=a,那么我们称 p p p 为 a a a 的 proper 前缀。
规定字符串 Q Q Q 表示 a a a 的周期,当且仅当 Q Q Q 是 a a a 的 proper 前缀且 a a a 是 Q + Q Q+Q Q+Q 的前缀。若这样的字符串不存在,则 a a a 的周期为空串。
例如 ab 是 abab 的一个周期,因为 ab 是 abab 的 proper 前缀,且 abab 是 ab+ab 的前缀。
求给定字符串所有前缀的最大周期长度之和。
题目描述
A string is a finite sequence of lower-case (non-capital) letters of the English alphabet. Particularly, it may be an empty sequence, i.e. a sequence of 0 letters. By A=BC we denotes that A is a string obtained by concatenation (joining by writing one immediately after another, i.e. without any space, etc.) of the strings B and C (in this order). A string P is a prefix of the string !, if there is a string B, that A=PB. In other words, prefixes of A are the initial fragments of A. In addition, if P!=A and P is not an empty string, we say, that P is a proper prefix of A.
A string Q is a period of Q, if Q is a proper prefix of A and A is a prefix (not necessarily a proper one) of the string QQ. For example, the strings abab and ababab are both periods of the string abababa. The maximum period of a string A is the longest of its periods or the empty string, if A doesn’t have any period. For example, the maximum period of ababab is abab. The maximum period of abc is the empty string.
Task Write a programme that:
reads from the standard input the string’s length and the string itself,calculates the sum of lengths of maximum periods of all its prefixes,writes the result to the standard output.
输入格式
In the first line of the standard input there is one integer k k k ( 1 ≤ k ≤ 1 000 000 1\le k\le 1\ 000\ 000 1≤k≤1 000 000) - the length of the string. In the following line a sequence of exactly k k k lower-case letters of the English alphabet is written - the string.
输出格式
In the first and only line of the standard output your programme should write an integer - the sum of lengths of maximum periods of all prefixes of the string given in the input.
样例 #1
样例输入 #1
8
babababa
样例输出 #1
24
思路
根据 border 与周期的关系,我们知道我们要求的就是每个前缀的最小 border。
对于S[1 : i] ,如果其最小的 border j满足 i − j ≥ i 2 i-j\geq \frac{i}{2} i−j≥2i ,就可以为答案累计 。
根据迭代 next 遍历 border 集合的原理,我们可以对每个前缀s[1 : i]维护一个 m n i mn_i mni表示由i不断跳 next 所能得到的最小的非 0 border。
容易发现如果 n e x t i = 0 next_i=0 nexti=0,那么 m n i = i mn_i=i mni=i ,否则 m n i = m n n e x t i mn_i=mn_{next_i} mni=mnnexti 。
另外如果把本题放到 border 树上,可以发现这个要求的东西就是每个节点属于根节点(长度为 0 的前缀)的哪个子树。
AC代码
#include<bits/stdc++.h>
using namespace std;
const int N=1000010;
long long n,i,j;
char s[N];
long long ne[N],ans;
int main(){scanf("%d%s",&n,s+1);for(i=2,j=0;i<=n;i++){while(j&&s[i]!=s[j+1])j=ne[j];if(s[i]==s[j+1])j++;ne[i]=j;}for(i=2,j=2;i<=n;i++,j=i){while(ne[j])j=ne[j];if(ne[i])ne[i]=j;ans+=i-j;}cout<<ans<<endl;
}[BOI2009] Radio Transmission 无线传输
题目描述
给你一个字符串 s 1 s_1 s1,它是由某个字符串 s 2 s_2 s2 不断自我连接形成的(保证至少重复 2 2 2 次)。但是字符串 s 2 s_2 s2 是不确定的,现在只想知道它的最短长度是多少。
输入格式
第一行一个整数 L L L,表示给出字符串的长度。
第二行给出字符串 s 1 s_1 s1 的一个子串,全由小写字母组成。
输出格式
仅一行,表示 s 2 s_2 s2 的最短长度。
样例 #1
样例输入 #1
8
cabcabca
样例输出 #1
3
提示
样例输入输出 1 解释
对于样例,我们可以利用 abc \texttt{abc} abc 不断自我连接得到 abcabcabcabc \texttt{abcabcabcabc} abcabcabcabc,读入的 cabcabca \texttt{cabcabca} cabcabca,是它的子串。
规模与约定
对于全部的测试点,保证 1 < L ≤ 1 0 6 1 < L \le 10^6 1<L≤106。
思路
本题考查的是对next数组的理解,其实答案就是n-ne[n]
AC代码
#include<bits/stdc++.h>
using namespace std;
const int N=1000010;
int n,m,i,j;
char p[N],s[N];
int ne[N];
int main(){scanf("%d%s",&n,p+1);for(i=2,j=0;i<=n;i++){while(j&&p[i]!=p[j+1])j=ne[j];if(p[i]==p[j+1])j++;ne[i]=j;}printf("%d\n",n-ne[n]);
}[COCI2011-2012#4] KRIPTOGRAM
题目描述
现有一段明文和一部分密文。明文和密文都由英文单词组成,且密文中的一个单词必然对应着明文中的一个单词。
求给出的密文在明文中可能出现的最早位置。
输入格式
第一行,若干个英文单词和一个 $\texttt $$,表示明文。
第二行,若干个英文单词和一个 $\texttt $$,表示密文。
每行末尾的 $\texttt $$ 用于表示该行结束。数据保证没有多个 $\texttt $$ 出现在同一行的情况。
输出格式
输出密文在明文中可能出现的最早位置,即密文的第一个单词在明文中可能出现的最早位置。
样例 #1
样例输入 #1
a a a b c d a b c $
x y $
样例输出 #1
3
样例 #2
样例输入 #2
xyz abc abc xyz $
abc abc $
样例输出 #2
2
样例 #3
样例输入 #3
a b c x c z z a b c $
prvi dr prvi tr tr x $
样例输出 #3
3
提示
【数据规模与约定】
- 对于 100 % 100\% 100% 的数据,明文和密文所对应字符串的长度不超过 1 0 6 10^6 106,输入的单词均由小写字母组成。
【提示与说明】
题目译自 COCI 2011-2012 CONTEST #4 Task 6 KRIPTOGRAM。
本题分值按 COCI 原题设置,满分 140 140 140。
思路
在传统的 KMP 算法中,我们直接比较字符之间是否相等。
针对此题的情况,只需要把判断式换成i - preA[i]== j - preB[j] || ! preB[j] && preA[i] <= i - j就行
AC代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
string a[N], b[N];
int lena, lenb;
int sp_len[N], prea[N], preb[N];
void getPre(string str[], int pre[], int length) {unordered_map<string, int> last_pos;for (int i=1;i<=length;i++) {pre[i]=last_pos[str[i]];last_pos[str[i]]=i;}
}
void getSpLen() {int i=2,j=1;while (i<=lenb) {if(i-preb[i]==j-preb[j]||!preb[j]&&preb[i]<=i-j)sp_len[i++]=j++;else if(j>1)j=sp_len[j-1]+1;else i++;}
}
int main() {string x;while (cin>>x,x!="$")a[++lena]=x;while (cin>>x,x!="$")b[++lenb]=x;getPre(a,prea,lena);getPre(b,preb,lenb);getSpLen();int i=1,j=1;while (i<=lena) {if(i-prea[i]==j-preb[j]||!preb[j]&&prea[i]<=i-j)i++, j++;else if(j>1)j=sp_len[j-1]+1;else i++;if(j>lenb){cout<<i-lenb<<endl;return 0;}}cout<<-1<<endl;return 0;
}
这是我的第十九篇文章,如有纰漏也请各位大佬指正
辛苦创作不易,还望看官点赞收藏打赏,后续还会更新新的内容。
相关文章:

浅谈KMP算法(c++)
目录 前缀函数应用【模板】KMP题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 提示样例 1 解释数据规模与约定 思路AC代码 本质不同子串数 例题讲解[NOI2014] 动物园题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 提示思路AC代码 [POI2006] OKR-Periods of …...
关于C++编程注意点(竞赛)
赛前准备 多复习 重中之重, 多刷题 确保手感 参加几场模拟赛,熟悉流程 熟悉 Linux 系统,否则你将会手忙脚乱 放松心情,调整心态,分数 实力 心态 赛中注意 输入输出方面 在数据范围超过 时尽量使用 scanf pr…...
Markdown文本编辑器:Typora for Mac/win 中文版
Markdown 是一种轻量级的标记语言,它允许用户使用易读易写的纯文本格式编写文档。Typora 支持且仅支持 Markdown 语法的文本编辑,生成的文档后缀名为 .md。 这款软件的特点包括: 实时预览:Typora 的一个显著特点是实时预览&#x…...

Mysql-窗口函数一
文章目录 1. 窗口函数概述1.1 介绍1.2 作用 2. 场景说明2.1 准备工作2.2 场景说明2.3 分析2.4 实现2.4.1 非窗口函数方式实现2.4.2 窗口函数方式实现 3. 窗口函数分类4. 窗口函数基础用法:OVER关键字4.1 语法4.2 场景一 :计算每个值和整体平均值的差值4.2.1 需求4.2…...

Python3 爬虫 数据抓包
一、数据抓包 所谓抓包(Package Capture),简单来说,就是在网络数据传输的过程中对数据包进行截获、查看、修改或转发的过程。如果把网络上发送与接收的数据包理解为快递包裹,那么在快递运输的过程中查看里面的内容&…...

js强制刷新
在JavaScript中触发强制刷新通常指的是强制浏览器重新加载页面,忽略缓存。以下是几种实现强制刷新的方法: ### 使用 location.reload() 这是最简单的方法,它会重新加载当前页面。 javascript location.reload(true); // 传入true参数表示强制…...

yolov5 part2
two-stage (两阶段):Faster-rcnn Mask-Rcnn系列 one-stage (单阶段):YOLO系列 最核心的优势:速度非常快,适合实时监测任务。但是缺点也有,效果可能不好 速度较慢在2018…...

Hive3:表操作常用语句-内部表、外部表
一、内部表 1、基本介绍 (CREATE TABLE table_name ......) 未被external关键字修饰的即是内部表, 即普通表。 内部表又称管理表,内部表数据存储的位置由hive.metastore.warehouse.dir参数决定(默认:/user/hive/ware…...

【PXE+kickstart】linux网络服务之自动装机
PXE: 简介:PXE(Preboot execute environment 是一种能够让计算机通过网络启动的引导方式,只要网卡支持PXE协议即可使用Kickstart 是一种无人值守的安装方式,工作原理就是预先把原本需要运维人员手工填写的参数保存成一个 ks.cfg 文…...

vmware ubuntu虚拟机网络联网配置
介绍vmware虚拟机配置基础网络环境,同时连接外网(通过桥接模式),以及ubuntu下输入法等基础工具安装。 本文基于ubuntu22.04,前提虚拟机已经完成安装。本文更多是针对vmware虚拟机的设置,之前有一篇针对ubun…...

Vue3_对接声网实时音视频_多人视频会议
目录 一、声网 1.注册账号 2.新建项目 二、实时音视频集成 1.声网CDN集成 2.iframe嵌入html 3.自定义UI集成 4.提高进入房间速度 web项目需要实现一个多人会议,对接的声网的灵动课堂。在这里说一下对接流程。 一、声网 声网成立于2014年,是全球…...

慧灵科技:创新引领自动化未来
在智能制造与自动化生产日益成为主流趋势的今天,慧灵科技凭借其卓越的技术创新能力和产品优势,在机器人领域崭露头角。 自2015年在深圳成立以来,慧灵科技专注于核心技术的研发与产品创新,为各行业提供性价比极高的机器人产品及自…...

【TiDB 社区智慧合集】TiDB 在核心场景的实战应用
作者: 社区小助手 原文来源: https://tidb.net/blog/5cc4ec70 杭州银行 杭州银行采用 TiDB 作为其核心系统数据库,标志着银行资产规模和业务复杂性的大幅增长。通过"分布式透明化"的思考,杭州银行实现了从传统 Orac…...

JetBrains:XML tag has empty body警告
在xml文件中配置时,因为标签内容为空,出现黄色警告影响观感。 通过IDE配置关闭告警...
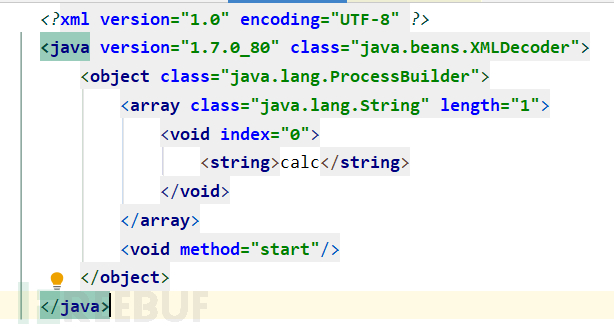
XMLDecoder反序列化
XMLDecoder反序列化 基础知识 就简单讲讲吧,就是为了解析xml内容的 一般我们的xml都是标签属性这样的写法 比如person对象以xml的形式存储在文件中 在decode反序列化方法后,控制台成功打印出反序列化的对象。 就是可以根据我们的标签识别是什么成分…...

C# 高级数据处理:深入解析数据分区 Join 与 GroupJoin 操作的应用与实例演示
文章目录 一、概述二. 数据分区 (Partitioning)三、Join 操作符1. Join 操作符的基本用法2. Join 操作符示例 四、GroupJoin 操作符1. GroupJoin 操作符的基本用法2. GroupJoin 操作符示例 总结 在数据处理中,联接(Join)操作是一种非常常见的…...

数据库典型例题2-ER图转换关系模型
1.question solution: 2.做题步骤 一些解释: <1弱实体把强属性的主键写进去,指向强属性。eg:E6_A13指向E5_A13 <21:1,1:n,m:n:将完全参与的一方(双线)指向另一方,并将对方的…...

Java:设计模式(单例,工厂,代理,命令,桥接,观察者)
模式是一条由三部分组成的通用规则:它代表了一个特定环境、一类问题和一个解决方案之间的关系。每一个模式描述了一个不断重复发生的问题,以及该问题解决方案的核心设计。 软件领域的设计模式定义:设计模式是对处于特定环境下,经常…...

【算法】KMP算法
应用场景 有一个字符串 str1 "BBA ABCA ABCDAB ABCDABD",和一个子串 str2 "ABCDABD"现在要判断 str1 是否含有 str2,如果含有,就返回第一次出现的位置,如果不含有,则返回 -1 我们很容易想到暴力…...

nginx续1:
八、虚拟主机配置 基于域名的虚拟主机 [rootserver2 ~]# ps -au|grep nginx //查看进程 修改Nginx服务配置,添加相关虚拟主机配置如下 1. [rootproxy ~]# vim /usr/local/nginx/conf/nginx.conf 2. .. .. 3. server { 4. listen …...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...
