力扣刷题之3143.正方形中的最多点数
题干描述
给你一个二维数组 points 和一个字符串 s ,其中 points[i] 表示第 i 个点的坐标,s[i] 表示第 i 个点的 标签 。
如果一个正方形的中心在 (0, 0) ,所有边都平行于坐标轴,且正方形内 不 存在标签相同的两个点,那么我们称这个正方形是 合法 的。
请你返回 合法 正方形中可以包含的 最多 点数。
注意:
- 如果一个点位于正方形的边上或者在边以内,则认为该点位于正方形内。
- 正方形的边长可以为零。
示例 1:

输入:points = [[2,2],[-1,-2],[-4,4],[-3,1],[3,-3]], s = "abdca"
输出:2
解释:
边长为 4 的正方形包含两个点 points[0] 和 points[1] 。
示例 2:

输入:points = [[1,1],[-2,-2],[-2,2]], s = "abb"
输出:1
解释:
边长为 2 的正方形包含 1 个点 points[0] 。
示例 3:
输入:points = [[1,1],[-1,-1],[2,-2]], s = "ccd"
输出:0
解释:
任何正方形都无法只包含 points[0] 和 points[1] 中的一个点,所以合法正方形中都不包含任何点。
题干分析
已知题目要求我们找到一个合法的正方形,中心在(0,0),边平行于坐标轴,并且正方形内不能有两个点的标签相同。我么需要返回这样一个合法正方形内可以包含的最多点。
示例分析
- 示例1:在标签a和b的最小距离都小于所有标签的次小距离的情况下,可以容纳最多的点数是2。
- 示例2:因为只有标签a的最小距离小于次小距离,所以结果是1.
- 示例3:所有点都无法单独构成合法的正方形,所以结果是0。
解题思路
1.定义一个合法的正方形:
- 正方形的中心为(0,0)。
- 正方形的边长可以从0开始逐渐增加。
- 在正方形的边界或内部不能有两个标签相同的点。
2.距离计算:
计算每个点(x,y)到原点的最大绝对坐标距离,即d = max(abs(x),abs(y))。这样,边长为2*d的正方形可以刚好覆盖这个点。选择最大的绝对值是因为正方形的边需要平行于坐标轴,确保正方形能够完全包含点(x,y)。
3.最小距离更新:
我们维护一个min1数组和一个min2变量:
- min1数组:用于记录每个标签对应的最小距离。min1[j]表示标签为j的点中,到原点的最小距离。这个最小距离表示对于每个标签j,能使其位于正方形内的最小正方形边长。
- min2变量:用于记录所有标签中的次小最小距离。这意味着所有标签的最小距离中,第二小的值。这个值的意义在于如果某个标签的最小距离小于min2,我们就能够确保在正方形中只包含这一标签,而不包含其他可能导致标签冲突的点。换句话说,标签j的最小距离min1[j]小于min2以为着子在该标签的正方形内部不会有其他标签的点,也即不会有标签重复的情况。
4.判断合法性:
- 如果一个标签的最小距离min1[j]小于min2,则可以认为这个标签可以包含在合法正方形中。
- 这是因为min2是次小的最小距离,任何小于min2的标签距离都不会导致重复的标签出现。
5.最大化点数:
- 计算并返回所有满足条件的标签的数量,这个数量即是哈法正方形内可以包含的最多点数。
代码示例
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>//计算最大合法正方形的点数
int maxPointsInsideSquare(int** points, int pointsSize, int* pointsColSze, char* s) {int min1[26];//初始化每个标签的最小距离为最大值for (int i = 0; i < 26; i++){min1[i] = INT_MAX;}int min2 = INT_MAX;//第二小的最小距离初始化为最大值int n = pointsSize;//点的数量//遍历所有点for (int i = 0; i < n; ++i){int x = points[i][0], y = points[i][1];int j = s[i] - 'a';//标签对应的索引int d = (abs(x) > abs(y)) ? abs(x) : abs(y); // 计算该点到原点的距离//更新每个标签的最小和次小距离if (d < min1[j]){min2 = (min2 < min1[j]) ? min2 : min1[j];min1[j] = d;}else if (d < min2) {min2 = d;}}int res = 0;//用于记录最大合法点数//统计合法点数for (int i = 0; i < 26; i++){if (min1[i] < min2) {//如果标签的最小距离小于次小距离,则认为其可以包含在合法正方形中++res;//增加合法点数计数}}return res;//返回合法点数
}
int main() {// 测试用例1int points1[][2] = { {2, 2}, {-1, -2}, {-4, 4}, {-3, 1}, {3, -3} };int* ptr1[5];for (int i = 0; i < 5; i++) {ptr1[i] = points1[i];}int pointsColSize1[5] = { 2, 2, 2, 2, 2 }; // 每个点的列数char s1[] = "abdca"; // 标签字符串printf("Output: %d\n", maxPointsInsideSquare(ptr1, 5, pointsColSize1, s1)); // 期望输出: 2// 测试用例2int points2[][2] = { {1, 1}, {-2, -2}, {-2, 2} };int* ptr2[3];for (int i = 0; i < 3; i++) {ptr2[i] = points2[i];}int pointsColSize2[3] = { 2, 2, 2 }; // 每个点的列数char s2[] = "abb"; // 标签字符串printf("Output: %d\n", maxPointsInsideSquare(ptr2, 3, pointsColSize2, s2)); // 期望输出: 1// 测试用例3int points3[][2] = { {1, 1}, {-1, -1}, {2, -2} };int* ptr3[3];for (int i = 0; i < 3; i++) {ptr3[i] = points3[i];}int pointsColSize3[3] = { 2, 2, 2 }; // 每个点的列数char s3[] = "ccd"; // 标签字符串printf("Output: %d\n", maxPointsInsideSquare(ptr3, 3, pointsColSize3, s3)); // 期望输出: 0return 0;
}相关文章:

力扣刷题之3143.正方形中的最多点数
题干描述 给你一个二维数组 points 和一个字符串 s ,其中 points[i] 表示第 i 个点的坐标,s[i] 表示第 i 个点的 标签 。 如果一个正方形的中心在 (0, 0) ,所有边都平行于坐标轴,且正方形内 不 存在标签相同的两个点,…...
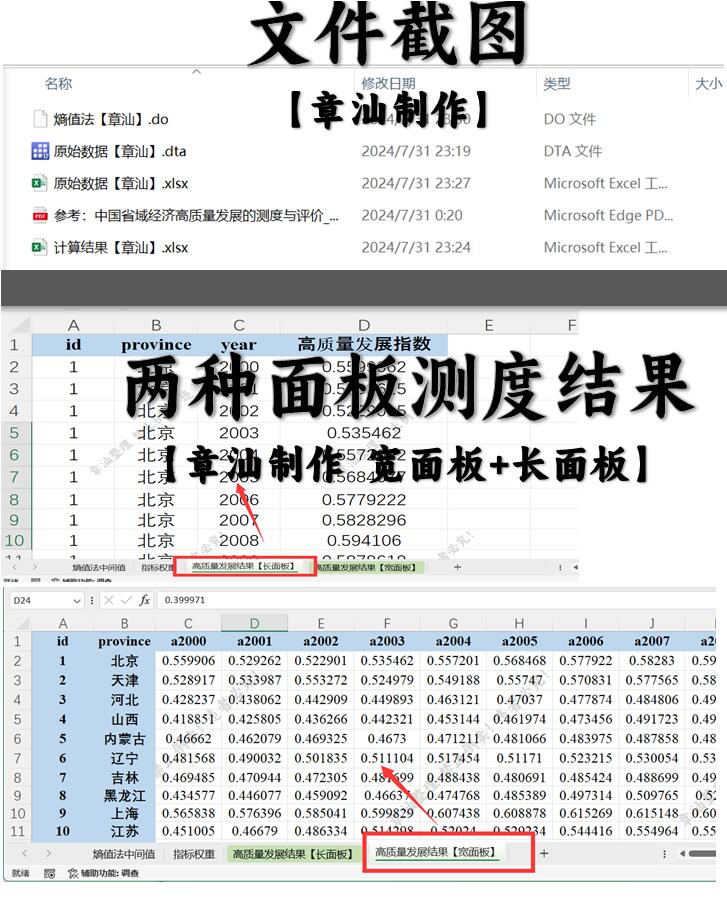
【更新2022】省级经济高质量发展指标体系测度 含代码 2000-2022
重磅更新!【章汕】制作“省级经济高质量发展指标体系测度 含代码”,市面上有这个版本的数据,但其内容非常不全面,个别指标有误,没有stata和代码,即使有代码小白也很容易报错;没有权重、宽面板等…...

缓冲流练习
练习1:拷贝文件 四种方式拷贝文件,并统计各自用时。 字节流的基本流:一次读写一个字节 字节流的基本流:一次读写一个字节数组 字节缓冲流:一次读写一个字节 字节缓冲流:一次读写一个字节数组 这里我只使用了…...

自己履行很多的话语,依旧按照这个方式进行生活
《明朝那些事儿》最后一段讲述了徐霞客的故事,作者当年明月通过徐霞客的生平表达了一种人生哲学。在书的结尾,当年明月写道:"成功只有一个——按照自己的方式,去度过人生",这句话被用作《明朝那些事儿》的结…...

交通预测数据文件梳理:METR-LA
文章目录 前言一、adj_METR-LA.pkl文件读取子文件1读取子文件2读取子文件3 二、METR-LA.h5文件 前言 最近做的实验比较多,对于交通预测数据的各种文件和文件中的数据格式理解愈加混乱,因此打算重新做一遍梳理来加深实验数据集的理解,本文章作…...

按钮类控件
目录 1.Push Button 代码示例: 带有图标的按钮 代码示例: 带有快捷键的按钮 代码示例: 按钮的重复触发 2.Radio Buttion 代码示例: 选择性别 代码示例: click, press, release, toggled 的区别 代码示例: 单选框分组 3.3 Check Box 代码示例: 获取复选按钮的取值 1.Pu…...

opencascade AIS_ViewController源码学习 视图控制、包含鼠标事件等
opencascade AIS_ViewController 前言 用于在GUI和渲染线程之间处理视图器事件的辅助结构。 该类实现了以下功能: 缓存存储用户输入状态(鼠标、触摸和键盘)。 将鼠标/多点触控输入映射到视图相机操作(平移、旋转、缩放࿰…...

拉削基础知识——拉床的类型及特点
拉床是所有机械加工工具中最简单的一种,由拉削工具、夹具、驱动装置和支撑架组成。拉削加工可获得较高的尺寸精度和较小的表面粗糙度,生产率较高,适用于大批量生产。拉床按其结构主要分为卧式和立式。应用领域和功能可分为液压拉床、自动拉床…...

docker-compose笔记
docker 目前docker官网已经无法登录,但是还可以从清华镜像站(https://mirrors.tuna.tsinghua.edu.cn/docker-ce/)下载。 使用方法可以参考早期文章《docker笔记》 docker-compose 可以从Github下载不同版本的二进制文件,例如do…...

C# 自定义控件无法加载
问题 在做winform开发时自己定义了一个控件,控件在工具箱中显示了,但是拖动到窗体设计器时会提示未能加载工具箱项xxx,将从工具箱中将其删除,如下图所示: 点击确定后,控件会从工具箱中移除。 解决方法 将 生成>…...

avl树自实现(带图),探讨平衡因子与旋转
引子: 在此之前,我们学过了搜索二叉树,这种树,在如果数据有序或接近有序的情况下,二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下,而且普通搜索二叉树无法有…...

Elasticsearch 的DSL查询,聚合查询与多维度数据统计
文章目录 搜索聚合高阶概念 搜索 即从一个索引下按照特定的字段或关键词搜索出符合用户预期的一个或者一堆cocument,然后根据文档的相关度得分,在返回的结果集里并根据得分对这些文档进行一定的排序。 聚合 根据业务需求,对文档中的某个或…...

【如何高效处理前端常见问题:策略与实践】
在快速发展的Web开发领域,前端作为用户与应用程序直接交互的界面,其重要性不言而喻。然而,随着技术的不断演进和项目的复杂化,前端开发者在日常工作中难免会遇到各种挑战和问题。本文旨在深入探讨前端开发中常见的问题类型&#x…...

聊聊前端 JavaScript 的扩展运算符 “...“ 的使用场景
前言 在 JavaScript 中,... 被称为 “扩展运算符” 或 “剩余参数运算符”。 扩展运算符是在 ES6(ECMAScript 2015)中被引入的,目的是为了提高语言的表达能力和代码的可读性。 根据上下文不同,它主要用在数组、对象…...

华为续签了,但我准备离职了
离职华为 今天在牛客网看到一篇帖子,名为《华为续签了,但我准备离职了》。 讲得挺真诚,可能也是一类毕业进华为的同学的心声。 贴主提到,当年自己还是应届毕业的时候,手握多个 offer,最终选的华为ÿ…...

RocketMQ 的认证与授权机制
Apache RocketMQ 是一个高性能、高吞吐量、分布式的消息中间件,广泛应用于异步通信、应用解耦、流量削峰等场景。在企业级应用中,消息安全尤为重要,本文将深入探讨 RocketMQ 的认证与授权机制,帮助开发者和系统管理员更好地理解和…...

【设计模式】六大原则-上
首先什么是设计模式? 相信刚上大学的你和我一样,在学习这门课的时候根本不了解这些设计原则和模式有什么用处,反而不如隔壁的C更有意思,至少还能弹出一个小黑框,给我个hello world。 如何你和我一样也是这么想…...

CRC16循环冗余校验
代码: #include<stdio.h> #include <stdint.h>#define uchar unsigned char #define uint unsigned int static const uint8_t auchCRCHi[] { 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x0…...

Mysql80主从复制搭建;遇到问题 Slave_IO_Running: Connecting和Slave_SQL_Running以及解决过程
总结主要步骤 1.配置一个提供复制的账号; 创建用户 CREATE USER replication% IDENTIFIED BY your_password; GRANT REPLICATION SLAVE ON *.* TO replication%; FLUSH PRIVILEGES;2.修改配置 选择模式 主库配置; windows的得话是my.ini文件 默认这个目…...

Yarn网络代理配置指南:在受限网络环境中优化依赖管理
Yarn是一个现代的包管理器,用于JavaScript项目,它提供了快速、可靠和安全的依赖管理方式。然而,在某些受限的网络环境中,例如公司内网或某些国家地区,直接连接到公共npm仓库可能不可行或效率低下。这时,配置…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...

【前端实战】如何让用户回到上次阅读的位置?
目录 【前端实战】如何让用户回到上次阅读的位置? 一、总体思路 1、核心目标 2、涉及到的技术 二、实现方案详解 1、基础方法:监听滚动,记录 scrollTop(不推荐) 2、Intersection Observer 插入探针元素 3、基…...

数据库优化实战指南:提升性能的黄金法则
在现代软件系统中,数据库性能直接影响应用的响应速度和用户体验。面对数据量激增、访问压力增大,数据库性能瓶颈经常成为项目痛点。如何科学有效地优化数据库,提升查询效率和系统稳定性,是每位开发与运维人员必备的技能。 本文结…...
