奇偶函数的性质及运算
目录
定义
注意
特征
运算
拓展
定义
设函数f(x)的定义域D;
- 如果对于函数定义域D内的任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数。
- 如果对于函数定义域D内的任意一个x,都有f(-x)=f(x),那么函数f(x)就叫做偶函数。
- 如果对于函数定义域D内的任意一个x,f(-x)=-f(x)与f(-x)=f(x)同时成立,那么函数f(x)既是奇函数又是偶函数,称为既奇又偶函数。
- 如果对于函数定义域内的任意一个x,f(-x)=-f(x)或f(-x)=f(x)都不能成立,那么函数f(x)既不是奇函数又不是偶函数,称为非奇非偶函数。
注意
①奇、偶性是函数的整体性质,对整个定义域而言。
②奇、偶函数的定义域一定关于原点对称,如果一个函数的定义域不关于原点对称,则这个函数一定不是奇(或偶)函数。
③判断或证明函数是否具有奇偶性的根据是定义、变式。
变式:
奇:f(x)+f(-x)=0; f(x)*f(-x) = -f^2(x); f(x)/f(-x) = -1.
偶:f(x)-f(-x) = 0; f(x)*f(-x) = f^2(x); f(x)/f(-x) = 1.
特征
定理:奇函数的图像关于原点成中心对称图形,偶函数的图象关于y轴对称。
推论:
- 如果对于任一个x,都有f(a+x)+f(b-x)=c,那么函数图像关于(a/2+b/2,c/2)中心对称;
- 如果对于任意一个x,有f(a+x)=f(a-x),那么函数图像关于x=a轴对称。
奇函数的图像关于原点对称 —— 点(x,y)→(-x,-y)
偶函数的图像关于y轴对称 —— 点(x,y)→(-x,y)
奇函数在某一区间上单调递增,则在它的对称区间上也是单调递增。
偶函数在某一区间上单调递增,则在它的对称区间上单调递减。
运算
- 两个偶函数相加所得的和为偶函数。
- 两个奇函数相加所得的和为奇函数。
- 两个偶函数相乘所得的积为偶函数。
- 两个奇函数相乘所得的积为偶函数。
- 一个偶函数与一个奇函数相乘所得的积为奇函数。
- 几个函数复合,只要有一个是偶函数,结果是偶函数;若无偶函数则是奇函数。
- 偶函数的和差积商是偶函数。
- 奇函数的和差是奇函数。
- 奇函数的偶数个积商是偶函数。
- 奇函数的奇数个积商是奇函数。
- 奇函数的绝对值为偶函数。
- 偶函数的绝对值为偶函数。
拓展
(1)设f(x)可导,则
- f(x)是奇函数---->f'(x)是偶函数
- f(x)是偶函数---->f'(x)是奇函数
(2)连续的奇函数其原函数都是偶函数;
连续的偶函数其原函数中有且仅有一个是奇函数。
(3)设f(x)连续
- 若f(x)是奇函数,则
是偶函数;
- 若f(x)是偶函数,则
是奇函数。
相关文章:
奇偶函数的性质及运算
目录 定义 注意 特征 运算 拓展 定义 设函数f(x)的定义域D; 如果对于函数定义域D内的任意一个x,都有f(-x)-f(x),那么函数f(x)就叫做奇函数。如果对于函数定义域D内的任意一个x…...
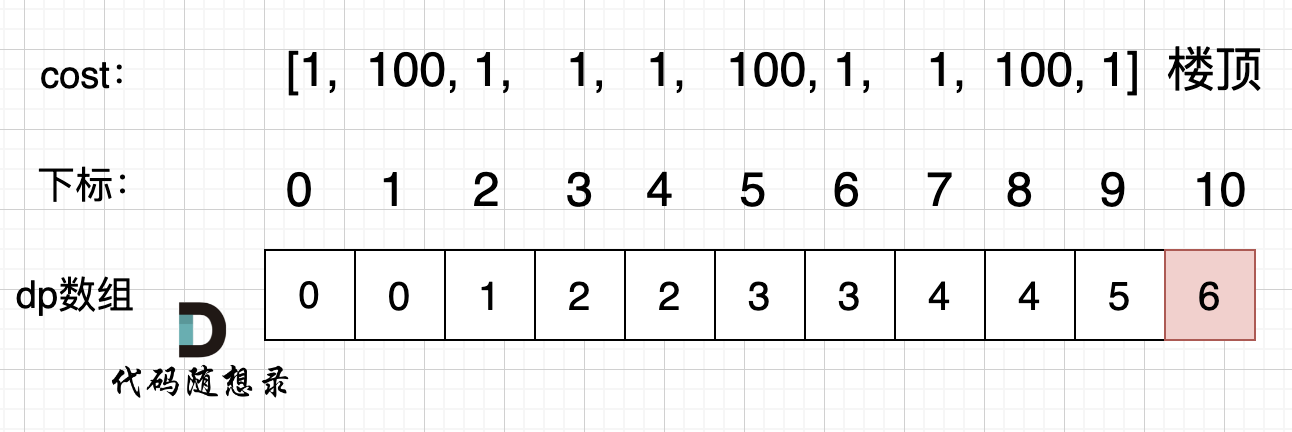
代码随想录 day 32 动态规划
第九章 动态规划part01 今天正式开始动态规划! 理论基础 无论大家之前对动态规划学到什么程度,一定要先看 我讲的 动态规划理论基础。 如果没做过动态规划的题目,看我讲的理论基础,会有感觉 是不是简单题想复杂了? …...

支持目标检测的框架有哪些
目标检测是计算机视觉领域的一个重要任务,许多深度学习框架都提供了对目标检测的支持。以下是一些广泛使用的支持目标检测的深度学习框架: 1. TensorFlow TensorFlow 是一个广泛使用的开源深度学习框架,由Google开发。它提供了TensorFlow O…...

原神自定义倒计时
<!DOCTYPE html> <html lang"zh-CN"><head><meta charset"UTF-8"><title>原神倒计时</title><style>* {margin: 0;padding: 0;box-sizing: border-box;user-select: none;body {background: #0b1b2c;}}header {…...

top命令实时监测Linux进程
top命令可以动态实时显示Linux进程信息,方便观察频繁换进换出的内存的进程变化。 top命令执行示例如下: 其中,第一行表示系统当前时间、系统的运行时间、登录的用户数目、系统的平均负载(最近1分钟,最近5分钟ÿ…...

Rust 所有权
所有权 Rust的核心特性就是所有权所有程序在运行时都必须管理他们使用计算机内存的方式 有些语言有垃圾收集机制,在程序运行时,他们会不断地寻找不再使用的内存在其他语言中,程序员必须显式的分配和释放内存 Rust采用了第三种方式࿱…...

Python面试题:结合Python技术,如何使用PyTorch进行动态计算图构建
PyTorch 是一个流行的深度学习框架,它通过动态计算图(Dynamic Computation Graphs)来支持自动微分(Autograd)。动态计算图的特点是每次前向传播时都会构建新的计算图,这使得它非常灵活,适合处理…...

基于RHEL7的服务器批量安装
目录 一、项目要求 二、实验环境 三、生成kickstart自动化安装脚本 四、搭建dhcp服务并测试kickstart脚本 五、搭建pxe网络安装环境实现服务器自动部署 编辑 六、测试 一、项目要求 1.使用kickstart编写自动化安装脚本 2.搭建dhcp服务并测试kickstart脚本 3.搭建px…...

C. Light Switches
文章目录 C. Light Switches题意:解题思路:解题代码: C. Light Switches 原题链接 题意: 房间的灯最初均为关闭状态,安装芯片后,它会每隔k分钟改变一次房间的灯光状态,即会打开灯光k分钟&…...

LabVIEW机器人神经网络运动控制系统
LabVIEW机器人神经网络运动控制系统 介绍了如何使用LabVIEW软件和中枢模式发生器(CPG)神经网络实现对舵机驱动爬壁机器人的精准运动控制。通过结合仿生控制理念与高级程序设计,本项目旨在开发一种能自动完成复杂墙面移动任务的机器人。 项目背景 现代机器人技术中…...

Qt WebEngine播放DRM音视频
Qt WebEngine播放DRM受保护视频,前提是Qt WebEngine开启音视频编码器,能够支持网页上普通视频的播放。开启音视频编码器需要自己编译源码,这里不做介绍。 什么是DRM音视频 DRM视频是指数字版权管理(Digital Rights Management&a…...

渗透小游戏,各个关卡的渗透实例
Less-1 首先,可以看见该界面,该关卡主要是SQL注入,由于对用户的输入没有做过滤,使查询语句进入到了数据库中,查询到了本不应该查询到的数据 首先,如果想要进入内部,就要绕过,首先是用…...

SpringBoot集成阿里百炼大模型(初始demo) 原子的学习日记Day01
文章目录 概要下一章SpringBoot集成阿里百炼大模型(多轮对话) 原子的学习日记Day02 整体架构流程技术名词解释集成步骤1,选择大模型以及获取自己的api-key(前面还有一步开通服务就没有展示啦!)2,…...

高级java每日一道面试题-2024年8月06日-web篇-cookie,session,token有什么区别?
如果有遗漏,评论区告诉我进行补充 面试官: cookie,session,token有什么区别? 我回答: 在Web开发中,cookie、session和token是三种常见的用于用户身份验证和会话管理的技术。它们各自有不同的用途和优缺点,下面将详细解释: 1. Cookie 定…...

Python 图文:小白也能轻松生成精美 PDF 报告!
摘要: 还在为枯燥的数据报表发愁吗?想让你的 Python 项目报告瞬间高大上?本文将带你学习如何使用 Python 生成图文并茂的 PDF 文件,从此告别单调,让你的数据“活”起来! 一、 引言 想象一下,你正在为公司…...
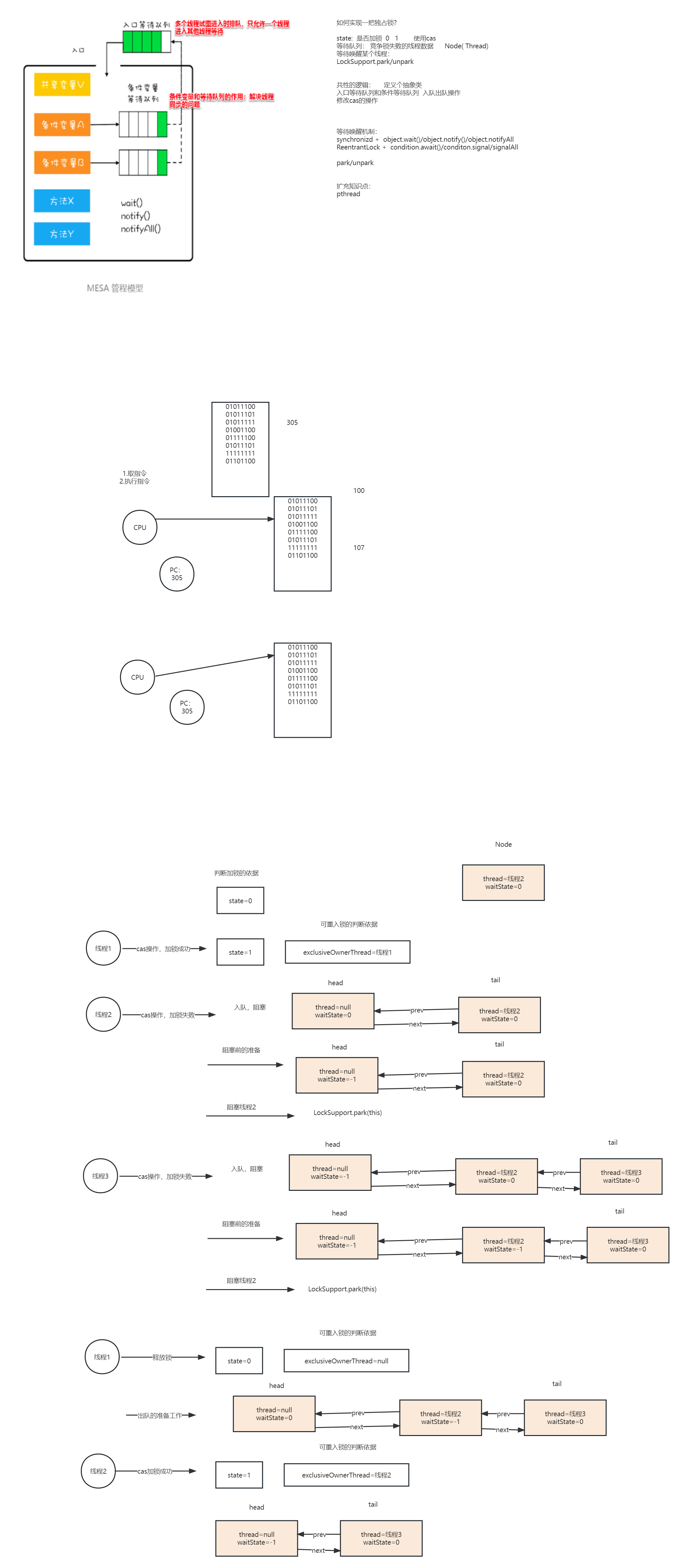
AQS的ReentrantLock源码
什么是AQS(全称AbstractQueuedSynchronizer) 代表:重入锁、独占锁/共享锁、公平锁/非公平锁 是JUC包中线程阻塞、阻塞队列、唤醒、尝试获取锁的一个框架 AbstractQueuedSynchronizer是全称,是一个模板模式,一些线程…...

CSP-J 模拟题2
如果x大于45,则输出-1 设定一个整数now,他的初始值为9; 当x>now,就x-now,并且now--; 根据解析写代码1: #include <bits/stdc.h> using namespace std; int a[101010]; int main(){int x;cin>…...

途牛养车省养车平台源码 买卖新车租车二手车维修装潢共享O2O程序源码
源码采用FastAdmin框架开发,功能成熟完善,已有成功案例。 业务涵盖保险、二手车、接送、拖车、租车、保养、维修、入驻等连接线上等基础和深度服务。 采用的是“线上 车主直控社区加盟店” 模式,其主要考虑是布局门店有助于让目标消费用户…...

开发中遇到的gzuncompress,DomDocument等几个小问题以及一次Php上线碰到的502问题及php异常追踪
一、开发中遇到的gzuncompress,DomDocument等几个小问题记在此 1,昨天在命令行模式行运行一个很复杂的程序,一开始执行php,刚刚连接数据库,都没怎么查几条记录,(publish:October 27, 2017 -Fridayÿ…...

【Material-UI】Button 组件中的基本按钮详解
文章目录 一、基本按钮变体1. 文本按钮(Text Button)2. 实心按钮(Contained Button)3. 轮廓按钮(Outlined Button) 二、应用场景与注意事项1. 使用场景2. 注意事项 三、总结 Material-UI 的 Button 组件是前…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
