C++ 几何算法 - 向量点乘,叉乘及其应用
一:点乘介绍
1. 向量点乘:

2. 向量点乘的性质:

3. 向量点乘公式:



4. 向量的点乘的属性:
(1):向量与自身做点乘,会得到向量长度的平方:![]()
(2):向量长度,为向量与自身点乘后再求平方根:![]()
(3):向量投影,将a向量投影到向量b上:
(4):向量夹角:
二:叉乘介绍:
1. 向量叉乘:

2. 向量叉乘公式:

3. 向量叉乘的属性:
判断三个向量是否共面:![]()
三:应用1 - 求两直线的交点:
(1)2D直线方程: ![]()
(2)将直线1带入直线2中: ![]() ,叉乘等于0,意味着两向量共线。
,叉乘等于0,意味着两向量共线。
(3)求交点:

四:应用2 - 求三个平面的交点:
(1):三个平面方程:

(2):三个平面方程,三个未知数,利用克拉默法则求解即可。
三:实现
#ifndef _POINT_H_
#define _POINT_H_#include <iostream>
#include <cmath>class Point2D
{
public:float x, y;Point2D() {}Point2D(float x, float y) : x(x), y(y) {}Point2D &operator+=(const Point2D &t){x += t.x;y += t.y;return *this;}Point2D &operator-=(const Point2D &t){x -= t.x;y -= t.y;return *this;}Point2D &operator*=(float t){x *= t;y *= t;return *this;}Point2D &operator/=(float t){x /= t;y /= t;return *this;}Point2D operator+(const Point2D &t) const{return Point2D(*this) += t;}Point2D operator-(const Point2D &t) const{return Point2D(*this) -= t;}Point2D operator*(float t) const{return Point2D(*this) *= t;}Point2D operator/(float t) const{return Point2D(*this) /= t;}float dot(const Point2D& b) const{return x * b.x + y * b.y;}friend std::ostream &operator<<(std::ostream &out, const Point2D &t){out << '(' << t.x << ',' << t.y << ')';return out;}};Point2D operator*(float a, const Point2D &b)
{return b * a;
}float dot(const Point2D& a, const Point2D& b)
{return a.dot(b);
}float norm(const Point2D& a)
{return dot(a, a);
}double abs(const Point2D& a) {return sqrt(norm(a));
}double proj(const Point2D& a, const Point2D& b)
{return dot(a, b) / abs(b);
}double angle(const Point2D& a, const Point2D& b)
{return acos(dot(a, b) / abs(a) / abs(b));
}float cross(const Point2D& a, const Point2D& b)
{return a.x * b.y - a.y * b.x;
}Point2D intersect(const Point2D& a1, const Point2D& d1, const Point2D& a2, const Point2D& d2)
{return a1 + cross(a2 - a1, d2) / cross(d1, d2) * d1;
}class Point3D: public Point2D
{
public:float z;Point3D() {}Point3D(float x, float y, float z) : Point2D(x, y), z(z) {}Point3D &operator+=(const Point3D &t){x += t.x;y += t.y;z += t.z;return *this;}Point3D &operator-=(const Point3D &t){x -= t.x;y -= t.y;z -= t.z;return *this;}Point3D &operator*=(float t){x *= t;y *= t;z *= t;return *this;}Point3D &operator/=(float t){x /= t;y /= t;z /= t;return *this;}Point3D operator+(const Point3D &t) const{return Point3D(*this) += t;}Point3D operator-(const Point3D &t) const{return Point3D(*this) -= t;}Point3D operator*(float t) const{return Point3D(*this) *= t;}Point3D operator/(float t) const{return Point3D(*this) /= t;}float dot(const Point3D &t) const{return x * t.x + y * t.y + z * t.z;}friend std::ostream &operator<<(std::ostream &out, const Point3D &t){out << '(' << t.x << ',' << t.y << ',' << t.z << ')';return out;}
};Point3D operator*(float a, Point3D b)
{return b * a;
}float dot(const Point3D& a, const Point3D& b)
{return a.dot(b);
}float norm(const Point3D& a)
{return dot(a, a);
}double abs(const Point3D& a) {return sqrt(norm(a));
}double proj(const Point3D& a, const Point3D& b)
{return dot(a, b) / abs(b);
}double angle(const Point3D& a, const Point3D& b)
{return acos(dot(a, b) / abs(a) / abs(b));
}Point3D cross(const Point3D& a, const Point3D& b)
{return Point3D(a.y * b.z - a.z * b.y,a.z * b.x - a.x * b.z,a.x * b.y - a.y * b.x);
}float triple(const Point3D& a, const Point3D& b, const Point3D& c)
{return dot(a, cross(b, c));
}Point3D intersect(const Point3D& a1, const Point3D& n1, const Point3D& a2, const Point3D& n2, const Point3D& a3, const Point3D& n3)
{Point3D x(n1.x, n2.x, n3.x);Point3D y(n1.y, n2.y, n3.y);Point3D z(n1.z, n2.z, n3.z);Point3D d(dot(a1, n1), dot(a2, n2), dot(a3, n3));return Point3D(triple(d, y, z),triple(x, d, z),triple(x, y, d)) / triple(n1, n2, n3);
}#endif
相关文章:

C++ 几何算法 - 向量点乘,叉乘及其应用
一:点乘介绍 1. 向量点乘: 2. 向量点乘的性质: 3. 向量点乘公式: 4. 向量的点乘的属性: (1):向量与自身做点乘,会得到向量长度的平方: (2…...
Taro学习记录(具体项目实践)
一、安装taro-cli 二、项目文件 三、项目搭建 1、Eslint配置 在项目生成的 .eslintrc 中进行配置 {"extends": ["taro/react"], //一个配置文件,可以被基础配置中的已启用的规则继承"parser": "babel/eslint-parser…...
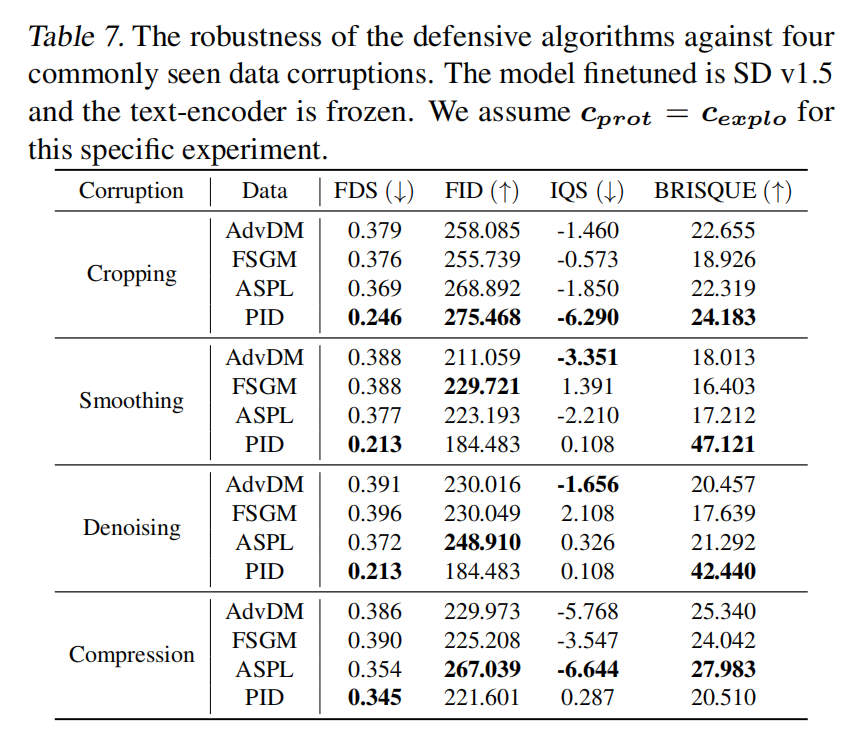
ICML 2024 | 矛与盾的较量!北大提出提示无关数据防御保护算法PID
文章链接:https://arxiv.org/pdf/2406.15305 代码地址:https://github.com/PKU-ML/Diffusion-PID-Protection 亮点直击 本文在实证观察中发现,保护阶段和利用阶段之间的提示不匹配可能会削弱当前数据保护算法的有效性。本文深入探讨了利用LDM…...

Oracle聚合函数LISTAGG和WM_CONCAT简介
目录 Oracle聚合函数LISTAGG和WM_CONCAT简介LISTAGG 函数1.语法2.示例3.去除重复值 WM_CONCAT 函数1.语法2.示例3.去除重复值 比较1.性能2.排序与分隔符3.去除重复值 Oracle聚合函数LISTAGG和WM_CONCAT简介 在处理数据库中的数据聚合任务时,我们经常需要将多行数据…...

【Unity】多种寻路算法实现 —— BFS,DFS,Dijkstra,A*
本实验寻路算法均基于网格实现,整体称呼为Grid,单个瓦片称之为Tile 考虑程序处理的简洁性,所有算法使用同一种Tile,且权值点,A*所需的记录数值也全部放在Tile中记录 前排贴上代码仓库链接: GitHub - Sir…...

十大游戏设计软件:创意实现的利器
在数字娱乐的多彩世界里,游戏设计无疑是一项充满创意与技术挑战的艺术。随着技术的进步,游戏设计师的手中拥有了一系列强大的工具,它们让想象中的世界得以呈现,让玩家的体验更加丰富和真实。本文将带你走进游戏设计的幕后…...

Pandas高级操作:多级索引、窗口函数、数据透视表等
在数据处理和分析中,pandas库提供了强大的功能,支持从简单到复杂的数据操作。本文将介绍一些pandas的高级操作,包括多级索引(MultiIndex)、窗口函数(Window Functions)、数据透视表与复杂聚合、数据合并与连接、高级数据变换以及时间序列数据的高级处理。 1. 多级索引(…...

mysql源码编译启动debug
对于没有C语言基础的同学来说,想看看源码,在搞定编辑器做debug的时候就被劝退了,发生点啥了,完全看不懂,不知道从哪里入手去做debug;我为了看看 mysql 的 insert buffer 到底存的是索引页还是数据页&#x…...

吴恩达机器学习-C1W3L2-逻辑回归之S型函数
可选实验:逻辑回归 在这个不评分的实验中,你会 探索sigmoid函数(也称为logistic函数)探索逻辑回归;哪个用到了s型函数 import numpy as np %matplotlib widget import matplotlib.pyplot as plt from plt_one_addpt_onclick import plt_one_addpt_onclick from l…...

P-one新增火焰图-为性能测试开启新视野
随着软件业务流程的日益复杂,传统的性能测试方法已经难以满足对性能问题精准定位的需求。测试人员需要一种更加直观、全面的方式来分析软件在运行过程中的性能表现,以便快速准确地找到性能瓶颈并进行优化。因此,我们在性能测试平台P-One中加入…...

CTF-web基础 TCP/UDP协议
传输层协议由TCP/UDP协议组成,来控制信息的传输,二者有什么区别呢,TCP比较靠谱,但是UDP速度比较快一点。 TCP协议 Transmission Control protocol, 三次握手:先给服务器传输询问要发消息,然后…...

sql常用语法总结
SQL(Structured Query Language,结构化查询语言)是一种用于管理和操作关系数据库的标准编程语言。本文用来记录一些接触到的sql语句,随着学习不断进行更新: 选择数据 - SELECT 语句用于从数据库表中检索数据。 SELECT column1, column2 FROM table_name;插入数据 - INSERT…...
,判断该整数的绝对值是否为回文数。)
实验八 题目描述 从键盘上输入任意一个整数(正负数皆可),判断该整数的绝对值是否为回文数。
实验八 题目描述 从键盘上输入任意一个整数(正负数皆可),判断该整数的绝对值是否为回文数。[提示:取数的绝对值,然后使用用循环语句从该绝对值的末位开始至最高位,重新构造一个数,…...

IsaacLab | Workflow 中 rsl_rl 的 play.py 脚本精读
如是我闻: 在用IsaacLab 做强化学习实验时,回顾已训练好的模型需要调用workflow中的play.py脚本,以下是对rsl_rl的play.py脚本的逐行精读。 1. 版权声明和文件描述 # Copyright (c) 2022-2024, The Isaac Lab Project Developers. # All ri…...
我错了该怎么整?)
PYTHON专题-(8)我错了该怎么整?
什么是异常处理? 异常处理是一种机制,用于在程序执行期间发生错误或异常时,对发生的异常进行捕获、处理和恢复,以确保程序能够继续执行或正确地终止。异常处理可以包括捕获异常、处理异常,以及执行相应的操作来处理异常…...

【自然资源】设施农业用地的学习梳理
【自然资源】设施农业用地的学习梳理 什么是设施农业用地? 2019年12月17日,自然资源部 、农业农村部印发的《关于设施农业用地管理有关问题的通知》规定:设施农业用地包括农业生产中直接用于作物种植和畜禽水产养殖的设施用地。其中&#x…...
【秋招笔试】24-07-27-OPPO-秋招笔试题(后端卷)
🍭 大家好这里是清隆学长 ,一枚热爱算法的程序员 💻 ACM金牌团队🏅️ | 多次AK大厂笔试 | 编程一对一辅导 ✨ 本系列打算持续跟新 秋招笔试题 👏 感谢大家的订阅➕ 和 喜欢💗 ✨ 笔试合集传送们 -> 🧷春秋招笔试合集 💡 01.二进制反转游戏 问题描述 K小姐…...

JS 补充内容
一、dir 打印对象 二、获取 html 中的元素 常用的两种方式 其他获取元素的方法 三、 innerText 四、innerHTML 五、修改元素的值 六、鼠标放上去,显示图片的提示文字 img . title 七、获取 N ~ M 之间的随机整数 八、修改属性样式 1. style 2. className 将后面 …...

H5+JS 4096小游戏
主要实现 1.使用WASD或方向按钮控制游戏 2.最高值4096,玩到4096视为胜利 3.随机生成2、4、8方块 4.移动方块 5.合并方块 JS代码干了什么 初始化游戏界面:创建游戏板和控制按钮。 定义游戏相关变量:如棋盘大小、棋盘状态、得分等。 初始化棋…...

常见中间件漏洞(二、WebLogin合集)
目录 二、WebLogic Weblogic介绍 2.1 后台弱口令GetShell 漏洞描述 影响范围 环境搭建 漏洞复现 2.2 CVE-2017-3506 漏洞描述 影响版本 环境搭建 漏洞复现 2.3 CVE-2019-2725 漏洞描述 影响版本 环境搭建 漏洞复现 2.4 CVE-2018-2628 漏洞描述 漏洞影响 环…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...
