评价公式-均方误差
均方误差的公式可以通过以下步骤推导得出:
假设有n个样本,真实值分别为y₁, y₂, ……, yₙ,预测值分别为ŷ₁, ŷ₂, ……, ŷₙ。
首先,我们可以定义误差(error)为预测值与真实值之间的差:
eᵢ = yᵢ - ŷᵢ
则第i个样本的误差平方为:
eᵢ² = (yᵢ - ŷᵢ)²
我们希望得到所有样本误差平方的平均数,即均方误差。因此,我们可以计算所有样本误差平方的和,再除以样本数n:
MSE = (1/n) * Σ(yᵢ - ŷᵢ)² (i=1,2,…,n)
将误差平方代入上式,可以得到:
MSE = (1/n) * Σ(yᵢ - ŷᵢ)²
= (1/n) * (e₁² + e₂² + … + eₙ²)
= (1/n) * ((y₁ - ŷ₁)² + (y₂ - ŷ₂)² + … + (yₙ - ŷₙ)²)
继续化简,可以得到:
MSE = (1/n) * ((y₁² - 2y₁ŷ₁ + ŷ₁²) + (y₂² - 2y₂ŷ₂ + ŷ₂²) + … + (yₙ² - 2yₙŷₙ + ŷₙ²))
= (1/n) * (y₁² + y₂² + … + yₙ² - 2y₁ŷ₁ - 2y₂ŷ₂ - … - 2yₙŷₙ + ŷ₁² + ŷ₂² + … + ŷₙ²)
由于真实值的平方和常数,预测值的平方和常数,因此,我们可以将式子进一步简化:
MSE = (1/n) * (y₁² + y₂² + … + yₙ² - 2y₁ŷ₁ - 2y₂ŷ₂ - … - 2yₙŷₙ + ŷ₁² + ŷ₂² + … + ŷₙ²)
= (1/n) * (Σy² - 2Σ(yᵢŷᵢ) + Σŷ²)
= (1/n) * (Σy² - 2Σyᵢŷᵢ + Σŷ²)
因此,均方误差可以用样本真实值的平方和、样本真实值与预测值的乘积之和、样本预测值的平方和来计算。
相关文章:

评价公式-均方误差
均方误差的公式可以通过以下步骤推导得出: 假设有n个样本,真实值分别为y₁, y₂, ……, yₙ,预测值分别为ŷ₁, ŷ₂, ……, ŷₙ。 首先,我们可以定义误差(error)为预测值与真实值之间的差: …...

冲击蓝桥杯-时间问题(必考)
目录 前言: 一、时间问题 二、使用步骤 1、考察小时,分以及秒的使用、 2、判断日期是否合法 3、遍历日期 4、推算星期几 总结 前言: 时间问题可以说是蓝桥杯,最喜欢考的问题了,因为时间问题不涉及到算法和一些复杂的知识…...

10个杀手级应用的Python自动化脚本
10个杀手级应用的Python自动化脚本 重复的任务总是耗费时间和枯燥的。想象一下,逐一裁剪100张照片,或者做诸如Fetching APIs、纠正拼写和语法等任务,所有这些都需要大量的时间。为什么不把它们自动化呢?在今天的文章中,…...

2023史上最全软件测试工程师常见的面试题总结 备战金三银四
在这里我给大家推荐一套专门讲解软件测试简历,和面试题的视频,实测有效,建议大家可以看看! 春招必看已上岸,软件测试常问面试题【全网最详细,让你不再踩坑】_哔哩哔哩_bilibili春招必看已上岸,…...

2023年全国最新安全员精选真题及答案29
百分百题库提供安全员考试试题、建筑安全员考试预测题、建筑安全员ABC考试真题、安全员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 81.(单选题)同一建筑施工企业在12个月内连续发生(&…...

关系数据库的7个基本特征
文章目录关系数据库中的二维表─般满足7个基本特征:①元组(行)个数是有限的——元组个数有限性。 ②元组(行)均不相同——元组的唯—性。 ③元组(行)的次序可以任意交换——元组的次序无关性。 ④元组(行)的分量是不可分割的基本特征——元组分量的原子性。 ⑤属性(列)名各不相…...

2023QT面试题总会
1、Qt信号槽机制的优势 (1)类型安全。需要关联的信号和槽的签名必须是等同的,即信号的参数类型和参数个数同接收该信号的槽的参数类型和参数个数相同。不过,一个槽的参数个数是可以少于信号的参数个数的,但缺少的参数…...

【微信小程序】-- npm包总结 --- 基础篇完结(四十七)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &…...
Leetcode刷题之经典双指针问题
光是话不行,要紧的是做。 ——鲁迅 目录 一.什么是双指针问题? 二.最接近的三数之和 第一种暴力法: 第二种双指针: 三.移除元素 第一种暴力法: 第二种双指针: 四.盛最…...
C语言学习之路--指针篇
目录一、前言二、指针一、指针是什么1、指针的重要理解2、指针变量3、其他问题二、指针和指针类型1、指针—整数2、指针的解引用三、野指针1、野指针成因2、如何规避野指针四、指针的运算1、指针—指针2、指针的关系运算五、指针和数组六、二级指针七、指针数组一、前言 本人是…...
吃透Java面试题,建议收藏
本文已经收录到Github仓库,该仓库包含计算机基础、Java基础、多线程、JVM、数据库、Redis、Spring、Mybatis、SpringMVC、SpringBoot、分布式、微服务、设计模式、架构、校招社招分享等核心知识点,欢迎star~ Github地址:https://github.com/…...

华为OD机试题,用 Java 解【最差产品奖】问题 | 含解题说明
华为Od必看系列 华为OD机试 全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典本篇题目:最差产品奖 题目 A 公司准备对…...
Redis缓存优化
数据库在用户数量多,系统访问量大的时候,系统性能会下降,用户体验差。1.缓存优化作用:1.降低数据库的访问压力2.提高系统的访问性能3.从而提高用户体验实现思路:1.先查询缓存2.如果缓存有数据,直接返回3.如…...
:楼梯问题)
少儿Python每日一题(23):楼梯问题
原题解答 本次的题目如下所示: 楼梯有n阶台阶,上楼可以一步上1阶,也可以一步上2阶,走完n阶台阶共有多少种不同的走法? 输入格式: 输入楼梯的阶梯数n 输出格式: 输出不同走法的个数 输入样例: 10 输出样例: 89 这是一道非常经典的题目,我们可以先寻找一下上楼梯的规律…...

【Leetcode】队列实现栈和栈实现队列
目录 一.【Leetcode225】队列实现栈 1.链接 2.题目再现 3.解法 二.【Leetcode232】栈实现队列 1.链接 2.题目再现 3.解法 一.【Leetcode225】队列实现栈 1.链接 队列实现栈 2.题目再现 3.解法 这道题给了我们两个队列,要求去实现栈; 首先&…...

(一)Tomcat源码阅读:查看官网,厘清大概轮廓
一、进入官网 点击以下链接进入官网:Apache Tomcat - Welcome!,点击介绍进入介绍,查看tomcat的项目结构。 二、查看项目结构 进入介绍后,我们可以看到下面的这些东西,这些对于tomcat是比较重要的,我们要一一对其进行解读。 这段…...
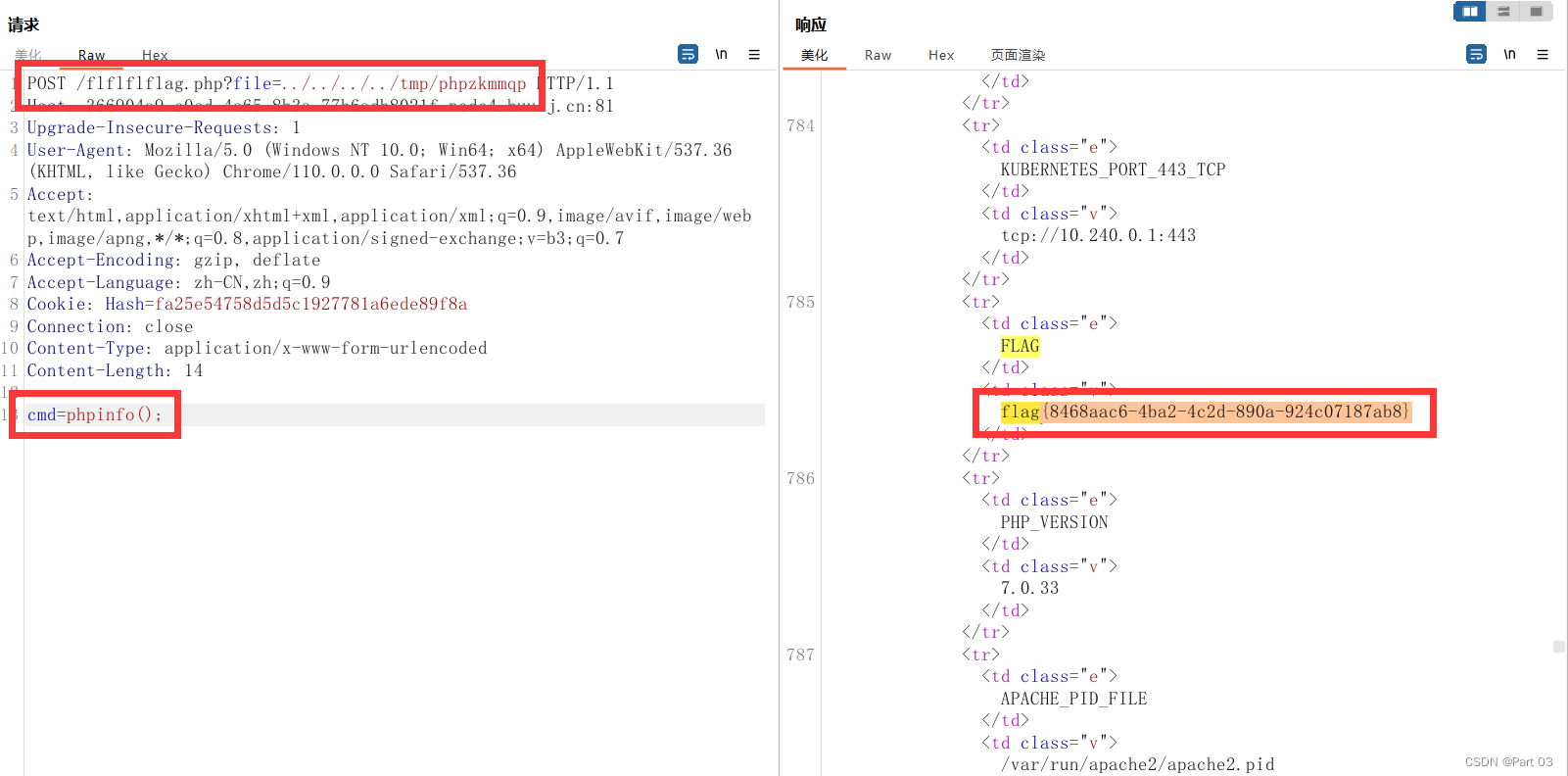
刷题记录(2023.3.14 - 2023.3.18)
[第五空间 2021]EasyCleanup 临时文件包含考点 分析源码,两个特殊的点,一个是 eval,另一个是 include eval 经过了 strlen filter checkNums 三个函数 include 经过了 strlen filter 两个函数 filter 检测是否包含特定的关键字或字符 fun…...

http协议 - 笔记
1 http协议 -- post,get,delete 如何使用http协议post - /api/v1/User/1 要使用 HTTP 协议 POST 方法向 /api/v1/User/1 发送请求,您可以使用一个 HTTP 客户端(例如 Postman、cURL 或浏览器扩展程序)并按照以下步骤操作: 打开您的 HTTP 客户端。在 URL 地址栏中输入 /a…...
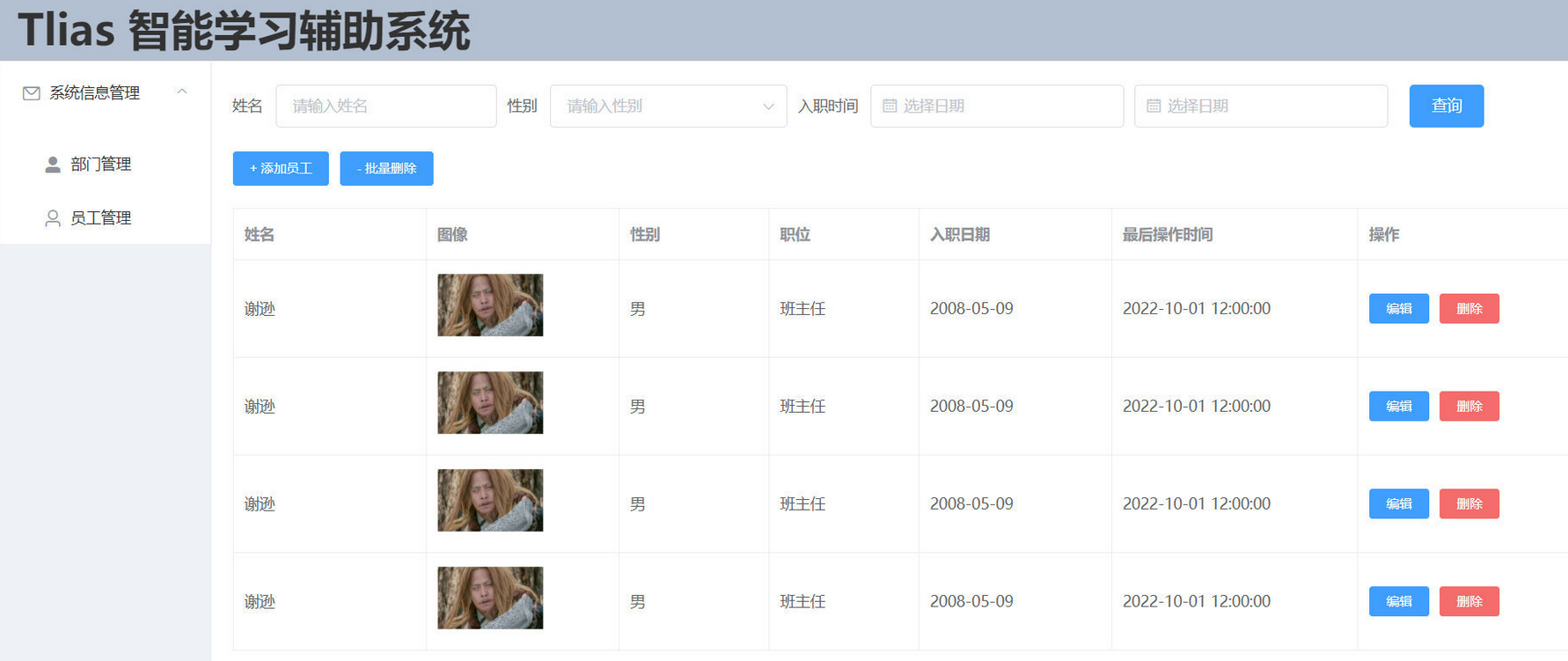
第十八天 Vue-前端工程化总结
目录 Vue-前端工程化 1. 前后端分离开发 1.1 介绍 1.2 Yapi 2. 前端工程化 2.1 环境准备 2.2 Vue项目简介 2.3 Vue项目开发流程 3. Vue组件库Element 3.1 快速入门 3.2 常用组件 3.3 案例 Vue-前端工程化 前面我们已经讲解了HTML、CSS、JavaScript以及Vue等知识。已…...
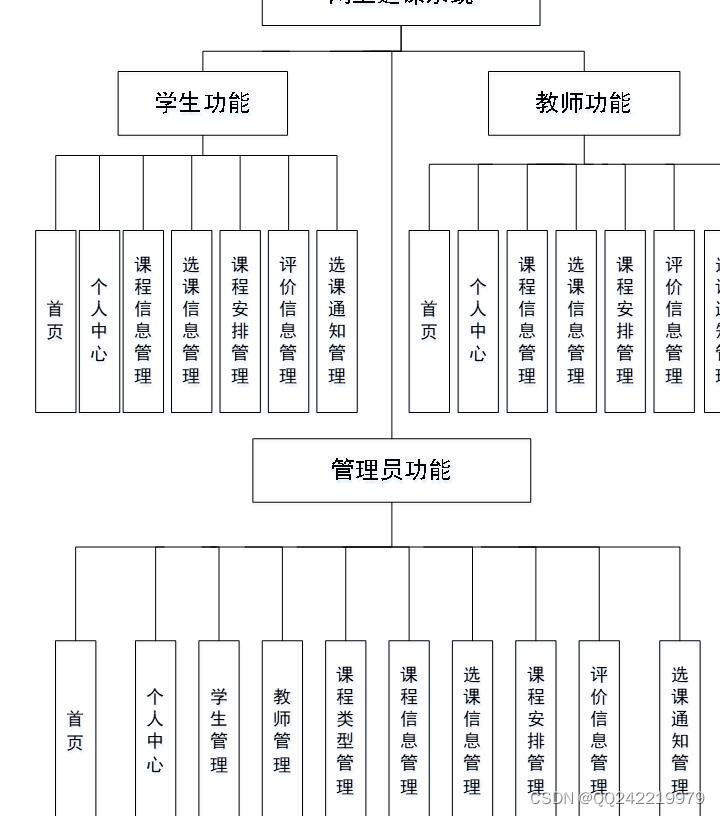
python网上选课系统django-PyCharm
学生选课信息管理系统,可以有效的对学生选课信息、学生个人信息、教师个人信息等等进行管理。 开发语言:Python 框架:django Python版本:python3.7.7 数据库:mysql 数据库工具:Navicat11 开发软件&#x…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...
