图论(强联通分量)
在图论中,特别是在讨论有向图(Directed Graph)时,我们常常需要了解图的结构特性,比如强联通分量(Strongly Connected Components, SCC)。了解强联通分量中的各种边对于理解图的整体结构以及某些算法(如Tarjan's算法或Kosaraju's算法)是非常重要的。以下是对强联通分量及其边类型的解释:
强联通分量(SCC)
强联通分量是一个子图,其中每对顶点之间都有路径相互可达。换句话说,一个强联通分量内的任意两个顶点 u 和 v 都满足 u 到 v 和 v 到 u 之间存在路径。
边的分类

板子如下
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
vector<int> e[N]; // 存储图的邻接表
int dfn[N], low[N]; // 存储每个节点的时间戳和最小到达时间
bool ins[N]; // 标记节点是否在栈中
int idx, bel[N], cnt; // 时间戳、节点所属的强联通分量编号、强联通分量计数
stack<int> stk; // 用于 Tarjan 算法的栈
vector<vector<int>> scc;// 存储所有的强联通分量
int n, m; // 节点数和边数void dfs(int u) {dfn[u] = low[u] = ++idx; // 初始化时间戳ins[u] = true; // 标记节点在栈中stk.push(u); // 将节点压入栈中for (auto v : e[u]) { // 遍历节点 u 的所有邻接点 vif (!dfn[v]) { // 如果节点 v 尚未访问dfs(v); // 递归访问节点 vlow[u] = min(low[u], low[v]); // 更新节点 u 的最小到达时间} else if (ins[v]) { // 如果节点 v 在栈中low[u] = min(low[u], dfn[v]); // 更新节点 u 的最小到达时间}}if (dfn[u] == low[u]) { // 如果节点 u 是强联通分量的根节点vector<int> c; // 创建一个新的强联通分量++cnt;while (1) {int v = stk.top(); // 弹出栈顶节点c.push_back(v); // 将节点添加到当前强联通分量中ins[v] = false; // 标记节点不在栈中bel[v] = cnt; // 标记节点所属的强联通分量编号stk.pop(); // 弹出栈顶节点if (u == v) break; // 如果节点 u 是栈顶节点,结束循环}sort(c.begin(), c.end()); // 对强联通分量内的节点排序scc.push_back(c); // 将强联通分量添加到结果中}
}int main() {ios::sync_with_stdio(0);cin.tie(0);cin >> n >> m;for (int i = 1; i <= m; i++) {int u, v;cin >> u >> v;e[u].push_back(v); // 构建邻接表}for (int i = 1; i <= n; i++) {if (!dfn[i]) dfs(i); // 对每个未访问的节点进行 DFS}sort(scc.begin(), scc.end()); // 对所有的强联通分量排序cout << cnt << endl; // 输出强联通分量的数量for (auto c : scc) { // 输出每个强联通分量for (auto u : c) {cout << u << " ";}cout << endl;}return 0;
}
题目链接 洛谷 B3609
参考文献 scc
相关文章:

图论(强联通分量)
在图论中,特别是在讨论有向图(Directed Graph)时,我们常常需要了解图的结构特性,比如强联通分量(Strongly Connected Components, SCC)。了解强联通分量中的各种边对于理解图的整体结构以及某些…...

LLaMA- Adapter V2: Parameter-Efficient Visual Instruction Model
发表时间:28 Apr 2023 论文链接:https://arxiv.org/pdf/2304.15010 作者单位: Shanghai Artificial Intelligence Laboratory Motivation:如何有效地将大型语言模型 (LLM) 转换为指令追随者最近是一个流行的研究方向࿰…...

【爬虫实战】利用代理爬取Temu电商数据
引言 在行业竞争激烈、市场变化快速的跨境电商领域,数据采集可以帮助企业深入了解客户需求和行为,分析市场趋势和竞争情况,从而优化产品和服务,提高客户满意度和忠诚度。同时,数据采集可以实时跟踪库存水平和销售情况&…...

【MATLAB源码-第244期】基于MATLAB的BP神经网络语音特征信号分类,输出原信号与预测信号对比图以及预测误差和正确率。
操作环境: MATLAB 2022a 1、算法描述 BP神经网络(Back Propagation Neural Network)是一种广泛应用于模式识别和分类问题的人工神经网络。在本次语音特征信号分类任务中,我们将详细描述如何通过BP神经网络实现对四类语音信号的…...

HarmonyOS 习题(二)
1、在类Web开发范式自定义组件创建后,加入到Page组件树时,会触发以下哪一项回调。 A)Onlnit B)OnAttached C)OnLayoutReady D)OnDetached 答案:B 分析: onlnit:自定义组件初始化生命周期回调&a…...

如何搭建一个圈子社区系统?开源社交陪玩交友圈子论坛帖子系统保姆级搭建教程!
整体部署流程如下: 1.获取源码/前后端分离,前端Uniapp vue2.0 后端thinkphp6(Gitee直达) 2.服务器安装宝塔(已有宝塔请安装环境,Nginx或者Apache/ php 7.3/ mysql 5.6 ) 3.进入宝塔添加网站&…...
Delphi5实现身份证检验(DLL版)
效果图 身份证行政区划分代码 识别归属地需要行政区划分,都在data.txt文档里面了。 最后一位校验码 根据上面的原理编写程序即可。 {这个函数计算最后一位检验码是否正确,ID是18位身份证号字符串,结果返回字符串} function IDcheck(ID:stri…...

linux下的C++程序
1.安装g编译环境(c)、gcc编译环境(c语言) sudo yum install gcc或者gcc-c //安装gcc/g编译(用管理员权限弄) 验证是否安装成功 gcc或者g --version //如果显示版本号,则表示安装成功 sudo yum remove g…...

selfAttention 中的dk到底是什么
在Self-Attention机制中,为什么需要对 Q K T QK^T QKT 的结果进行缩放,除以 d k \sqrt{d_k} dk 。以下是详细解释: 缩放的原因 除以 d k \sqrt{d_k} dk 的原因有两个: 防止输入过大:如果不缩放…...

安装MongoDB UI客户端工具:mongodb-compass-1.40.2-win32-x64.msi
文章目录 1、安装 mongodb-compass-1.40.2-win32-x64.msi2、安装后配置链接地址: 1、安装 mongodb-compass-1.40.2-win32-x64.msi 2、安装后配置链接地址:...
一行命令搞定内网穿透
一行命令搞定内网穿透 一款开源免费的内网穿透工具:localtunnel ,基于 nodejs 实现,无需修改 DNS 和防火墙设置,方便快捷的将内网服务暴露到外网,为开发人员、测试人员以及需要分享本地项目的人提供实时的公网访问方式…...

C语言——扫雷游戏
扫雷游戏通常是一个由方格组成的区域内进行的,其中随机分布着一定数量的地雷 。玩家的目标是通过点击方格来标记出所有地雷的位置,同时避免自己点到地雷而导致游戏失败。游戏开始时,玩家通常只能看到一部分方格,而其余的方格则需要…...

【LLM】-16-评估LLM-与标准答案的差距
目录 1、评估回答是否正确 1.1、util_zh 1.2、eval_zh 1.3、评估 2、评估生成答案与标准答案的差距 2.1、eval_zh2 2.2、评估 即使没有提供的理想答案,只要能制定一个评估标准,就可以使用一个 LLM 来评估另一个 LLM 的输出。 如果可以提供理想答…...

WeNet 2.0:更高效的端到端语音识别工具包
WeNet 2.0:更高效的端到端语音识别工具包 原文链接:[2203.15455] WeNet 2.0: More Productive End-to-End Speech Recognition Toolkit (arxiv.org) 1.摘要 WeNet是一个开源的端到端语音识别工具包,WeNet 2.0在此基础上进行了四项主要更新,…...

阿里大模型调用 = 》通义千问大语言模型
背景:简单的通过API或者SDK在线调用阿里云大模型(基于百炼平台),基于在线知识库 参考地址:安装阿里云百炼SDK_大模型服务平台百炼(Model Studio)-阿里云帮助中心 (aliyun.com) 1、获取API-KEY 当您通过API/SDK调用大模…...

idea使用free流程,2024idea免费使用
1.先到官网下载,这里选择win系统的,点击下图的.exe https://www.jetbrains.com/idea/download/?sectionwindows 2.下载好后基本上就是一直点击“下一步”到直到安装好,安装好后先打开软件后关闭退出 3.下载配配套资料 链接: https://pan.ba…...

算法_链表专题---持续更新
文章目录 前言两数相加题目要求题目解析代码如下 两两交换链表中的结点题目要求题目解析代码如下 重排链表题目要求题目解析代码如下 合并K个升序链表题目要求题目解析 K个一组翻转链表题目要求题目解析代码如下 前言 本文将记录leetcode链表算法题解,包含题目有&a…...

在Windows MFC\C++编程中,如何使用OnCopyData函数
在C中,OnCopyData 函数通常不是标准C库的一部分,而是与特定的图形用户界面(GUI)框架相关联,如Microsoft Foundation Classes (MFC) 或 Windows API 编程。在MFC应用程序中,OnCopyData 是用于处理来自其他应…...

【Qt】项目代码
main.cpp文件 argc:命令行参数个数。*argv[ ]:每一个命令行参数的内容。main的形参就是命令行参数。QApplication a(argc, argv) 编写一个Qt的图形化界面程序,一定需要QApplication对象。 widget w; 在创建项目的时候,勾选widg…...
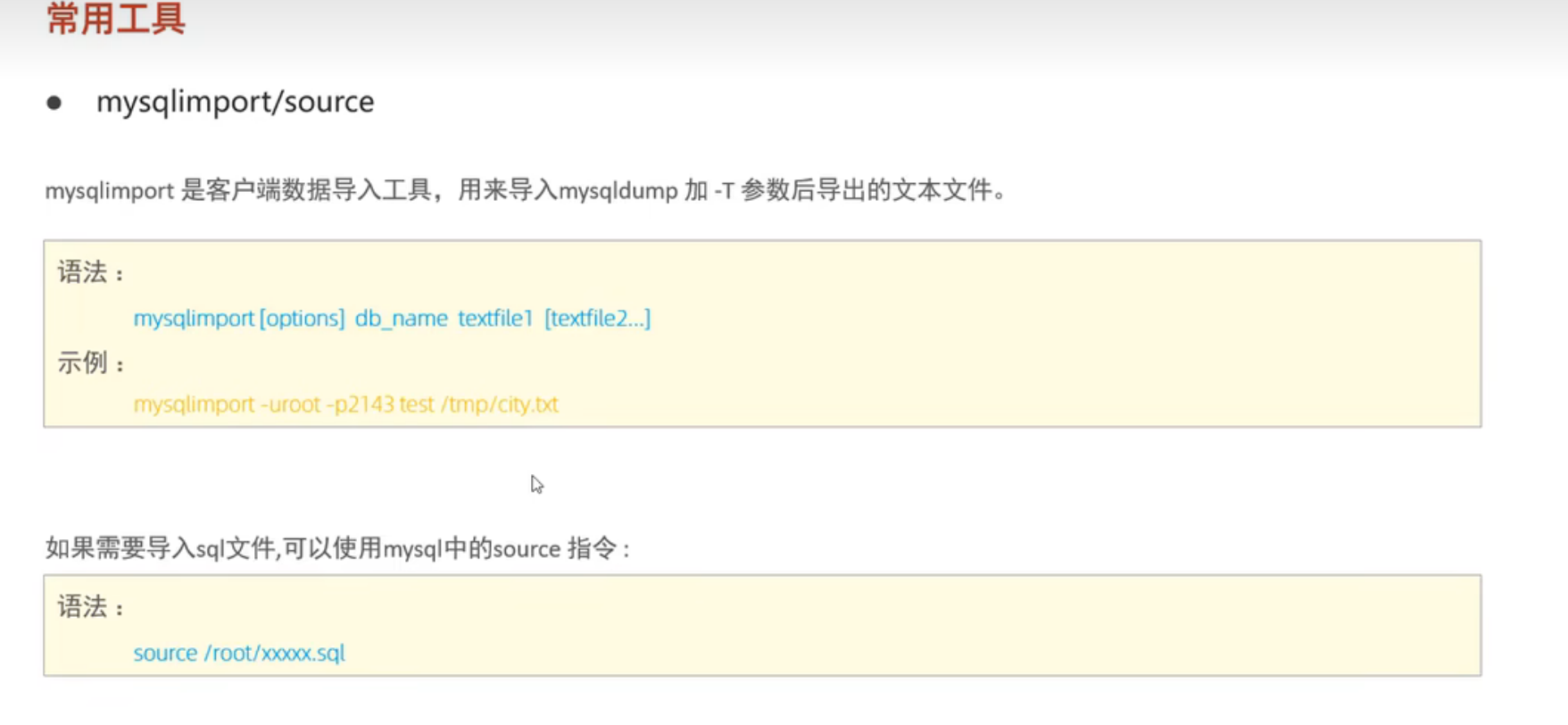
MySQL中常用工具
MySQL自带的系统数据库 常用工具 MySQL mysqladmin mysqlbinlog mysqldump mysqlimport/source mysqlimport只能导入文本文件,不能导入sql文件...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...
