当前位置： 首页 > news >正文

jupyter for c++

news 2026/2/10 7:50:30

jupyter for c++

jupyter for c++

  • jupyter for c++
    • 配置环境
    • 问题
  • 参考文档

配置环境

  • 需要 clang 编译器

  • 安装 aconda

    • 默认情况下，anaconda navigator包与anaconda Distribution一起安装，并包含依赖包qt。默认情况下，qt的所有依赖项也应安装，但某些版本的Anaconda Distribution可能需要安装以下扩展依赖项，以便在Linux中使用GUI（图形用户界面）包：
    apt-get install libgl1-mesa-glx libegl1-mesa libxrandr2 libxrandr2 libxss1 libxcursor1 libxcomposite1 libasound2 libxi6 libxtst6
    • 下载安装器
    # Replace <INSTALLER_VERSION> with the version of the installer file you want to download
# For example, https://repo.anaconda.com/archive/Anaconda3-2023.09-0-Linux-x86_64.sh

相关文章：

jupyter for c++

jupyter for c++ jupyter for c++ jupyter for c++配置环境问题参考文档配置环境 需要 clang 编译器 安装 aconda 默认情况下，anaconda navigator包与anaconda Distribution一起安装，并包含依赖包qt。默认情况下，qt的所有依赖项也应安装，但某些版本的Anaconda Distribution…...

编程日记 2024/8/7 22:07:39

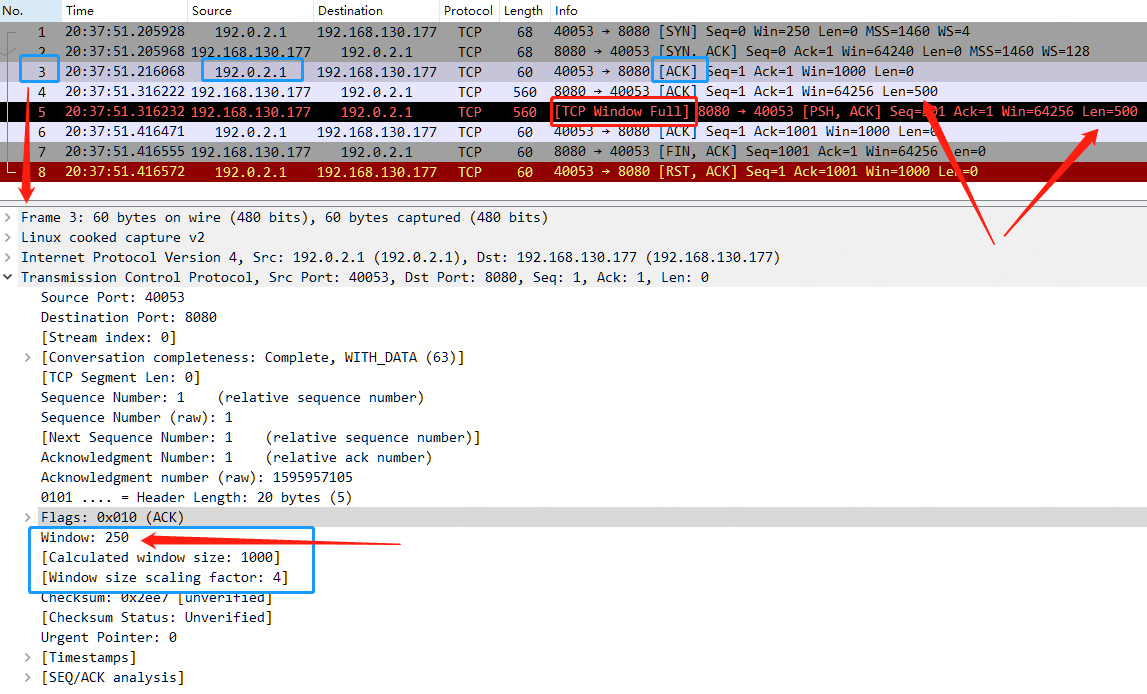
TCP Analysis Flags 之 TCP Window Full

前言 默认情况下&#xff0c;Wireshark 的 TCP 解析器会跟踪每个 TCP 会话的状态&#xff0c;并在检测到问题或潜在问题时提供额外的信息。在第一次打开捕获文件时&#xff0c;会对每个 TCP 数据包进行一次分析&#xff0c;数据包按照它们在数据包列表中出现的顺序进行处理。可…...

编程日记 2024/8/7 22:04:36

相关性检验

文章目录 Pearson相关系数Spearman等级相关系数Cochrans Q检验Kappa一致性系数Kendall相关系数实例分析总结 在数据分析的广阔天地中&#xff0c;相关性检验是探索变量间关系的一把钥匙。本文将带领大家了解几种常用的相关性检验方法&#xff1a;Pearson、Spearman、Cochran’s…...

编程日记 2024/8/7 22:03:34

【python】Django运行报错分析：ImproperlyConfigured 错误解决办法

✨✨ 欢迎大家来到景天科技苑✨✨ &#x1f388;&#x1f388; 养成好习惯&#xff0c;先赞后看哦~&#x1f388;&#x1f388; &#x1f3c6; 作者简介&#xff1a;景天科技苑 &#x1f3c6;《头衔》&#xff1a;大厂架构师&#xff0c;华为云开发者社区专家博主&#xff0c;…...

编程日记 2024/8/7 22:02:33

AS01/AS11 创建固资和子资产

AS01&#xff1a;创建资产卡片 定义该资产的折旧费用&#xff0c;应该归结到哪个成本中心。 如果一台设备停止使用&#xff0c;可以勾选。停止折旧。 该界面维护折旧码和折旧的时间。 维护完之后点击保存。 系统生成一个资产卡片号。 AS02-修改资产卡片号 更改不同时间段&…...

编程日记 2024/8/7 22:01:32

vue3数字动画插件countup.js

countup.js 是一个轻量级的 JavaScript 库&#xff0c;允许你为网站上显示统计数据或计数器时平滑地动画化数字。CountUp 类被用来创建计数器实例&#xff0c;可以平滑地从一个数值变化到另一个数值。 只是用户视觉更好一些。 1、安装插件 npm i countup.js2、个人是封装了组件…...

编程日记 2024/8/7 21:57:29

aspeed2600 GPIO分析与适配ipmitool power status, ipmitool power on/off

1.说明 本节以x86-power-control/src/power_control.cpp为基础&#xff0c;分析整个GPIO的调用流程&#xff0c;实现简单的ipmitool power on/off,ipmitool power status的管理。 1.资源:x86-power-control:https://github.com/openbmc/x86-power-control2.相关文件: meta-ph…...

编程日记 2024/8/7 21:56:28

在C#中配置ini文件以及封装ini类

在C#中使用 DllImport 属性从 kernel32.dll 导入函数来写入和读取Windows的INI文件&#xff0c;你可以使用 WritePrivateProfileString 来写入数据&#xff0c;使用 GetPrivateProfileString 来读取数据。 以下是如何使用这些函数的示例&#xff1a; 写入INI文件 using Syst…...

编程日记 2024/8/7 21:55:27

使用git上传代码到github

1、设置用户名及邮箱 git config user.name"你的用户名"git config user.email"xxxxx.com" 2、查看配置 git config -l 3、生成秘钥 ssh-keygen -t rsa 根据上图中红框标出的id_rsa.pub地址&#xff0c;找到它&#xff0c;使用txt文件打开&#xff0c;复…...

编程日记 2024/8/7 21:52:23

滚珠花键：新能源汽车传动系统的核心动力传递者

在日常生活中&#xff0c;汽车已经成为了必不可少的交通工具&#xff0c;尤其是新能源汽车。而滚珠花键作为传动系统中的重要组成部分&#xff0c;在传动系统方面的作用不容忽视。 随着科技的不断发展&#xff0c;汽车行业也在不断进步&#xff0c;滚珠花键作为高精度的机械传动…...

编程日记 2024/8/7 21:51:22

LeetCode 149, 347, 31

文章目录 149. 直线上最多的点数题目链接标签思路总体思路如何判断 一个点 在 由两点确定的直线 上 代码 347. 前 K 个高频元素题目链接标签思路代码 31. 下一个排列题目链接标签思路代码 149. 直线上最多的点数 题目链接 149. 直线上最多的点数 标签 几何 数组 哈希表 数学…...

编程日记 2024/8/7 21:50:22

操作系统（信号处理）

一、信号介绍 什么是中断&#xff1a; 当进程接收到消息后中止当前正在执行的任务&#xff0c;转而执行其它任务&#xff0c;等待其它任务执行完毕后再返回继续执行。这种执行模式称为中断&#xff0c;分为硬件中断和软件中断两种 什么是信号&#xff1a; 信号是UNIX、类UNI…...

编程日记 2024/8/7 21:49:20

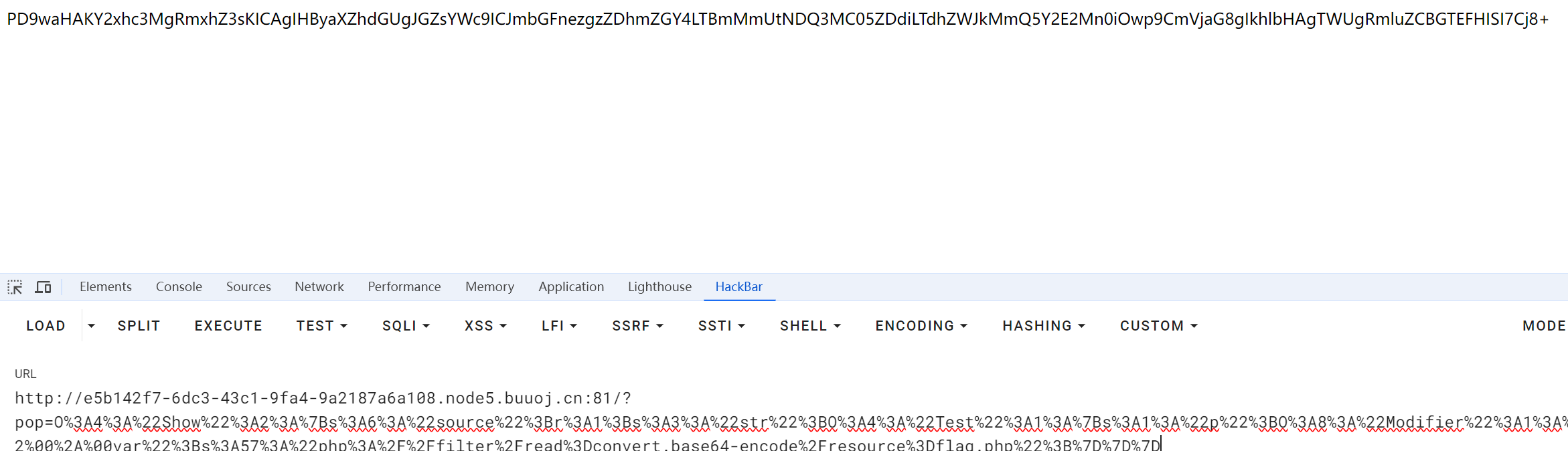
[MRCTF2020]Ezpop

[MRCTF2020]Ezpop 题目是pop&#xff0c;考的其实就是pop链&#xff0c;可以自己先学学&#xff0c;啥也不会QAQ php反序列化之pop链_pop3.phpwelcome-CSDN博客 POP 面向属性编程(Property-Oriented Programing) 常用于上层语言构造特定调用链的方法&#xff0c;与二进制利用…...

编程日记 2024/8/7 21:48:19

24暑假算法刷题 | Day27 | 贪心算法 I | LeetCode 455. 分发饼干，376. 摆动序列，53. 最大子数组和

目录 455. 分发饼干题目描述题解 376. 摆动序列题目描述题解 53. 最大子数组和题目描述题解 455. 分发饼干 点此跳转题目链接 题目描述 假设你是一位很棒的家长&#xff0c;想要给你的孩子们一些小饼干。但是&#xff0c;每个孩子最多只能给一块饼干。 对每个孩子 i&#x…...

编程日记 2024/8/7 21:47:18

Golang 的空接口有什么用？

空接口在 Go 语言中具有多种重要用途&#xff1a; 实现通用的数据结构 例如&#xff0c;可以创建一个包含空接口类型元素的切片或映射&#xff0c;从而能够存储不同类型的值。这在处理多种未知类型的数据时非常有用。比如&#xff0c;一个日志系统可能会将不同类型的日志消息&a…...

编程日记 2024/8/7 21:41:12

计算机毕业设计选题推荐-课程教学平台-Java/Python项目实战

✨作者主页&#xff1a;IT毕设梦工厂✨ 个人简介&#xff1a;曾从事计算机专业培训教学&#xff0c;擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Py…...

编程日记 2024/8/7 21:39:09

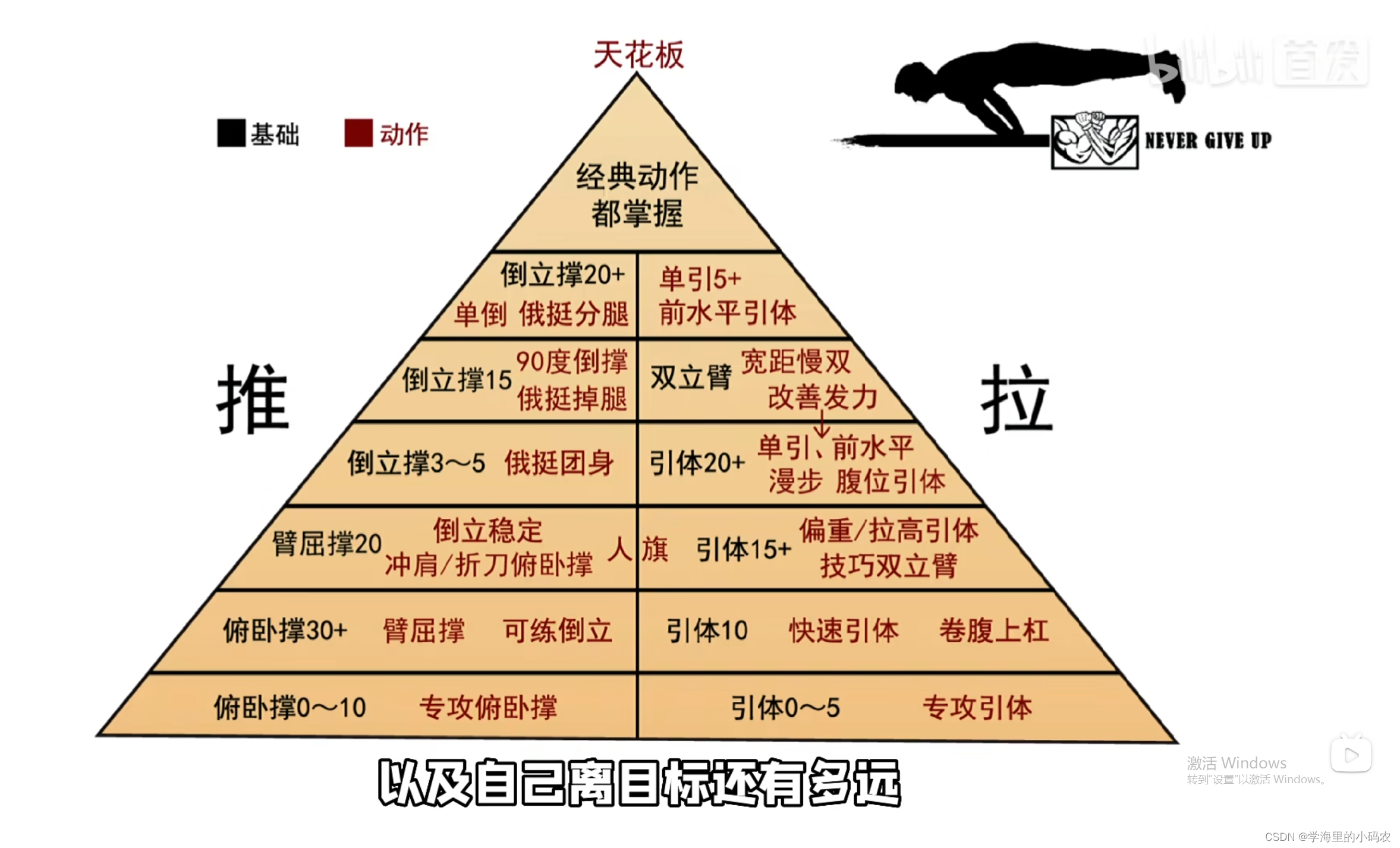
健身日记之倒立俯卧撑学习——起始日2024.6.4

文章目录 目录 前言上期预期 昔日计划 新目标计划 瓶颈突破尝试 参考视频及文章 前言 两个月过去了&#xff0c;已经有所突破了&#xff0c;但是比较预期还是有较大差距&#xff0c;忘记更新csdn了&#xff0c;平时抖音视频号记录的多一些。 上期预期 2024.6.4开始尝试突…...

编程日记 2024/8/7 21:37:08

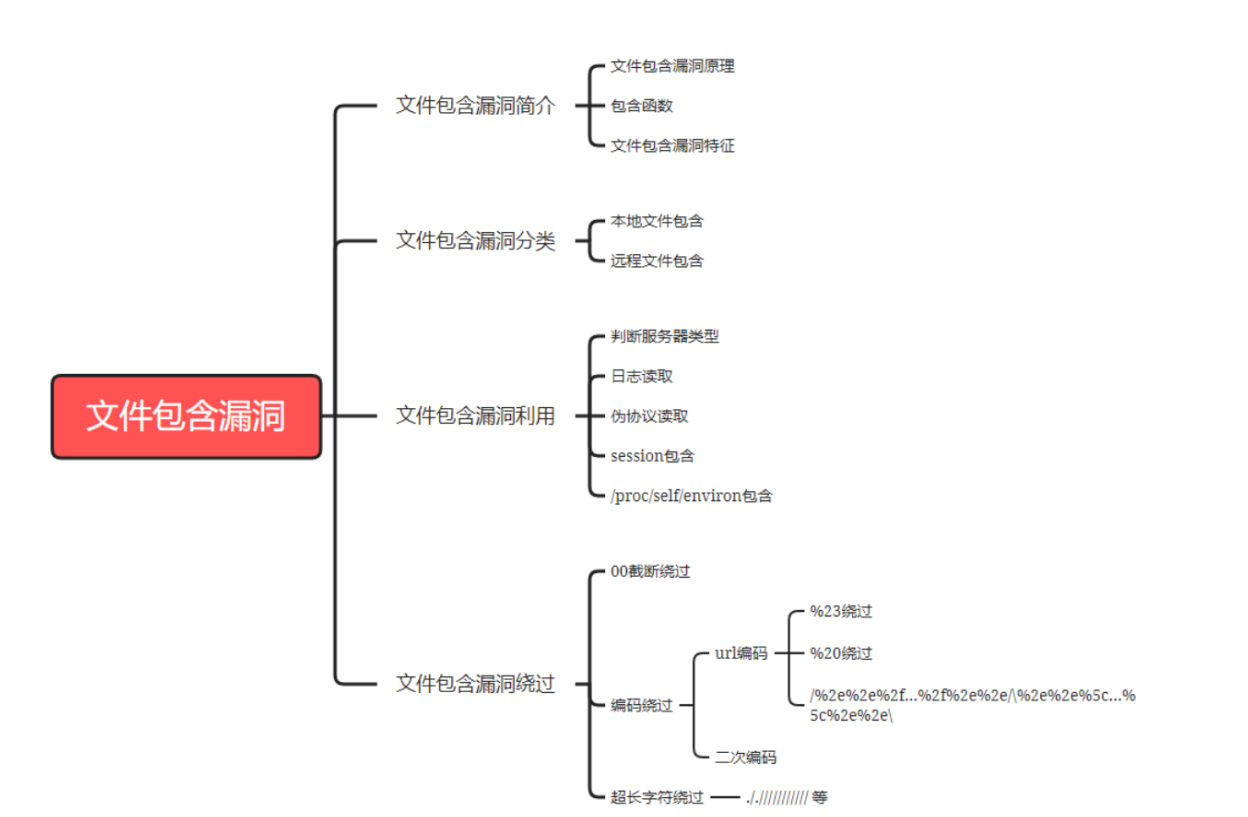
pikachu文件包含漏洞

一&#xff1a;漏洞基础 程序在引用文件的时&#xff0c;引用的文件名存在可控的情况&#xff0c;传入的文件名没有经过合理的校验或校验不严&#xff0c;从而操作了预想之外的文件&#xff0c;就有可能导致文件泄漏和恶意的代码注入&#xff1b; 文件包含漏洞概念 在PHP程序…...

编程日记 2024/8/7 21:35:05

09.FreeRTOS时间片调度与任务相关函数

文章目录 09. FreeRTOS时间片调度与任务相关函数1. FreeRTOS时间片调度2. 任务状态查询API函数3. 任务时间统计API函数 09. FreeRTOS时间片调度与任务相关函数 1. FreeRTOS时间片调度 时间片调度简介&#xff1a; 时间片调度实验流程&#xff1a; 核心代码&#xff1a; 开…...

编程日记 2024/8/7 21:34:04

git分支介绍

git branch 查看当前分支情况 可以看见当前只有一个分支叫main&#xff0c;也就是默认分支&#xff0c;可以理解为树的主干&#xff0c;git早期版本中默认分支叫master 命令行创建一个新分支 git branch [分支名]在创建之后&#xff0c;如果需要切换到新分支需要git switc…...

编程日记 2024/8/7 21:30:59

django filter 统计数量 按属性去重

在Django中&#xff0c;如果你想要根据某个属性对查询集进行去重并统计数量&#xff0c;你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求&#xff1a; 方法1&#xff1a;使用annotate()和Count 假设你有一个模型Item&#xff0c;并且你想…...

编程新知 2026/1/11 2:37:51

学习STC51单片机31（芯片为STC89C52RCRC）OLED显示屏1

每日一言 生活的美好&#xff0c;总是藏在那些你咬牙坚持的日子里。 硬件&#xff1a;OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写&#xff0c;"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

编程新知 2026/1/30 4:16:26

高危文件识别的常用算法：原理、应用与企业场景

高危文件识别的常用算法&#xff1a;原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件&#xff0c;如包含恶意代码、敏感数据或欺诈内容的文档&#xff0c;在企业协同办公环境中&#xff08;如Teams、Google Workspace&#xff09;尤为重要。结合大模型技术&…...

编程新知 2026/2/8 10:51:42

ETLCloud可能遇到的问题有哪些？常见坑位解析

数据集成平台ETLCloud&#xff0c;主要用于支持数据的抽取&#xff08;Extract&#xff09;、转换&#xff08;Transform&#xff09;和加载&#xff08;Load&#xff09;过程。提供了一个简洁直观的界面&#xff0c;以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

编程新知 2026/2/3 12:56:31

Linux-07 ubuntu 的 chrome 启动不了

文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了&#xff0c;报错如下四、启动不了&#xff0c;解决如下 总结 问题原因 在应用中可以看到chrome&#xff0c;但是打不开(说明&#xff1a;原来的ubuntu系统出问题了&#xff0c;这个是备用的硬盘&a…...

编程新知 2026/1/29 17:56:19

企业如何增强终端安全？

在数字化转型加速的今天&#xff0c;企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机&#xff0c;到工厂里的物联网设备、智能传感器&#xff0c;这些终端构成了企业与外部世界连接的 “神经末梢”。然而&#xff0c;随着远程办公的常态化和设备接入的爆炸式…...

编程新知 2026/1/29 9:14:58

PAN/FPN

import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

编程新知 2025/10/20 4:39:36

【笔记】WSL 中 Rust 安装与测试完整记录

#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统&#xff1a;Ubuntu 24.04 LTS (WSL2)架构&#xff1a;x86_64 (GNU/Linux)Rust 版本&#xff1a;rustc 1.87.0 (2025-05-09)Cargo 版本&#xff1a;cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

编程新知 2026/1/26 14:15:48

Webpack性能优化：构建速度与体积优化策略

一、构建速度优化 1、​​升级Webpack和Node.js​​ ​​优化效果​​&#xff1a;Webpack 4比Webpack 3构建时间降低60%-98%。​​原因​​&#xff1a; V8引擎优化&#xff08;for of替代forEach、Map/Set替代Object&#xff09;。默认使用更快的md4哈希算法。AST直接从Loa…...

编程新知 2025/12/26 15:05:09

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用

一、方案背景​ 在现代生产与生活场景中&#xff0c;如工厂高危作业区、医院手术室、公共场景等&#xff0c;人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式&#xff0c;存在效率低、覆盖面不足、判断主观性强等问题&#xff0c;难以满足对人员打手机行为精…...

编程新知 2026/2/7 21:37:35