组合数的低复杂度运算
题源
题目
F. 预期中位数
每次测试的时间限制:3 秒
每次测试的内存限制:256 兆字节
Arul 有一个长度为 n 的二进制数组* a。
他将取该数组中所有长度为 k(k 为奇数)的子序列并找到它们的中位数。
所有这些值的总和是多少?
由于这个和可能非常大,因此输出它对 109° + 7 取模的结果。换句话说,打印该和除以 10° + 7 后的余数。
二进制数组是仅由零和一组成的数组。
† 如果数组 b 可以通过从 a 中删除几个(可能是零个或全部)元素来获得,则数组 b 是数组 a 的子序列。子序列不必是连续的。
奇数长度 k 的数组的中位数是排序后的第 +1 个元素。2
输入第一行包含一个整数 t(1 ≤ t ≤ 104)表示测试用例的数量。
每条测试用例第一行包含两个整数n和k(1≤k≤n≤2105,k为奇数),分别为数组的长度和子序列
每个测试用例的第二行包含 n 个整数 ai (0 < a < 1)——数组的元素。
保证所有测试用例的 n 之和不超过 2.105。
输出
对于每个测试用例,打印模 109 + 7 的总和。
题目分析
基础的组合数问题,不需要多少分析,针对每一种1占据多数的子字符串情况进行组合数目加和就可以主要是算法空间时间复杂度的问题
解答
由于不知道更优时间复杂度的算法+懒,我一直在套用旧的组合数板子
时间空间复杂度都是 O ( n 2 ) 时间空间复杂度都是O(n^2) 时间空间复杂度都是O(n2)
ll Mod;
const ll N = 5e3 + 100;
ll comb[N][N];
auto setMod = [](ll n = 1e9 + 7) {Mod = n;
};
void get_comb(int n) {for (int i = 0; i <= n; i++)for (int j = 0; j <= i; j++)comb[i][j] = (0 < j && j < i) ? (comb[i - 1][j - 1] + comb[i - 1][j]) % Mod : 1;
}
int C(int n, int m) {if (n == m && m == -1) return 1; //* 隔板法特判if (n < m || m < 0) return 0;return comb[n][m];
}
/// 加法递推求组合数,O(n^2),模数非素数时可用
完整代码
新的板子
O ( log n )时间复杂度(如果不看初始化 O ( n ) 的话) O ( n )空间时间复杂度的算法 O(\log n)时间复杂度(如果不看初始化O(n)的话)\newline O(n)空间时间复杂度的算法 O(logn)时间复杂度(如果不看初始化O(n)的话)O(n)空间时间复杂度的算法
ll Mod = 1e9 + 7;
const ll N = 3e5 + 7;auto setMod = [](ll n = 1e9 + 7) {Mod = n;
};//快速幂模板fusk power template
ll qpow(ll a, ll k) {ll ans = 1;while (k) {if (k & 1)ans = 1LL * a * ans % Mod;k >>= 1;a = 1LL * a * a % Mod;}return ans;
}
//组合数模板combination number templatevector<ll> fact(N, 1);
void ini(ll n) {rep(i, 1, n) {fact[i] = (fact[i - 1] * i) % Mod;}
}
ll C(ll n, ll k) {if (n < k)return 0ll;return fact[n] * qpow((fact[n - k] * fact[k]) % Mod, Mod - 2) % Mod;
}相关文章:

组合数的低复杂度运算
题源 题目 F. 预期中位数 每次测试的时间限制:3 秒 每次测试的内存限制:256 兆字节 Arul 有一个长度为 n 的二进制数组* a。 他将取该数组中所有长度为 k(k 为奇数)的子序列并找到它们的中位数。 所有这些值的总和是多少…...

小型并网式光伏气象站:光伏电站的智能守护者
小型并网式光伏气象站以其独特的功能和优势,成为了电站高效运行的智能守护者。小型并网式光伏气象站通过精准的数据采集与分析,为光伏电站的运维管理提供了强有力的支持。 小型并网式光伏气象站能够实时监测并记录光伏电站周围环境的多种气象参数&#x…...
)
JavaScript 中的回调函数(callback)
JavaScript 中的回调函数(callback) JavaScript 中的回调函数(callback)是一个传递给另一个函数作为参数的函数,并且这个传递的函数可以在其他函数内部被调用执行。回调函数是异步编程的一个核心概念,特别…...

计算机毕业设计hadoop+spark+hive漫画推荐系统 动漫视频推荐系统 漫画分析可视化大屏 漫画爬虫 漫画推荐系统 漫画爬虫 知识图谱 大数据
HadoopSparkHive漫画推荐系统详细开题报告 一、引言 随着互联网技术的飞速发展,动漫和漫画产业的数据量急剧增长。用户面临着海量漫画作品的选择难题,如何从这些数据中高效地提取有价值的信息,为用户推荐符合其喜好的漫画作品,成…...

解决pycharm日志总是弹出“无法运行Git,未安装Git”的问题
需求分析 我电脑中安装了git,但是打开pycharm,右下角总是弹出 无法运行Git,未安装Git的日志。 解决方法 首先打开pycharm,按照以下路径,依次点击。 file -----settings-----version control -----Git----Git path(选择自己下载…...

threejs 节点材质系统 绑定attribute
新的 节点材质系统 绑定属性及使用 非常方便 不必重复声明 以instances为例 import {instancedBufferAttribute,instancedDynamicBufferAttribute,} from "three/tsl";声明一个 InstancedBufferAttribute 使用 instancedBufferAttribute包装后就可以在shader中直接使…...

Rabbitmq的几种工作模式
工具类 public class RabbitMQConnection {public static Connection getConnection() throws Exception{//1.创建connectionFactoryConnectionFactory connectionFactory new ConnectionFactory();//2.配置HostconnectionFactory.setHost("127.0.0.1");//3.设置Po…...

如何在 Debian 上安装运行极狐GitLab Runner?【二】
极狐GitLab 是 GitLab 在中国的发行版,专门面向中国程序员和企业提供企业级一体化 DevOps 平台,用来帮助用户实现需求管理、源代码托管、CI/CD、安全合规,而且所有的操作都是在一个平台上进行,省事省心省钱。可以一键安装极狐GitL…...

简单的docker学习 第13章 CI/CD与Jenkins(下)
第13章 CI/CD 与 Jenkins 13.13 自由风格的 CI 操作(最终架构) 前面的架构存在的问题是,若有多个目标服务器都需要使用该镜像,那么每个目标服务器都需要在本地构建镜像,形成系统资源浪费。若能够在 Jenkins 中将镜像相撞构建好并推送到 Har…...
(202))
基于STM32设计的智能鱼缸_带鱼儿数量视觉识别(华为云IOT)(202)
文章目录 一、前言1.1 项目介绍【1】项目功能介绍【2】设计实现的功能【3】项目硬件模块组成1.2 设计思路【1】整体设计思路【2】ESP8266工作模式配置【3】自动换水原理1.3 项目开发背景【1】选题的意义【2】可行性分析【3】参考文献1.4 开发工具的选择【1】设备端开发【2】上位…...

立体连接模式下的传播与沟通:AI智能名片小程序的创新应用与深度剖析
摘要:在数字化浪潮的推动下,信息传播与沟通方式正经历着前所未有的变革。立体连接模式,作为这一变革的重要产物,通过整合物理空间、虚拟网络空间与社群心理空间的三维联动,实现了信息的深度传播与高效互动。AI智能名片…...

基于Python的Scrapy爬虫的个性化书籍推荐系统【Django框架、超详细系统设计原型】
文章目录 有需要本项目的代码或文档以及全部资源,或者部署调试可以私信博主项目介绍系统分析系统设计展示总结 有需要本项目的代码或文档以及全部资源,或者部署调试可以私信博主 项目介绍 近年来,随着互联网的蓬勃发展,企事业单…...

二叉树bst
二叉搜索树的中序遍历结果有序 ,二叉搜索树性质,左小右大,二叉搜索树中序遍历的结果应该是从小到大的。 题目描述二叉树是从上到下,从左到右描述,并非前中后序中的一种。 99. 恢复二叉搜索树 class Solution:first …...

elasticsearch的使用(二)
DSL查询 Elasticsearch的查询可以分为两大类: 叶子查询(Leaf query clauses):一般是在特定的字段里查询特定值,属于简单查询,很少单独使用。 复合查询(Compound query clauses)&am…...

YOLOv8由pt文件中读取模型信息
Pytorch的pt模型文件中保存了许多模型信息,如模型结构、模型参数、任务类型、批次、数据集等 在先前的YOLOv8实验中,博主发现YOLOv8在预测时并不需要指定任务类型,因为这些信息便保存在pt模型中,那么,今天我们便来看看…...

js遍历效率
1w条数据,遍历效率 1、for 15s let t(new Date()).getTime()let a[]for(var i 0; i < 100000; i){a.push({id:i,val:i})}let ts[]for(var i 0; i < a.length; i){if(a[i].val!2 && a[i].val!4 && a[i].val!8){ts.push(a[i])}}let c(new D…...
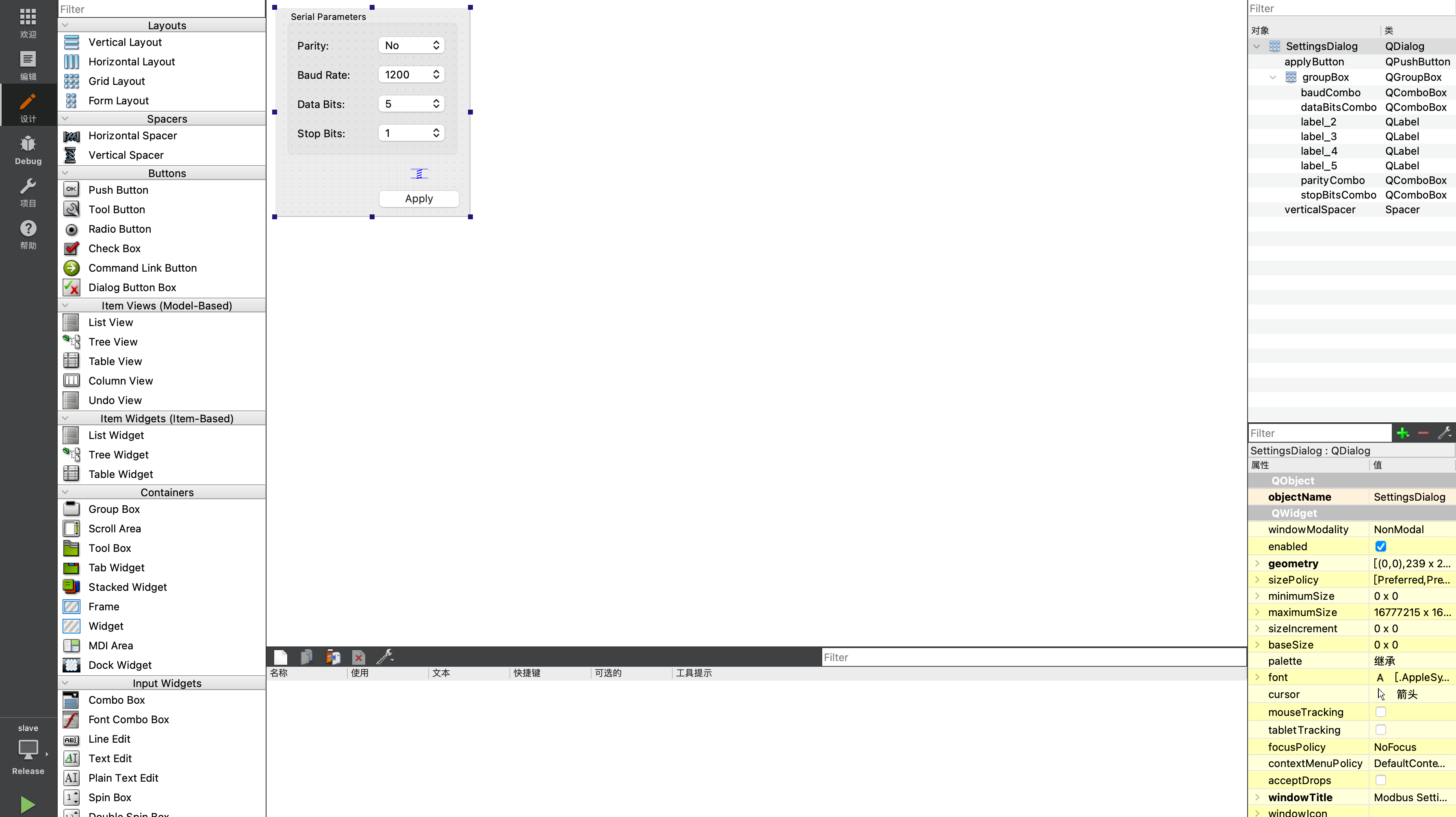
QModbus例程分析
由于有一个Modebus上位机的需要,分析一下QModbus Slave的源代码,方便后面的开发。 什么是Modbus Modbus是一种常用的串行通信协议,被广泛应用于工业自动化领域。它最初由Modicon(目前属于施耐德电气公司)于1979年开发…...

Vue万字学习笔记(入门1)
目录 简介 Vue是什么 渐进式框架 单文件组件 API 风格 选项式 API (Options API) 组合式 API (Composition API) 创建一个 Vue 应用 挂载应用 DOM 中的根组件模板 应用配置 多个应用实例 模板语法 文本插值 原始 HTML Attribute 绑定 简写…...

Cesium手动建模模型用Cesiumlab转3D Tiles模型位置不对,调整模型位置至指定经纬度
Cesium加载3Dtiles模型的平移和旋转_3dtiles先旋转再平移示例-CSDN博客 Cesium 平移cesiumlab生产的3Dtiles切片模型到目标经纬度-CSDN博客 【ArcGISCityEngine】自行制作Lod1城市大尺度白膜数据_cityengine 生成指定坐标集指定区域的白模-CSDN博客 以上次ArcGISCityEngine制…...

学习C语言第23天(程序环境和预处理)
1. 程序的翻译环境和执行环境 在ANSIC的任何一种实现中,存在两个不同的环境 第1种是翻译环境,在这个环境中源代码被转换为可执行的机器指令。 第2种是执行环境,它用于实际执行代码。 2. 详解编译链接 2.1 翻译环境 每个源文件单独经过编…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...
