24/8/8算法笔记 决策树构建鸢尾花
决策树是一种由算法自动设计的模型。在机器学习中,构建决策树的过程通常遵循以下步骤:
-
特征选择:算法会评估每个特征,并选择一个特征作为节点分裂的依据。这个选择基于某种准则,如信息增益(ID3算法)或Gini不纯度(CART算法)。
-
最佳分裂点确定:算法会计算每个特征的所有可能分裂点,并选择一个使得不纯度最小(或信息增益最大)的分裂点。
-
递归分裂:在选择了特征和分裂点后,算法会递归地对数据集的每个子集重复上述过程,直到满足停止条件。
-
停止条件:停止条件可以是多种因素,例如:
- 数据集的不纯度低于某个阈值。
- 达到预设的最大树深度。
- 节点中的样本数量低于某个阈值。
- 没有更多的特征可以用来分裂。
-
剪枝:为了防止过拟合,算法可能会采用剪枝技术来减少树的复杂度。这包括预剪枝(在生长过程中限制树的大小)和后剪枝(先生长整棵树,然后从底部剪除不必要的分支)。
-
输出模型:最终,算法会输出一个决策树模型,该模型可以通过一系列的问题(特征和分裂点)来对新的数据点进行分类。
首先导入库和数据,分割数据集,创建 DecisionTreeClassifier 的实例并使用训练集数据对其进行训练。预测分数
import numpy as np
from sklearn.tree import DecisionTreeClassifier
from sklearn import datasets
import graphviz
from sklearn.model_selection import train_test_split
from sklearn import treeiris = datasets.load_iris()
X = iris['data']
y = iris['target']feature_names = iris['feature_names']X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state =256)model = DecisionTreeClassifier()
model.fit(X_train,y_train)print('测试数据得分',model.score(X_test,y_test))print('算法预测结果',model.predict(X_test))
print('真实结果 ',y_test)

#逻辑斯蒂回归中,手动计算过概率
model.predict_proba(X_test)
构建决策树
dot_data = tree.export_graphviz(model,filled=True,rounded=True,feature_names=feature_names)graphviz.Source(dot_data)
我们可以分析出构建的决策树使用了以下特征和策略:
-
特征选择:决策树使用了鸢尾花数据集中的以下特征:
- petal length (cm):花瓣长度
- petal width (cm):花瓣宽度
- sepal width (cm):萼片宽度
-
分裂准则:决策树的每个节点都基于某个特征的阈值进行分裂,例如 "petal length (cm) <= 2.45" 表示如果花瓣长度小于或等于2.45厘米,则按照这个条件进行数据的分裂。
-
Gini不纯度:每个节点都显示了Gini不纯度值,这是衡量数据集纯度的指标。Gini不纯度越低,表示数据集的纯度越高。例如,一个节点显示 "gini = 0.666" 表示该节点的不纯度较高,而 "gini = 0.0" 表示该节点的样本全部属于同一类别。
-
样本数量:每个节点都显示了该节点下的样本数量,例如 "samples = 120" 表示该节点下有120个样本。
-
类别分布:每个节点都显示了该节点下各个类别的样本数量,例如 "value = [39, 39, 42]" 表示该节点下有39个样本属于第一类,39个样本属于第二类,42个样本属于第三类。
-
递归分裂:决策树通过递归的方式进行分裂,直到满足停止条件,例如Gini不纯度降至0(所有样本属于同一类别)或者达到预设的最大深度。
-
停止条件:当一个节点的Gini不纯度降至0,或者样本数量很少时,分裂会停止。例如,"gini = 0.0" 表示该节点下的所有样本都属于同一类别,不需要进一步分裂。
-
特征重要性:从截图中可以看出,花瓣长度和宽度的特征在多个节点中被用作分裂准则,这表明这些特征对于分类可能更为重要。
-
树的深度:从截图中可以看出,树的深度相对较浅,这意味着模型可能没有过拟合,但也可能没有捕捉到数据的所有特征。
-
预测结果:最终,每个叶节点都会给出一个预测结果,通常是多数投票的结果。
相关文章:

24/8/8算法笔记 决策树构建鸢尾花
决策树是一种由算法自动设计的模型。在机器学习中,构建决策树的过程通常遵循以下步骤: 特征选择:算法会评估每个特征,并选择一个特征作为节点分裂的依据。这个选择基于某种准则,如信息增益(ID3算法…...

数据库扩展新篇章:主流分库分表中间件全解析
摘要: 随着企业数据量的激增,传统的单体数据库架构已经无法满足日益增长的性能需求和数据管理复杂性。分库分表技术作为解决这一问题的有效手段,通过将数据水平或垂直地分散到多个数据库中,提高了系统的扩展性和处理能力。本文将详…...

python看图片猜价格游戏,frame 和PhotoImage的使用
import tkinter.messagebox import tkinter import randomwindow tkinter.Tk()window.geometry(800x400)window.title(猜数字游戏)good_price random.randint(10, 100) input_price random.randint(1, 100)def sumit():global good_priceif entry.get() "" or en…...

未来展望:等保测评在网络安全领域的持续创新与发展
在数字化浪潮席卷全球的今天,网络安全已成为维护国家安全、社会稳定和经济发展的关键基石。作为网络安全保障体系的核心组成部分,等级保护测评(简称“等保测评”)在应对日益复杂多变的网络威胁中发挥着不可替代的作用。展望未来&a…...

构建深度学习驱动的多目标检测系统:YOLO模型及应用
随着计算机视觉技术的飞速发展,多目标检测在各种实际应用中发挥着越来越重要的作用。本文将j简单介绍如何构建一个基于深度学习的多目标检测系统,包括数据准备、模型训练、UI界面开发和部署的完整流程。如有部署的想法,想要(UI界面…...
)
算法刷题笔记 染色法判定二分图(染色法例题 C++实现)
文章目录 题目描述二分图介绍和基本思路实现代码(C) 题目描述 给定一个n个点m条边的无向图,图中可能存在重边和自环。请你判断这个图是否是二分图。 输入格式 第一行包含两个整数n和m。接下来m行,每行包含两个整数u和v…...

在Ubuntu上安装OpenBLAS和Eigen
安装 openblas 直接使用 apt-get 命令即可安装: sudo apt-get install libopenblas-dev检查是否安装成功,可以用下面的示例代码 example.cpp: #include <stdio.h> #include <stdlib.h> #include "cblas.h"int main(…...
)
Vue前端面试基础(一)
Vue面试题目详解可以涵盖多个方面,从基础知识到高级特性,再到实际应用和性能优化等。以下是一些常见的Vue面试题目及其详解: 1. Vue双向绑定原理 详解: Vue的双向绑定原理是通过数据劫持结合发布者-订阅者模式实现的。Vue在内部…...
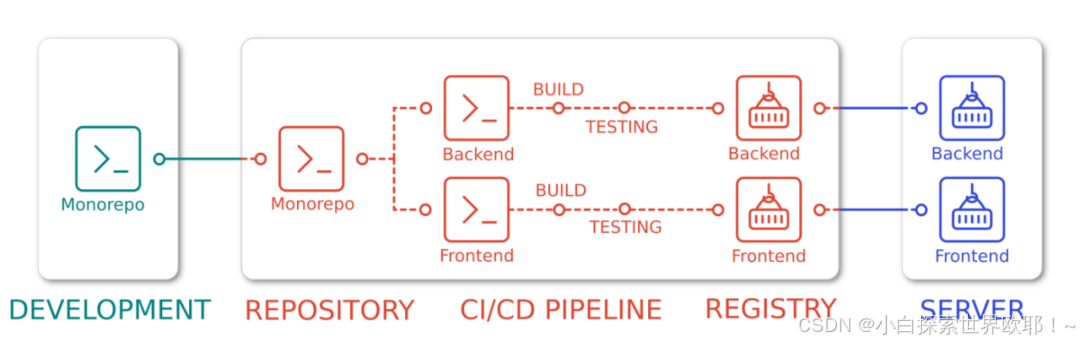
使用Gitlab实现monorepo多项目CICD
CI/CD是什么 CI/CD(Continuous Intergration/Continuous Delpoy),即持续集成/持续部署,或称为持续集成/持续交付,作为一套面向开发和运维团队的解决方案,CI/CD 主要解决集成新代码和向用户频繁交付应用的问…...

设计模式实战:银行账户管理系统的设计与实现
问题描述 设计一个银行账户管理系统,支持不同类型的账户(如储蓄账户、支票账户)进行存取款操作,并能够在账户余额发生变化时通知相关观察者(如用户、银行系统)。系统需要确保账户操作的灵活性和可扩展性。 设计分析 策略模式 策略模式定义了一系列算法,并将每个算法…...

⭕️【论文阅读】《Interactive Class-Agnostic Object Counting》
[2309.05277] Interactive Class-Agnostic Object Counting (arxiv.org) code: cvlab-stonybrook/ICACount: [ICCV23] Official Pytorch Implementation of Interactive Class-Agnostic Object Counting (github.com) 目录 Abstract Abstract 我们提出了一个新…...

高效的编程学习方法和技巧
编程小白如何成为大神?大学新生的最佳入门攻略 编程已成为当代大学生的必备技能,但面对众多编程语言和学习资源,新生们常常感到迷茫。如何选择适合自己的编程语言?如何制定有效的学习计划?如何避免常见的学习陷阱&…...

sublime text插件开发
手工开发了一些ST的py插件,记录过程中遇到的一些问题。 ST3/ST4 begin_edit问题 报错: begin_edit() missing 2 required positional arguments: edit_token and cmdST3时已经不能直接调view.begin_edit方法了,需要通过runCommandTextComm…...

【Linux网络】网络层协议:IP
本篇博客整理了 TCP/IP 分层模型中网络层的 IP 协议,旨在让读者更加深入理解网络协议栈的设计和网络编程。 目录 一、网络层 二、IP 报头 1)报头与有效载荷的分离 2)有效载荷的上交 3)源 IP 与目的 IP 4)生存时间…...

分布式接口文档聚合,Solon 是怎么做的?
1、分布式接口文档聚合,是什么? 如果你有 “22” 个不同的服务(比如微服务),每个服务都有自己的接口文档。每个服务的文档各自打开,估计你会觉得很麻烦的? 再如果,它们是用 openap…...
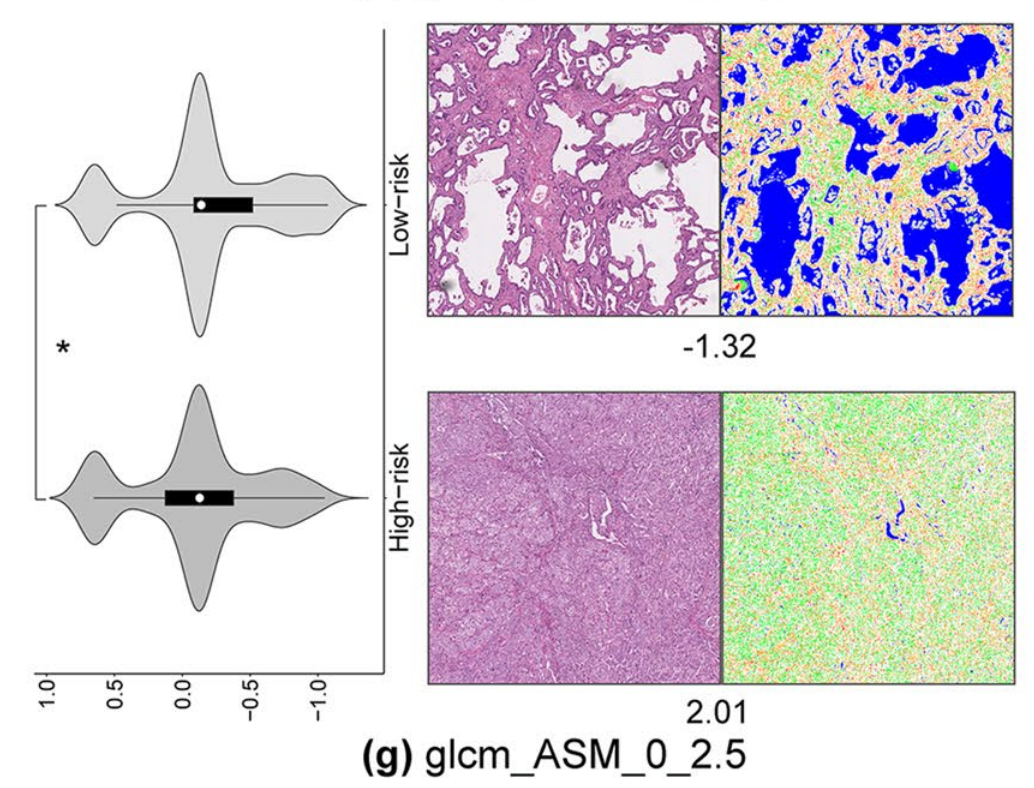
多尺度病理图像纹理特征作为肺腺癌预后预测的新指标|文献精读·24-08-09
小罗碎碎念 这一期推文分享的文献是2022年发表于 Journal of Translational Medicine 的一篇文章,目前IF6.1。 这篇文章值得刚入门病理AI领域的老师/同学仔细研读,因为思路清晰,该讲到的流程基本都涉及了,详细讲述了病理图像的各种…...

RAG+Agent项目实践系列:基于本地菜谱知识库的大语言模型RAG+Agent的解决方案设计和实现
RAG+Agent项目实践系列:基于本地菜谱知识库的大语言模型RAG+Agent的解决方案设计和实现 为 A 项目构建一个基于菜谱知识库的问答机器人,由业务方提供一系列菜谱知识库和公司概况介绍材料,根据这些知识库要求实现一个问答机器人: 实现用户对于机器人自我身份和公司情况的回…...

JupyterNotebook添加Anaconda中已有的虚拟环境
比如,在Acaconde中存在一个我已经配置好的虚拟环境pose,现在我想在Jupyter中使用它 那么可以使用ipython kernel install --user --name 你要添加的环境 添加到Jupyter中。 对于Jupyter中已有的代码,就可以在Kernel - chanage kernel中改变内核。...

利用vscode-icons-js在Vue3项目中实现文件图标展示
背景: 在开发文件管理系统或类似的项目时,我们常常需要根据文件类型展示对应的文件图标,这样可以提高用户体验。本文将介绍如何在Vue3项目中利用vscode-icons-js库,实现类似VSCode的文件图标展示效果。 先看效果: 一…...

某赛通电子文档安全管理系统 CDGAuthoriseTempletService1 SQL注入漏洞复现(XVE-2024-19611)
0x01 产品简介 某赛通电子文档安全管理系统(简称:CDG)是一款电子文档安全加密软件,该系统利用驱动层透明加密技术,通过对电子文档的加密保护,防止内部员工泄密和外部人员非法窃取企业核心重要数据资产,对电子文档进行全生命周期防护,系统具有透明加密、主动加密、智能…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...
