数字信号处理2: 离散信号与系统的频谱分析
文章目录
- 前言
- 一、实验目的
- 二、实验设备
- 三、实验内容
- 四、实验原理
- 五、实验步骤
- 1.序列的离散傅里叶变换及分析
- 2.利用共轭对称性,设计高效算法计算2个N点实序列的DFT。
- 3.线性卷积及循环卷积的实现及二者关系分析
- 4.比较DFT和FFT的运算时间
- 5.利用FFT求信号频谱及分析采样频率、噪声对频谱的影响
- 6.创新训练拓展内容
- 6.1 信号持续时间、频谱分析范围、采样点数和谱分辨率的关系。
- 6.2频谱的内插函数恢复(频域采样恢复)
- 6.3对语音信号进行简单分析。
- 六、实验结论与心得体会(手写)
- 七、实验参考资料
前言
本人初次学习离散信号与系统的频谱分析。
一、实验目的
1.掌握离散傅里叶变换(DFT)及快速傅里叶变换(FFT)的计算机实现方法。
2.检验序列DFT的性质。
3.掌握利用DFT(FFT)计算序列线性卷积的方法。
4.学习用DFT对连续信号和时域离散信号进行谱分析的方法,了解可能出现的分析误差,以便在实际中正确应用DFT。
5.了解采样频率对谱分析的影响。
6.了解利用FFT进行语音信号分析的方法。
二、实验设备
1.计算机
2.Matlab软件2014a以上版本。
三、实验内容
1.对不同序列进行离散傅里叶变换并进行分析;DFT共轭对称性质的应用(通过1次N点FFT计算2个N点实序列的DFT)。
2.线性卷积及循环卷积的关系,以及利用DFT(FFT)进行线性卷积的方法。
3.比较计算序列的DFT和FFT的运算时间。
4.利用FFT实现带噪信号检测。
5.利用FFT计算信号频谱。
6.扩展部分主要是关于离散系统采样频率、时域持续时间、谱分辨率等参数之间的关系,频谱的内插恢复,对语音信号进行简单分析。
四、实验原理
1.序列的离散傅里叶变换及性质
2.利用DFT计算线性卷积
3.利用DFT对信号进行谱分析
4.DFT和FFT的运算量
5.信噪比
五、实验步骤
1.序列的离散傅里叶变换及分析
分别对复序列,实序列,实偶序列,实奇序列,虚奇序列进行离散傅里叶变换,得到实验结果并对其特点进行分析。实验所需序列自选。
解:A、设定复序列:x(n)= {1,1,1,1,1}+j*{1,2,3,4,5} ;实序列:x1(n)= {1,1,1,1,1}
程序:
x1=ones(1,5);
x2=1:5;
x=x1+j*x2;
y1=fft(x,10);
y2=fft(x1,10);
subplot(1,2,1)
stem(0:9,abs(y1),'filled');
title('复序列DFT的幅度谱');
subplot(1,2,2)
stem(0:9,abs(y2),'filled');
title('实序列DFT的幅度谱');
结果:

B、设定实偶序列:x(n)= {5,4,3,2,1,0,1,2,3,4},实奇序列:x(n)= {0,4,3,2,1,0,-1,-2,-3,-4},虚奇序列:x(n)= j*{0,4,3,2,1,0,-1,-2,-3,-4};
程序:
x=[5,4,3,2,1,0,1,2,3,4];
y=fft(x,10);
subplot(3,3,1)
stem(0:9,abs(y),'filled');
title('实偶序列DFT的幅度谱');
subplot(3,3,2)
stem(0:9,real(y),'filled');
title('实偶序列DFT的实部');
subplot(3,3,3)
stem(0:9,imag(y),'filled');
title('实偶序列DFT的虚部');
x=[0,4,3,2,1,0,-1,-2,-3,-4];
y=fft(x,10);
subplot(3,3,4)
stem(0:9,abs(y),'filled');
title('实奇序列DFT的幅度谱');
subplot(3,3,5)
stem(0:9,real(y),'filled');
title('实奇序列DFT的实部');
subplot(3,3,6)
stem(0:9,abs(imag(y)),'filled');
title('实奇序列DFT的虚部');
x=j*[0,4,3,2,1,0,-1,-2,-3,-4];
y=fft(x,10);
subplot(3,3,7)
stem(0:9,y,'filled');
title('虚奇序列DFT的幅度谱');
subplot(3,3,8)
stem(0:9,real(y),'filled');
title('虚奇序列DFT的实部');
subplot(3,3,9)
stem(0:9,imag(y),'filled');0
title('虚奇序列DFT的虚部');
结果:

分析:

2.利用共轭对称性,设计高效算法计算2个N点实序列的DFT。
用一个N点FFT计算两个长度为N的实序列N点离散傅里叶变换,并将结果和直接使用两个N点DFT得到的结果进行比较。
解:设定 x 1 ( n ) x_1 (n) x1(n)={1,2,3,4,5,6},0≤n≤5; x 2 ( n ) x_2 (n) x2(n)={1,2,1,3,1,4},0≤n≤5;
程序:
x1=[1,2,3,4,5,6];
x2=[1,2,1,3,1,4];
y1=fft(x1);
y2=fft(x2);
x=x1+j*x2;
y=fft(x,6);
[xec,xoc]=circevod(y);
subplot(2,2,1)
stem(0:5,abs(y1),'filled');
title('x_1(n)的直接六点DFT的幅度谱');
grid on;
subplot(2,2,2)
stem(0:5,abs(y2),'filled');
title('x_2(n)的直接六点DFT的幅度谱');
grid on;
subplot(2,2,3)
stem(0:5,abs(xec),'filled');
title('x_1(n)高效算法DFT的幅度谱');
grid on;
subplot(2,2,4)
stem(0:5,abs(xoc),'filled');
title('x_2(n)高效算法DFT的幅度谱');
grid on;
结果:

分析:

3.线性卷积及循环卷积的实现及二者关系分析
计算两序列的线性卷积及循环卷积,循环卷积采用2种计算方法(时域、频域方法)。设序列x1长度为M,序列x2长度为N,循环卷积长度为L,分别计算L大于、等于、小于(M+N-1)时的循环卷积。序列x1、x2、L自选,得到实验结果并对线性卷积及循环卷积的关系进行分析。
解:设定 x 1 ( n ) x_1 (n) x1(n)={1,2,3,4},0≤n≤5; x 2 ( n ) x_2 (n) x2(n)={1,2,1,3},0≤n≤5;其中M=N=4,分别采用2种方法(时域、频域)计算L=4/7/12的循环卷积
程序:
figure(1)
x1=[1,2,3,4];
x2=[1,2,1,3];
subplot(3,2,1)
y1=circonv(x1,x2,4);
stem(0:3,abs(y1),'filled');
title('从时域计算4点循环卷积');
grid on;
subplot(3,2,3)
y1=circonv(x1,x2,7);
stem(0:6,abs(y1),'filled');
title('从时域计算7点循环卷积');
grid on;
subplot(3,2,5)
y1=circonv(x1,x2,12);
stem(0:11,abs(y1),'filled');
title('从时域计算12点循环卷积');
grid on;
subplot(3,2,2)
y1=fft(x1,4);
y2=fft(x2,4);
x=ifft(y1.*y2)
stem(0:3,abs(x),'filled');
title('从频域计算4点循环卷积');
grid on;
subplot(3,2,4)
y1=fft(x1,7);
y2=fft(x2,7);
x=ifft(y1.*y2)
stem(0:6,abs(x),'filled');
title('从频域计算7点循环卷积');
grid on;
subplot(3,2,6)
y1=fft(x1,12);
y2=fft(x2,12);
x=ifft(y1.*y2)
stem(0:11,abs(x),'filled');
title('从频域计算12点循环卷积');
grid on;figure(2)
x1=[1,2,3,4];
x2=[1,2,1,3];
y=conv(x1,x2);
stem(0:6,y,'filled')
grid on;
title('线性卷积的结果');
结果:


分析:

4.比较DFT和FFT的运算时间
(1)自行选择进行计算的序列(或产生随机序列)。
(2)DFT点数N分别取64、256、1024、2048、……
(3)分别采用直接计算(按DFT定义计算)和fft函数计算,利用计时函数tic、toc,分别统计直接计算和fft计算所用的时间,并对结果进行比较(含直接计算和fft计算的比较、不同点数N所需计算时间和节约时间的比较等)。
解:设定序列为x=[1,2,3,4,ones(1,60)]
程序:
x=[1,2,3,4,ones(1,60)];
tic
X1=dft(x,64);
toc
tic
X2=fft(x,64);
toc
时间已过 0.003188 秒。
时间已过 0.001967 秒。
x=[1,2,3,4,ones(1,252)];
tic
X1=dft(x,256);
toc
tic
X2=fft(x,256);
toc
时间已过 0.012424 秒。
时间已过 0.002118 秒。
x=[1,2,3,4,ones(1,1020)];
tic
X1=dft(x,1024);
toc
tic
X2=fft(x,1024);
toc
时间已过 0.249468 秒。
时间已过 0.008443 秒。
x=[1,2,3,4,ones(1,2044)];
tic
X1=dft(x,2048);
toc
tic
X2=fft(x,2048);
toc
时间已过 1.078018 秒。
时间已过 0.021545 秒
结果:
点数 DFT FFT
64 0.003188 秒 0.001967 秒
256 0.012424 秒 0.002118 秒
1024 0.249468 秒 0.008443 秒
2048 1.078018 秒 0.021545 秒
结果:
| 点数 | DFT | FFT |
|---|---|---|
| 64 | 0.003188 秒 | 0.001967 秒 |
| 256 | 0.012424 秒 | 0.002118 秒 |
| 1024 | 0.249468 秒 | 0.008443 秒 |
| 2048 | 1.078018 秒 | 0.021545 秒 |
分析:

5.利用FFT求信号频谱及分析采样频率、噪声对频谱的影响
(1)设模拟信号 x ( t ) = 3 c o s ( 8 π t ) + 6 c o s ( 20 π t ) x(t)=3 cos( 8πt)+6 cos( 20πt) x(t)=3cos(8πt)+6cos(20πt),以 t = 0.01 n , 0 ≤ n ≤ N − 1 t=0.01n,0≤n≤N-1 t=0.01n,0≤n≤N−1进行采样离散化,画出所得序列 x N ( n ) x_N (n) xN(n)的N点DFT幅值谱(N分别取50,256),利用FFT实现。分析信号频谱所对应频率轴的数字频率和频率之间的关系。在点数N不变的条件下降低采样频率(需满足采样定理),观察信号频谱的变化,分析产生变化的原因。
解:A、采样频率为100hz,分别画出N=50,256点DFT幅度谱如下所示:
程序:
N=50;
n=0:N-1;
T=0.01;
x=3*cos(8*pi*n*T)+6*cos(20*pi*n*T);
subplot(2,2,1);
stem(n,x,'.');
title('f_s=100hz,N=50时的信号');
Y=fft(x,N);
k1=0:N-1;w1=2*pi/N*k1;
subplot(2,2,2);
stem(n,abs(Y),'.');
title('f_s=100hz,N=50时信号的频谱');
N=256;
n=0:N-1;
T=0.01;
x=3*cos(8*pi*n*T)+6*cos(20*pi*n*T);
subplot(2,2,3);
stem(n,x,'.');
title('f_s=100hz,N=256时的信号');
Y=fft(x,N);
k1=0:N-1;w1=2*pi/N*k1;
subplot(2,2,4);
stem(n,abs(Y),'.');
title('f_s=100hz,N=256时信号的频谱')
结果:

B、采样频率为50hz,分别画出N=50,256点DFT幅度谱如下所示:
程序:
N=50;
n=0:N-1;
T=0.02;
x=3*cos(8*pi*n*T)+6*cos(20*pi*n*T);
subplot(2,2,1);
stem(n,x,'.');
title('f_s=50hz,N=50时的信号');
Y=fft(x,N);
k1=0:N-1;w1=2*pi/N*k1;
subplot(2,2,2);
stem(n,abs(Y),'.');
title('f_s=50hz,N=50时信号的频谱');
N=256
n=0:N-1;
T=0.02;
x=3*cos(8*pi*n*T)+6*cos(20*pi*n*T);
subplot(2,2,3);
stem(n,x,'.');
title('f_s=50hz,N=256时的信号');
Y=fft(x,N);
k1=0:N-1;w1=2*pi/N*k1;
subplot(2,2,4);
stem(n,abs(Y),'.');
title('f_s=50hz,N=256时信号的频谱');
结果:

分析:

(2)对序列 x N ( n ) x_N (n) xN(n)(N任取50或者256,需表示为行向量)加入噪声 ( 0.2 ∗ r a n d n ( 1 , N ) ) (0.2*randn(1,N)) (0.2∗randn(1,N)),比较有无噪声时的信号谱,加大噪声到 2 ∗ r a n d n ( 1 , N ) 2*randn(1,N) 2∗randn(1,N)和 10 ∗ r a n d n ( 1 , N ) 10*randn(1,N) 10∗randn(1,N),计算信噪比,画出并比较不同噪声下时域波形和幅度频谱,讨论噪声对信号分析的影响。
答:程序:
figure(1)
N=50;
n=0:N-1;
t=0.01*n;
q=n*2/N;
x1=3*cos(8*pi*t)+6*cos(20*pi*t);
subplot(2,2,1)
plot(n,x1);title('Pure signal')
y=fft(x1,N);
subplot(2,2,2)
plot(q,abs(y));title('FFT of pure signal(N=50)')
x2=x1+0.2*randn(1,N);
SNR1=snr(x1,x2)
subplot(2,2,3)
plot(n,x2);title('noisy signal')
y=fft(x2,N);
subplot(2,2,4)
plot(q,abs(y));title('FFT of signal with noise (N=50)')figure(2)
N=50;
n=0:N-1;
t=0.01*n;
q=n*2/N;
x1=3*cos(8*pi*t)+6*cos(20*pi*t);
x2=x1+2*randn(1,N);
x3=x1+10*randn(1,N);
SNR2=snr(x1,x2)
SNR3=snr(x1,x3)
subplot(2,2,1)
plot(n,x2);title('noisy signal(2*randn(1,N))')
y2=fft(x2,N);
subplot(2,2,2)
plot(q,abs(y2));title('FFT of signal with more noise (N=50)')
subplot(2,2,3)
plot(n,x3);title('noisy signal(10*randn(1,N))')
y3=fft(x3,N);
subplot(2,2,4)
plot(q,abs(y3));title('FFT of signal with more
noise(N=50)') SNR1 =0.0783
SNR2 =-0.6612
SNR3 =-6.4308
图形结果:


分析:

6.创新训练拓展内容
6.1 信号持续时间、频谱分析范围、采样点数和谱分辨率的关系。
(1)已知模拟信号 x ( t ) = c o s ( 200 π t ) + c o s ( 800 π t ) + c o s ( 816 π t ) + c o s ( 1000 π t ) x(t)=cos( 200πt)+cos( 800πt)+cos( 816πt)+cos( 1000πt) x(t)=cos(200πt)+cos(800πt)+cos(816πt)+cos(1000πt),欲采用数字方法分析该信号的频谱,要求能明确区分该信号的所有频率分量(两个相邻频谱分量之间至少间隔一个离散频率点)。为了便于采用基2-FFT来分析该信号的频谱并避免频谱失真,希望截取该信号的整数个周期进行频谱分析,并且采样点数为2M(M为正整数),请确定适当的采样频率(不发生频谱混叠且满足前述要求的最低采样频率)、采样点数(时域最小记录时间),并利用所确定的参数编写程序,对该信号进行频谱分析,画出模拟信号的幅度频谱,分析其频谱分析范围和谱分辨率。
解: f s m i n = 1024 h z , N m i n = 256 f_{smin}=1024hz,N_{min}=256 fsmin=1024hz,Nmin=256(具体过程在下面分析里)
程序
T=1/1024;
n=0:255;
t=n*T;
x=cos(200*pi*t)+cos(800*pi*t)+cos(816*pi*t)+cos(1000*pi*t);
subplot(2,1,1);
stem(n,x,'.')
title('采样1024hz的信号');
axis([0,256,0,4])
subplot(2,1,2);
XK2=fft(x);
w=[0:5000]*pi/5000;
N=256;k=n;
X2=XK2/N*(sin(w*N/2-pi*k')./sin(w/2-pi*k'/N)).*exp(-j*w*(N-1)/2);
plot(w/pi*512,abs(X2))
xlabel('hz');
title('采样1024hz的幅度谱(N=256)');
axis([0,512,0,150])
结果:

分析:

(2)保持采样点数不变,采样频率增大1倍,重新分析信号的幅度频谱。比较信号幅度频谱、谱分辨率、频谱分析范围的变化并分析其原因。
解:程序:
T=1/2048;
n=0:255;
t=n*T;
x=cos(200*pi*t)+cos(800*pi*t)+cos(816*pi*t)+cos(1000*pi*t);
subplot(2,1,1);
stem(n,x,'.')
title('采样2048hz的信号');
axis([0,256,0,4])
subplot(2,1,2);
XK2=fft(x);
w=[0:5000]*pi/5000;
N=256;k=n;
X2=XK2/N*(sin(w*N/2-pi*k')./sin(w/2-pi*k'/N)).*exp(-j*w*(N-1)/2);
plot(w/pi*1024,abs(X2))
xlabel('hz');
title('采样2048hz的幅度谱(N=256)');
axis([0,1024,0,180])
结果:

分析:

(3)保持采样频率不变,分别将采样点数增大和减少1倍,重新分析信号的幅度频谱。比较信号幅度频谱、谱分辨率、频谱分析范围的变化并分析其原因。
解:程序:
T=1/1024;
n=0:127;
t=n*T;
x=cos(200*pi*t)+cos(800*pi*t)+cos(816*pi*t)+cos(1000*pi*t);
subplot(2,2,1);
stem(n,x,'.')
title('采样1024hz的信号');
axis([0,128,0,4])
subplot(2,2,2);
XK2=fft(x);
w=[0:5000]*pi/5000;
N=128;k=n;
X2=XK2/N*(sin(w*N/2-pi*k')./sin(w/2-pi*k'/N)).*exp(-j*w*(N-1)/2);
plot(w/pi*512,abs(X2))
xlabel('hz');
title('采样1024hz的幅度谱(N=128)');
axis([0,512,0,85])
T=1/1024;
n=0:511;
t=n*T;
x=cos(200*pi*t)+cos(800*pi*t)+cos(816*pi*t)+cos(1000*pi*t);
subplot(2,2,3);
stem(n,x,'.')
title('采样1024hz的信号');
axis([0,512,0,4])
subplot(2,2,4);
XK2=fft(x);
w=[0:5000]*pi/5000;
N=512;k=n;
X2=XK2/N*(sin(w*N/2-pi*k')./sin(w/2-pi*k'/N)).*exp(-j*w*(N-1)/2);
plot(w/pi*512,abs(X2))
xlabel('hz');
title('采样1024hz的幅度谱(N=512)');
axis([0,512,0,300])
结果:

分析:

6.2频谱的内插函数恢复(频域采样恢复)
基于频域采样X(k)及内插公式(教材式(3.3.7)和式(3.3.8)),用Matlab编程实现离散谱(DFT)到连续谱的转换:采用N=4的矩形序列 x ( n ) = R 4 ( n ) x(n)=R_4 (n) x(n)=R4(n),分别求出其4点和8点DFT,然后利用内插公式(为保证恢复得到的频谱曲线足够光滑,在Matlab程序中对连续变量ω的离散化,应取200个离散点以上),分别由其4点和8点DFT恢复其连续频谱 X ( e j ω ) X(e^{jω}) X(ejω),画出 X ( e j ω ) X(e^{jω}) X(ejω)的幅度频谱图(应为光滑连续曲线),并比较不同DFT点数恢复的结果以及 R 4 ( n ) R_4 (n) R4(n)的理论频谱(参见教材图2.2.1)。
解:程序:
subplot(2,2,1)
x=[1,1,1,1];
XK1=fft(x,4);
k=0:3;N=4;
w=[-2000:2000]*pi/1000;
X1=XK1/N*(sin(w*N/2-pi*k')./sin(w/2-pi*k'/N)).*exp(-j*w*(N-1)/2);
plot(w/pi,abs(X1))
title('N=4的DFT内插公式恢复结果');
xlabel('w/π');
subplot(2,2,2)
n=0:3;
x=(1).^n;
w=[-500:500]*pi/250;
X=x*exp(-j*n'*w);
plot(w/pi,abs(X))
title('N=4的DFT的理论频谱');
xlabel('w/π');
subplot(2,2,3)
x=[1,1,1,1];
XK2=fft(x,8);
k=0:7;N=8;
w=[-2000:2000]*pi/1000;
X2=XK2/N*(sin(w*N/2-pi*k')./sin(w/2-pi*k'/N)).*exp(-j*w*(N-1)/2);
plot(w/pi,abs(X2))
title('N=8的DFT内插公式恢复结果');
xlabel('w/π');
subplot(2,2,4)
n=0:3;
x=(1).^n
w=[-500:500]*pi/250;
X=x*exp(-j*(0:7)'*w);
plot(w/pi,abs(X))
title('N=8的DFT的理论频谱');
xlabel('w/π');
结果:

分析:

6.3对语音信号进行简单分析。
基于MATLAB平台,利用DFT对以适当的采样频率进行采集的不同人的单音节语音信号进行频谱分析(注意首先要对采集到的语音信号进行适当的截取),画出语音信号的波形及频谱。说明该频谱所对应的模拟频率,分析语音信号的频率分布特点,对比不同人说同一个音节的频谱的差异(最好分别用男声和女声进行分析)。对语音信号波形、单音节语音信号的截取方式、DFT频谱、频谱分析结果等进行讨论。
解:程序:
figure(1)
recObj = audiorecorder;
disp('Start speaking.')
recordblocking(recObj, 2);
disp('End of Recording.');
play(recObj);
y = getaudiodata(recObj);
subplot(1,2,1);
stem(y,'.');
xlabel('时间');
ylabel('幅度');
title('信号波形');
subplot(1,2,2);
stem(abs(fft(y)),'.');
title('信号频谱');
xlabel('频率');
ylabel('幅度');figure(2)
sec1=5
sec2 =12
y1=y(((1000*sec1+1):1000*sec2),:);
subplot(1,2,1);
stem(y1,'.');
xlabel('时间');
ylabel('幅度');
title('适当截取后信号的波形');
subplot(1,2,2);
stem(abs(fft(y1)),'.');
title('适当截取后信号的频谱');
xlabel('频率');
ylabel('幅度');
结果:


分析:

六、实验结论与心得体会(手写)

七、实验参考资料
1.高西全,丁玉美.数字信号处理[M].西安:西安电子科技大学出版社,2008
2.张德丰.详解MATLAB 数字信号处理[M].北京:电子工业出版社,2010
3.王月明,张宝华.MATLAB基础与应用教程[M].北京:北京大学出版社,2012
4.陈怀琛.数字信号处理教程:MATLAB释义与实现(第3版)[M].北京:电子工业出版社,2013
5.宋知用.MATLAB数字信号处理85个实用案例精讲:入门到进阶[M].北京:北京航空航天大学出版社,2016
相关文章:

数字信号处理2: 离散信号与系统的频谱分析
文章目录 前言一、实验目的二、实验设备三、实验内容四、实验原理五、实验步骤1.序列的离散傅里叶变换及分析2.利用共轭对称性,设计高效算法计算2个N点实序列的DFT。3.线性卷积及循环卷积的实现及二者关系分析4.比较DFT和FFT的运算时间5.利用FFT求信号频谱及分析采样…...

20240805软考架构--------每日打卡题21-25
每日打卡题21-25答案 21、【2014年真题】 难度:一般 在UML提供的系统视图中, (1) 是逻辑视图的一次执行实例,描述了并发与同步结构; (2) 是最基本的需求分析模型。 (1&a…...

GPT-5:未来已来,你准备好了吗?
GPT-5 一年半后发布?对此你有何期待? IT之家6月22日消息,在美国达特茅斯工程学院周四公布的采访中,OpenAI首席技术官米拉穆拉蒂被问及GPT-5是否会在明年发布,给出了肯定答案并表示将在一年半后发布。此外,穆…...

解决C#对Firebase数据序列化失败的难题
背景介绍 在当今的游戏开发领域,Unity与Firebase的结合日益普及。Firebase实时数据库提供了强大的数据存储和同步功能,使开发者能够轻松管理和使用数据。然而,在使用C#进行Firebase数据序列化和反序列化时,常常会遇到一些棘手的问…...

设计模式中的类关系
1. 依赖(Dependency) 定义:一个类使用到另一个类的实例,通常是通过方法参数、局部变量等。依赖关系是最弱的关系,因为它仅仅表示类之间的临时关联。 特征:在 UML 图中,依赖关系用带箭头的虚线…...

glibc的安装及MySQL的安全用户角色权限(twenty-one day)
一、glibc安装 mysql 清空/etc/目录下的my.cnf ls -l /etc/my.cnf rm -rf /etc/my.cnf yum -y remove mariadb find / -name "*mysql*" -exec rm -rf {} \; 安装mysql软件包 wget https://downloads.mysql.com/archives/get/p/23/file/mysql-8.0.33-li nux-glibc2.1…...

AttributeError: ‘ChatGLMTokenizer‘ object has no attribute ‘sp_tokenizer‘. 已解决
📑打牌 : da pai ge的个人主页 🌤️个人专栏 : da pai ge的博客专栏 ☁️宝剑锋从磨砺出,梅花香自苦寒来 ☁️运维工程师的职责:监…...

徐州BGP机房与普通机房的区别有哪些?
BGP也被称为是边界网关协议,是运行在TCP上的一种自治系统的路由协议,能够用来处理因特网大小的网络协议,同时也是能够处理好不相关路由域之间的多路连接的协议,今天小编主要来聊一聊徐州BGP机房与普通机房之间的区别有哪些&#x…...

VBA 程序运行中禁用鼠标键盘
1. Application.Interactive False:Excel 将阻止键盘和鼠标的所有输入,但代码显示的对话框的输入不受影响。 True:打开交互模式。 下面的代码程序一旦运行就会限定在Excel的事先选定的单元格输出。 如果注释掉Application.Interactive F…...
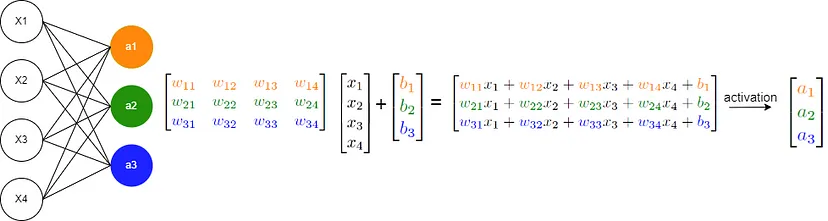
CUDA编程从零到壹
如今,当我们谈论深度学习时,为了提高性能,我们通常会将其实现与使用 GPU 联系起来。 GPU(图形处理单元)最初设计用于加速图像、2D 和 3D 图形的渲染。然而,由于它们能够执行许多并行操作,它们的…...

【国产开源可视化引擎】Meta2d.js API-Utils
Utils 常用功能函数 函数 formatPadding 将 padding 转换成数组格式 [top, right, bottom, left] padding 规则与 css padding 相同 参数: padding: Padding type Padding number | string | number[]; 返回: number[] 示例: formatP…...

大模型与数据分析的融合:创新与发展的新机遇
大模型与数据分析的融合:创新与发展的新机遇 前言大模型与数据分析的融合 前言 大模型与数据分析的融合正成为推动企业发展的关键力量。大模型在数据分析领域展现出了强大的能力。它能够以接近人类的水平理解和处理自然语言,快速、准确地解析大量非结构…...
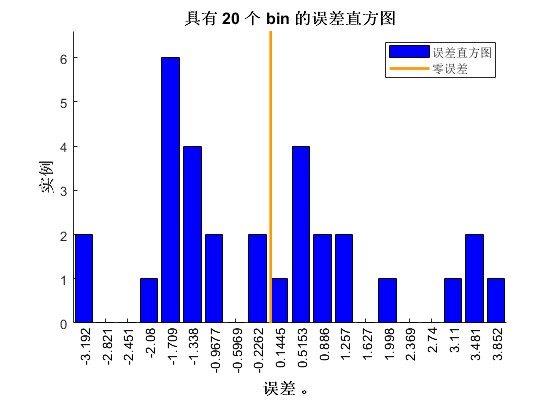
基于融合正余弦和柯西变异的麻雀搜索算法SCSSA优化CNN-BiLSTM的多变量时间序列预测
matlab R2024a以上 一、数据集 二、融合正余弦和柯西变异的麻雀搜索算法 麻雀搜索算法(Sparrow Search Algorithm, SSA)是一种新型的群体智能优化算法,其灵感来源于麻雀觅食行为。为了提高算法的性能,可以融合正余弦函数和柯西变…...

c++基本数据类型变量的最大值,最小值和内存空间
基本数据类型有哪些? 在C中,基本数据类型主要包括以下几种: 整型 (Integral Types): int:通常为32位,有 signed 和 unsigned 两种版本,如 int, unsigned int.short 或 signed short / unsigned …...

005集——运算符和循环——C#学习笔记
C# 提供了许多运算符。 其中许多都受到内置类型的支持,可用于对这些类型的值执行基本操作。 这些运算符包括以下组: 算术运算符,将对数值操作数执行算术运算比较运算符,将比较数值操作数布尔逻辑运算符,将对 bool 操作…...

【Tessent IJATG Users Manual】【Ch5】IJTAG Network Insertion
The IJTAG Network Insertion FlowIJTAG Network Insertion ExampleModification of the IJTAG Network Insertion Flow How to Edit or Modify a DftSpecificationEdit or Modify MethodDftSpecification Examples IJTAG Network Insertion 可以将已有的 instrument 连接起来&…...

我在高职教STM32——I2C通信入门(2)
大家好,我是老耿,高职青椒一枚,一直从事单片机、嵌入式、物联网等课程的教学。对于高职的学生层次,同行应该都懂的,老师在课堂上教学几乎是没什么成就感的。正是如此,才有了借助CSDN平台寻求认同感和成就感的想法。在这里,我准备陆续把自己花了很多心思设计的教学课件分…...

GPT解逻辑数学题之8个8变1000的故事
目录 初试正解 我: GPT4: 再问思索 我: GPT4: 提醒错误 我: GPT4: 给出正解提示 我: GPT4: 不愿放弃 我: GPT4: 再次尝试 我: …...

10、MySQL-索引
目录 1、索引概述 2、索引结构 2.1 BTree 2.2 BTree 2.3 Hash 3、索引分类 4、索引语法 4.1 创建索引 4.2 查看索引 4.3 删除索引 5、SQL性能分析 5.1 SQL执行频率 5.2 慢查询日志 5.3 profile详情 5.4 explain执行计划 6、索引使用 6.1 验证索引效率 6.2 最左…...

【python】Python操作Redis数据库的详细教程与应用实战
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 🏆 作者简介:景天科技苑 🏆《头衔》:大厂架构师,华为云开发者社区专家博主,…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...
