当前位置： 首页 > news >正文

SQL进阶技巧：有序数据合并问题之如何按照指定的规则对数据进行合并？【详解collect_list函数有序性保证】

news 2026/2/8 19:45:51

目录

0 问题描述【小红书面试题】

1 数据准备

2 问题分析

3 小结

0 问题描述【小红书】

有如下需求，需要将左边的表变换成右边的表，注意字段内容的顺序及对应内容的一致性。

第一个字段为name,第二个字段为subject，第三个字段为score，变换后要求subject按照语文、数学、英语排列，且score和subject之间内容保持一一对应。

1 数据准备

with data as (select '张三' as name , '数学' as subject , 80 as score  union allselect '张三' as name , '英语' as subject , 82 as score  union allselect '张三' as name , '语文' as subject , 95 as score  union allselect '李四' as name , '数学' as subject , 90 as score  union allselect '李四' as name , '英语' as subject , 93 as score  union allselect '李四

相关文章：

SQL进阶技巧：有序数据合并问题之如何按照指定的规则对数据进行合并？【详解collect_list函数有序性保证】

目录 0 问题描述【小红书面试题】 1 数据准备 2 问题分析 3 小结 0 问题描述【小红书】 有如下需求，需要将左边的表变换成右边的表，注意字段内容的顺序及对应内容的一致性。 第一个字段为name,第二个字段为subject，第三个字段为score，变换后要求subject按照语文、数学…...

编程日记 2024/8/9 19:52:09

windows和office微软官方免费激活教程

微软提供了windows系统和office的官方免费激活，其实不用去买什么激活码，官方提供了激活方式，完全免费。目前测试没发现什么问题，windows还支持永久激活，比一些乱七八糟的kms激活工具还省心。 github地址：Gi…...

编程日记 2024/8/9 19:49:04

【C++ 面试 - 基础题】每日 3 题（七）

✍个人博客：Pandaconda-CSDN博客 📣专栏地址：http://t.csdnimg.cn/fYaBd 📚专栏简介：在这个专栏中，我将会分享 C 面试中常见的面试题给大家~ ❤️如果有收获的话，欢迎点赞👍收藏&…...

编程日记 2024/8/9 19:48:03

Java面试题精选：消息队列(一)

1、为什么使用消息队列 问题用意： 其实就是想问一下消息队列有哪些使用场景，你项目中什么业务场景用到了消息队列，有什么技术挑战。使用MQ后给你带来了什么好处 规范回答： 消息队列的常见使用场景很多，但比较核心的…...

编程日记 2024/8/9 19:47:02

宝塔面板启用 QUIC 与 Brotli 的完整教程

环境 系统：Ubuntu 22.04.4 LTS x86_64 宝塔版本：7.7.0 (可使用本博客提供的一键安装优化脚本) nginx版本：1.26.1 开放UDP端口 注意：在你的服务器商家那里也要开放443 udp端口 sudo ufw allow 443/udp然后重新加载 UFW 以使新…...

编程日记 2024/8/9 19:46:00

Linux 进程调度（二）之进程的上下文切换

目录 一、概述二、上下文切换的实现1、context_switch2、switch_mm3、switch_to 三、观测进程上下文切换 一、概述 进程的上下文切换是指在多任务操作系统中，当操作系统决定要切换当前运行的进程时，将当前进程的状态保存起来，并恢复下一个要…...

编程日记 2024/8/9 19:44:58

Oracle事物临时表

在Oracle数据库中，事务临时表是一种特殊的表类型，主要用于存储在事务处理过程中产生的临时数据。这些表的数据只对当前会话或事务可见，并且在事务结束时会自动清除。 事务临时表的特点 生命周期： 事务临时表中的数据在事务提交或…...

编程日记 2024/8/9 19:40:53

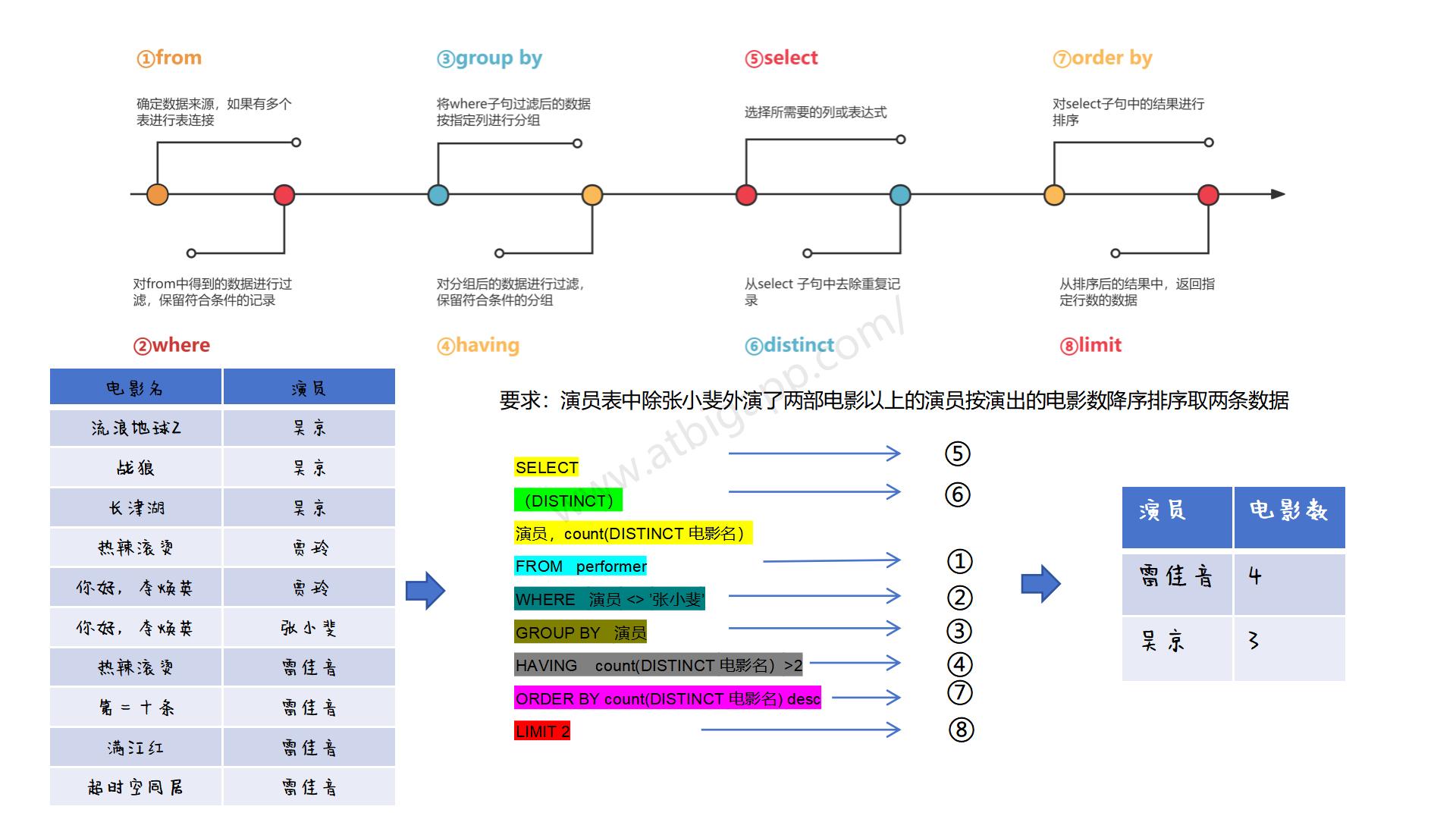
看图学sql之sql的执行顺序

学完前面的内容，我们已经掌握了基本的sql语法了，那我们学的 select, distinct, from, where,group by, having, order by, limit 他们具体的执行顺序是什么样的呢？ 语法： SELECT distinct column1, column2 FROM table1 join …...

编程日记 2024/8/9 19:39:52

百日筑基第四十五天-从JAVA8走到JAVA9

JAVA9新特性 Java 9发布于 2017 年 9 月 21 日 。 快速创建不可变集合 增加了List.of()、Set.of()、Map.of() 和 Map.ofEntries()等工厂方法来创建不可变集合（有点参考 Guava 的味道）： List.of("Java", "C"); Set.of…...

编程日记 2024/8/9 19:37:50

力扣第五十七题——插入区间

内容介绍 给你一个 无重叠的 ，按照区间起始端点排序的区间列表 intervals，其中 intervals[i] [starti, endi] 表示第 i 个区间的开始和结束，并且 intervals 按照 starti 升序排列。同样给定一个区间 newInterval [start, end] 表示另一个区…...

编程日记 2024/8/9 19:36:49

跟《经济学人》学英文：2024年08月03日这期 India’s economic policy will not make it rich

India’s economic policy will not make it rich A new World Bank report takes aim at emerging-market growth plans 原文： The developing world has fallen back in love with economic planning. As protectionism sweeps the West, poor countries are n…...

编程日记 2024/8/9 19:35:47

js 深拷贝、浅拷贝深度解析

赋值操作： let obj{a:1,b:[1,2,3],c:{m:2}}let newObjobjnewObj.a2newObj.b.push(4)newObj.c.m3console.log(obj,newObj); 将一个对象赋值给一个变量，其实就是将这个对象在栈内存中的引用地址复制给了这个变量，这两个对象指向堆内存中的同一个…...

编程日记 2024/8/9 19:33:44

CSS文本两端对齐

背景 如果我们要写了列表或表单类的样式&#xff0c;名称长短不一&#xff0c;但是想要两端对齐&#xff0c;如下面这样的&#xff1a; 你是怎么写的&#xff1f; 是这样的吗&#xff0c;在HTML里调整加空格&#xff1a; <ul><li>用户名</li><li>账 …...

编程日记 2024/8/9 19:31:42

C#中的foreach和自定义比较

在C#中foreach不能修改集合里面的值 在C#中&#xff0c;使用 foreach 循环遍历集合时&#xff0c;通常不建议修改集合中的元素&#xff0c;因为 foreach 循环是针对集合的枚举器进行操作的&#xff0c;而枚举器通常不支持修改集合中的元素。如果尝试在 foreach 循环中修改集合…...

编程日记 2024/8/9 19:30:41

有序转化数组（LeetCode）

题目 给你一个已经 排好序 的整数数组 和整数 、 、 。对于数组中的每一个元素 &#xff0c;计算函数值 &#xff0c;请 按升序返回数组 。 解题 在时间复杂度为解决问题 def sortTransformedArray(nums, a, b, c):def f(x):return a * x * x b * x cn len(nums)result…...

编程日记 2024/8/9 19:27:38

大数据信用报告查询有什么作用?怎么选择查询平台?

随着互联网的快速发展&#xff0c;人们的金融行为越来越多地依赖于网络平台。然而&#xff0c;网络上的金融交易存在着一定的风险&#xff0c;为了有效地防范这些风险&#xff0c;金融机构采用了大数据技术进行风险控制&#xff0c;下面&#xff0c;小易大数据平台将详细介绍大…...

编程日记 2024/8/9 19:24:35

import cv2ModuleNotFoundError: No module named ‘cv2‘

import cv2 ModuleNotFoundError: No module named cv2 (base) PS D:\CAMERA-D861T\LabelImg> pip3 install cv2 ERROR: Could not find a version that satisfies the requirement cv2 (from versions: none) ERROR: No matching distribution found for cv2 办法1 试了无…...

编程日记 2024/8/9 19:22:32

[Modbus] Modbus协议开发-基本概念（一）

历史 ModBus官网是Modicon&#xff08;Modicon早年已被施耐德收购&#xff09;公司为其PLC通讯而开发的一种通讯协议。 概述 通过Modbus协议&#xff0c;控制器之间、或控制器经由网络&#xff08;如以太网&#xff09;可以和其它设备之间进行通信。 优点 免费、好用、成熟…...

编程日记 2024/8/9 19:21:31

爬虫代理的使用：提升爬虫效率

爬虫代理的基本概念 爬虫代理&#xff0c;简单来说&#xff0c;就是位于客户端和目标服务器之间的一个中转站。当爬虫发起请求时&#xff0c;不是直接发送给目标服务器&#xff0c;而是先发送给代理服务器&#xff0c;再由代理服务器转发给目标服务器。目标服务器响应后&#…...

编程日记 2024/8/9 19:19:29

【gcc】基于gpt和python的流程和延迟梯度分析

Core Flow and Algorithm Concepts of GCC (Google Congestion Control) 【TWCC 】基于gpt和python简化分析webrtc拥塞控制论文: Analysis and Design of the Google Congestion Contro for Web Real-time Communication (WebRTC)参考大神的理解发送码率(send bitrate)影响了网…...

编程日记 2024/8/9 19:16:26

Ubuntu系统下交叉编译openssl

一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机&#xff1a;Ubuntu 20.04.6 LTSHost&#xff1a;ARM32位交叉编译器&#xff1a;arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

编程新知 2025/11/10 15:33:04

智慧医疗能源事业线深度画像分析（上）

引言 医疗行业作为现代社会的关键基础设施，其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入，智慧医疗能源事业线应运而生，致力于通过创新技术与管理方案，重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

编程新知 2026/2/5 4:39:34

AI Agent与Agentic AI：原理、应用、挑战与未来展望

文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例&#xff1a;使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例&#xff1a;使用OpenAI GPT-3进…...

编程新知 2026/1/23 7:04:53

从深圳崛起的“机器之眼”：赴港乐动机器人的万亿赛道赶考路

进入2025年以来&#xff0c;尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断&#xff0c;但全球市场热度依然高涨&#xff0c;入局者持续增加。 以国内市场为例&#xff0c;天眼查专业版数据显示&#xff0c;截至5月底&#xff0c;我国现存在业、存续状态的机器人相关企…...

编程新知 2026/2/8 7:23:45

OkHttp 中实现断点续传 demo

在 OkHttp 中实现断点续传主要通过以下步骤完成&#xff0c;核心是利用 HTTP 协议的 Range 请求头指定下载范围&#xff1a; 实现原理 Range 请求头&#xff1a;向服务器请求文件的特定字节范围&#xff08;如 Range: bytes1024-&#xff09; 本地文件记录&#xff1a;保存已…...

编程新知 2025/12/12 0:56:22

HDFS分布式存储 zookeeper

hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架&#xff0c;允许使用简单的变成模型跨计算机对大型集群进行分布式处理&#xff08;1.海量的数据存储 2.海量数据的计算&#xff09;Hadoop核心组件 hdfs&#xff08;分布式文件存储系统&#xff09;&a…...

编程新知 2026/1/24 4:10:44

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)

漏洞概览 漏洞名称&#xff1a;Apache Flink REST API 任意文件读取漏洞CVE编号&#xff1a;CVE-2020-17519CVSS评分&#xff1a;7.5影响版本&#xff1a;Apache Flink 1.11.0、1.11.1、1.11.2修复版本&#xff1a;≥ 1.11.3 或 ≥ 1.12.0漏洞类型&#xff1a;路径遍历&#x…...

编程新知 2026/2/6 2:13:58

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战

说明&#xff1a;这是一个机器学习实战项目&#xff08;附带数据代码文档&#xff09;&#xff0c;如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下&#xff0c;风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

编程新知 2026/1/25 4:19:49

MySQL 8.0 事务全面讲解

以下是一个结合两次回答的 MySQL 8.0 事务全面讲解&#xff0c;涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容&#xff0c;并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念&#xff08;ACID&#xff09; 事务是…...

编程新知 2025/9/19 22:12:36

NPOI Excel用OLE对象的形式插入文件附件以及插入图片

static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

编程新知 2025/10/6 2:06:51