密码学中的承诺
Commitment
概述
密码学承诺是一个涉及两方的二阶段交互协议,双方分别为承诺方和接收方。简述来说,它的功能涵盖不可更改性和确定性。
承诺方发送的消息密文,一旦发出就意味着不会再更改,而接收方收到这个消息可以进行验证结果。
特点就是无需第三方就可以进行验证。
举个例子:猜拳问题
假设有人在猜拳中老是不按时出拳,那么在看到对方的结果再出拳,显然是不公平的,在没有第三方的情况下,怎样保证无人作弊呢?那就是承诺。
这里使用一个哈希函数构造一个简单的承诺方案,双方选取一个足够安全的哈希函数H(x)H(x)H(x),将猜拳的三种出拳方法定为一组数字如x1,x2,x3x_1,x_2,x_3x1,x2,x3。那么方案如下,
- 选手一选择一个出拳方法xix_ixi(如x1x_1x1),再选取一个随机数rir_iri如(r1r_1r1),计算承诺H(x1∣∣r1)H(x_1||r_1)H(x1∣∣r1),并把它发送给选手二。
- 选手二也选择一个出拳方法(如x3x_3x3),同样也选择一个随机数r2r_2r2,计算承诺H(x2∣∣r2)H(x_2||r_2)H(x2∣∣r2),并把它发送给选手一。
- 双方都收到承诺后,都公布自己的xix_ixi和rir_iri,然后进行验证即可
选择添加随机数的原因主要预防某一方直接算出三种出拳方式的哈希,然后接收到了另一方的哈希后,直接进行对比作弊。
可以看到承诺主要分为两个阶段
- Commit Phase:把暂时不想公开的消息(即前面的出拳方案)再加一个随机数,加密后(如前面的计算哈希)发送给对方;
- Reveal Phase:公开秘密和随机数。
性质
承诺具有两个基本性质:隐藏性(Hiding)和绑定性(Binding),隐藏也就是承诺值是不会泄漏有关原消息的任何信息的,而绑定就是接收方可以确信收到的消息是该承诺对应的消息,不可能再找到一个不同的消息从而诞生同一个承诺。
而衡量性质强度一般有两个标准 Perfectly和Computationally,前者代表即便有无穷计算能力也不能破坏掉该性质,后者则是以目前的计算能力在可忍受的时间里是不能破坏该性质的。
但不存在Perfectly Hiding和Perfectly Binding,假设存在一个Perfectly Hiding,那么为了不泄露原消息,一定会有多个消息能计算出同一个承诺,这恰好违背了Binding的性质。
常用方案
主要是拥有Perfectly hiding and computationally binding的Pedersen Commitment 和 拥有Perfectly binding but computationally hiding的 ElGamal Commitment
Pedersen Commitment
DL(离散对数)
选择一个阶为qqq的乘法群GGG,再选择两个元素g,h∈Gqg,h \in G_qg,h∈Gq,xxx是消息,rrr是随机数
- Commit Phase:Commit(x,r)=gxhrCommit(x,r)=g^xh^rCommit(x,r)=gxhr
- Reveal Phase:公开x,rx,rx,r
加同态
Commit(x1,r1)×Commit(x2,r2)=gx1hr1×gx2hr2=gx1+x2hr1+r2=Commit(x1+x2,r1+r2)\begin{aligned} Commit(x_1,r_1) \times Commit(x_2,r_2) &= g^{x_1}h^{r_1} \times g^{x_2}h^{r_2}\\ &=g^{x_1+x_2}h^{r_1+r_2} \\ &=Commit(x_1+x_2,r_1+r_2) \end{aligned}Commit(x1,r1)×Commit(x2,r2)=gx1hr1×gx2hr2=gx1+x2hr1+r2=Commit(x1+x2,r1+r2)
ECC(椭圆曲线)
选择椭圆曲线上的一个基点GGG和随机一个点HHH
- Commit Phase:Commit(x,r)=Gx+HrCommit(x,r)=Gx+HrCommit(x,r)=Gx+Hr
- Reveal Phase:公开x,rx,rx,r
加同态
$\begin{aligned}
\end{aligned}$Commit(x1,r1)+Commit(x2,r2)=Gx1+Hr1+Gx2+Hr2=(x1+x2)G+(r1+r2)H=Commit(x1+x2,r1+r2)\begin{aligned} Commit(x_1,r_1) + Commit(x_2,r_2) &= Gx_1+Hr_1 + Gx_2+Hr_2 \\ &=(x_1+x_2)G+(r_1+r_2)H \\ &=Commit(x_1+x_2,r_1+r_2) \end{aligned}Commit(x1,r1)+Commit(x2,r2)=Gx1+Hr1+Gx2+Hr2=(x1+x2)G+(r1+r2)H=Commit(x1+x2,r1+r2)
ElGamal Commitment
假设GGG是阶为qqq的循环群,而g,hg,hg,h是GGG的两个随机生成元。消息m∈Gm \in Gm∈G,随机数r∈Zqr \in \mathbb{Z}_qr∈Zq
- Commit Phase:Commit=(gr,mhr)Commit=(g^r,mh^r)Commit=(gr,mhr)
- Reveal Phase:公开(m,r)(m,r)(m,r)
参考
密码学承诺之Pedersen commitment原理及应用
Commitment Scheme
Pedersen, T. P. (1991). Non-Interactive and Information-Theoretic Secure Verifiable Secret Sharing. Advances in Cryptology - CRYPTO '91, 129-140. doi: 10.1007/3-540-46766-1_9
相关文章:

密码学中的承诺
Commitment 概述 密码学承诺是一个涉及两方的二阶段交互协议,双方分别为承诺方和接收方。简述来说,它的功能涵盖不可更改性和确定性。 承诺方发送的消息密文,一旦发出就意味着不会再更改,而接收方收到这个消息可以进行验证结果。…...
)
redis入门实战一、五种数据结构的基本操作(二)
redis入门实战一、五种数据结构的基本操作【二】 一、String1)、set2)、getset3)、msetnx 给多个元素赋值,原子操作4)、字符串 追加 & 取部分数据5)、数值可以做加减,指定增量大小6)、获取长度7)、 bitmap①、setbit②、bitop 二进制与或运算(效率高)③、bitcou…...

day13 模块和异常捕获总结
day13 模块和异常捕获 一、生成器 (一)、什么是生成器 1)容器(是一种可以创建多个数据的容器),生成器中保存的是创建数据的方法,而不是数据本身。2)特点: a. 打印生成…...
【Linux】进程优先级 环境变量
进程优先级 环境变量 一、进程优先级1、基本概念2、查看以及修改系统进程的优先级3、一些其他的关于进程优先级的指令和函数调用4、与进程优先级有关的一些进程性质二、环境变量1、基本概念2、和环境变量相关的命令3、Linux中的常见环境变量介绍4、环境变量的组织方式以及在C代…...

UE实现建筑分层抽屉展示效果
文章目录 1.实现目标2.实现过程2.1 基础设置2.2 核心函数3.参考资料1.实现目标 使用时间轴对建筑楼层的位置偏移进行控制,实现分层抽屉的动画展示效果。 2.实现过程 建筑抽屉的实现原理比较简单,即对Actor的位置进行偏移,计算并更新其世界位置即可。这里还是基于ArchVizExp…...

【C语言进阶:刨根究底字符串函数】 strstr 函数
本节重点内容: 深入理解strstr函数的使用学会strstr函数的模拟实现⚡strstr strstr的基本使用: #define _CRT_SECURE_NO_WARNINGS #include <stdio.h> #include<string.h>int main() {char arr1[] "abcdebcdef";char arr2[] &…...
SpringBoot实战(十二)集成Actuator
目录一、简介二、Maven依赖三、使用入门1.HTTP 方式访问端点2.JMX 方式访问端点3.端点信息整理4.端点的启用与禁用5.端点的公开6.保护 HTTP 端点7.配置 CORS 跨域官方文档: https://docs.spring.io/spring-boot/docs/2.4.5/reference/htmlsingle/#production-ready …...

学习系统编程No.7【进程替换】
引言: 北京时间:2023/3/21/7:17,这篇博客本来昨天晚上就能开始写的,但是由于笔试强训的原因,导致时间用在了做题上,通过快2个小时的垂死挣扎,我充分意识到了自己做题能力的缺陷和运用新知识的缺…...
、Java并发)
【3.22】操作系统内存管理(整理)、Java并发
3. 内存管理 为什么要有虚拟内存? 我们想要同时在内存中运行多个程序,就需要把进程所使用的地址隔离,所以使用了虚拟内存。简单来说,虚拟内存地址是程序使用的内存地址。物理内存地址是实际存在硬件里面的地址。 操作系统为每个…...

电脑文件丢失怎么找回来
电脑文件丢失怎么找回来?最近打开电脑时,它启动得很慢。刚刚开始我没有没在意,就重启了当我再次打开电脑时,发现桌面上的文件消失了,面对这种意外情况,有什么办法可以快速找到呢? 电脑文件丢失后,想要找回…...
Python(白银时代)——面向对象
基本概念 面向过程 是早期的一个编程概念,类似函数,但是没有返回值 具体做法: 把完成某个需求的所有步骤,从头到尾 逐步实现 将某些功能独立的代码 封装成一个又一个 函数 然后顺序调用不同的函数 特点: 注重 步骤…...

Python流星雨代码
前言 用Python画场流星雨看看,源码见文末公众号哈。 流星类 def __init__(self): self.r ra.randint(50,100) self.t ra.randint(1,3) self.x ra.randint(-2000,1000) #流星的横坐标 self.y ra.randint(0,500) #流星…...
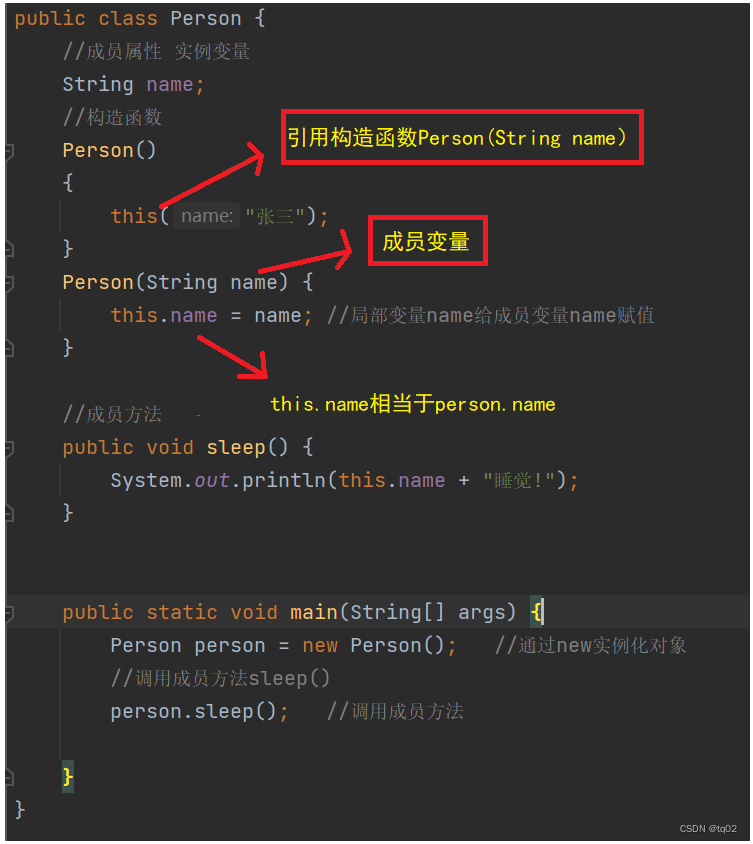
Java语言-----类与对象的秘密
目录 前言 一、类与对象的介绍 二、类的实例化 三.类与对象的使用方法 3.1对象的初始化 3.2内存显示图 四.this的使用方法 总结 😽个人主页: tq02的博客_CSDN博客-C语言,Java领域博主 🌈理想目标:努力学习,向Java进…...
大数据处理学习笔记2.1 初识Spark
文章目录零、本节学习目标一、Spark的概述(一)Spark的组件1、Spark Core2、Spark SQL3、Spark Streaming4、MLlib5、Graph X6、独立调度器、Yarn、Mesos(二)Spark的发展史1、发展简史2、目前最新版本二、Spark的特点(一…...

太强了,英伟达面对ChatGPT还有这一招...
大家好,我是 Jack。 今年可谓是 AI 元年,ChatGPT、AIGC、VITS 都火了一波。 我也先后发布了这几期视频: 这是一个大模型的时代,AI 能在文本、图像、音频等领域大放异彩,得益于大模型。而想要预训练大模型,…...

【微服务】—— Nacos注册中心
文章目录一、Nacos 注册中心的设计原理1、数据模型2、数据⼀致性3、负载均衡4、健康检查二、Nacos 注册中心服务数据模型1、服务(Service)和服务实例(Instance)1)定义服务2)服务元数据3)定义实例…...

GPT-4是个编程高手,真服了!
上周给大家发了一个GPT-4教数学的介绍,很多人都被震撼了,感觉有可能在教育行业引发革命。它在编程领域表现如何?先不说能否替代程序员,这个还有待更多的测试和反馈,我想先试试它能不能像教数学那样教编程。我找了个Jav…...
基于深度学习的车型识别系统(Python+清新界面+数据集)
摘要:基于深度学习的车型识别系统用于识别不同类型的车辆,应用YOLO V5算法根据不同尺寸大小区分和检测车辆,并统计各类型数量以辅助智能交通管理。本文详细介绍车型识别系统,在介绍算法原理的同时,给出Python的实现代码…...
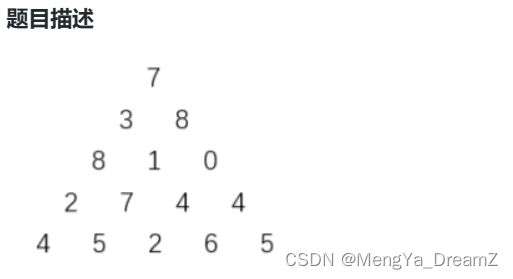
【蓝桥杯C++】3月21日刷题集训ABC-附百分代码,一目了然
目录 刷题集训 A Day 1 成绩分析 Day 1 饮料换购 刷题集训 B Day 1 分巧克力 Day 1 递增三元组 Day 1 小明的衣服 刷题集训 C Day 1 数字三角形 Day 1 跳跃 Day 1 蓝太子序列 刷题集训 A Day 1 成绩分析 题目描述 小蓝给学生…...
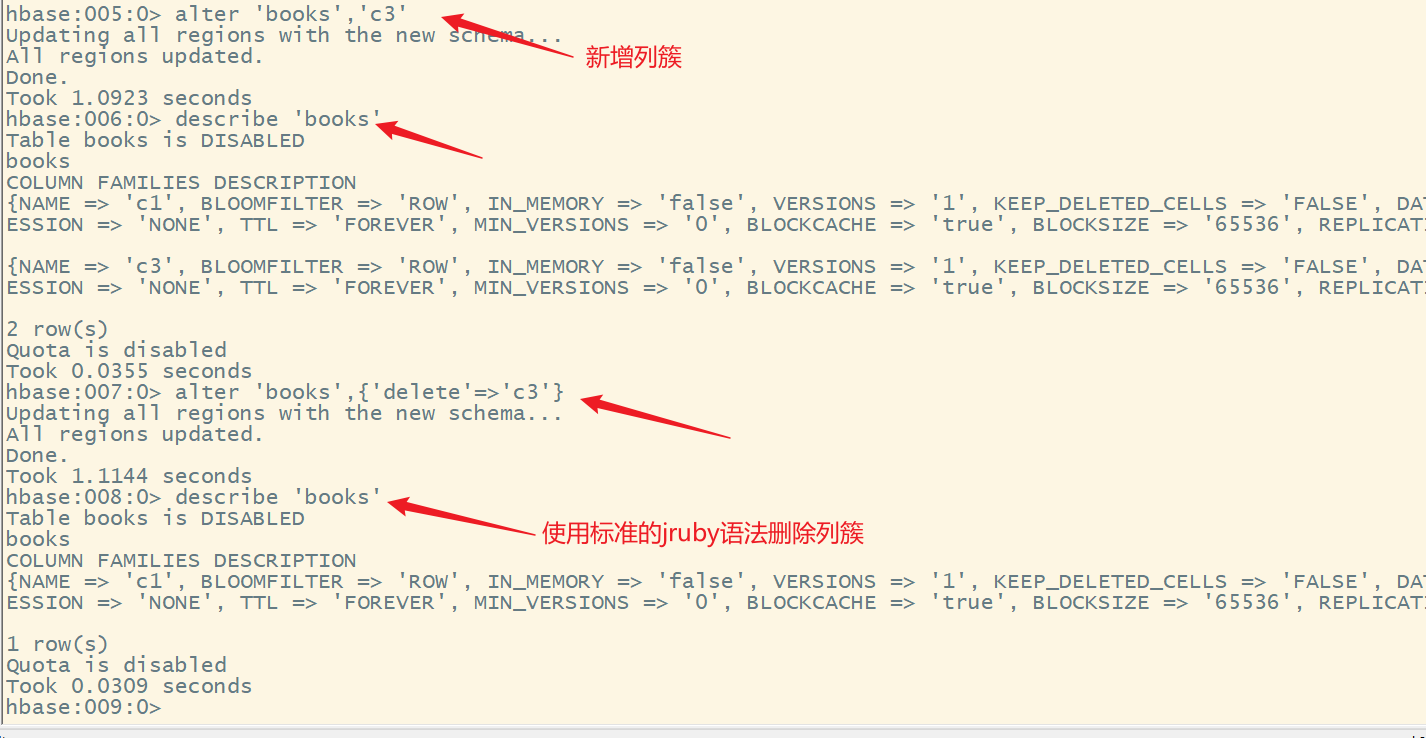
HBase高手之路4-Shell操作
文章目录HBase高手之路3—HBase的shell操作一、hbase的shell命令汇总二、需求三、表的操作1.进入shell命令行2.创建表3.查看表的定义4.列出所有的表5.删除表1)禁用表2)启用表3)删除表四、数据的操作1.添加数…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...
