最优化算法 - 动态规划算法
动态规划算法简介
动态规划(Dynamic programming)是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。 动态规划常常适用于有重叠子问题和最优子结构性质的问题,动态规划方法所耗时间往往远少于朴素解法。
动态规划算法是一种常用的优化算法,用于解决一些具有重叠子问题和最优子结构的问题,例如背包问题、最长公共子序列、矩阵连乘等。动态规划算法通过将问题划分为若干个重叠的子问题,并保存子问题的解,以避免重复计算,从而提高算法效率。
动态规划算法的基本思想是将一个大问题分解成若干个小问题,求解每个小问题的最优解,并保存下来。通过组合每个小问题的最优解,得到大问题的最优解。动态规划算法通常使用递归或迭代的方式实现。
动态规划算法是一种非常有用的算法设计技术,它适用于许多实际问题的求解。在实际应用中,我们需要根据问题的特点选择合适的动态规划算法,并注意避免时间和空间复杂度的过度增长。
动态规划算法步骤
-
定义问题的状态:通常使用一个或多个变量来表示问题的状态,例如背包问题中的剩余容量、最长公共子序列问题中的两个字符串的索引等。
-
定义状态转移方程:根据子问题之间的关系,定义状态转移方程。这个方程通常是一个递推式,用于计算当前状态的最优解。
-
初始化:将初始状态的最优解保存下来,通常是一个边界条件。
-
递推求解:使用状态转移方程求解每个子问题的最优解,并保存下来。
-
求解大问题:根据子问题的最优解,组合得到大问题的最优解。
动态规划算法应用
- 背包问题:将一些物品放入容量有限的背包中,使得所放物品总价值最大。
- 最长公共子序列问题:找到两个字符串中最长的相同子序列。
- 计算编辑距离:将一个字符串转换为另一个字符串所需的最少操作数。
- 矩阵链乘问题:将一堆矩阵相乘,找到最小的计算次数。
- 找零钱问题:找到最少的硬币数,以凑出给定的金额。
- 最大子序和问题:找到一个序列中连续的子序列,使得子序列的和最大。
动态规划算法示例
背包算法(Knapsack algorithm)是一种动态规划算法,用于在给定的一组物品中,选择一些物品装入背包,使得装入的物品总重量不超过背包容量,同时总价值最大。该问题被称为背包问题(Knapsack problem)。
背包问题有两种形式:01背包和完全背包。01背包问题中,每个物品最多只能选择一次,而在完全背包问题中,每个物品可以选择任意多次。
算法思路:
- 创建一个二维数组dp,其中dp[i][j]表示前i个物品放入容量为j的背包中所能获得的最大价值。
- 初始化dp数组的第一行和第一列为0,因为当背包容量为0或没有物品可选时,最大价值都为0。
- 遍历物品列表,并在dp数组中填充每个物品的最大价值。对于第i个物品,如果它的重量小于等于当前背包容量j,则可以选择放入背包或不放入背包。如果选择放入,那么背包内的可选物品为前i-1个物品,背包容量为j-w[i],价值为dp[i-1][j-w[i]] + v[i]。如果选择不放入,那么背包内的可选物品为前i-1个物品,背包容量为j,价值为dp[i-1][j]。选取两者中的最大值作为dp[i][j]的值。
- 最终,dp[n][m]即为所求的最大价值。
实现代码(Java):
public static int knapsack(int[] weight, int[] value, int W) {int n = weight.length;int[][] dp = new int[n + 1][W + 1];for (int i = 0; i <= n; i++) {for (int j = 0; j <= W; j++) {if (i == 0 || j == 0) {dp[i][j] = 0;} else if (weight[i - 1] <= j) {dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]] + value[i - 1]);} else {dp[i][j] = dp[i - 1][j];}}}return dp[n][W];
}
其中,weight是物品的重量数组,value是物品的价值数组,W是背包的容量。
动态规划算法对比
动态规划算法和分治算法都是常用的算法设计技术,但它们之间有一些区别。
相同点:动态规划算法和分治算法都是将一个大问题分解成若干个小问题,然后求解每个小问题的解,最后将所有小问题的解组合起来得到大问题的解。
不同点:动态规划算法和分治算法的主要区别在于它们对子问题的处理方式。
(1)动态规划算法将子问题的解保存下来,以避免重复计算。在求解一个问题时,动态规划算法通常需要先求解其子问题,然后将子问题的解保存起来,最后利用子问题的解求解大问题。动态规划算法通常适用于具有重叠子问题和最优子结构的问题。
动态规划算法通常适用于求解最优化问题,例如背包问题、最长公共子序列问题、矩阵连乘问题等。
(2)分治算法则是将子问题分解成独立的部分,然后对每个部分分别求解,最后将各个部分的解组合起来得到大问题的解。分治算法通常适用于具有相互独立的子问题的问题。
分治算法通常适用于分布式计算、排序和查找等问题,例如归并排序、快速排序、二分查找等。
相关文章:

最优化算法 - 动态规划算法
动态规划算法简介 动态规划(Dynamic programming)是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。 动态规划常常适用于有重叠子问题和最优子结构性质的问题…...
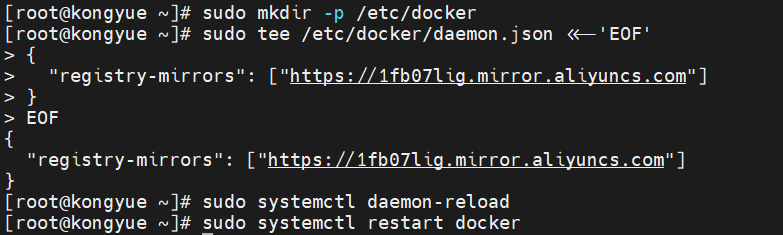
springCloud学习【3】之Docker(1)
文章目录一 Docker环境准备1.1 应用部署的环境问题1.2 Docker简介1.3 Docker解决操作系统环境差异1.4 Docker和虚拟机的区别1.5 Docker架构1.5.1 镜像和容器1.5.2 DockerHub1.5.3 Docker架构1.5.4 Docker工作流1.6 Docker的安装和启动1.7 安装步骤1.8 启动Docker1.9 配置镜像加…...
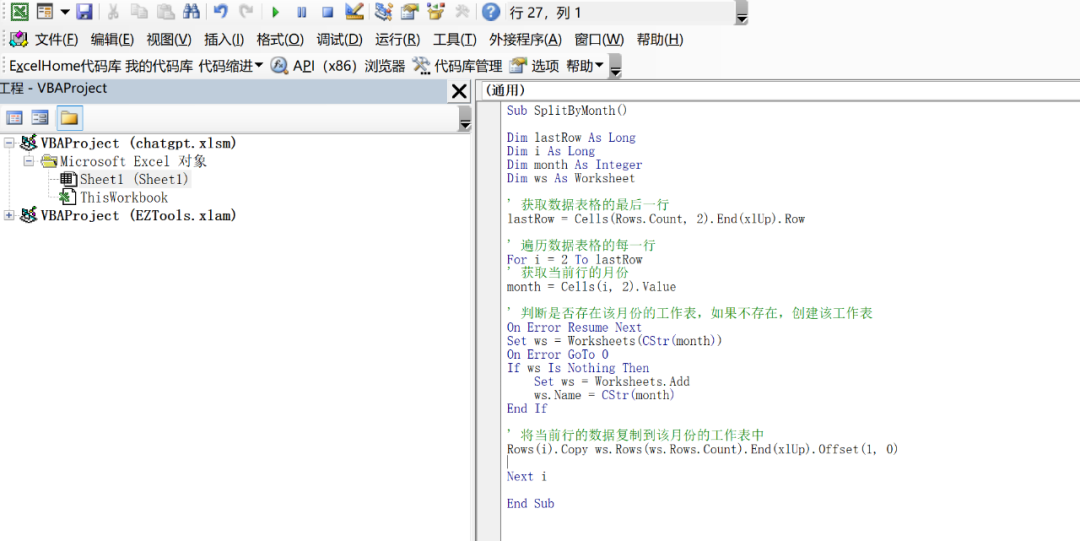
难以置信,已经有人用 ChatGPT 做 Excel 报表了?
要问2023年初科技领域什么最火,那自然是 ChatGPT。 ChatGPT 由人工智能研究实验室 OpenAI 于2022年11月30日推出。上线短短5天,用户数量已突破100万,在今年2月份,用户数量已经突破1亿。 ChatGPT 是一个超级智能聊天机器人&#…...
、HAL_NVIC_EnableIRQ())
中断相关操作函数HAL_NVIC_SetPriority()、HAL_NVIC_EnableIRQ()
文章目录HAL_NVIC_SetPriority():设置中断优先级HAL_NVIC_EnableIRQ():使能中断结束HAL_NVIC_SetPriority():设置中断优先级 HAL_NVIC_SetPriority()函数是一个用于设置中断优先级的函数,其定义如下: void HAL_NVIC_…...
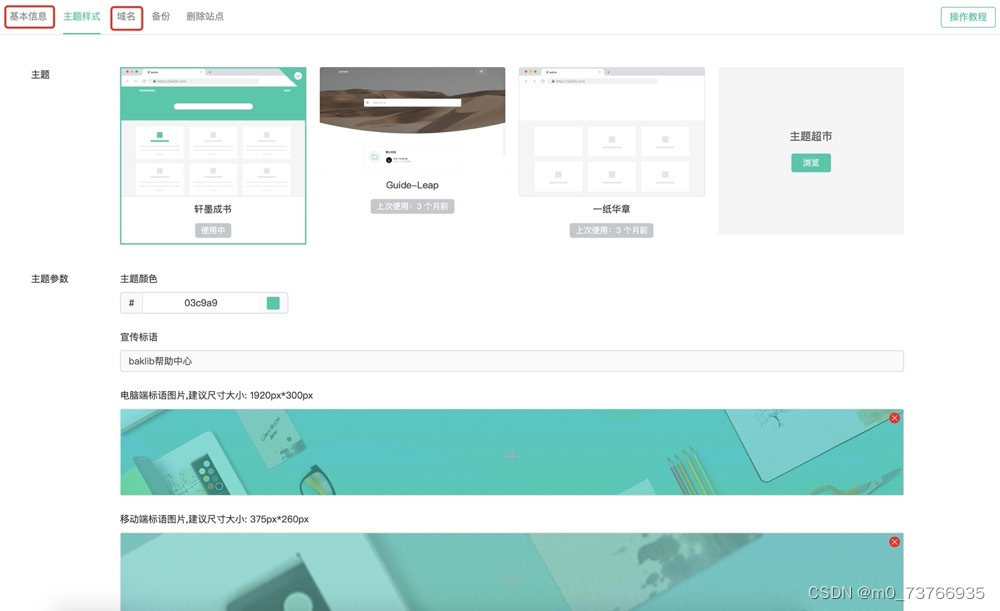
企业增长秘诀丨设立优质的帮助中心,加深用户产品使用深度,促进产品转化
客户的留存问题一直备受企业关注,留存率的高低反应了产品的真实状况,将直接影响企业后期的发展规划。下文将为大家剖析下产品中客户的转化流程,以及如何提高产品的使用深处与复购率。 产品中,从客户生命周期角度,可分…...
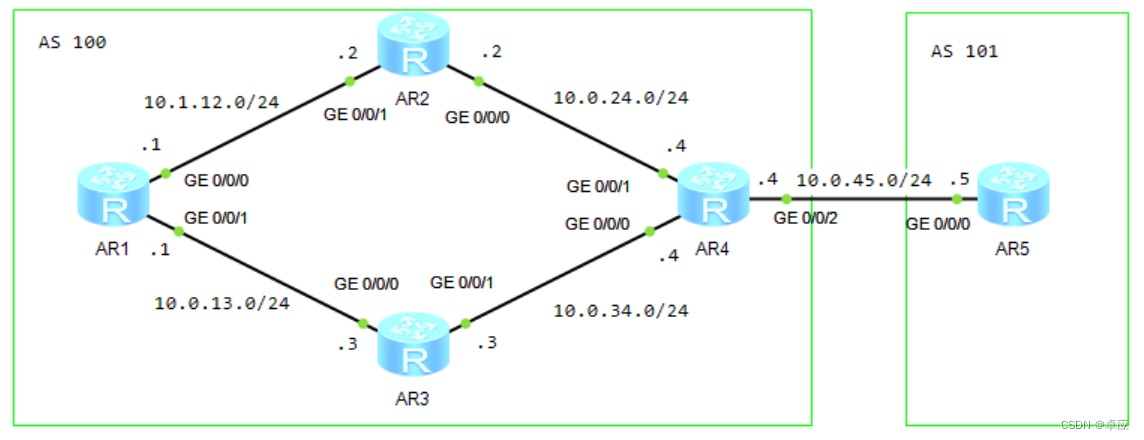
3.OSPF与BGP的联动
14.3实验3:OSPF与BGP联动配置 实验目的实验拓扑实验步骤 配置IP地址 AR1的配置 <Huawei>system-view Enter system view, return user view with CtrlZ. [Huawei]undo info-center enable Info: Information center is disabled. [Huawei]sysname AR1 …...
机器学习算法——决策树详解
文章目录前言:决策树的定义熵和信息熵的相关概念信息熵的简单理解经典的决策树算法ID3算法划分选择或划分标准——信息增益ID3算法的优缺点C4.5算法信息增益率划分选择或划分标准——Gini系数(CART算法)Gini系数计算举例CART算法的优缺点其他…...

配置Jenkins
目录 一.前言 1.1简介 1.2工作步骤图 二.配置jenkins部署项目 2.1项目新建 2.2jenkinsfile文件如下 三.jenkins工作台配置 3.1.点击新建item进入新建页面,输入任务名称,选择pipeline 3.2.选择第二个配置 3.4将ideal中jenkinsfile文件的路径粘入脚本路径中 3.5启动项目…...
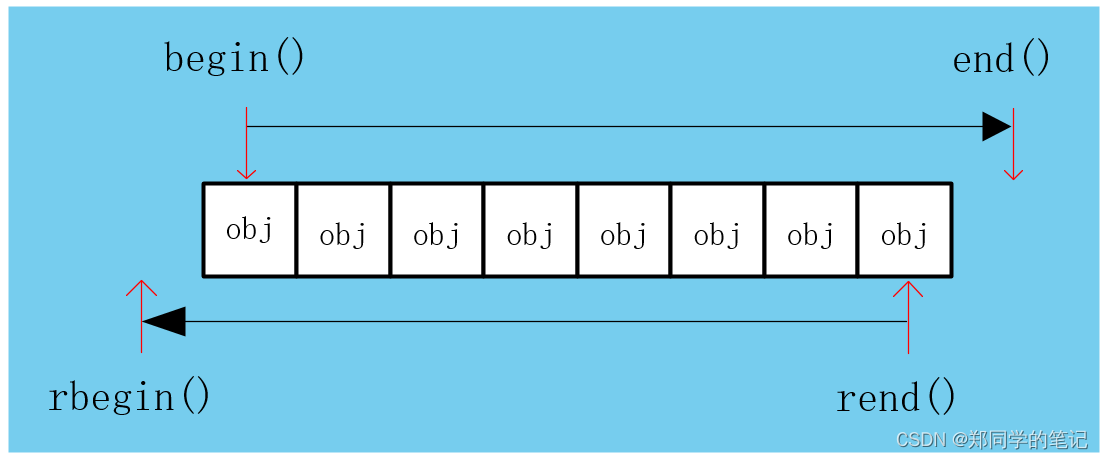
【STL三】序列容器——array容器
【STL三】序列容器——array一、array简介二、头文件三、模板类四、成员函数1、迭代器2、元素访问3、容量4、操作五、demo1、容量(不使用迭代器)2、使用迭代器3、元素访问 at()、front()、back()、data()一、array简介 array 容器是 C 11 标准中新增的序…...
【STL四】序列容器——vector容器
【STL容器】序列容器——vector容器一、简介二、头文件三、模板类四、成员函数1、迭代器2、元素访问3、容量4、修改操作五、demo1、容量reserve、capacity、shrink_to_fit2、修改操作pop_back()、push_back3、修改操作insert()4、修改操作emplace()5、修改操作erase()、swap()、…...
4年功能测试,我一进阶python接口自动化测试,跳槽拿了20k......
目录:导读前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜)前言 很多人在这求职市场…...
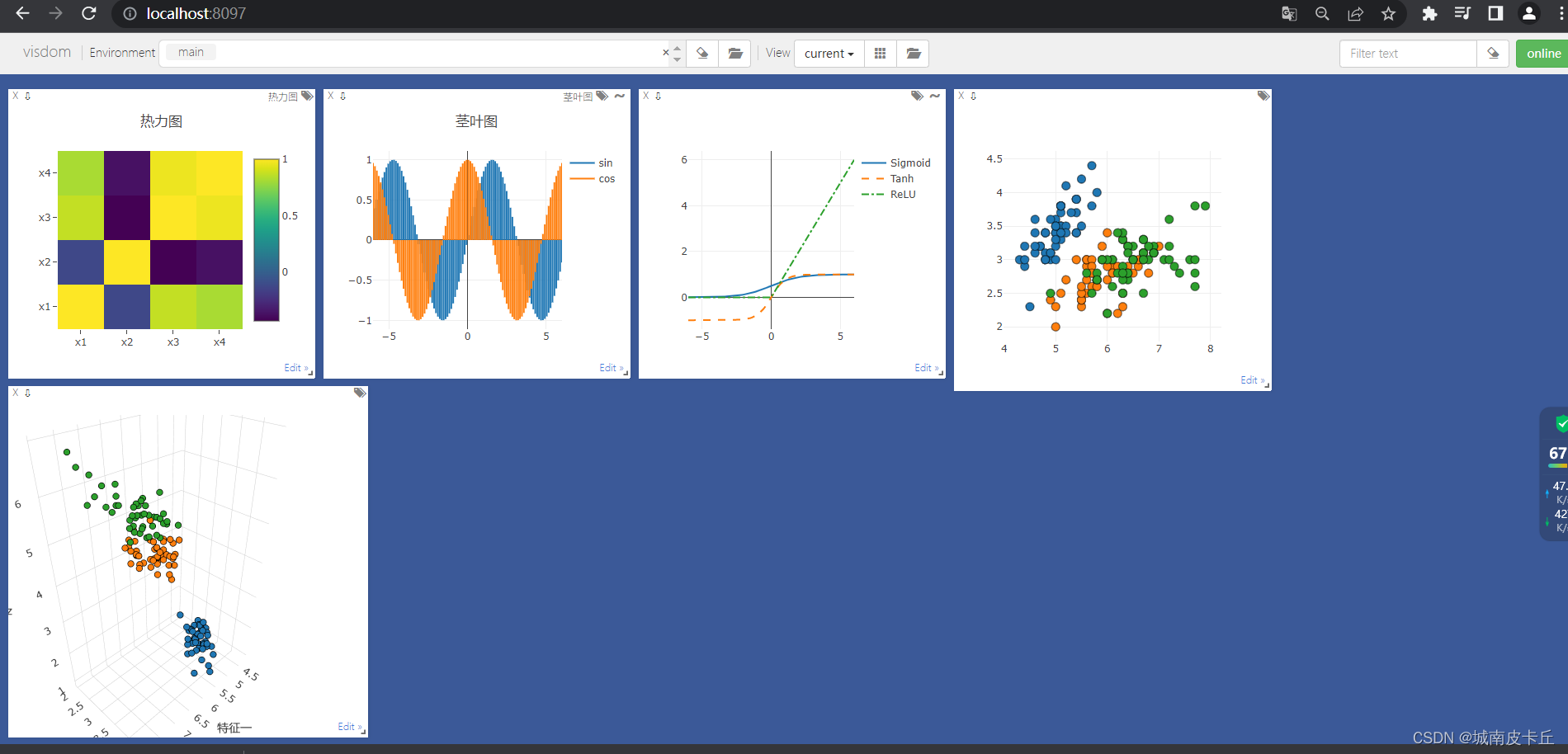
基于Pytorch的可视化工具
深度学习网络通常具有很深的层次结构,而且层与层之间通常会有并联、串联等连接方式。当使用PyTorch建立一个深度学习网络并输出文本向读者展示网络的连接方式是非常低效的,所以需要有效的工具将建立的深度学习网络结构有层次化的展示,这就需要…...
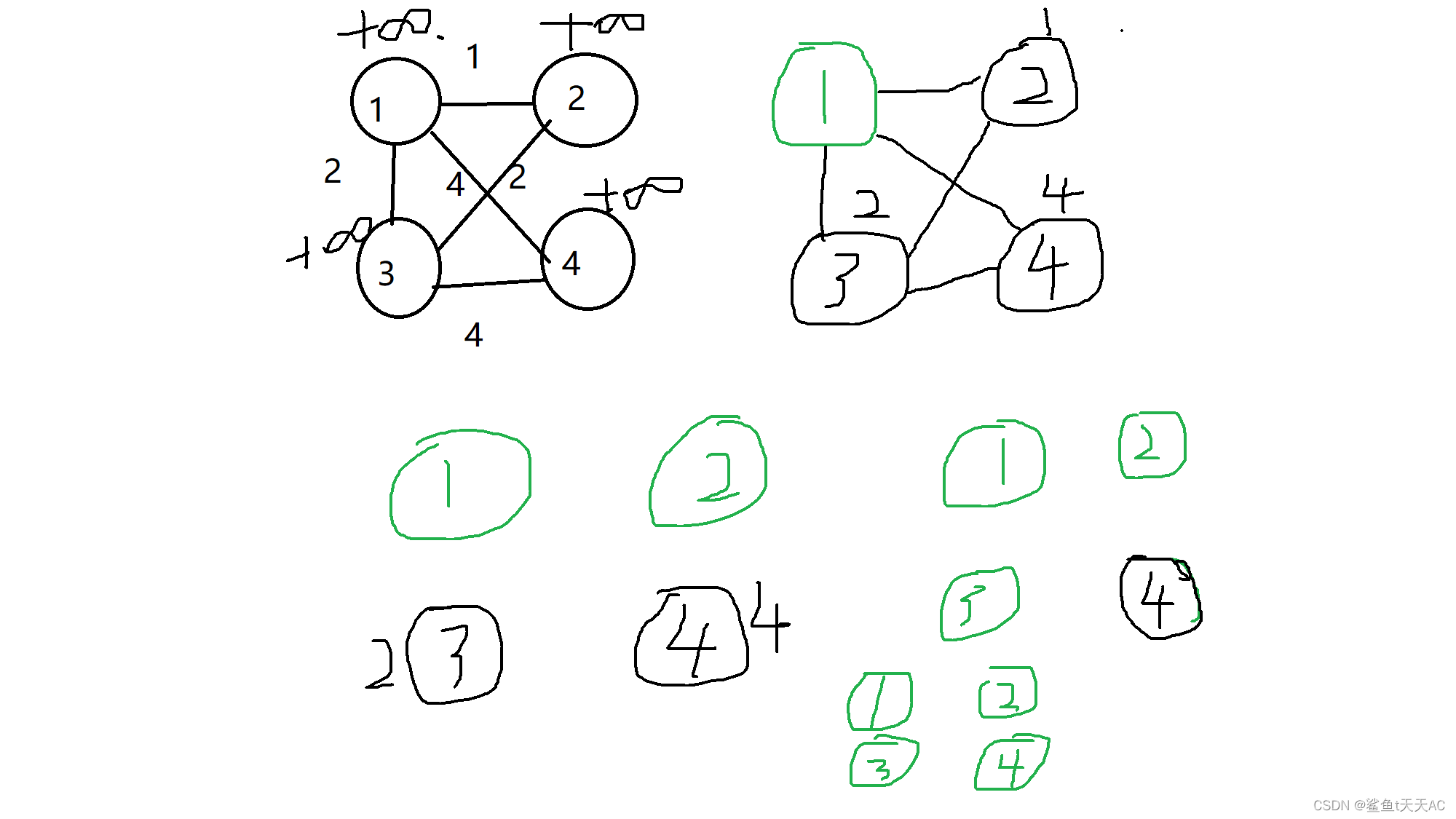
XCPC第十一站,带你学会图论基本算法
我们约定:以下n表示点的数目,m表示边的数目。 引子1——邻接表存储图的方法()(暂时不考虑重边和自环) 现在我们有n个点(编号为1~n)和m条边,要用数组存储它们,…...
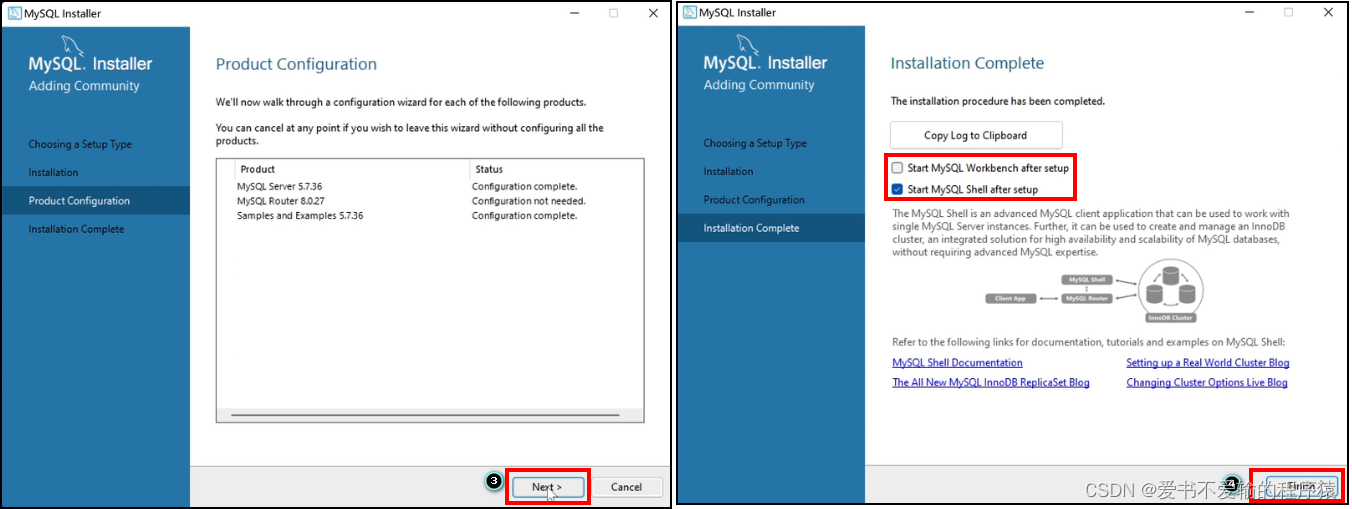
【MySQL】1 MySQL的下载、安装与配置|提供安装包
欢迎来到爱书不爱输的程序猿的博客, 本博客致力于知识分享,与更多的人进行学习交流 目前,已开了以下专栏,欢迎关注与指导 1️⃣Java基础知识系统学习(持续更文中…) 2️⃣UML(已更完) 3️⃣MySQL(持续更文中…) MYSQL的下载、安装与配置1.下载MySQL5.71.1安装包的获…...

Redis 事务
目录Redis 事务一、Redis事务的概念:二、redis事务提出的逻辑:三、redis事务的基本操作四、事务的执行流程五、redis锁六、redis分布式锁Redis 事务 一、Redis事务的概念: Redis 事务的本质是一组命令的集合。事务支持一次执行多个命令&…...

【linux】:进程控制
文章目录 前言一、什么是写时拷贝二、进程控制 1.进程终止2.进程等待三丶进程程序替换总结前言 了解上一篇文章中的进程地址空间后,我们再来说说进程控制的概念,进程控制我们需要搞清楚三个问题:如何进程终止,如何解决僵尸进程问…...
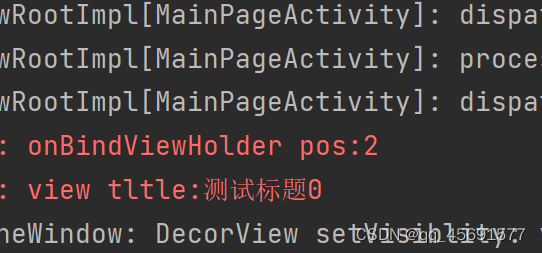
在recyclerview中使用其item布局的ViewBinding类需要注意的问题
问题描述 最近在使用RecycerView的瀑布流布局,我想直接用ViewBinding取得item中的一个TextView然后根据position进行赋值。 比如我点击测试标题2,它在日志中应该能打印出测试标题2才对。 但是他却打印出“测试标题0” 按理来说标题应该更点击的位置对…...

基于EB工具的TC3xx_MCAL配置开发05_ADC模块硬件Pwm触发Demo配置
目录 1.概述2. Pwm相关配置2.1 PWM->General配置2.2 PWM->PwmChannel配置2.2.1 Reference Pwm通道配置2.2.2 触发ADC采集的Pwm通道配置3. ADC相关配置3.1 AdcHwExtTrigSelect配置4. MCU相关配置4.1 GTM配置4.1.1 McuGtmTomAllocationConf配置4.1.2 GtmTriggerForAdc配置1…...

Qt示例3:用Qt画一个温度计
示例1 以下是用Qt绘制一个简单的温度计的示例代码: #include <QPainter> #include <QWidget> #include <QApplication> class Thermometer : public QWidget { public:Thermometer(QWidget *parent 0); protected:void paintEvent(QPaintEvent …...
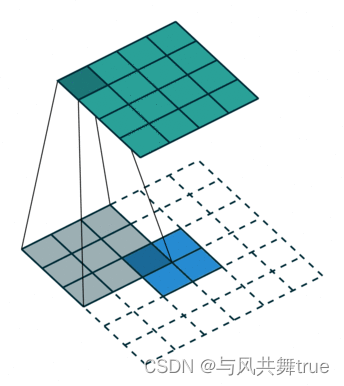
全卷积网络FCN
这里写目录标题全卷积网络FCN1、FCN2、FCN上采样3、 FCN具体实现过程转置卷积全卷积网络FCN 引用:http://t.csdn.cn/pDcjL 1、FCN FCN: FCN是对图像进行像素级的分类(也就是每个像素点都进行分类),从而解决了语义级别的图像分割…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...
