利用客户支持建立忠诚度和竞争优势
客户支持可以极大地改变您的业务;最细微、最微妙的差异都会使拥有一次性客户和拥有终身客户之间产生差异。在这篇博文中,我们将揭示客户对企业的忠诚度的三种核心类型,以及如何利用强大的客户支持工具和原则来提高理想的忠诚度并获得决定性的竞争优势。

一、客户忠诚度的 3 种类型
在福布斯的一篇文章中,专家建议企业应该从简单地将买家的旅程视为单行道。相反,他建议企业应该选择专注于建立客户忠诚度。他将客户忠诚度分为三个不同的类别。
1.习惯忠诚(手动驱动)
顾名思义,习惯性忠诚是基于客户的常规模式和生活方式。通常,这些选择是基于方便,可能不是最合乎逻辑/最理性的,并且通常几乎没有情感内容。例如,它选择离家最近的商店,或者他们习惯购买的品牌,因为它是最常见的。这些客户对品牌的忠诚度最低。
2.交易忠诚度(头部驱动)
交易忠诚更多地以头脑为中心,这是一种理性和合乎逻辑的决策方法。这些人根据提供的好处以及每家公司提供的优势或劣势来确定他们的忠诚度。他们会强调忠诚度计划、现金返还和折扣等内容。这些客户通常是忠诚的,直到他们找到提供更好的福利的替代方案。
3.情感忠诚(心驱)
最后一种类型的客户忠诚度是情感/心灵驱动的,最忠诚的客户在哪里。这些客户选择品牌是因为与他们的价值观保持一致,以及他们与品牌之间建立的情感纽带。这可以从那些建立了强大的忠诚度基础并不断为客户提供独特而引人入胜的体验的品牌身上看出。具有情感忠诚度的客户不仅会终生留在一个品牌上,而且他们通常会定期主动向朋友和家人推广它。
二、通过客户支持使您的业务与众不同
1、在客户服务中反映您的品牌形象和价值观
大多数公司都会努力创造品牌形象,并向客户展示他们的核心价值观,这些价值观是业务增长不可或缺的一部分。但是,当客户服务与整体品牌形象不相称时,这种形象就会分崩离析。太多的品牌忘记了客户互动的重要性至关重要,并留下了持久的印记。在将品牌形象和价值观与客户服务体验联系起来时,关注小细节至关重要。
比如:如果您是一个专注于创造有趣品牌体验的品牌,那么请确保客户服务体验的语气是有趣和乐观的。从长远来看,这些小而关键的细节会产生巨大的影响!
2、打造统一的全渠道客户支持体验
品牌需要确保您的客户支持在所有渠道中无缝衔接至关重要。这是因为当客户觉得整个体验是无缝的时,他们会觉得你在关注他们并且他们很重要。当客户通过 WhatsApp 与您联系并在一天后收到后续电子邮件时,他们会看到您的品牌正在关注他们。这是SaleSmartly(ss客服)这样的工具,可以集成您的所有客户渠道,使您能够创建前所未有的独特客户体验。
3、让您的客户感到被倾听。
没有什么比感觉被倾听更能帮助公司与您的品牌建立联系了。确保您始终在与您的品牌进行所有互动后为客户提供提供反馈的机会,然后确保您回复并对该反馈采取行动!客户反馈是最佳和最未充分利用的增长手段。
相关文章:

利用客户支持建立忠诚度和竞争优势
客户支持可以极大地改变您的业务;最细微、最微妙的差异都会使拥有一次性客户和拥有终身客户之间产生差异。在这篇博文中,我们将揭示客户对企业的忠诚度的三种核心类型,以及如何利用强大的客户支持工具和原则来提高理想的忠诚度并获得决定性的竞争优势。一…...

看他人代码小总结
针对几个功能类似的函数: 1.需要经常调试则定义一个参数比如is_debug来选择是否在调试,定义一些参数专门用于调试用,不用每次都修改这些参数,只需要修改is_debug这个参数; 2.把其中的变量(常量)单独拎出来放到一个文件…...
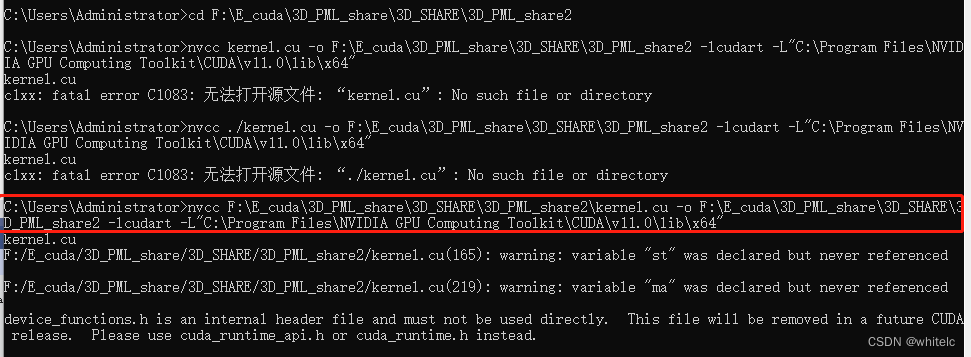
cudaMemGetInfo()函数cudaDeviceGetAttribute()函数来检查设备上的可用内存
使用CUDA Runtime API中的cudaMemGetInfo()函数来检查设备上的可用内存。该函数将返回当前可用于分配的总设备内存大小和当前可用于分配的最大单个内存块大小。 示例代码,演示了如何在分配内存之前和之后调用cudaMemGetInfo()函数来检查可用内存 size_t free_byte…...

【基础阶段】01中华人民共和国网络安全法
文章目录1 网络安全行业介绍2 什么是黑客和白帽子3 网络安全课程整体介绍4 网络安全的分类5 常见的网站攻击方式6 安全常见术语介绍7 《网络安全法》制定背景和核心内容8 《全国人大常委会关于维护互联网安全的决定》9《中华人民共和国计算机信息系统安全保护条例》10 《中华人…...

隐私计算领域大咖推荐,这些国内外导师值得关注
开放隐私计算 经过近一个月的信息收集,研习社已经整理了多位国内外研究隐私计算的导师资料。邻近考研复试,研习社希望小伙伴们能够通过本文整理的信息,选择自己心仪的老师,在研究生的路途上一帆风顺!1. 国内隐私计算导…...

009 uni-app之vue、vuex
vue.js 视频教程 vue3.js 中文官网 vue.js 视频教程 vue语法:https://uniapp.dcloud.net.cn/tutorial/vue-vuex.html vue2迁移到 vue3:https://uniapp.dcloud.net.cn/tutorial/migration-to-vue3.html Vuex Vuex 是一个专为 Vue.js 应用程序开发的…...
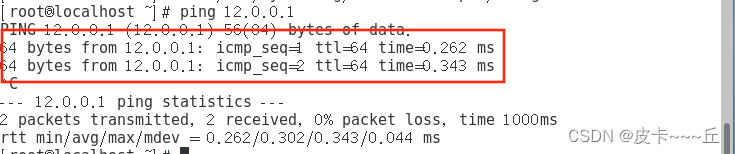
Linux防火墙——SNAT、DNAT
目录 NAT 一、SNAT策略及作用 1、概述 SNAT应用环境 SNAT原理 SNAT转换前提条件 1、临时打开 2、永久打开 3、SNAT转换1:固定的公网IP地址 4、SNAT转换2:非固定的公网IP地址(共享动态IP地址) 二、SNAT实验 配置web服务…...
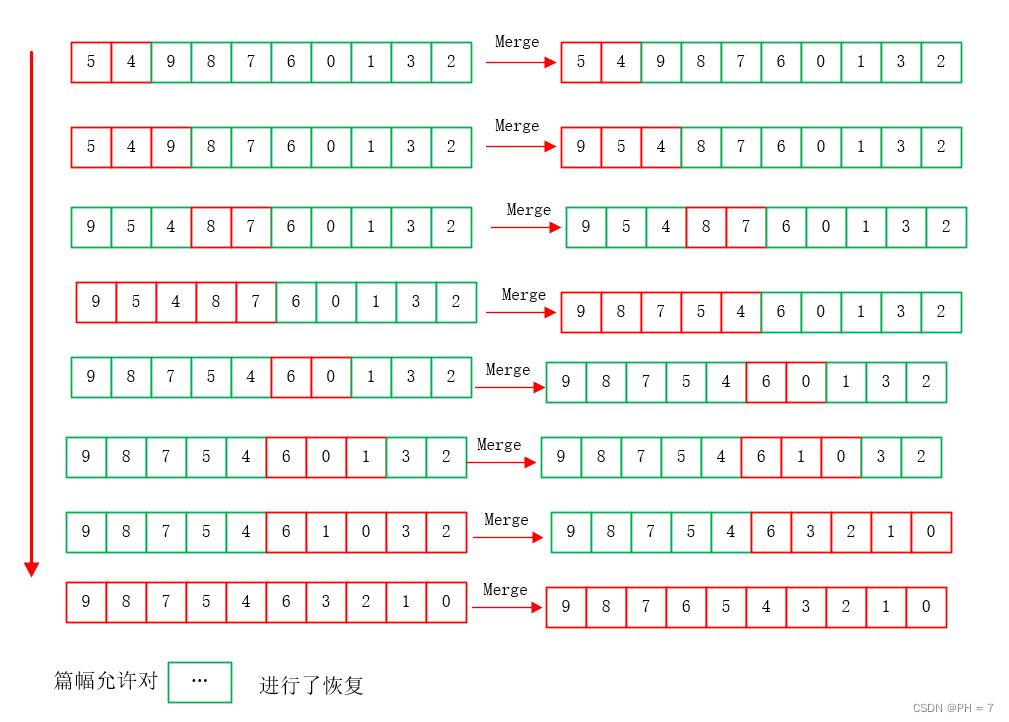
递归理解三:深度、广度优先搜索,n叉树遍历,n并列递归理解与转非递归
参考资料: DFS 参考文章BFS 参考文章DFS 参考视频二叉树遍历规律递归原理源码N叉树规律总结: 由前面二叉树的遍历规律和递归的基本原理,我们可以看到,二叉树遍历口诀和二叉树递推公式有着紧密的联系 前序遍历:F(x…...
MATLAB 2023a安装包下载及安装教程
[软件名称]:MATLAB 2023a [软件大小]: 12.2 GB [安装环境]: Win11/Win 10/Win 7 [软件安装包下载]:https://pan.quark.cn/s/8e24d77ab005 MATLAB和Mathematica、Maple并称为三大数学软件。它在数学类科技应用软件中在数值计算方面首屈一指。行矩阵运算、绘制函数和数据、实现算…...
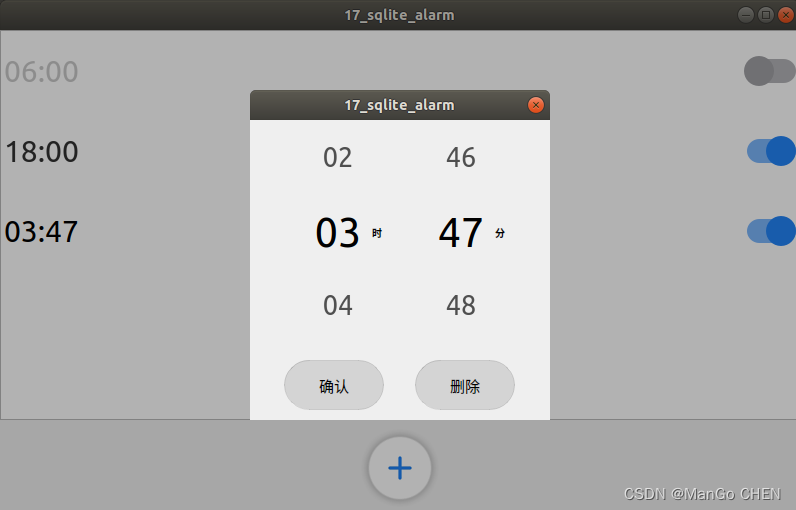
QT学习开发笔记(数据库之实用时钟)
数据库 数据库是什么?简易言之,就是保存数据的文件。可以存储大量数据,包括插入数据、更 新数据、截取数据等。用专业术语来说,数据库是“按照数据结构来组织、存储和管理数据的 仓库”。是一个长期存储在计算机内的、有组织的、…...
Docker常规安装简介
总体步骤 搜索镜像拉取镜像查看镜像启动镜像,服务端口映射停止容器移除容器 案例 安装tomcat docker hub上面查找tomcat镜像,docker search tomcat从docker hub上拉取tomcat镜像到本地 docker pull tomcatdocker images查看是否有拉取到的tomcat 使用tomcat镜像创…...
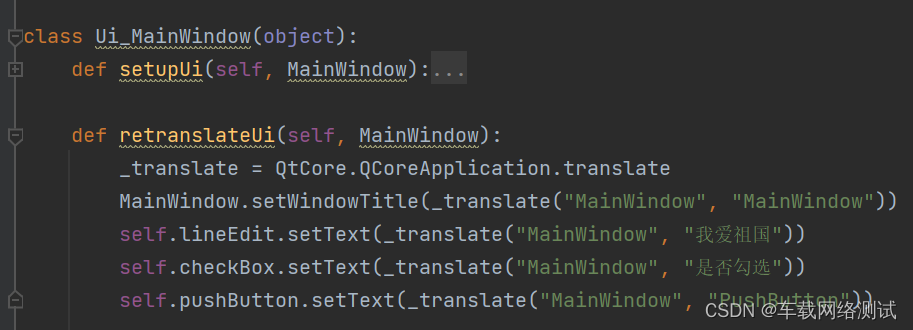
Python - PyQT5 - ui文件转为py文件
在QTdesigner图形化编辑工具中,有些控件我们是可以直接在编辑界面进行编辑的,有些是不可以编辑的,只能通过Python代码进行编辑,不过总体来说,所有能够通过图形化编辑界面可以编辑的,都可以通过Python语言实…...

分布式事务和分布式锁
1、关于分布式锁的了解? 原理:控制分布式系统有序的去对共享资源进行操作,通过互斥来保持一致性。 具备的条件: ①分布式环境下,一个方法在同一时间只能被一个机器的一个线程执行 ②高可用的获取锁和释放锁 ③高性能…...
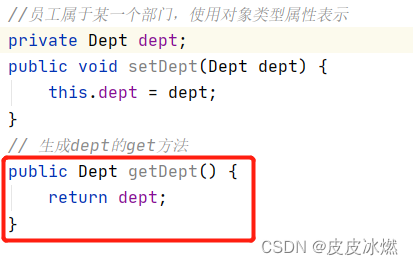
JAVA-4-[Spring框架]基于XML方式的Bean管理
1 Spring IOC容器 (1)IOC底层原理 (2)IOC接口(BeanFactory) (3)IOC操作Bean管理(基于XML) (4)IOC操作Bean管理(基于注释) 1.1 IOC概念 (1)控制反转(Inversion of Control),把对象的创建和对象之间的调用过程,交给Spring进行管理。 (2)使用IOC目的&…...
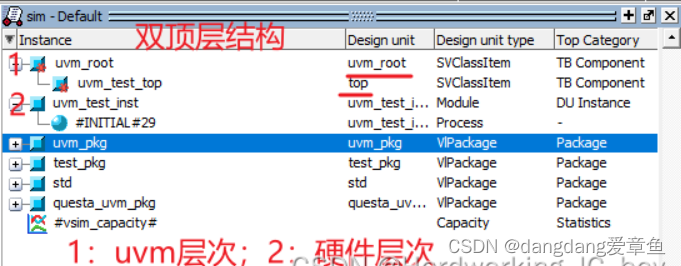
路科验证UVM入门与进阶详解实验0
一.代码编译 首先创建新项目,导入lab0 的UVM文件; 针对uvm_compile文件,先进行编译; module uvm_compile;// NOTE:: it is necessary to import uvm package and macrosimport uvm_pkg::*;include "uvm_macros.svh"in…...
Linux之Shell编程(1)
文章目录前言一、Shell是什么二、Shell脚本的执行方式脚本的常用执行方式三、Shell的变量Shell变量介绍shell变量的定义四、设置环境变量基本语法快速入门五、位置参数变量介绍●基本语法●位置参数变量六、预定义变量基本介绍基本语法七、运算符基本介绍基本语法前言 为什么要…...
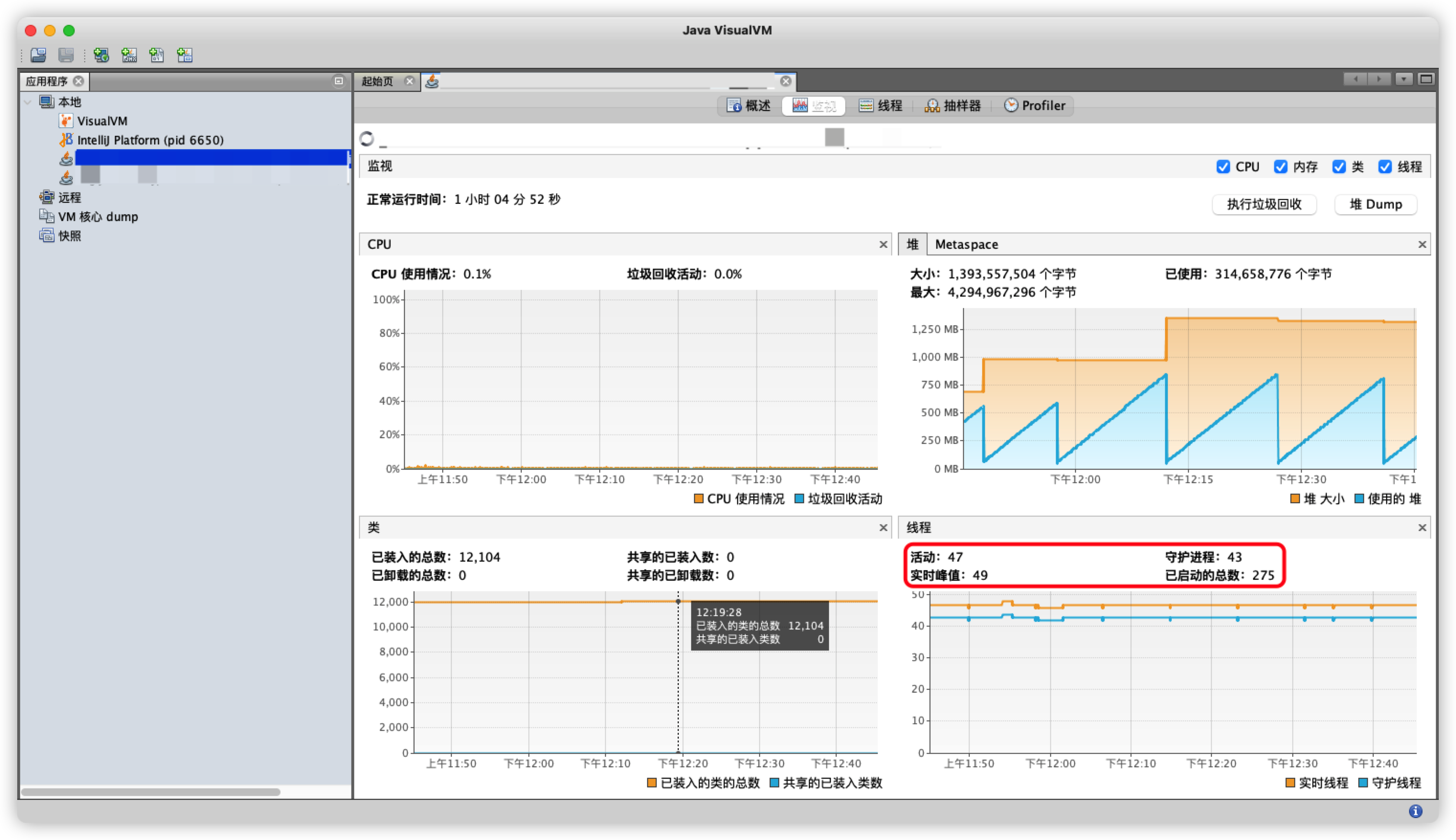
Java问题诊断工具——JVisualVM
这篇文章源自一次加班改bug的惨痛经历[,,_,,]:3负责的一个项目占用不断增加,差点搞崩服务器(╥﹏╥)……一下子有点懵,不能立刻确定是哪里导致的问题,所以决定好好研究下这个之前一直被我忽视的问题诊断工具🔧——JVisualVM嘿嘿我…...

Python3实现简单的车牌检测
导语Hi,好久不见~~~两周没写东西了,从简单的开始,慢慢提高文章水准吧,下一个月开始时间就会比较充裕了~~~利用Python实现简单的车牌检测算法~~~让我们愉快地开始吧~~~相关文件网盘下载链接: https://pan.baidu.com/s/1iJmXCheJoWq…...

基于支持向量机SVM多因子测量误差预测,支持向量机MATLAB代码编程实现
目录 支持向量机SVM的详细原理 SVM的定义 SVM理论 SVM应用实例,SVM的测量误差预测 代码 结果分析 展望 支持向量机SVM的详细原理 SVM的定义 支持向量机(support vector machines, SVM)是一种二分类模型,它的基本模型是定义在特…...

新农具时代,拼多多的进击与本分
这几年,乡村振兴被频频提及,核心就是经济振兴。但经济振兴,不能只靠政府,更要靠企业,政府引导、企业主导才能真正让农民、农村、农业长期受益。企业中,被寄予厚望的是电商企业。甚至,电商成为了…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...
