菜鸡勇闯第136场双周赛
菜鸡鼓足了勇气报名了力扣双周赛(后来复盘才知道双周赛更难一点,我真是头铁。。)
没想到还拿了个竞赛名次哈哈哈哈哈还在前50%,小力它真的,我哭死
为什么我本科被高数老师忽悠,去打了两年数模o(≧口≦)o
每一天都在想,我要是也接触acm,现在一定不会因为算法头大了吧(▼へ▼メ)
3238. 求出胜利玩家的数目
class Solution {public int winningPlayerCount(int n, int[][] pick) {int count = 0;HashMap<Integer, List<Integer>> map = new HashMap<>();for(int i = 0; i < pick.length; i++) {int player = pick[i][0];int ball = pick[i][1];if(map.containsKey(player)) {map.get(player).add(ball);}else {List<Integer> tmp = new ArrayList<>();tmp.add(ball);map.put(player, tmp);}}for(int key: map.keySet()) {List<Integer> tmplist = map.get(key);HashMap<Integer, Integer> tmpmap = new HashMap<>();for(int i = 0; i < tmplist.size(); i++) {int num = tmplist.get(i);tmpmap.put(num, tmpmap.getOrDefault(num, 0) + 1);}for(int key1: tmpmap.keySet()) {if(tmpmap.get(key1) > key) {count++;break;}}}return count;}
}
3239.最少翻转次数使二进制矩阵回文I
class Solution {public int minFlips(int[][] grid) {int row = grid.length;int col = grid[0].length;int[][] tmp1 = new int[row][col];int[][] tmp2 = new int[row][col];for(int i = 0; i < row; i++) {for(int j = 0; j < col; j++) {tmp1[i][j] = grid[i][j];tmp2[i][j] = grid[i][j];}}for(int i = 0; i < row; i++) {int left = 0;int right = col - 1;while(left < right) {int tmp = tmp1[i][left];tmp1[i][left] = tmp1[i][right];tmp1[i][right] = tmp;left++;right--;}}for(int j = 0; j < col; j++) {int upper = 0;int lower = row - 1;while(upper < lower) {int tmp = tmp2[upper][j];tmp2[upper][j] = tmp2[lower][j];tmp2[lower][j] = tmp;upper++;lower--;}}int res1 = 0;int res2 = 0;for(int i = 0; i < row; i++) {for(int j = 0; j < col; j++) {if(grid[i][j] != tmp1[i][j]) {res1++;}}}for(int i = 0; i < row; i++) {for(int j = 0; j < col; j++) {if(grid[i][j] != tmp2[i][j]) {res2++;}}}return (res1 >= res2) ? res2/2 : res1/2;}
}
3240.最少翻转次数使二进制矩阵回文II
public int minFlips(int[][] grid) {
// 记录一个dp的题解int m = grid.length, n = grid[0].length;int flips = 0;// 遍历左上角的四分之一矩阵,并与右上角、左下角、右下角的相应位置元素配对,计算每组需要的最小翻转次数for (int i = 0; i < m / 2; i++) {for (int j = 0; j < n / 2; j++) {// sum 代表当前 4 个对称元素的和int sum = grid[i][j] + grid[i][n - 1 - j] + grid[m - 1 - i][j] + grid[m - 1 - i][n - 1 - j];// 增加使这 4 个元素一致所需的最小flipflips += Math.min(sum, 4 - sum);}}boolean changed = false; // 用于标记是否已经在处理奇数行或列时进行了1/0 changeint countOne = 0; // 用于记录当奇数行或列时 1 的数量// 处理矩阵列数为奇数的情况,单独处理中间一列if (n % 2 == 1) {int colIndex = n / 2;for (int i = 0; i < m / 2; i++) {// 如果对称位置的元素不同,flip++, change = trueif (grid[i][colIndex] != grid[m - 1 - i][colIndex]) {flips++;changed = true;} else if (grid[i][colIndex] == 1) {// 如果两个位置的元素相同且为 1,countOne + 2countOne += 2;}}}// 处理矩阵行数为奇数的情况,单独处理中间一行if (m % 2 == 1) {int[] row = grid[m / 2];for (int j = 0; j < n / 2; j++) {// 如果对称位置的元素不同,flip++, change = trueif (row[j] != row[n - 1 - j]) {flips++;changed = true;} else if (row[j] == 1) {// 如果两个位置的元素相同且为 1,countcountOne += 2;}}}// 如果没有进行任何翻转且 countOne % 4 == 2,需要额外的翻转if (!changed && countOne % 4 == 2) {flips += 2;}// 如果矩阵行列都为奇数,需要检查中心元素if (m % 2 == 1 && n % 2 == 1 && grid[m / 2][n / 2] == 1) {flips++;}return flips;
}3241.标记所有节点需要的时间
class Solution {// 记录一个换根DP的解法int[] head, nxt, to;// first 当前节点最长耗时// firstNo 最长耗时子节点编号// second 当前节点第二大耗时int[] first, firstNo, second;int[] ans;public int[] timeTaken(int[][] edges) {int n = edges.length + 1;head = new int[n];Arrays.fill(head, -1);nxt = new int[n << 1];to = new int[n << 1];for (int i = 0, j = 2; i < n - 1; i++) {int u = edges[i][0], v = edges[i][1];nxt[j] = head[u]; head[u] = j; to[j++] = v;nxt[j] = head[v]; head[v] = j; to[j++] = u;}first = new int[n];firstNo = new int[n];second = new int[n];ans = new int[n];dfs(-1, 0);dp(-1, 0, 0);return ans;}// 换根 DP:维护之前节点到 u 的最长耗时 —— preFirstpublic void dp(int f, int u, int preFirst) {for (int e = head[u], v; e != -1; e = nxt[e]) {v = to[e];if (f != v) {// 如果 v 为 firstNo[u],表示 v 为最长耗时子节点,取 second[u] 进行比较// 否则,取 first[u] 进行比较// 同时,在得到 v 的所有之前节点到 u 的最长耗时后,该耗时还需要加上 u → v 的耗时// 从而得到 v 之前的所有节点到 v 的最长耗时int pf = Math.max(preFirst, v == firstNo[u] ? second[u] : first[u]) + ((u & 1) == 0 ? 2 : 1);ans[v] = Math.max(ans[v], pf);dp(u, v, pf);}}}public void dfs(int f, int u) {for (int e = head[u], v; e != -1; e = nxt[e]) {v = to[e];if (f != v) {dfs(u, v);// t 表示 u → v 和 v 的所有后继节点的最长耗时int t = first[v] + ((v & 1) == 0 ? 2 : 1);if (first[u] < t) {second[u] = first[u];first[u] = t;firstNo[u] = v;} else if (second[u] < t) {second[u] = t;}}}// 将每个结点答案初始化为当前节点最长耗时ans[u] = first[u];}
}
相关文章:

菜鸡勇闯第136场双周赛
菜鸡鼓足了勇气报名了力扣双周赛(后来复盘才知道双周赛更难一点,我真是头铁。。) 没想到还拿了个竞赛名次哈哈哈哈哈还在前50%,小力它真的,我哭死 为什么我本科被高数老师忽悠,去打了两年数模o(≧口≦)o 每…...

趋动科技陈飞:从小模型到大模型,AI时代下的数据中心建设
自AI大模型横空出世,不断推动着AI从学术界到产业界向大众破圈,新的时代正在来临。11月15-16日,由CDCC主办的“2023第11届数据中心标准大会”在北京国家会议中心盛大开幕。 本届大会的主题围绕“AI时代 重塑未来”,聚焦数据中心领…...

yolo v8 + flask部署到云服务器,以及问题记录
环境安装 1、运行项目报错:no python application found, check your startup logs for errors 在云服务器pytorch版本安装错了,安装了GPU版本,需要安装CPU版本 # CPU only 使用下面这段代码避免出现第二个错误 pip install torch2.3.1 to…...

【科研必备插件】easyscholar如何使文章显示期刊影响因子与分区等级
简要介绍 EasyScholar 是一个微软 Edge 浏览器的扩展程序,可以显示会议、期刊等级。可支持在各大论文搜索网站,显示各种期刊、会议等级排名 要想你的知网页面如下图所示,快来获取安装,快速科研有方法 插件安装教程 ①打开浏览器…...

UE5 UrlEncode转换
调用接口时用到了 UFUNCTION(BlueprintPure, Category "FuncLib", meta (Keywords "URL1"))static FString StringToURLEncode(const FString& str1);FString UBasicFuncLib::StringToURLEncode(const FString& str1){return FGenericPlatformH…...
的正确使用方法)
【QML】Qt.rgba()的正确使用方法
1. 问题 设置颜色 color: Qt.rgba(65,105,225,255) ,应该是蓝色,却显示白色。 2. 正确方法 //正确代码 color: Qt.rgba(65/255, 105/255, 225/255, 255/255)...

centos7.9 docker安装
1、不要通过yum直接安装 具体原因: CentOS 6 因内核太旧,即使支持安装 docker,但会有各种问题,不建议安装CentOS 7 的 extras 源虽然可以安装 docker,但包比较旧,建议从官方源或镜像源站点下载安装 docke…...

spring操作数据库
xml版 程序结构 配置文件 dbUtil-阿帕奇提供操作数据库的插件 核心类:QueryRunner .query() 查询 .update() 增删改 <dependencies><!-- spring --><dependency><groupId>org.springframework</groupId><artifactId>spri…...

Apache Flink中TaskManager,SubTask,TaskSlot,并行度之间的关系
Apache Flink 中Application 与 Job 一个完整的Flink Application 一般组成如下: Source 数据来源Transformation 数据转换处理等Sink 数据传输 Flink 中一个或者多个Operator(算子)组合对数据进行转换形成一个 Transformation,一…...

马斯克xAI新计划:人工智能模型Grok 2测试版即将发布
特斯拉CEO马斯克在X平台上表示,人工智能模型Grok 2测试版即将发布。Grok,作为xAI公司的明星大语言模型,其首代产品Grok 1已凭借神经演化计算与深度学习技术的深度融合,展现了超乎想象的学习速度与智能深度,赢得了业界的…...

【机器人学】6-4.六自由度机器人运动学参数辨识-机器人精度验证【附MATLAB代码】
前言 前两个章节以及完成了机器人参数辨识。 【机器人学】6-1.六自由度机器人运动学参数辨识-辨识数学模型的建立 【机器人学】6-2.六自由度机器人运动学参数辨识-优化方法求解辨识参数 这里我们认为激光测量仪测量到的数据为机器人实际到达的位置,而机器人理论到…...
分销商城小程序系统渠道拓展
线上卖货渠道很多,想要不断提高营收和新客获取,除了自己和工具本身努力外,还需要其他人的帮助来提高商城店铺的整体销量。 搭建saas商城系统网站/小程序,后台上货,设置支付、配送、营销、精美模板商城装修等内容&…...

WPF篇(14)-ProgressBar进度条+Calendar日历控件+DatePicker日期控件
ProgressBar进度条 ProgressBar进度条通常在我们执行某个任务需要花费大量时间时使用,这时可以采用进度条显示任务或线程的执行进度,以便给用户良好的使用体验。 ProgressBar类定义 public class ProgressBar : RangeBase {public static readonly De…...
链表高频题目和必备技巧
链表高频题目和必备技巧 1. 链表类题目注意点 1,如果笔试中空间要求不严格,直接使用容器来解决链表问题 2,如果笔试中空间要求严格、或者在面试中面试官强调空间的优化,需要使用额外空间复杂度**O(1)**的方法 3,最…...

Vue3详细介绍,正则采集器所用前端框架
Vue3 引入了一个全新的响应式系统,它是基于ES6的Proxy特性构建的。这个系统使得 Vue 能够更加高效地追踪数据的变化,并在数据发生变化时自动更新DOM。响应式系统的核心是"可观察",当数据变化时,视图会响应这些变化并重新…...
)
数据集--COCO2017(快速下载)
1、数据集介绍 数据集官网:https://cocodataset.org/#home COCO(Common Objects in Context)数据集是计算机视觉领域中最广泛使用的数据集之一,主要用于目标检测、分割和图像标注任务。COCO 数据集由 Microsoft 发布,…...
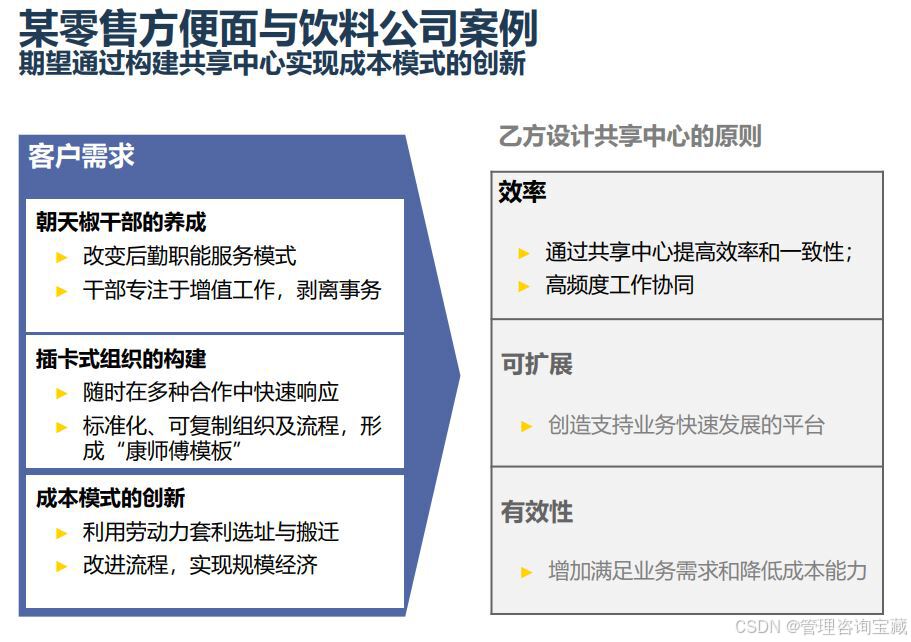
【管理咨询宝藏159】顶级咨询公司人力三支柱建设方案思路
阅读完整版报告内容,请搜索VV号“管理咨询宝藏”。 【管理咨询宝藏159】顶级咨询公司人力三支柱建设方案思路 【格式】PDF版本 【关键词】人力咨询、三支柱、人力体系 【核心观点】 - 集团总部制定全集团共享中心总体规划路径,组织并负责实施与推广。各…...

跨时钟域总结
跨时钟域总结 秋招学习跨时钟域 总结一下吧 异步电路 设计中有两个频率不同的时钟(也可能多个),而有数据在两组时钟之间传输 单bit跨时钟域 慢时钟域数据-> 快时钟域 方法 : 使用两个锁存器 (打两拍) 数据跨时钟域同步过程中,脉冲宽度会改变,不影响同步结…...

富婆和富公子都在看的负载均衡和Haproxy大全
一.负载均衡 1.1:什么是负载均衡 负载均衡: Load Balance ,简称 LB ,是一种服务或基于硬件设备等实现的高可用反向代理技术,负载均 衡将特定的业务(web 服务、网络流量等 ) 分担给指定的一个或多个后端特定的服务器或…...

VScode找python环境 (conda)
第一步 CtrlshiftP 第二步 框框里输入:Python:Select Interpreter...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
