DFS(深度优先搜索)和BFS(宽度优先搜索)

目录
DFS(深度优先搜索)
全排列的DFS解法
利用DFS递归构建二进制串和递归树的结构剖析
DFS--剪枝
DFS例题--整数划分
BFS(宽度优先搜索)
全排列的BFS解法
DFS(深度优先搜索)
深度优先搜索(Depth First Search,DFS)是十分常见的图搜索方法之一。深度优先搜索会沿着一条路径一直搜索下去,在无法搜索时,回退到刚刚访问过的节点。深搜优先搜索的本质上就是持续搜索,遍历了所有可能的情况。DFS搜索的流程是一个树的形式,每次一条路走到低。
全排列的DFS解法

public class DFS {public static void main(String[] args) {DFS(0, "", 3);}public static void DFS(int depth, String ans, int n) {if (depth == n) {//深度等于n时就输出System.out.print(ans + " ");return;}for (int i = 1; i <= n; i++) {DFS(depth + 1, ans + i, n); }}
}如果不对其进行剪枝操作,就会将所有的子叶全部输出

所以在需要要求全排列的情况下我们就需要进行剪枝,也就是对递归循环进行判断
public class DFS {public static void main(String[] args) {DFS(0, "", 3);}public static void DFS(int depth, String ans, int n) {if (depth == n) {//深度等于n时就输出System.out.print(ans + " ");return;}for (int i = 1; i <= n; i++) {if (! ans.contains("" + i)) {//目前已经生成的ans串用过的不能再用(剪枝)DFS(depth + 1, ans + i, n);}//public boolean contains(CharSequence s)// 当且仅当此字符串包含指定的 char 值序列时,返回 true。}}
}这样得到的结果就是全排列后的结果了
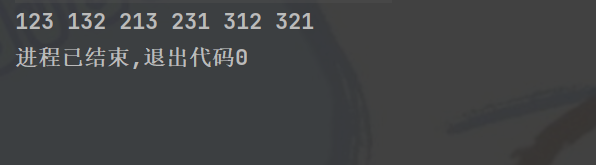
利用DFS递归构建二进制串和递归树的结构剖析
二进制串0000 -> 1111的所有可能
public class binaryStringRecurrence {public static void main(String[] args) {DFS(0, "");//从0层开始}public static void DFS(int depth, String binary) {//depth为深度,binary为求出的二进制串System.out.printf("%sdg(%d, %s)\n", Lpad(depth), depth, binary);//用来查看各个节点if (depth == 4) {//深度为4的时候输出字符串System.out.println(binary);return;}//每次开枝散叶都需要开2支,左边补0,右边补1DFS(depth + 1, binary + "0");DFS(depth + 1, binary + "1");}public static String Lpad(int n) {//用来打印空格String ans = "";for (int i = 1; i <= n; i++) {ans += " ";}return ans;}
}代码执行流程,可以看出DFS递归的流程以及开枝散叶的方式
dg(0, )
dg(1, 0)
dg(2, 00)
dg(3, 000)
dg(4, 0000)
0000
dg(4, 0001)
0001
dg(3, 001)
dg(4, 0010)
0010
dg(4, 0011)
0011
dg(2, 01)
dg(3, 010)
dg(4, 0100)
0100
dg(4, 0101)
0101
dg(3, 011)
dg(4, 0110)
0110
dg(4, 0111)
0111
dg(1, 1)
dg(2, 10)
dg(3, 100)
dg(4, 1000)
1000
dg(4, 1001)
1001
dg(3, 101)
dg(4, 1010)
1010
dg(4, 1011)
1011
dg(2, 11)
dg(3, 110)
dg(4, 1100)
1100
dg(4, 1101)
1101
dg(3, 111)
dg(4, 1110)
1110
dg(4, 1111)
1111进程已结束,退出代码0
DFS--剪枝
剪枝是DFS中的一个判断技巧,就是把不会产生答案的或者不必要的的枝条剪掉。剪枝的关键是剪哪一条枝,在哪个地方减。
将整数n分成k份,每份不能为空,任意两种划分方案不能相同(不考虑顺序)
例如:n = 7,k = 3,下面三种划分方案被认为是相同的
115 151 511
import java.util.Scanner;public class nDivideK {public static int ans;//记录成功方案的次数public static int cnt;//记录DFS调用的次数public static void main(String[] args) {Scanner scanner = new Scanner(System.in);while (scanner.hasNext()) {int n = scanner.nextInt();//被划分数int k = scanner.nextInt();//规定划分份数DFS(n, k, 1, "");//i初始为1,因为第一次最小可用值就是1System.out.println("方案数为:" + ans);System.out.println("DFS调用的次数为:" + cnt);}}/*** 整数n划分k份的方案* @param n 被划分数* @param k 规定划分份数* @param min 保证构造非降序,如 1 1 5和 5 1 1是 等价的。表示目前被拆分使用的最大数,下次拆分可用的最小值* @param fangan 记录划分方案次数*/public static void DFS(int n, int k, int min, String fangan) {cnt++;//只要DFS被调用cnt就自增if (k == 1 && min <= n) {//这里min需要小于等于n,要不无法继续拆解ans++;//找到正确的方案,ans就自增System.out.println(fangan + n);return;}if (min * k > n) return;//剪枝//开枝散叶for (int i = min; i <= n ; i++) {DFS(n - i, k - 1, i, fangan + i +"+");//n-i为拆分后的数,k-1为剩余的拆分次数,i为下次可用的最小值}}
}运行结果:
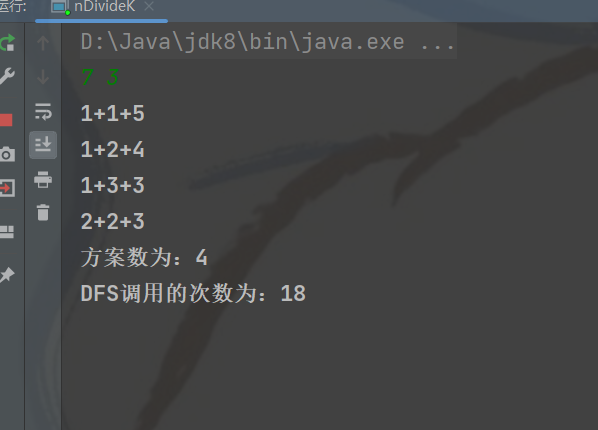
DFS例题--整数划分
一个整数可以划分成若干个不超过自己的整数之和的形式,例如:
4
4=1+1+1+1
4=1+1+2
4=1+3
4=2+2
4=4
总共有5种划分形式,约定
1)这些加数必须遵循从小到大原则
2)4=1+3和4=3+1当做一种划分
public class DFSIntSplit {public static void main(String[] args) {int n = 4;DFS(n, 0, 0, "");}/**** @param n 被拆分的数* @param nowget 目前已经得到的值* @param maxused 记录目前拆分已经使用的最大值* @param ans 拆分方案*/public static void DFS(int n, int nowget, int maxused, String ans) {if (nowget == n) {//当已经得到的值等于被拆分的数时就结束System.out.println(n + "=" + ans);return;}//开枝散叶for (int i = 1; i <= n - nowget ; i++) {//需要累加到n,已经累加到了nowget,所以要n - nowgetif (i >= maxused && i == n - nowget) {//i必须大于当前拆分的最大值才可以继续递归//如果是最后一次循环(i==n-nowget),那么ans + i就不需要再加 "+" 了DFS(n, nowget + i, i, ans + i);} else if (i >= maxused) {DFS(n, nowget + i, i, ans + i + "+");}}}
}得到结果:
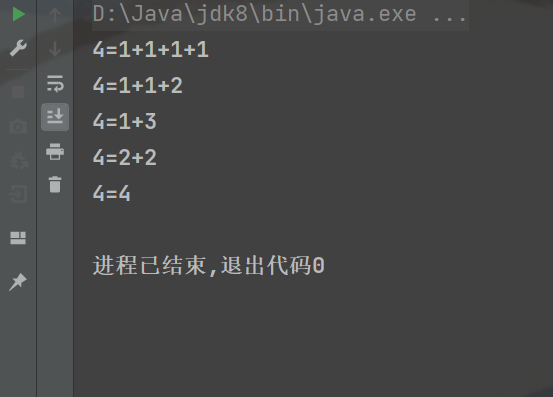
BFS(宽度优先搜索)
宽度优先搜索(Breadth First Search,BFS)它是从初始结点开始,应用产生式规则和控制策略生成第一层结点,同时检查目标结点是否在这些生成的结点中。若没有,再用产生式规则将所有第一层结点逐一拓展,得到第二层结点,并逐一检查第二层结点是否包含目标结点。若没有,再用产生式规则拓展第二层结点。如此依次拓展,检查下去,直至发现目标结点为止。如果拓展完所有结点,都没有发现目标结点,则问题无解。
全排列的BFS解法
BFS求全排列需要用到队列,首先将1 2 3三个根节点放入队列,每次弹出一个队列头,同时将此队列头对应的两个子叶入列。
import java.util.LinkedList;
import java.util.Queue;public class BFS {public static void main(String[] args) {int n = 3;Queue<String> queue = new LinkedList<String>();for (int i = 1; i <= n; i++) {//将1 2 3入队列queue.offer("" + i);}while (!queue.isEmpty()) {//如果队列不为空就循环//public boolean isEmpty()// 当且仅当 length() 为 0 时返回 true。//返回:如果 length() 为 0,则返回 true;否则返回 false。String head = queue.poll();//弹出列头for (int i = 1; i <= n; i++) {if (head.contains("" + i)) continue;//如果head包含i,就不扩展了String son = head + i;//子叶等于列头+iif (son.length() == n) System.out.println(son);//长度为n说明就产生了三阶的全排列了,就输出else queue.offer(son);//否则就将son入队列}}}
} 
相关文章:

DFS(深度优先搜索)和BFS(宽度优先搜索)
目录 DFS(深度优先搜索) 全排列的DFS解法 利用DFS递归构建二进制串和递归树的结构剖析 DFS--剪枝 DFS例题--整数划分 BFS(宽度优先搜索) 全排列的BFS解法 DFS(深度优先搜索) 深度优先搜索(Depth First Search&…...

Redis缓存穿透、击穿、雪崩问题及解决方法
系列文章目录 Spring Cache的使用–快速上手篇 分页查询–Java项目实战篇 全局异常处理–Java实战项目篇 完善登录功能–过滤器的使用 上述只是部分文章,对该系列文章感兴趣的可以查看我的主页哦 文章目录系列文章目录前言一、缓存穿透1.1 问题引入1.2 解决方法1.…...

HAL库 STM32 串口通信
一、实验条件将STM32的PA9复用为串口1的TX,PA10复用为串口1的RX。STM32芯片的输出TX和接收RX与CH340的接收RX和发送TX相连(收发交叉且PCB上默认没有相连,所以需要用P3跳线帽进行手动连接),CH340的另一端通过USB口引出与…...

2023-第十四届蓝桥杯冲刺计划!
💬前言 💡本文以目录形式列举大纲,可根据题目点击跳转 🌈冲刺阶段目的:把握高频重点,结合基础算法和常考题型总结,用真题进行模拟练习 根据自己的能力熟练目前已掌握的算法,不会的还可以暴力 ⏳最后三个星期大家一起冲…...
内网渗透基础知识
一、内网概述 内网也指局域网,是指在某一区域内又多台计算机互联成的计算机组。一般是方圆几千米内,局域网可以实现文件管理,应用软件共享,打印机共享,工作组内的历程安排,电子邮件和传真通信服务等功能。…...

鸟哥的Linux私房菜 正则表示法与文件格式化处理
第十一章、正则表示法与文件格式化处理 https://linux.vbird.org/linux_basic/centos7/0330regularex.php 简体版 http://cn.linux.vbird.org/linux_basic/0330regularex.php 11.2.2 grep的一些高级选项 例题一、搜索特定字符串 例题二、利用中括号 [] 来搜寻集合字符 例题四…...
1630.等差子数组
1630. 等差子数组 难度中等 如果一个数列由至少两个元素组成,且每两个连续元素之间的差值都相同,那么这个序列就是 等差数列 。更正式地,数列 s 是等差数列,只需要满足:对于每个有效的 i , s[i1] - s[i] …...
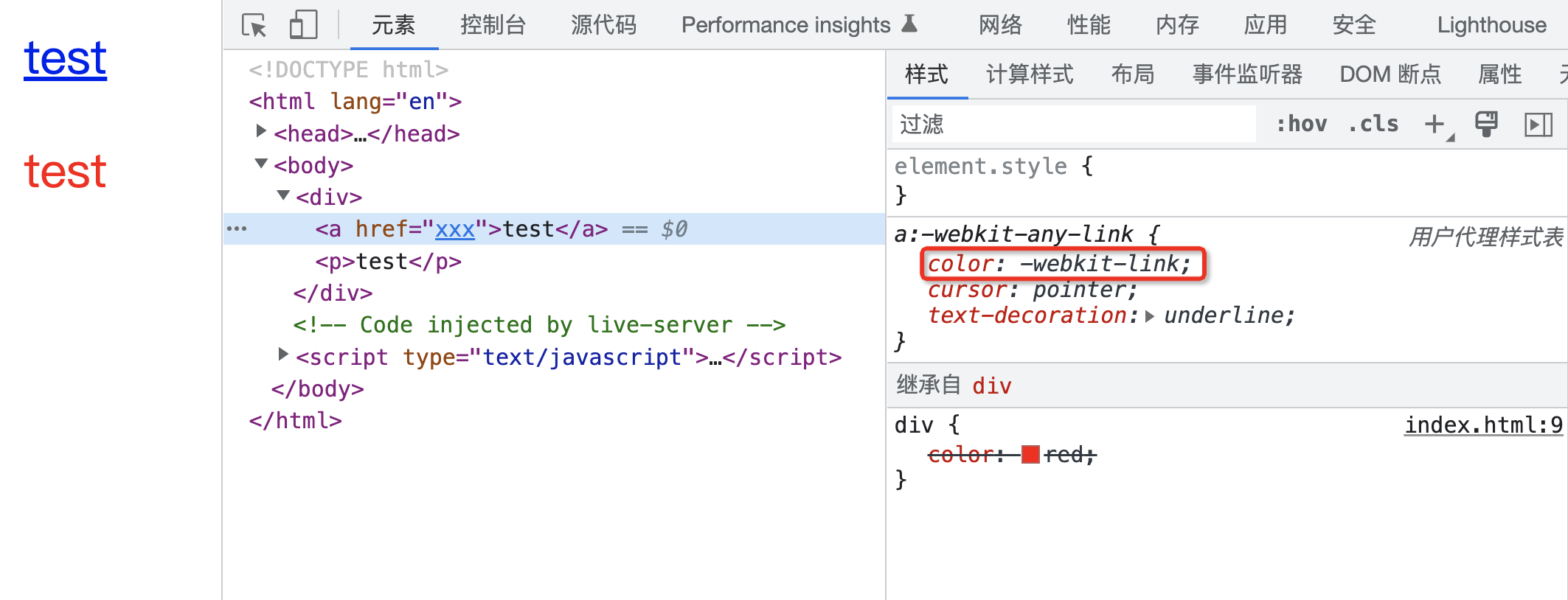
CSS 属性计算过程
CSS 属性计算过程 你是否了解 CSS 的属性计算过程呢? 有的同学可能会讲,CSS属性我倒是知道,例如: p{color : red; }上面的 CSS 代码中,p 是元素选择器,color 就是其中的一个 CSS 属性。 但是要说 CSS 属…...

ThinkPHP02:路由
ThinkPHP02:路由一、路由定义二、变量规则三、路由地址四、路由参数五、路由分组六、MISS七、资源路由八、注解路由九、URL生成一、路由定义 路由默认开启,在 config/app.php 中可以关闭路由。 路由配置在 config/route.php 中,路由定义在 r…...

制作简单进销存管理系统(C#)
实验三:制作简单进销存管理系统 任务要求: 在进销存管理系统中,商品的库存信息有很多种类,比如商品型号、商品名称、商品库存量等。在面向对象编程中,这些商品的信息可以存储到属性中,然后当需要使用这些…...
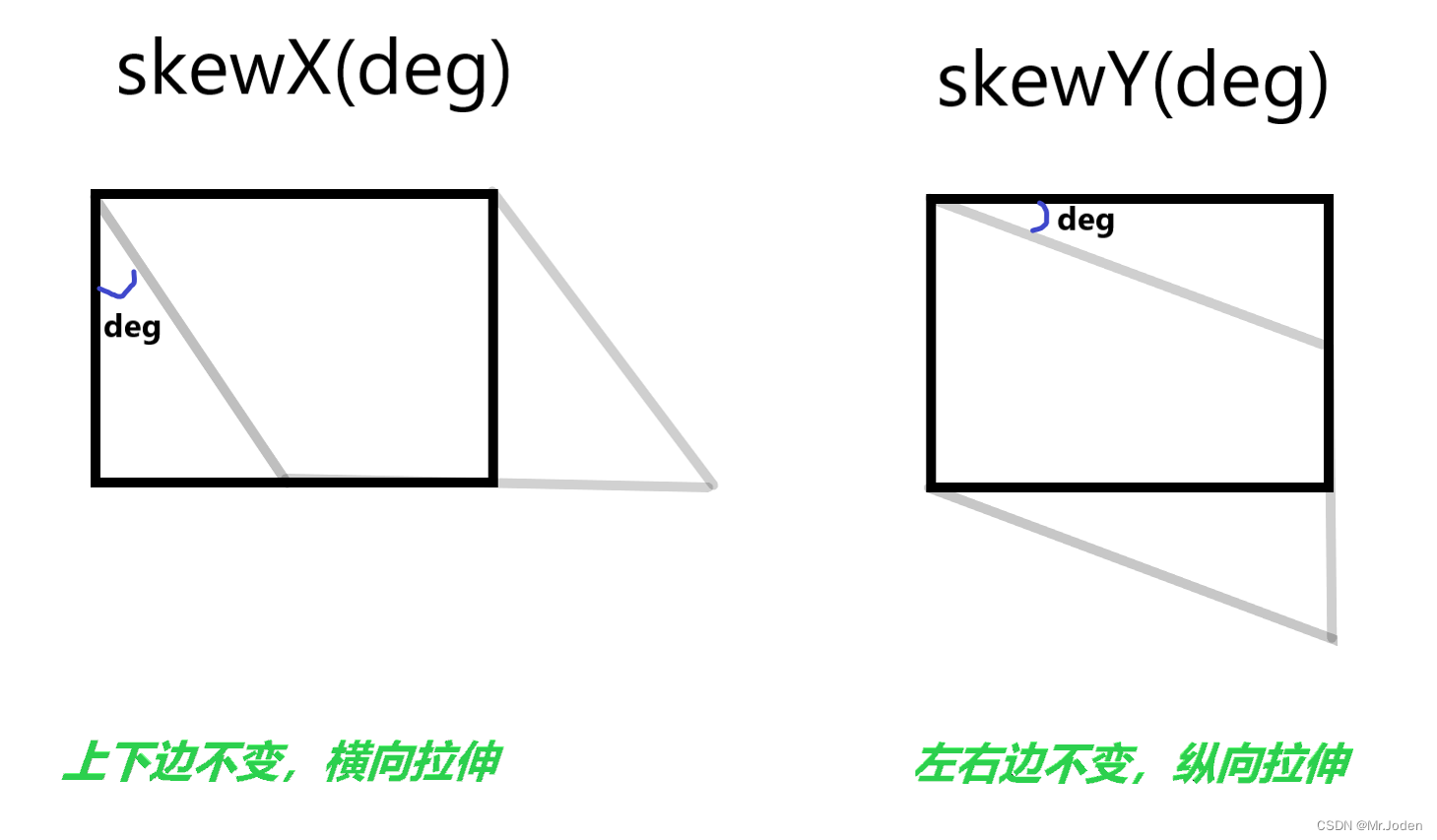
css总结9(过渡和2D变换)
目录 过渡 2D变换 3D变换 过渡 属性结构图 过渡补充 ### 过渡多个元素样式属性 transition:style1 duration , style2 duration,...; ### 过渡所有属性 transition: all duration; 简单示例 ### 移入时改变长度且加入过渡效果 div { width:100px; height:100px; …...
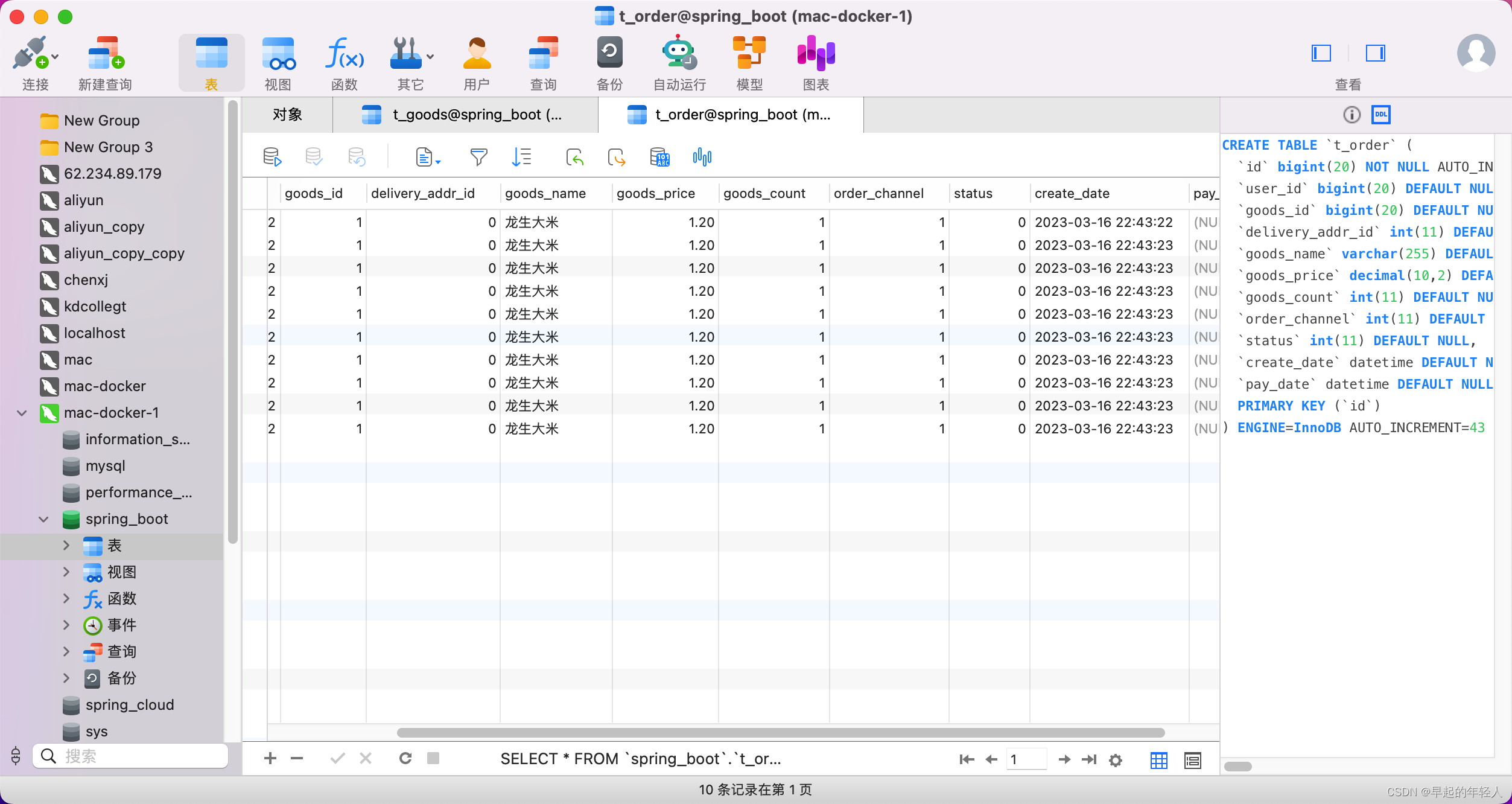
SpringBoot 结合RabbitMQ与Redis实现商品的并发下单【SpringBoot系列12】
SpringCloud 大型系列课程正在制作中,欢迎大家关注与提意见。 程序员每天的CV 与 板砖,也要知其所以然,本系列课程可以帮助初学者学习 SpringBooot 项目开发 与 SpringCloud 微服务系列项目开发 1 项目准备 SpringBoot 整合 RabbitMQ 消息队…...

【python进阶】序列切片还能这么用?切片的强大比你了解的多太多
📚引言 🙋♂️作者简介:生鱼同学,大数据科学与技术专业硕士在读👨🎓,曾获得华为杯数学建模国家二等奖🏆,MathorCup 数学建模竞赛国家二等奖🏅,…...
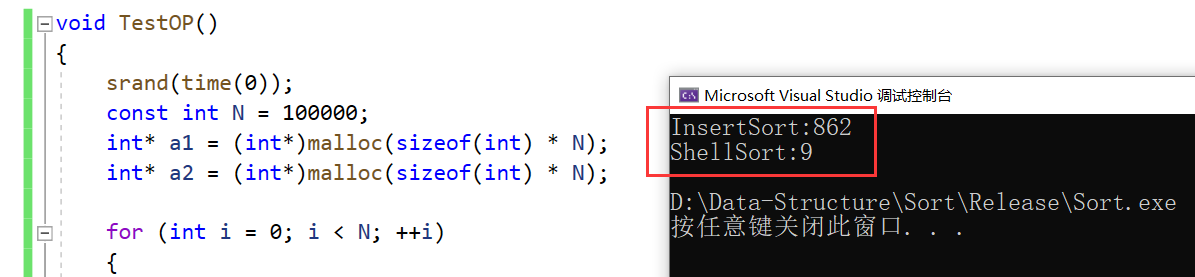
[数据结构]直接插入排序、希尔排序
文章目录排序的概念和运用排序的概念排序运用常见的排序算法常见的排序算法直接插入排序希尔排序性能对比排序的概念和运用 排序的概念 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操…...

CNN、LeNet、AlexNet、VGG、GoogLeNet、RCNN、Fast RCNN、Faster RCNN、YOLO、YOLOv2、SSD等的关系
卷积神经网络的现状1943年美国数学家提出人工智能1949年心理学家建立神经元模型1957年弗兰克提出 感知器人工神经网络模型1980年建立多层感知器模型1984日本学者提出卷积神经网络原始模型神经感知机1998年提出LeNet-5卷积神经网络,并发展了其在音符和字符上的优势20…...
)
IO-day1-(fscanf、fprintf.........)
作业一、有一个usr.txt的文件,其中存储着用户的账户和密码,格式如下:zhangsan aaaalisi bbbbb空格前面是账户,空格后面是密码,一行一个账户、密码要求如下:从终端获取一个账户名和密码判断是否能够登录成功…...
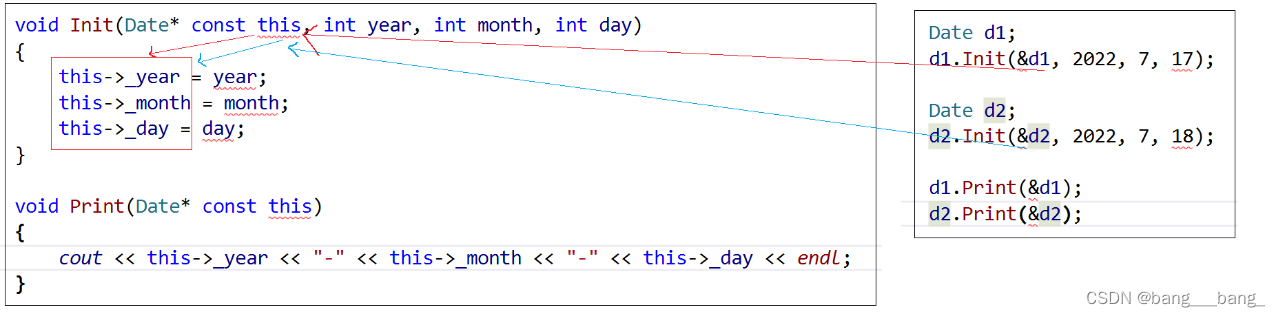
C++类和对象(上篇)
目录 1.类的定义 2.类的访问限定符及封装 2.1类的访问限定符 2.2封装 3.类的作用域 4.类的实例化 5.类的大小 6.this 指针 1.类的定义 class className {// 类体:由成员函数和成员变量组成}; // 一定要注意后面的分号 class为定义类的关键字,Clas…...
解决Xshell无法连接Kali Linux 2020.1(2019.3)版本
使用Xshell远程终端工具连接虚拟机的Kali Linux却提示连接不上原因:Kali Linux默认没有打开SSH远程登录,SSH就是一种网络协议,用于加密的远程登录,所以在没有打开SSH协议之前是无法使用Xshell连接Kali Linux的。解决办法ÿ…...
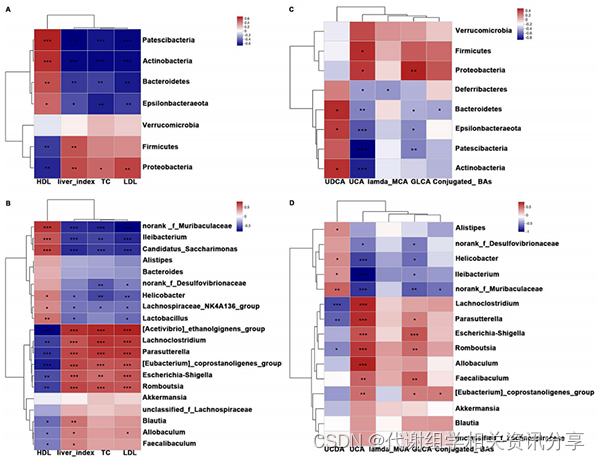
项目文章 | 缓解高胆固醇血症 ,浒苔多糖如何相助?
文章标题:Polysaccharides from Enteromorpha prolifera alleviate hypercholesterolemia via modulating the gut microbiota and bile acid metabolism 发表期刊:Food & Function 影响因子:6.317 作者单位:福建医科大…...
Linux使用宝塔面板搭建网站,并内网穿透实现公网访问
文章目录前言1. 环境安装2. 安装cpolar内网穿透3. 内网穿透4.固定http地址5. 配置二级子域名6.创建一个测试页面前言 宝塔面板作为简单好用的服务器运维管理面板,它支持Linux/Windows系统,我们可用它来一键配置LAMP/LNMP环境、网站、数据库、FTP等&…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...

Linux操作系统共享Windows操作系统的文件
目录 一、共享文件 二、挂载 一、共享文件 点击虚拟机选项-设置 点击选项,设置文件夹共享为总是启用,点击添加,可添加需要共享的文件夹 查询是否共享成功 ls /mnt/hgfs 如果显示Download(这是我共享的文件夹)&…...

【Vue】scoped+组件通信+props校验
【scoped作用及原理】 【作用】 默认写在组件中style的样式会全局生效, 因此很容易造成多个组件之间的样式冲突问题 故而可以给组件加上scoped 属性, 令样式只作用于当前组件的标签 作用:防止不同vue组件样式污染 【原理】 给组件加上scoped 属性后…...

WinUI3开发_使用mica效果
简介 Mica(云母)是Windows10/11上的一种现代化效果,是Windows10/11上所使用的Fluent Design(设计语言)里的一个效果,Windows10/11上所使用的Fluent Design皆旨在于打造一个人类、通用和真正感觉与 Windows 一样的设计。 WinUI3就是Windows10/11上的一个…...

ubuntu清理垃圾
windows和ubuntu 双系统,ubuntu 150GB,开发用,基本不装太多软件。但是磁盘基本用完。 1、查看home目录 sudo du -h -d 1 $HOME | grep -v K 上面的命令查看$HOME一级目录大小,发现 .cache 有26GB,.local 有几个GB&am…...

Yolo11改进策略:Block改进|FCM,特征互补映射模块|AAAI 2025|即插即用
1 论文信息 FBRT-YOLO(Faster and Better for Real-Time Aerial Image Detection)是由北京理工大学团队提出的专用于航拍图像实时目标检测的创新框架,发表于AAAI 2025。论文针对航拍场景中小目标检测的核心难题展开研究,重点解决…...
