1630.等差子数组
1630. 等差子数组
难度中等
如果一个数列由至少两个元素组成,且每两个连续元素之间的差值都相同,那么这个序列就是 等差数列 。更正式地,数列 s 是等差数列,只需要满足:对于每个有效的 i , s[i+1] - s[i] == s[1] - s[0] 都成立。
例如,下面这些都是 等差数列 :
1, 3, 5, 7, 9 7, 7, 7, 7 3, -1, -5, -9
下面的数列 不是等差数列 :
1, 1, 2, 5, 7
给你一个由 n 个整数组成的数组 nums,和两个由 m 个整数组成的数组 l 和 r,后两个数组表示 m 组范围查询,其中第 i 个查询对应范围 [l[i], r[i]] 。所有数组的下标都是 从 0 开始 的。
返回 boolean 元素构成的答案列表 answer 。如果子数组 nums[l[i]], nums[l[i]+1], ... , nums[r[i]] 可以 重新排列 形成 等差数列 ,answer[i] 的值就是 true;否则answer[i] 的值就是 false 。
示例 1:
输入:nums =[4,6,5,9,3,7], l =[0,0,2], r =[2,3,5]输出:[true,false,true]解释: 第 0 个查询,对应子数组 [4,6,5] 。可以重新排列为等差数列 [6,5,4] 。 第 1 个查询,对应子数组 [4,6,5,9] 。无法重新排列形成等差数列。 第 2 个查询,对应子数组[5,9,3,7] 。可以重新排列为等差数列[3,5,7,9] 。
示例 2:
输入:nums = [-12,-9,-3,-12,-6,15,20,-25,-20,-15,-10], l = [0,1,6,4,8,7], r = [4,4,9,7,9,10] 输出:[false,true,false,false,true,true]
提示:
n == nums.lengthm == l.lengthm == r.length2 <= n <= 5001 <= m <= 5000 <= l[i] < r[i] < n-10^5 <= nums[i] <= 10^5
思路:这道题很容易想到的思路就是我们对于每一个查询,对[L,R]区间内的数进行排序,然后判断每一对相邻的数的差值是不是都是一样的。这样总的复杂度为O(m*nlgn)。然而每次拷贝数据的代价是很高昂的,一个容易想到的优化思路是,如果存在两个查询之间存在包含关系或重叠部分,是可以为下一次的排序进行加速:
包含关系:如两个查询[1,10],[3,7],我们先查询[3,7],并对[3,7]之间的数进行排序,判断差分。到下一次查询[1,10]时,我们可以通过二分查找的方式将[1,2],[8,10]这两个区间上的数以有序的方式插进[3,7]。
重叠部分:如两个查询[3,7],[5,9],我们可以拆成[3,5],[5,9],可知这两部分都满足有序,此时可以用归并。
然而这样做编码复杂度会非常高,同时也无法加速无重叠 、无包含的查询。
我们从等差数列本身的性质入手,等差数列满足每一个相邻数对的查都是公差d。设有一个长度为n的等差数列,最大值为max_num,最小值为min_num,那么公差可以按照如下方式求解:
当我们有了公差之后,我们可以反推出这个数列内所有的数
因此本题的思路可以转换为,对每一个查询[L,R],算出公差d,并判断区间内每一个数是否满足下式且只出现一次(值得注意的是,如果公差为d即最大值等于最小值则一定是等差数列)。
class Solution {
public:vector<bool> checkArithmeticSubarrays(vector<int>& nums, vector<int>& l, vector<int>& r) {int n = nums.size(), min_num[n + 5][n + 5], max_num[n + 5][n + 5], L, R, t, idx, len, d, tempIdx, diff, min_value, max_value;const int maxn = 2e5 +7;bool existItemIdx[maxn];vector<bool> isArithmetic;for(len = 1; len <= n; ++ len){for(L = 0; L + len <= n; ++ L){if(len == 1){min_num[L][L] = max_num[L][L] = nums[L];}else{R = L + len - 1;t = L + (len >> 1) -1;min_num[L][R] = min(min_num[L][t], min_num[t + 1][R]);max_num[L][R] = max(max_num[L][t], max_num[t + 1][R]);}}}for(idx = 0; idx < l.size(); ++ idx){L = l[idx];R = r[idx];min_value = min_num[L][R];max_value = max_num[L][R];if(R - L <= 1 || max_value == min_value){//长度小于等于2或者最大最小值相等即公差为0isArithmetic.push_back(true);}else{d = (max_value - min_value) / (R - L);if(d * (R - L) == max_value - min_value){memset(existItemIdx, false, sizeof(existItemIdx));for(tempIdx = L; tempIdx <= R; ++ tempIdx){\diff = nums[tempIdx] - min_value;if(diff % d != 0 || existItemIdx[diff / d]){isArithmetic.push_back(false);break;}else{existItemIdx[diff / d] = true;}if(tempIdx == R){isArithmetic.push_back(true);}}}else{isArithmetic.push_back(false);}}}return isArithmetic;}
};上述使用区间dp来求取区间最大、最小值有点大材小用了,也可以用对每一个查询遍历的方式。
class Solution {
public:vector<bool> checkArithmeticSubarrays(vector<int>& nums, vector<int>& l, vector<int>& r) {int n = nums.size(), L, R, t, idx, len, d, tempIdx, diff, min_value, max_value;const int maxn = 2e5 +7;bool existItemIdx[maxn];vector<bool> isArithmetic;for(idx = 0; idx < l.size(); ++ idx){L = l[idx];R = r[idx];min_value = max_value = nums[L];for(tempIdx = L + 1; tempIdx <= R; ++ tempIdx){min_value = min(min_value, nums[tempIdx]);max_value = max(max_value, nums[tempIdx]);}if(R - L <= 1 || max_value == min_value){//长度小于等于2或者最大最小值相等即公差为0isArithmetic.push_back(true);}else{d = (max_value - min_value) / (R - L);if(d * (R - L) == max_value - min_value){memset(existItemIdx, false, sizeof(existItemIdx));for(tempIdx = L; tempIdx <= R; ++ tempIdx){\diff = nums[tempIdx] - min_value;if(diff % d != 0 || existItemIdx[diff / d]){isArithmetic.push_back(false);break;}else{existItemIdx[diff / d] = true;}if(tempIdx == R){isArithmetic.push_back(true);}}}else{isArithmetic.push_back(false);}}}return isArithmetic;}
};相关文章:
1630.等差子数组
1630. 等差子数组 难度中等 如果一个数列由至少两个元素组成,且每两个连续元素之间的差值都相同,那么这个序列就是 等差数列 。更正式地,数列 s 是等差数列,只需要满足:对于每个有效的 i , s[i1] - s[i] …...
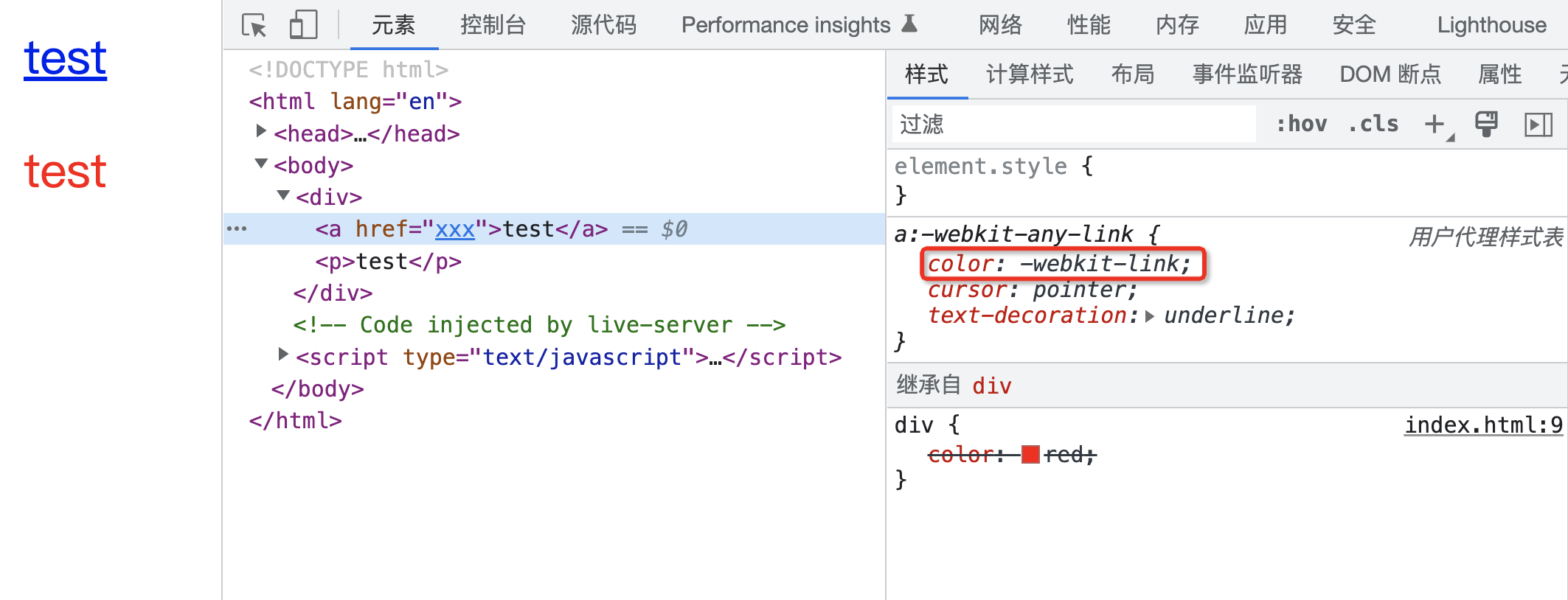
CSS 属性计算过程
CSS 属性计算过程 你是否了解 CSS 的属性计算过程呢? 有的同学可能会讲,CSS属性我倒是知道,例如: p{color : red; }上面的 CSS 代码中,p 是元素选择器,color 就是其中的一个 CSS 属性。 但是要说 CSS 属…...

ThinkPHP02:路由
ThinkPHP02:路由一、路由定义二、变量规则三、路由地址四、路由参数五、路由分组六、MISS七、资源路由八、注解路由九、URL生成一、路由定义 路由默认开启,在 config/app.php 中可以关闭路由。 路由配置在 config/route.php 中,路由定义在 r…...

制作简单进销存管理系统(C#)
实验三:制作简单进销存管理系统 任务要求: 在进销存管理系统中,商品的库存信息有很多种类,比如商品型号、商品名称、商品库存量等。在面向对象编程中,这些商品的信息可以存储到属性中,然后当需要使用这些…...
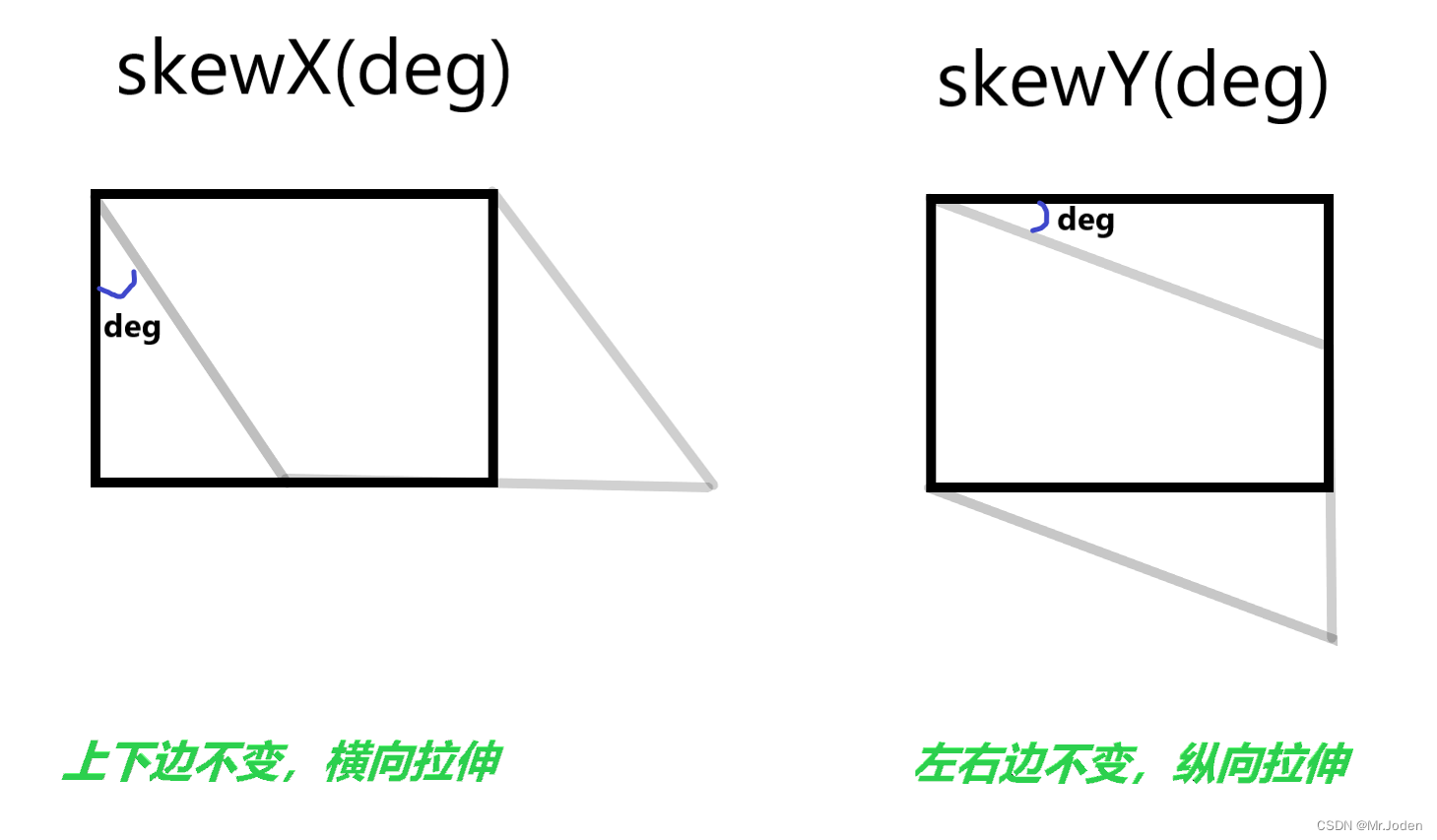
css总结9(过渡和2D变换)
目录 过渡 2D变换 3D变换 过渡 属性结构图 过渡补充 ### 过渡多个元素样式属性 transition:style1 duration , style2 duration,...; ### 过渡所有属性 transition: all duration; 简单示例 ### 移入时改变长度且加入过渡效果 div { width:100px; height:100px; …...
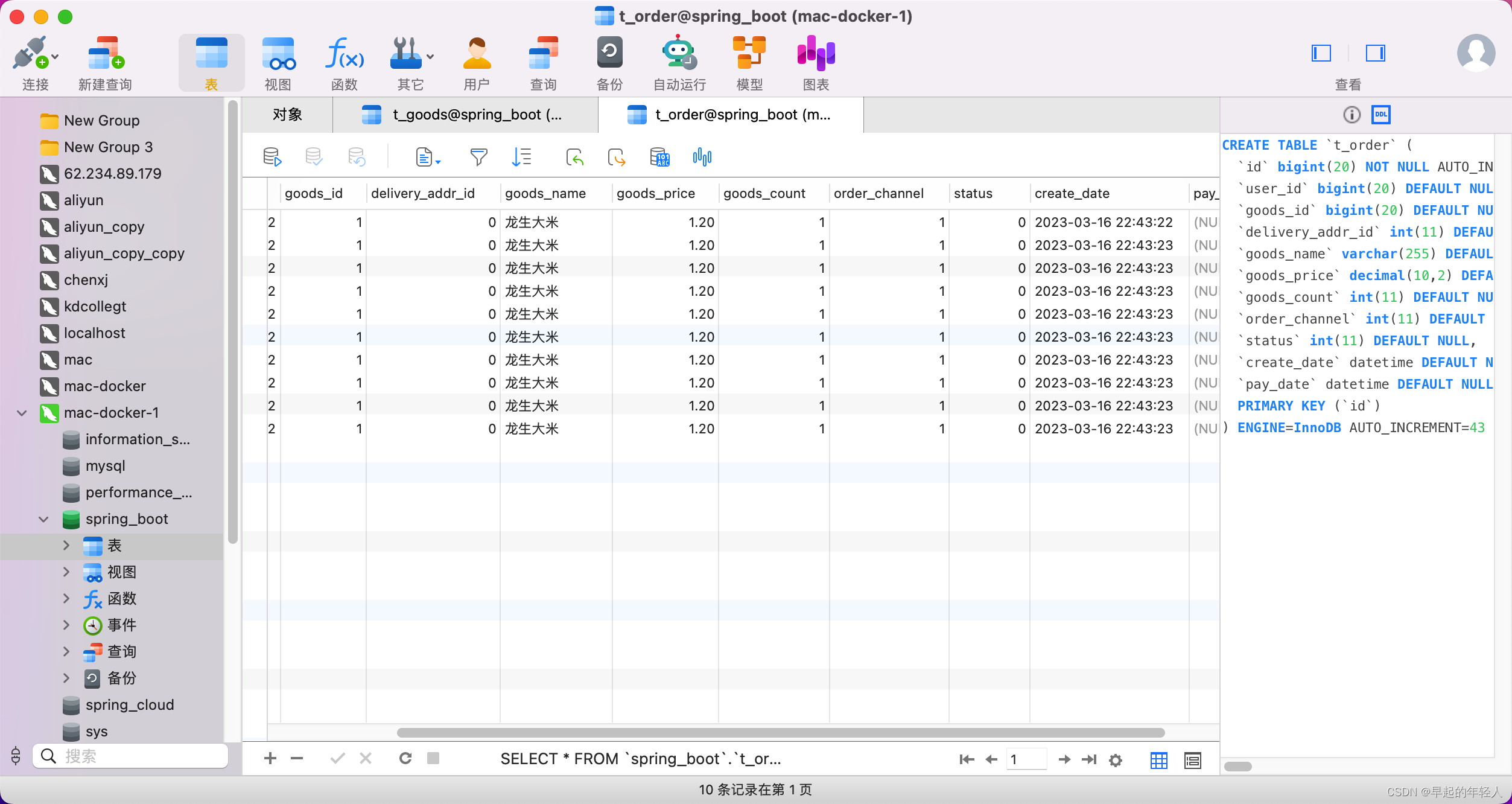
SpringBoot 结合RabbitMQ与Redis实现商品的并发下单【SpringBoot系列12】
SpringCloud 大型系列课程正在制作中,欢迎大家关注与提意见。 程序员每天的CV 与 板砖,也要知其所以然,本系列课程可以帮助初学者学习 SpringBooot 项目开发 与 SpringCloud 微服务系列项目开发 1 项目准备 SpringBoot 整合 RabbitMQ 消息队…...

【python进阶】序列切片还能这么用?切片的强大比你了解的多太多
📚引言 🙋♂️作者简介:生鱼同学,大数据科学与技术专业硕士在读👨🎓,曾获得华为杯数学建模国家二等奖🏆,MathorCup 数学建模竞赛国家二等奖🏅,…...
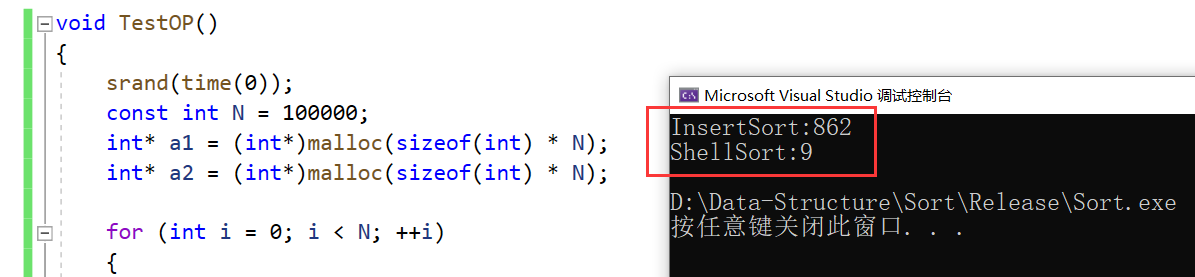
[数据结构]直接插入排序、希尔排序
文章目录排序的概念和运用排序的概念排序运用常见的排序算法常见的排序算法直接插入排序希尔排序性能对比排序的概念和运用 排序的概念 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操…...

CNN、LeNet、AlexNet、VGG、GoogLeNet、RCNN、Fast RCNN、Faster RCNN、YOLO、YOLOv2、SSD等的关系
卷积神经网络的现状1943年美国数学家提出人工智能1949年心理学家建立神经元模型1957年弗兰克提出 感知器人工神经网络模型1980年建立多层感知器模型1984日本学者提出卷积神经网络原始模型神经感知机1998年提出LeNet-5卷积神经网络,并发展了其在音符和字符上的优势20…...
)
IO-day1-(fscanf、fprintf.........)
作业一、有一个usr.txt的文件,其中存储着用户的账户和密码,格式如下:zhangsan aaaalisi bbbbb空格前面是账户,空格后面是密码,一行一个账户、密码要求如下:从终端获取一个账户名和密码判断是否能够登录成功…...
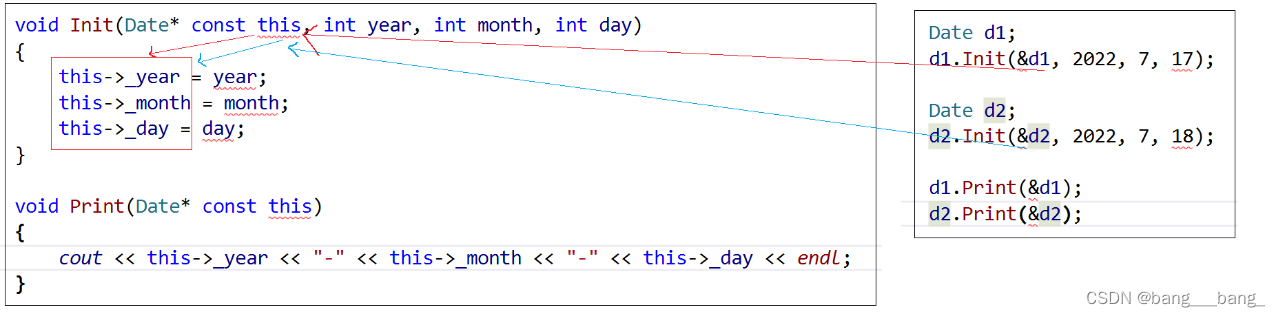
C++类和对象(上篇)
目录 1.类的定义 2.类的访问限定符及封装 2.1类的访问限定符 2.2封装 3.类的作用域 4.类的实例化 5.类的大小 6.this 指针 1.类的定义 class className {// 类体:由成员函数和成员变量组成}; // 一定要注意后面的分号 class为定义类的关键字,Clas…...
解决Xshell无法连接Kali Linux 2020.1(2019.3)版本
使用Xshell远程终端工具连接虚拟机的Kali Linux却提示连接不上原因:Kali Linux默认没有打开SSH远程登录,SSH就是一种网络协议,用于加密的远程登录,所以在没有打开SSH协议之前是无法使用Xshell连接Kali Linux的。解决办法ÿ…...
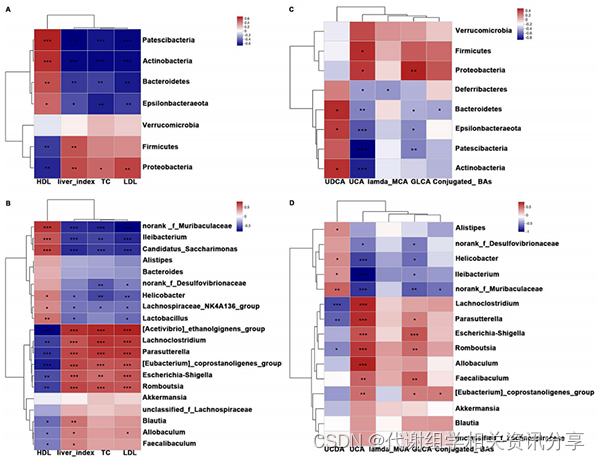
项目文章 | 缓解高胆固醇血症 ,浒苔多糖如何相助?
文章标题:Polysaccharides from Enteromorpha prolifera alleviate hypercholesterolemia via modulating the gut microbiota and bile acid metabolism 发表期刊:Food & Function 影响因子:6.317 作者单位:福建医科大…...
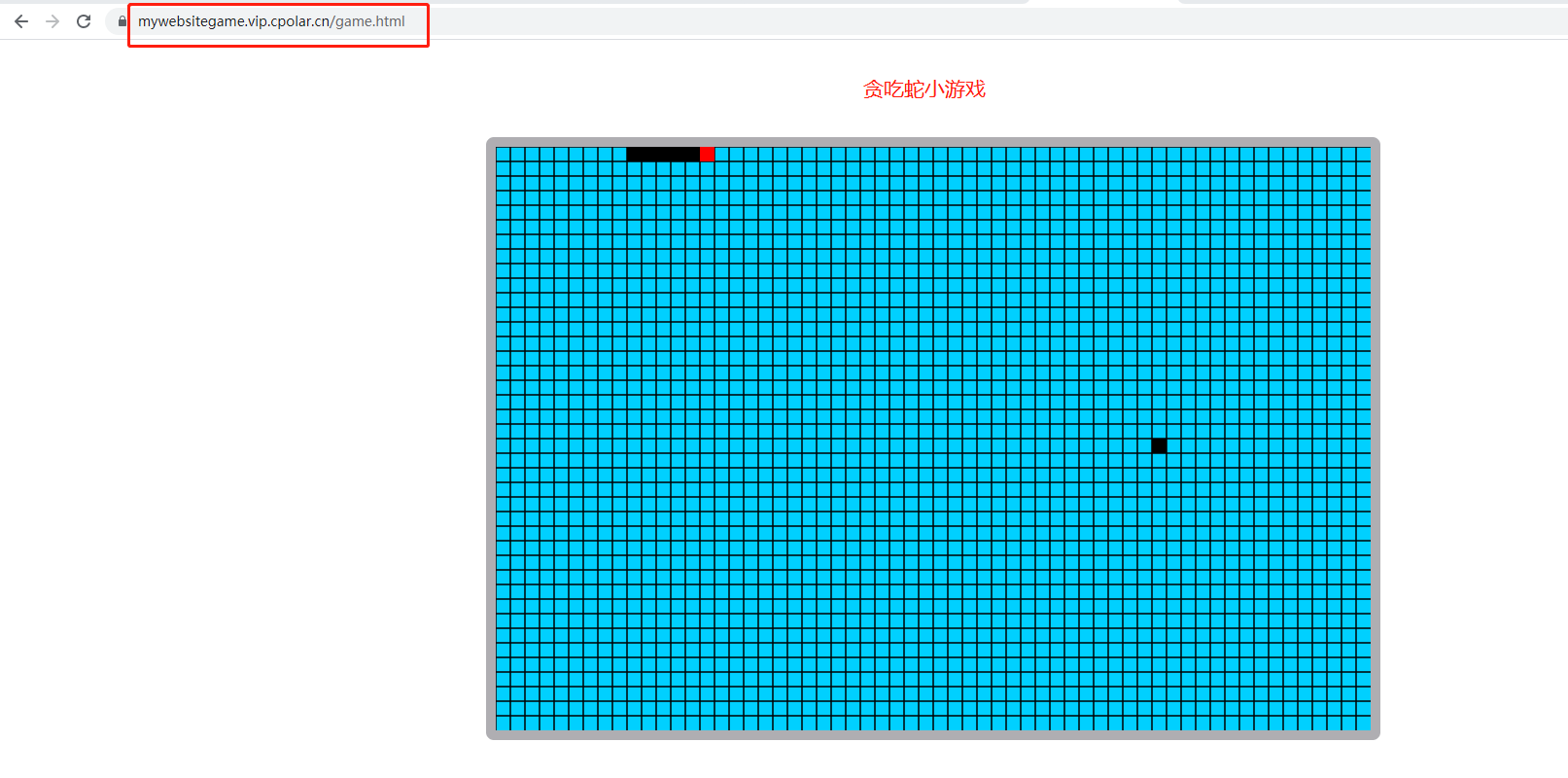
Linux使用宝塔面板搭建网站,并内网穿透实现公网访问
文章目录前言1. 环境安装2. 安装cpolar内网穿透3. 内网穿透4.固定http地址5. 配置二级子域名6.创建一个测试页面前言 宝塔面板作为简单好用的服务器运维管理面板,它支持Linux/Windows系统,我们可用它来一键配置LAMP/LNMP环境、网站、数据库、FTP等&…...
基于深度学习方法与张量方法的图像去噪相关研究
目录 1 研究现状 1.1 基于张量分解的高光谱图像去噪 1.2 基于深度学习的图像去噪算法 1.3 基于深度学习的高光谱去噪 1.4 小结 2 基于深度学习的图像去噪算法 2.1 深度神经网络基本知识 2.2 基于深度学习的图像去噪网络 2.3 稀疏编码 2.3.1 传统稀疏编码 2.3.2 群稀…...
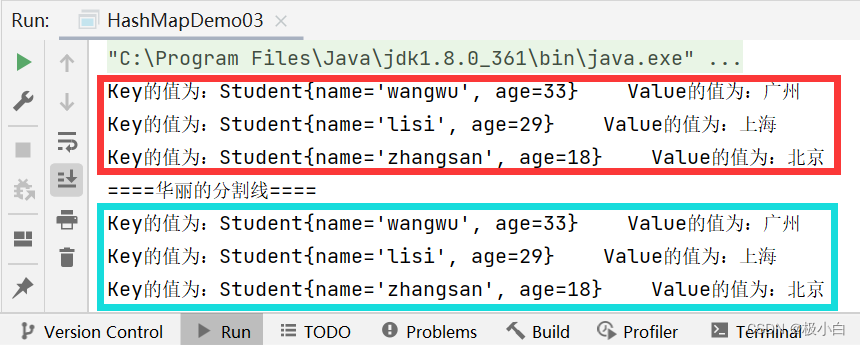
Java基础知识之HashMap的使用
一、HashMap介绍 HashMap是Map接口的一个实现类(HashMap实现了Map的接口),它具有Map的特点。HashMap的底层是哈希表结构。 Map是用于保存具有映射关系的数据集合,它具有双列存储的特点,即一次必须添加两个元素…...

面试--每日一经
操作系统 死锁 死锁:是指两个或两个以上的进程在执行过程中,由于竞争资源或者由于彼此通信而造成的一种阻塞的现象,若无外力作用,它们都将无法推进下去。 死锁的四个必要条件 互斥条件:一个资源每次只能被一个进…...
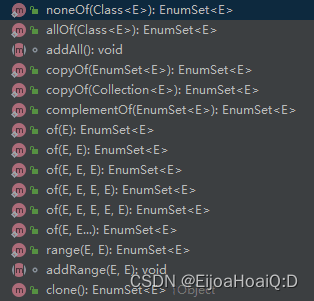
JavaSE进阶之(十六)枚举
十六、枚举16.1 背景16.2 枚举类型16.3 EnumSet 和 EnumMap01、EnumSet02、EnumMap16.1 背景 在 Java 语言中还没有引入枚举类型之前,表示枚举类型的常用模式是声明一组 int 类型的常量,常常用的就是: public static final int SPRING 1; …...

全同态加密:TFHE
参考文献: Cheon J H, Stehl D. Fully homomophic encryption over the integers revisited[C]//Advances in Cryptology–EUROCRYPT 2015: 34th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Sofia, Bulgaria, …...

【计算机二级】综合题目
计算机二级python真题 文章目录计算机二级python真题一、《大学慕课 两问 》二、综合应用题——价值链三、基本操作题 ——信息输出一、《大学慕课 两问 》 附件中的文件data.txt 是教育部爱课程网中国大学MOOC平台的某个 HTML页面源文件,里面包含了我国参与MOOC建设的一批大学…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...
