菜鸟刷题Day1
菜鸟刷题Day1
一.自守数:自守数_牛客题霸_牛客网 (nowcoder.com)
描述
自守数是指一个数的平方的尾数等于该数自身的自然数。例如:25^2 = 625,76^2 = 5776,9376^2 = 87909376。请求出n(包括n)以内的自守数的个数
解题思路:
1.对[0,n]中的每一位数进行平方以后,取平方数的每一位进行判断。但是这样效率有些低,因为每一个数都要取每一位来判断。
#include <stdio.h>
#include <math.h>
int main()
{int n;while(~scanf("%d", &n)) {long count = 0;for (int i = 0; i <= n; i++){long pow_n = pow(i, 2);int tmp = i;while(tmp){if (tmp%10 != pow_n%10) break;tmp/=10;pow_n/=10;} if(tmp == 0)count++;}printf("%d\n", count);}
return 0;
}
2.设一个base=10,如果i==10了,就说明i已经迈入到两位数了,此时base*=10。然后直接接用pow_n%base即可。(也就是说一位数模十,两位数就模100……)
#include<iostream>
#include<math.h>
using namespace std;int main()
{int n=0;int count=0;while(cin>>n)//多组输入{int base=10;for(int i=0;i<=n;i++){long pow_n=pow(i,2);if(i==base)base*=10;if(pow_n%base==i)count++;}cout<<count<<endl; }return 0;
}
二.小于N的质数个数:返回小于 N 的质数个数_牛客题霸_牛客网 (nowcoder.com)
解题思路:
1.编写一个质数判断函数,然后对[2,n]区间内的每一个数都判断一下
2.优化,可以缩小区间,其实只要[2,sqrt(n)]区间内没有n的因数,这个数就肯定是质数
#include<stdio.h>
#include<math.h>int isprime(int num)
{for(int i=0;i<=sqrt(num);i++){if(num%i==0)return 0;}return 1;
}int main()
{int n=0;int count=0;while(scanf("%d",&n)!=EOF){for(int i=2;i<n;i++){if(isprime(i))count++;}printf("%d",count);}return 0;
}
三.第一个只出现一次的字符:第一个只出现一次的字符_牛客题霸_牛客网 (nowcoder.com)
描述
在一个长为 字符串中找到第一个只出现一次的字符,并返回它的位置, 如果没有则返回 -1(需要区分大小写).(从0开始计数)
解题思路
这里给出一个基数排序的思想,既然是字符也就是说最多只有256个数据,建立一个容量为256的字符数组,利用字符的ASCII码值插入到数组的相应位置,然后遍历查找,找到只为1的下标。
int FirstNotRepeatingChar(char* str )
{int len=strlen(str);char arr[256]={0};for(int i=0;i<len;i++){//要判断一下,万一是超长字符可能会溢出if(arr[str[i]]<256){arr[str[i]]+=1;}}//数据录入完毕,查找只数组元素为1的下标for(int j=0;j<len;j++){if(arr[str[j]]==1)return j;}return -1
}
四.判断字符是否唯一:面试题 01.01. 判定字符是否唯一 - 力扣(LeetCode)
描述
实现一个算法,确定一个字符串 s 的所有字符是否全都不同。
解题思路
这一题的思想和上一题一样,只要数组内的所有元素内容都是1,那么就说明所有的字符都是只出现一次。
class Solution
{
public:bool isUnique(string astr) {int len=strlen(astr);char arr[256]={'\0'};for(int i=0;i<len;i++){if(arr[astr[i]]<256){arr[astr[i]]+=1;}}//开始查找判断,是否有出现两次的数据for(int j=0;j<len;j++){if(arr[astr[j]]>1)return false;}return true;}
};
相关文章:

菜鸟刷题Day1
菜鸟刷题Day1 一.自守数:自守数_牛客题霸_牛客网 (nowcoder.com) 描述 自守数是指一个数的平方的尾数等于该数自身的自然数。例如:25^2 625,76^2 5776,9376^2 87909376。请求出n(包括n)以内的自守数的个数 解题思路&#x…...
cjson文件格式介绍
cjson是一种轻量级的JSON解析库,它支持将JSON格式的数据转换为C语言中的数据结构,同时也支持将C语言中的数据结构转换为JSON格式的数据。cjson的文件格式是指在使用cjson库时,将JSON格式的数据存储在文件中,然后通过cjson库读取文…...
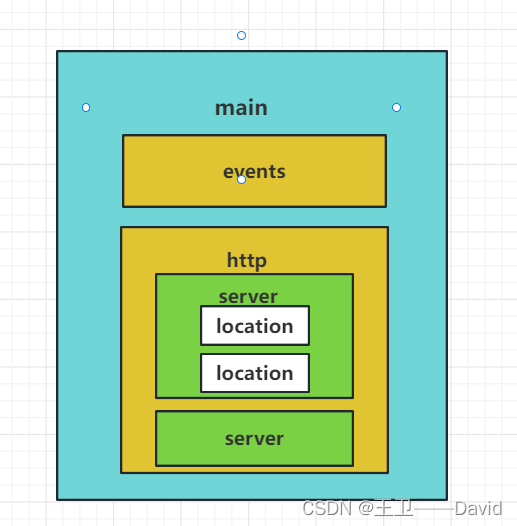
【Nginx二】——Nginx常用命令 配置文件
Nginx常用命令 配置文件常用命令启动和重启 Nginx配置文件maineventshttp常用命令 安装完成nginx后,输入 nginx -?查询nginx命令行参数 nginx version: nginx/1.22.1 Usage: nginx [-?hvVtTq] [-s signal] [-p prefix][-e filename] [-c filename] [-…...
3月最新!AIGC公司生态地图;开发者实用ChatGPT工具清单;上手必会的SD绘图教程;字幕组全自动化流程大公开 | ShowMeAI日报
👀日报&周刊合集 | 🎡生产力工具与行业应用大全 | 🧡 点赞关注评论拜托啦! 🤖 『光年之外诚邀产品经理加入』古典产品经理的复兴! 光年之外创始人王慧文在社交平台发帖,公布联合创始人团队基…...

python - 递归函数
递归函数 什么是递归 在函数内部,可以调用其他函数。如果一个函数在内部调用自身本身,这个函数就是递归函数 递归函数必须有一个明确的结束条件每进入更深一层的递归时,问题规模相对于上一次递归都应减少相邻两次重复之间有紧密的联系&…...

ring_log环形日志-6M缓冲区_proc接口
文章目录log_tools.clog.cspin_lockseq_putsseq_readseq_writesingle_openmakefiletest.sh测试:运行./test.sh读取日志插入日志echo cat测试参考:log_tools.c #include <stdlib.h> #include <stdio.h> #include <sys/types.h> #includ…...

Linux内核进程管理几种CPU调度策略
CPU调度我们知道,程序需要获得CPU的资源才能被调度和执行,那么当一个进程由于某种原因放弃CPU然后进入阻塞状态,下一个获得CPU资源去被调度执行的进程会是谁呢?下图中,进程1因为阻塞放弃CPU资源,此时&#…...
SpringBoot整合Flink(施耐德PLC物联网信息采集)
SpringBoot整合Flink(施耐德PLC物联网信息采集)Linux环境安装kafka前情:施耐德PLC设备(TM200C16R)设置好信息采集程序,连接局域网,SpringBoot订阅MQTT主题,消息转至kafka,…...

DFS(深度优先搜索)和BFS(宽度优先搜索)
目录 DFS(深度优先搜索) 全排列的DFS解法 利用DFS递归构建二进制串和递归树的结构剖析 DFS--剪枝 DFS例题--整数划分 BFS(宽度优先搜索) 全排列的BFS解法 DFS(深度优先搜索) 深度优先搜索(Depth First Search&…...

Redis缓存穿透、击穿、雪崩问题及解决方法
系列文章目录 Spring Cache的使用–快速上手篇 分页查询–Java项目实战篇 全局异常处理–Java实战项目篇 完善登录功能–过滤器的使用 上述只是部分文章,对该系列文章感兴趣的可以查看我的主页哦 文章目录系列文章目录前言一、缓存穿透1.1 问题引入1.2 解决方法1.…...

HAL库 STM32 串口通信
一、实验条件将STM32的PA9复用为串口1的TX,PA10复用为串口1的RX。STM32芯片的输出TX和接收RX与CH340的接收RX和发送TX相连(收发交叉且PCB上默认没有相连,所以需要用P3跳线帽进行手动连接),CH340的另一端通过USB口引出与…...

2023-第十四届蓝桥杯冲刺计划!
💬前言 💡本文以目录形式列举大纲,可根据题目点击跳转 🌈冲刺阶段目的:把握高频重点,结合基础算法和常考题型总结,用真题进行模拟练习 根据自己的能力熟练目前已掌握的算法,不会的还可以暴力 ⏳最后三个星期大家一起冲…...
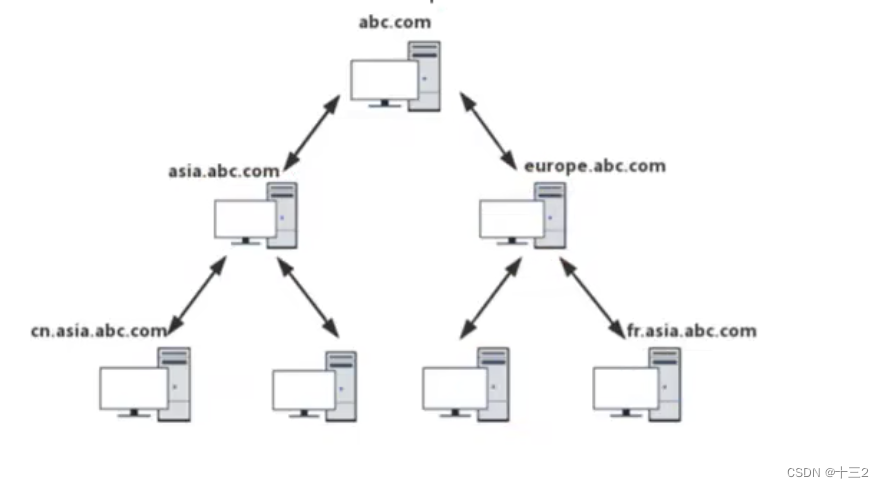
内网渗透基础知识
一、内网概述 内网也指局域网,是指在某一区域内又多台计算机互联成的计算机组。一般是方圆几千米内,局域网可以实现文件管理,应用软件共享,打印机共享,工作组内的历程安排,电子邮件和传真通信服务等功能。…...

鸟哥的Linux私房菜 正则表示法与文件格式化处理
第十一章、正则表示法与文件格式化处理 https://linux.vbird.org/linux_basic/centos7/0330regularex.php 简体版 http://cn.linux.vbird.org/linux_basic/0330regularex.php 11.2.2 grep的一些高级选项 例题一、搜索特定字符串 例题二、利用中括号 [] 来搜寻集合字符 例题四…...
1630.等差子数组
1630. 等差子数组 难度中等 如果一个数列由至少两个元素组成,且每两个连续元素之间的差值都相同,那么这个序列就是 等差数列 。更正式地,数列 s 是等差数列,只需要满足:对于每个有效的 i , s[i1] - s[i] …...
CSS 属性计算过程
CSS 属性计算过程 你是否了解 CSS 的属性计算过程呢? 有的同学可能会讲,CSS属性我倒是知道,例如: p{color : red; }上面的 CSS 代码中,p 是元素选择器,color 就是其中的一个 CSS 属性。 但是要说 CSS 属…...

ThinkPHP02:路由
ThinkPHP02:路由一、路由定义二、变量规则三、路由地址四、路由参数五、路由分组六、MISS七、资源路由八、注解路由九、URL生成一、路由定义 路由默认开启,在 config/app.php 中可以关闭路由。 路由配置在 config/route.php 中,路由定义在 r…...

制作简单进销存管理系统(C#)
实验三:制作简单进销存管理系统 任务要求: 在进销存管理系统中,商品的库存信息有很多种类,比如商品型号、商品名称、商品库存量等。在面向对象编程中,这些商品的信息可以存储到属性中,然后当需要使用这些…...
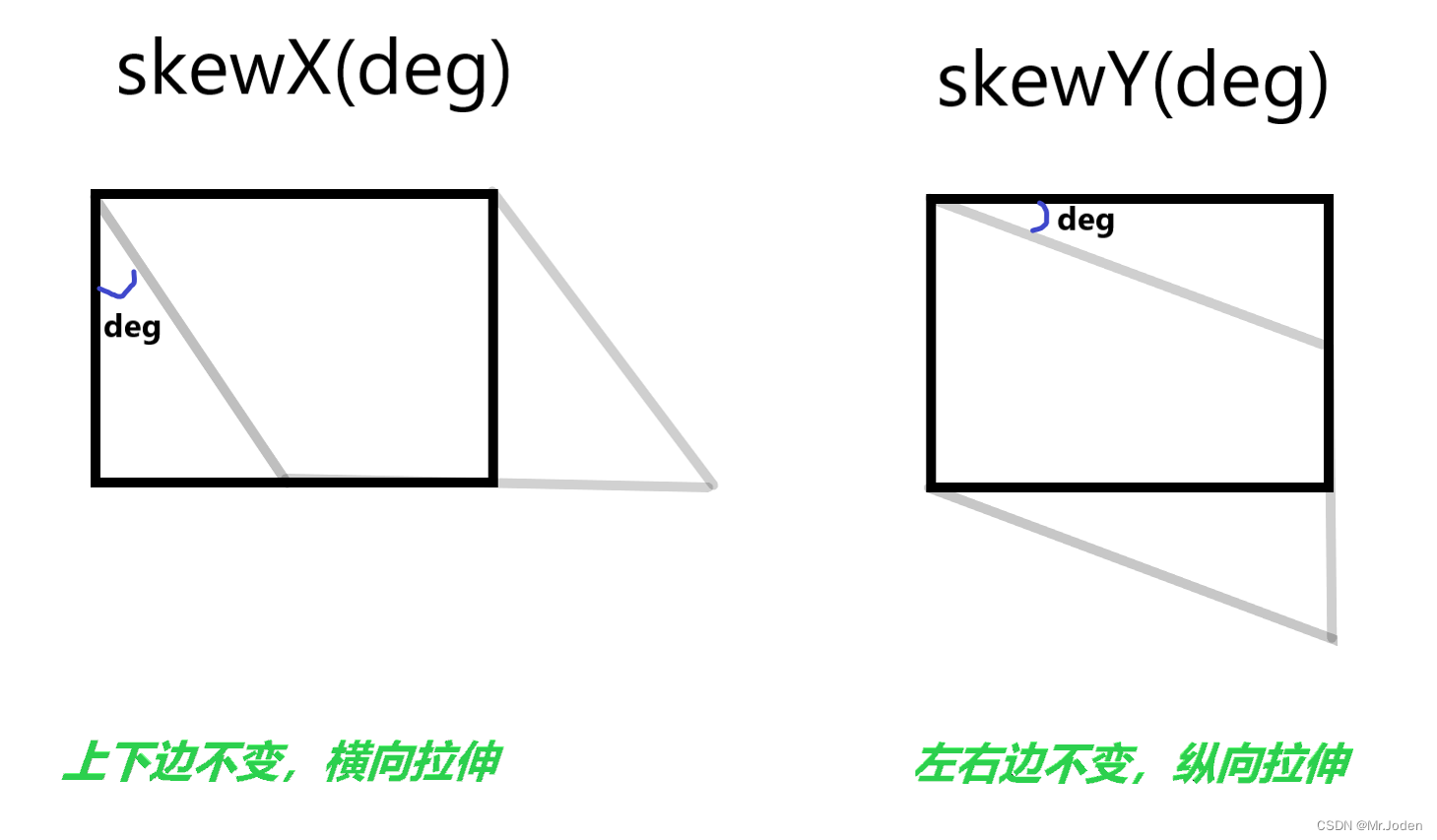
css总结9(过渡和2D变换)
目录 过渡 2D变换 3D变换 过渡 属性结构图 过渡补充 ### 过渡多个元素样式属性 transition:style1 duration , style2 duration,...; ### 过渡所有属性 transition: all duration; 简单示例 ### 移入时改变长度且加入过渡效果 div { width:100px; height:100px; …...
SpringBoot 结合RabbitMQ与Redis实现商品的并发下单【SpringBoot系列12】
SpringCloud 大型系列课程正在制作中,欢迎大家关注与提意见。 程序员每天的CV 与 板砖,也要知其所以然,本系列课程可以帮助初学者学习 SpringBooot 项目开发 与 SpringCloud 微服务系列项目开发 1 项目准备 SpringBoot 整合 RabbitMQ 消息队…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

React父子组件通信:Props怎么用?如何从父组件向子组件传递数据?
系列回顾: 在上一篇《React核心概念:State是什么?》中,我们学习了如何使用useState让一个组件拥有自己的内部数据(State),并通过一个计数器案例,实现了组件的自我更新。这很棒&#…...
