从 X 入门Pytorch——Tensor的自动微分、计算图,常见的with torch.no_grad()机制
这里写目录标题
- 1 Pytorch计算图和自动微分
- 2 将单个数据从计算图中剥离 .detach
- 3 使用with torch.go_grad(): 包含的代码段不会计算微分
1 Pytorch计算图和自动微分
从功能上理解:
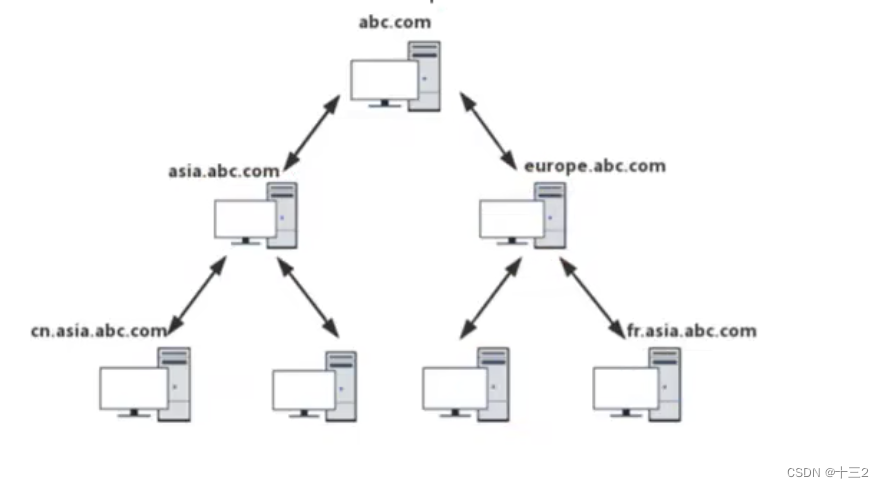
计算图就是类似于数据结构中的无环有向图,Pytorch中的计算图就是为了记录一个数据从开始到最后所作的操作和参数,这样在进行反向传播时候(backward),就会有足够的参数去计算梯度,得到最终值相较于操作过程中数据梯度,之后再通过优化器(optimizer.step()),对目标函数进行优化,就几乎完成了一轮模型训练的目的。
将Tensor的requires_grad属性设置为True时,Pytorch的torch.autograd会自动地追踪它的计算轨迹,当需要计算微分的时候,只需要对最终计算结果的Tensor调用backward方法,中间所有计算节点的微分就会被保存在grad属性中:
import torchx = torch.arange(9, dtype=torch.float).view(3,3)
print("x默认不缓存计算轨迹:",x, x.requires_grad)
y = torch.randn(3,3, requires_grad=True)
print("y设置requires_grad属性:",y, y.requires_grad)
z = torch.sum(torch.mm(x, y))
z.backward()
print("得到Z:", z, z.requires_grad)
print("经过计算,未保留x的梯度:", x.grad)
print("经过计算,保留了y的梯度:", y.grad)out:
x默认不缓存计算轨迹: tensor([[0., 1., 2.],[3., 4., 5.],[6., 7., 8.]]) False
y设置requires_grad属性: tensor([[-0.2810, -2.7142, 1.8053],[-0.6549, 1.0730, -1.9470],[ 0.5629, -0.0692, -0.7376]], requires_grad=True) True
得到Z: tensor(-32.7122, grad_fn=<SumBackward0>) True
经过计算,未保留x的梯度: None
经过计算,保留了y的梯度: tensor([[ 9., 9., 9.],[12., 12., 12.],[15., 15., 15.]])
从上面可以看出,y设置了requires_grad为True时,在计算过后,Pytorch会缓存其梯度信息,而x为设置该属性,即未保存该梯度信息。
汇总:
| Tensor属性 | 作用 |
|---|---|
针对Tensor构造时的属性 | 后期也可以输出查看 |
| device | 该节点运行的设备环境,即CPU/GPU |
| requires_grad | 自动微分机是否需要对该节点求导,缺省为False |
针对Tensor输出时的属性,构造时不可指定 | 用来输出查看 |
| grad | 输出节点对该节点的梯度,缺省为None |
| grad_fn | 中间计算节点关于全体输入节点的映射,记录了前向传播经过的操作。叶节点为None |
| is_leaf | 该节点是否为叶节点 |
当需要计算中间数据(x)的梯度时,只需要将最后的结果值进行backward()后,再打印x.grad即可
2 将单个数据从计算图中剥离 .detach
一般在模型训练中计算评价指标时,我们需要停止数据的计算轨迹缓存,则可以使用.detach将数据从计算图中剥离出去,这个是针对单个数据的。
import torch
x = torch.rand(3, 3, requires_grad=True)
w = torch.ones(3, 3, requires_grad=True)
print(x)
print(w)
yy = torch.mm(w, x)
print(yy.requires_grad)detach_yy = yy.detach() #一般模型中使用loss计算评价指标时,都会用类似这样的式子将loss从计算图中剥离备份出去。
y = torch.sum(yy)
y.backward()print("进行剥离后,detach_yy的属性:", detach_yy.grad)
print("x的梯度缓存:", x.grad)
print("w的梯度缓存:", w.grad)out:
tensor([[0.8037, 0.2443, 0.3994],[0.9879, 0.9484, 0.4035],[0.3057, 0.6682, 0.4186]], requires_grad=True)
tensor([[1., 1., 1.],[1., 1., 1.],[1., 1., 1.]], requires_grad=True)
True
进行剥离后,detach_yy的属性: None
x的梯度缓存: tensor([[3., 3., 3.],[3., 3., 3.],[3., 3., 3.]])
w的梯度缓存: tensor([[1.4474, 2.3398, 1.3925],[1.4474, 2.3398, 1.3925],[1.4474, 2.3398, 1.3925]])
3 使用with torch.go_grad(): 包含的代码段不会计算微分
想必这个在模型测试阶段大家都会用,之所以用这个,是将模型测试阶段的微分不计算在模型中,否则模型把测试集都学过了,那以后拿什么进行模型评价呢?
import torch
x = torch.rand(3, 3, requires_grad=True)
w = torch.ones(3, 3, requires_grad=True)
y = torch.sum(torch.mm(w, x))
print("正常缓存梯度信息:", y.requires_grad)with torch.no_grad():y = torch.sum(torch.mm(w, x))print("在with torch.no_grad中:", y.requires_grad)out:
正常缓存梯度信息: True
在with torch.no_grad中: False
相关文章:
机制)
从 X 入门Pytorch——Tensor的自动微分、计算图,常见的with torch.no_grad()机制
这里写目录标题1 Pytorch计算图和自动微分2 将单个数据从计算图中剥离 .detach3 使用with torch.go_grad(): 包含的代码段不会计算微分1 Pytorch计算图和自动微分 从功能上理解: 计算图就是类似于数据结构中的无环有向图,Pytorch中的计算图就是为了记录…...
三十七、实战演练之接口自动化平台的文件上传
上传文件功能 上传文件功能主要针对需要测试上传文件的接口。原理是,把要测试上传的文件先上传到测试平台,然后把路径写入 用例中,后台真正测试时再将其进行上传。 一、上传文件模型 在testplans/models.py 模块中编写如下模型:…...

菜鸟刷题Day1
菜鸟刷题Day1 一.自守数:自守数_牛客题霸_牛客网 (nowcoder.com) 描述 自守数是指一个数的平方的尾数等于该数自身的自然数。例如:25^2 625,76^2 5776,9376^2 87909376。请求出n(包括n)以内的自守数的个数 解题思路&#x…...
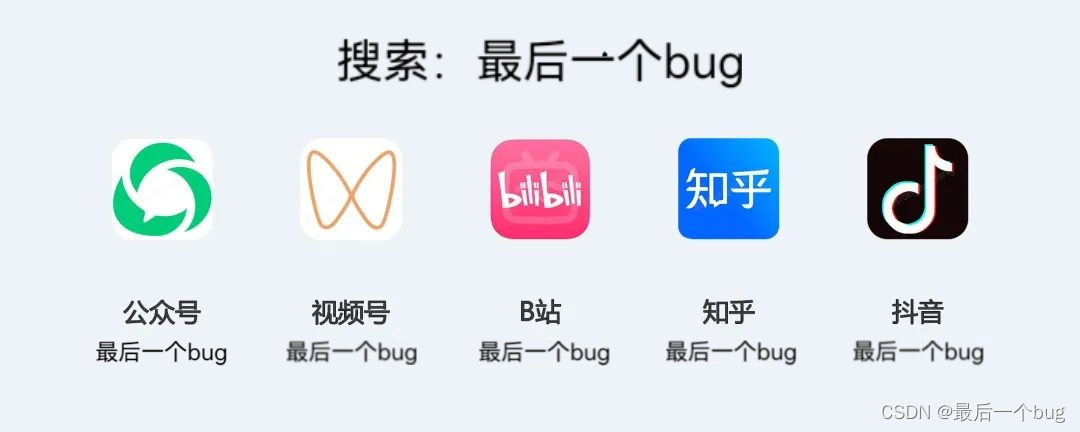
cjson文件格式介绍
cjson是一种轻量级的JSON解析库,它支持将JSON格式的数据转换为C语言中的数据结构,同时也支持将C语言中的数据结构转换为JSON格式的数据。cjson的文件格式是指在使用cjson库时,将JSON格式的数据存储在文件中,然后通过cjson库读取文…...
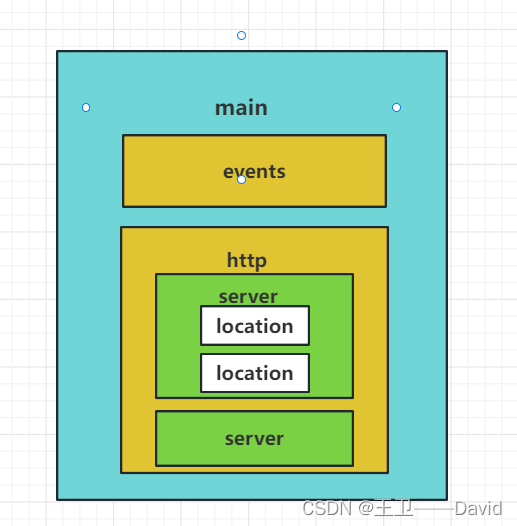
【Nginx二】——Nginx常用命令 配置文件
Nginx常用命令 配置文件常用命令启动和重启 Nginx配置文件maineventshttp常用命令 安装完成nginx后,输入 nginx -?查询nginx命令行参数 nginx version: nginx/1.22.1 Usage: nginx [-?hvVtTq] [-s signal] [-p prefix][-e filename] [-c filename] [-…...
3月最新!AIGC公司生态地图;开发者实用ChatGPT工具清单;上手必会的SD绘图教程;字幕组全自动化流程大公开 | ShowMeAI日报
👀日报&周刊合集 | 🎡生产力工具与行业应用大全 | 🧡 点赞关注评论拜托啦! 🤖 『光年之外诚邀产品经理加入』古典产品经理的复兴! 光年之外创始人王慧文在社交平台发帖,公布联合创始人团队基…...

python - 递归函数
递归函数 什么是递归 在函数内部,可以调用其他函数。如果一个函数在内部调用自身本身,这个函数就是递归函数 递归函数必须有一个明确的结束条件每进入更深一层的递归时,问题规模相对于上一次递归都应减少相邻两次重复之间有紧密的联系&…...

ring_log环形日志-6M缓冲区_proc接口
文章目录log_tools.clog.cspin_lockseq_putsseq_readseq_writesingle_openmakefiletest.sh测试:运行./test.sh读取日志插入日志echo cat测试参考:log_tools.c #include <stdlib.h> #include <stdio.h> #include <sys/types.h> #includ…...

Linux内核进程管理几种CPU调度策略
CPU调度我们知道,程序需要获得CPU的资源才能被调度和执行,那么当一个进程由于某种原因放弃CPU然后进入阻塞状态,下一个获得CPU资源去被调度执行的进程会是谁呢?下图中,进程1因为阻塞放弃CPU资源,此时&#…...
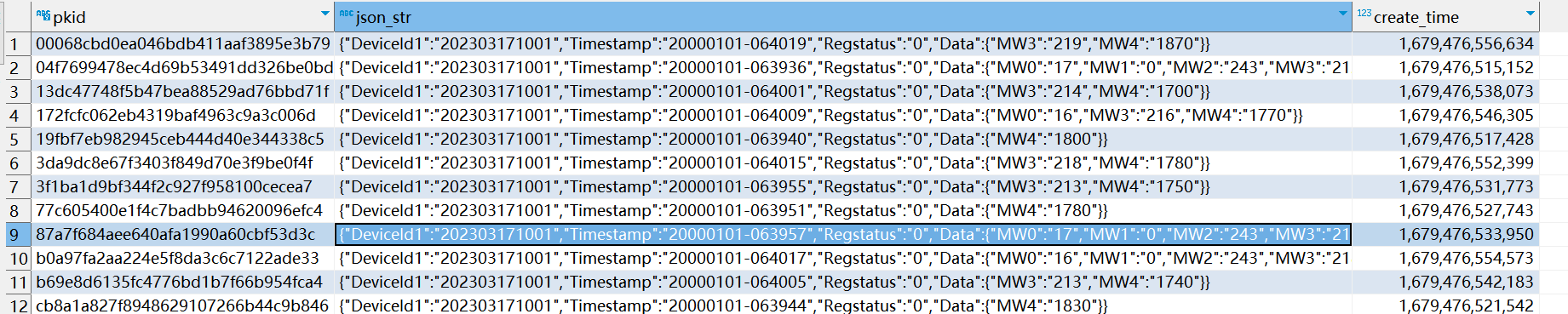
SpringBoot整合Flink(施耐德PLC物联网信息采集)
SpringBoot整合Flink(施耐德PLC物联网信息采集)Linux环境安装kafka前情:施耐德PLC设备(TM200C16R)设置好信息采集程序,连接局域网,SpringBoot订阅MQTT主题,消息转至kafka,…...

DFS(深度优先搜索)和BFS(宽度优先搜索)
目录 DFS(深度优先搜索) 全排列的DFS解法 利用DFS递归构建二进制串和递归树的结构剖析 DFS--剪枝 DFS例题--整数划分 BFS(宽度优先搜索) 全排列的BFS解法 DFS(深度优先搜索) 深度优先搜索(Depth First Search&…...

Redis缓存穿透、击穿、雪崩问题及解决方法
系列文章目录 Spring Cache的使用–快速上手篇 分页查询–Java项目实战篇 全局异常处理–Java实战项目篇 完善登录功能–过滤器的使用 上述只是部分文章,对该系列文章感兴趣的可以查看我的主页哦 文章目录系列文章目录前言一、缓存穿透1.1 问题引入1.2 解决方法1.…...

HAL库 STM32 串口通信
一、实验条件将STM32的PA9复用为串口1的TX,PA10复用为串口1的RX。STM32芯片的输出TX和接收RX与CH340的接收RX和发送TX相连(收发交叉且PCB上默认没有相连,所以需要用P3跳线帽进行手动连接),CH340的另一端通过USB口引出与…...

2023-第十四届蓝桥杯冲刺计划!
💬前言 💡本文以目录形式列举大纲,可根据题目点击跳转 🌈冲刺阶段目的:把握高频重点,结合基础算法和常考题型总结,用真题进行模拟练习 根据自己的能力熟练目前已掌握的算法,不会的还可以暴力 ⏳最后三个星期大家一起冲…...
内网渗透基础知识
一、内网概述 内网也指局域网,是指在某一区域内又多台计算机互联成的计算机组。一般是方圆几千米内,局域网可以实现文件管理,应用软件共享,打印机共享,工作组内的历程安排,电子邮件和传真通信服务等功能。…...

鸟哥的Linux私房菜 正则表示法与文件格式化处理
第十一章、正则表示法与文件格式化处理 https://linux.vbird.org/linux_basic/centos7/0330regularex.php 简体版 http://cn.linux.vbird.org/linux_basic/0330regularex.php 11.2.2 grep的一些高级选项 例题一、搜索特定字符串 例题二、利用中括号 [] 来搜寻集合字符 例题四…...
1630.等差子数组
1630. 等差子数组 难度中等 如果一个数列由至少两个元素组成,且每两个连续元素之间的差值都相同,那么这个序列就是 等差数列 。更正式地,数列 s 是等差数列,只需要满足:对于每个有效的 i , s[i1] - s[i] …...
CSS 属性计算过程
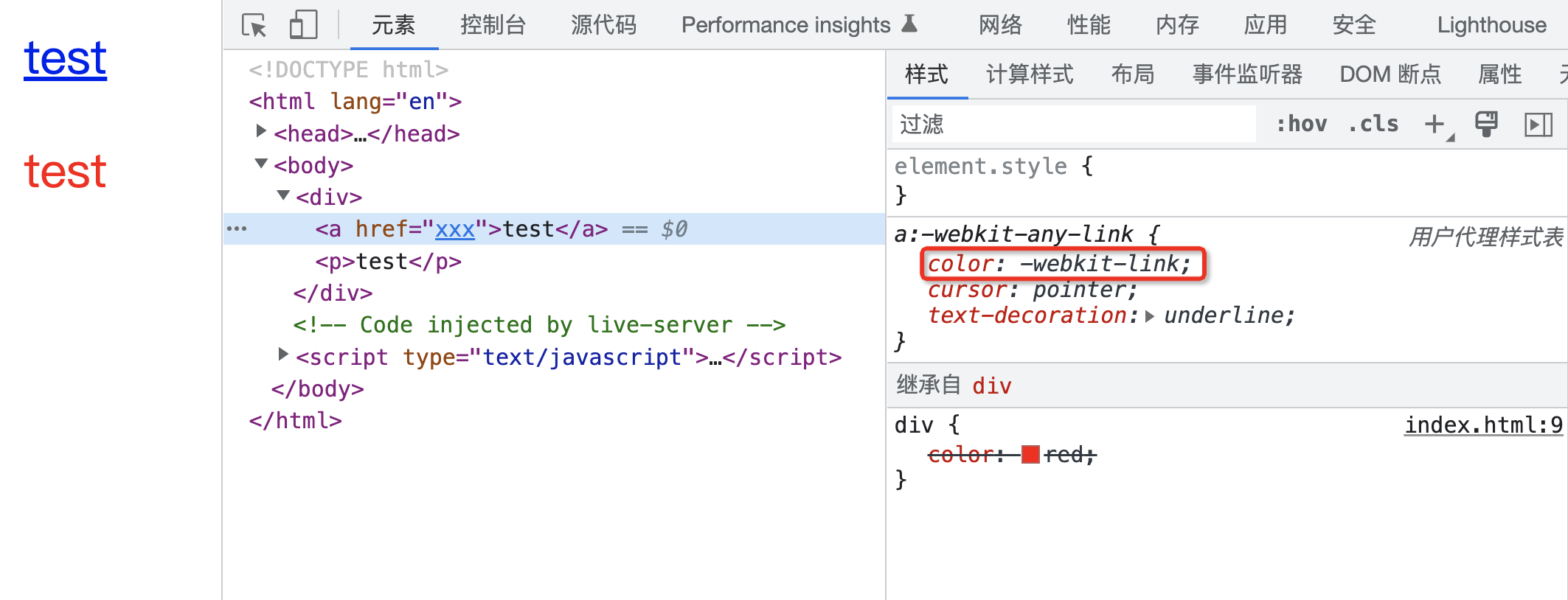
CSS 属性计算过程 你是否了解 CSS 的属性计算过程呢? 有的同学可能会讲,CSS属性我倒是知道,例如: p{color : red; }上面的 CSS 代码中,p 是元素选择器,color 就是其中的一个 CSS 属性。 但是要说 CSS 属…...

ThinkPHP02:路由
ThinkPHP02:路由一、路由定义二、变量规则三、路由地址四、路由参数五、路由分组六、MISS七、资源路由八、注解路由九、URL生成一、路由定义 路由默认开启,在 config/app.php 中可以关闭路由。 路由配置在 config/route.php 中,路由定义在 r…...

制作简单进销存管理系统(C#)
实验三:制作简单进销存管理系统 任务要求: 在进销存管理系统中,商品的库存信息有很多种类,比如商品型号、商品名称、商品库存量等。在面向对象编程中,这些商品的信息可以存储到属性中,然后当需要使用这些…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
