【蓝桥杯-筑基篇】搜索
🍓系列专栏:蓝桥杯
🍉个人主页:个人主页
目录
递归树
1.递归构建二进制串
2.全排列的 DFS 解法
3.全排列的 BFS 解法
4.数的划分法
5.图书推荐
递归树
递归树是一种用于分析递归算法时间复杂度的工具。它可以将递归算法的执行过程可视化,从而更好地理解算法的时间复杂度。
递归树的构造方法如下:
- 首先,将递归算法的输入规模表示为根节点。
- 然后,将递归算法的每一次递归调用表示为树的一个子节点。
- 对于每个子节点,将其表示为一个与父节点相同的问题,但是规模更小的子问题。
- 重复上述步骤,直到递归算法的规模为 1 或者 0。
递归树的叶子节点表示递归算法的基本操作,而递归树的深度表示递归算法的递归深度。通过递归树,可以很容易地计算出递归算法的时间复杂度。
以下是一个递归树的例子:
构建二进制串
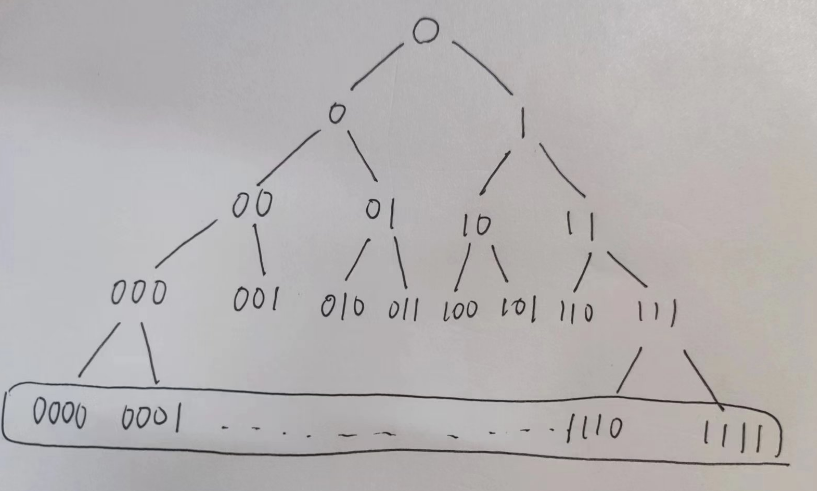
这个递归树表示的是一个将一个大小为 n 的问题分成两个大小为 n/2 的子问题的递归算法。从根节点到叶子节点的路径长度为 O(log n),因此,这个递归算法的时间复杂度为 O(n log n)。在实际应用中,递归树常常用于分析递归。
1.递归构建二进制串
public class A {public static void main(String[] args) {dg(0,"");}private static void dg(int depth, String bin) {if(depth==4) {System.out.println(bin);return ;}dg(depth+1,bin+"0");dg(depth+1,bin+"1");}}0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 修改一下:
public class A {public static void main(String[] args) {DFS(0,"");}private static void DFS(int depth, String bin) {if(depth==4) {System.out.println(bin);return ;}for (int i = 0; i <= 1; i++) {DFS(depth+1,bin+i);}}}优化:用数组存
在这个例子中,我们使用了一个静态数组arr来存储每个深度的值,当深度达到4时,我们输出这个数组。在DFS函数中,我们使用了一个for循环来遍历每个深度的可能性,即0或1,然后将其存储在数组中,并递归调用DFS函数,直到深度达到4。
public class A {public static int[] arr=new int[4];public static void main(String[] args) {DFS(0);}private static void DFS(int depth) {if(depth==4) {System.out.println(Arrays.toString(arr));return ;}for (int i = 0; i <= 1; i++) {arr[depth]=i;DFS(depth+1);}}}结果:
[0, 0, 0, 0] [0, 0, 0, 1] [0, 0, 1, 0] [0, 0, 1, 1]
[0, 1, 0, 0] [0, 1, 0, 1] [0, 1, 1, 0] [0, 1, 1, 1]
[1, 0, 0, 0] [1, 0, 0, 1] [1, 0, 1, 0] [1, 0, 1, 1]
[1, 1, 0, 0] [1, 1, 0, 1] [1, 1, 1, 0] [1, 1, 1, 1] 2.全排列的 DFS 解法
这段代码是一个全排列的DFS解法。我们使用了递归的方式来生成所有可能的排列。初始时,我们调用DFS函数,初始深度为0,初始答案为空字符串,n为3。在DFS函数中,我们首先判断当前深度是否达到n,如果达到,则输出答案并返回。否则,我们遍历所有可能的下一位数,如果该数未被使用,则将其加入到答案中,并递归调用DFS函数,深度加1。当递归返回时,我们将该数从答案中删除,以便遍历其他可能的下一位数。下面是代码实现:
public class A {public static void main(String[] args) {DFS(0,"",3);}private static void DFS(int depth, String ans,int n) {if(depth==n) {System.out.println(ans);return ;}for (int i = 1; i <= n; i++) {if(!ans.contains(""+i))DFS(depth+1,ans+i,n);}}}123 132 213 231 312 321 3.全排列的 BFS 解法
这段代码是一个全排列的BFS解法。我们使用了一个队列来存储每个深度的可能性,初始时,队列中包含了所有可能的第一位数。然后,我们遍历队列中的所有元素,将当前深度的可能性加入到队列中。当深度达到n时,队列中的所有元素即为所有可能的排列。
下面是代码实现:
public class A {public static void main(String[] args) {int n=3;Queue<String> q=new LinkedList<String>();//将所有可能的第一位数加入队列中for (int i = 1; i <= n; i++) q.offer(""+i);while(!q.isEmpty()) {String head=q.poll();for (int i = 1; i <= n; i++) {//如果当前深度的可能性中已经包含了i,则跳过if(head.contains(""+i)) continue;String son=head+i;//如果当前深度为n,则输出当前深度的可能性if(son.length()==n) System.out.println(son);//否则将当前深度的可能性加入到队列中else q.offer(son);}}}}123 132 213 231 312 321 4.数的划分法
问题描述
将整数n分成k份,且每份不能为空,任意两份不能相同(不考虑顺序)。
例如:n=7,k=3,下面三种分法被认为是相同的:
1,1,5;1,5,1;
5,1,1;
问有多少种不同的分法。输入格式
n,k
输出格式
一个整数,即不同的分法
样例输入
7 3
样例输出
4 {四种分法为:1,1,5;1,2,4;1,3,3;2,2,3;}
给定一个正整数n,将其拆分成k个正整数的和,求方案数。这里使用了深度优先搜索的方法,从min开始枚举每个数,递归求解。其中,fanan表示当前的方案,ans表示方案数,cnt表示调用次数。
public class A {public static int cnt;//调用次数public static int ans;//方案数public static void main(String[] args) {int n=7;//给定的正整数int k=3;//将其拆分成k个正整数的和dfs(n,k,1,"");//从1开始枚举每个数System.out.println("方案数:"+ans);//输出方案数System.out.println("调用次数:"+cnt);//输出调用次数}/*** 深度优先搜索* @param n 给定的正整数* @param k 将其拆分成k个正整数的和* @param min 枚举的最小值* @param fanan 当前的方案*/private static void dfs(int n, int k, int min, String fanan) {cnt++;//调用次数加1if(k==1 && min<=n) {//如果k=1且min<=nans++;//方案数加1System.out.println(fanan+n);//输出方案return ;}if(min*k>n) return ; //剪枝for (int i = min; i < n; i++) {//枚举每个数idfs(n-i,k-1,i,fanan+i+"+");//递归搜索}}}
1+1+5
1+2+4
1+3+3
2+2+3
方案数:4
调用次数:15
5.图书推荐
你是否发现,购物、短视频、资讯等平台背后的智能推荐算法,不断分析着你的购物偏好和浏览习惯;价格算法时刻计算调整着你能购买到的商品价位;导航算法、网约车平台算法和无人驾驶汽车算法等等,时刻影响着我们的出行……
无论是否愿意,我们的生活已被算法包围。为了帮助大家全面认知我们当前所身处的世界,消弭技术发展过快带来的困扰与隐忧,《人人都离不开的算法——图解算法应用》一方面从人工智能算法的五大核心应用领域—公共、商业、医疗、工业、金融的典型场景出发,以通俗化、故事化和漫画化的具体事例,深入解读算法是如何在各行各业具体发挥作用和对日常生活的影响;另一方面,将从算法的责任监管和立法治理等角度,阐述算法开发与应用者们应该如何守好伦理底线,让科技向善而行。
《人人都离不开的算法——图解算法应用》脉络清晰,图文并茂,无论你是工作中会接触到算法应用的从业人员,还是对算法应用感到好奇的小白,本书都有助于你打开视野,看到算法在实际应用中的波澜壮阔。

相关文章:

【蓝桥杯-筑基篇】搜索
🍓系列专栏:蓝桥杯 🍉个人主页:个人主页 目录 递归树 1.递归构建二进制串 2.全排列的 DFS 解法 3.全排列的 BFS 解法 4.数的划分法 5.图书推荐 递归树 递归树是一种用于分析递归算法时间复杂度的工具。它可以将递归算法的执行过程可视化…...

week5-质数-最大公约数-快速幂-组合计数-博弈论
蓝桥 等差数列——欧几里得算法质数质数的判定——试除法分解质因数——试除法筛质数——埃氏筛法筛质数——线性筛法质数问题质数距离约数试除法求约数约数个数约数之和最大公约数-欧几里得算法(辗转相除法)扩展欧几里得算法裴蜀定理应用——线性同余方程消灭老鼠Hankson的趣…...
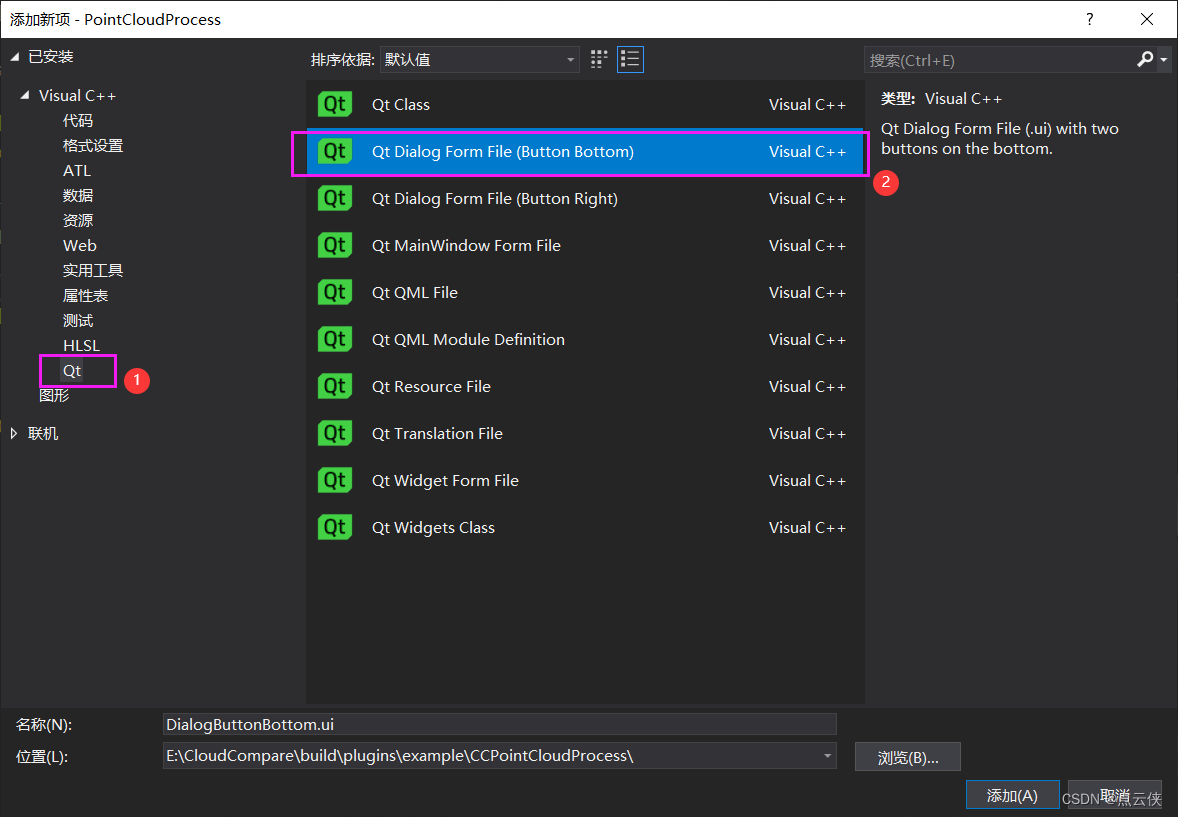
CloudCompare 二次开发(6)——插件中拖拽添加Qt窗口(区域生长算法为例)
目录 一、概述二、插件制作三、Cmake编译四、插件代码五、结果展示一、概述 手动拖拽的方式搭建Qt对话框界面的制作流程,以PCL中的点云区域生长算法为例进行制作。 二、插件制作 1、将....\plugins\example路径下的ExamplePlugin复制一份并修改名字为CCPointCloudProcess。 …...

2023值得推荐的高颜值Vue3.0 Web PC端UI框架,赶紧收藏学习!
Hello,我是前端胡说,本期给大家带来2023值得推荐的Vue3.0 UI组件库,希望大家喜欢! Vue3 正式发布已经有一段时间了,2022年2月也正式变成 Vue 项目的默认版本。在过去一年多的时间里,各大组件库、框架也紧跟…...
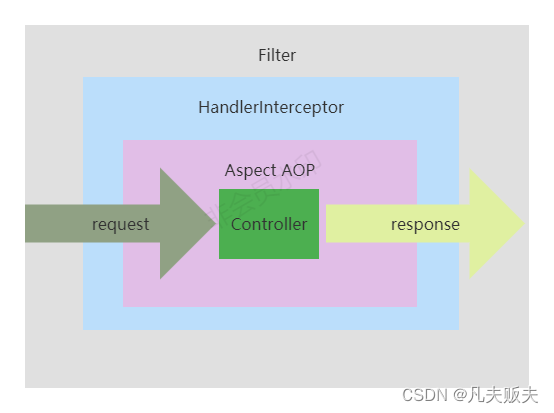
Springboot项目Aop、拦截器、过滤器横向对比
前言伟人曾经说过,没有调查就没有发言权(好像是伟人说的,不管谁说的,这句话是正确的),有些东西看着简单,张口就来,但很有可能是错的。我个人的经验是,aop、过滤器、拦截器的实现方式很简单&…...
为了之后找工作不被虐,每天刷3道《剑指offer》Day-1
本文已收录于专栏🌻《刷题笔记》文章目录前言💖 1、二维数组中的查找题目描述思路💖 2、替换空格题目描述思路💖 3、从尾到头打印链表题目描述思路一(反转函数)思路二(递归)思路二&a…...

Linux-磁盘管理介绍
Linux-磁盘管理介绍 计算硬盘介绍 硬盘是计算机主要存储媒介之一,由一个或者多个铝制或者玻璃制的碟片组成,碟片外覆盖有铁磁性材料,硬盘内部由磁道、柱面、扇区、磁头等部件组成; cylinder:柱面sector:扇区 磁道与…...
爬虫架构(一):爬虫中的去重处理
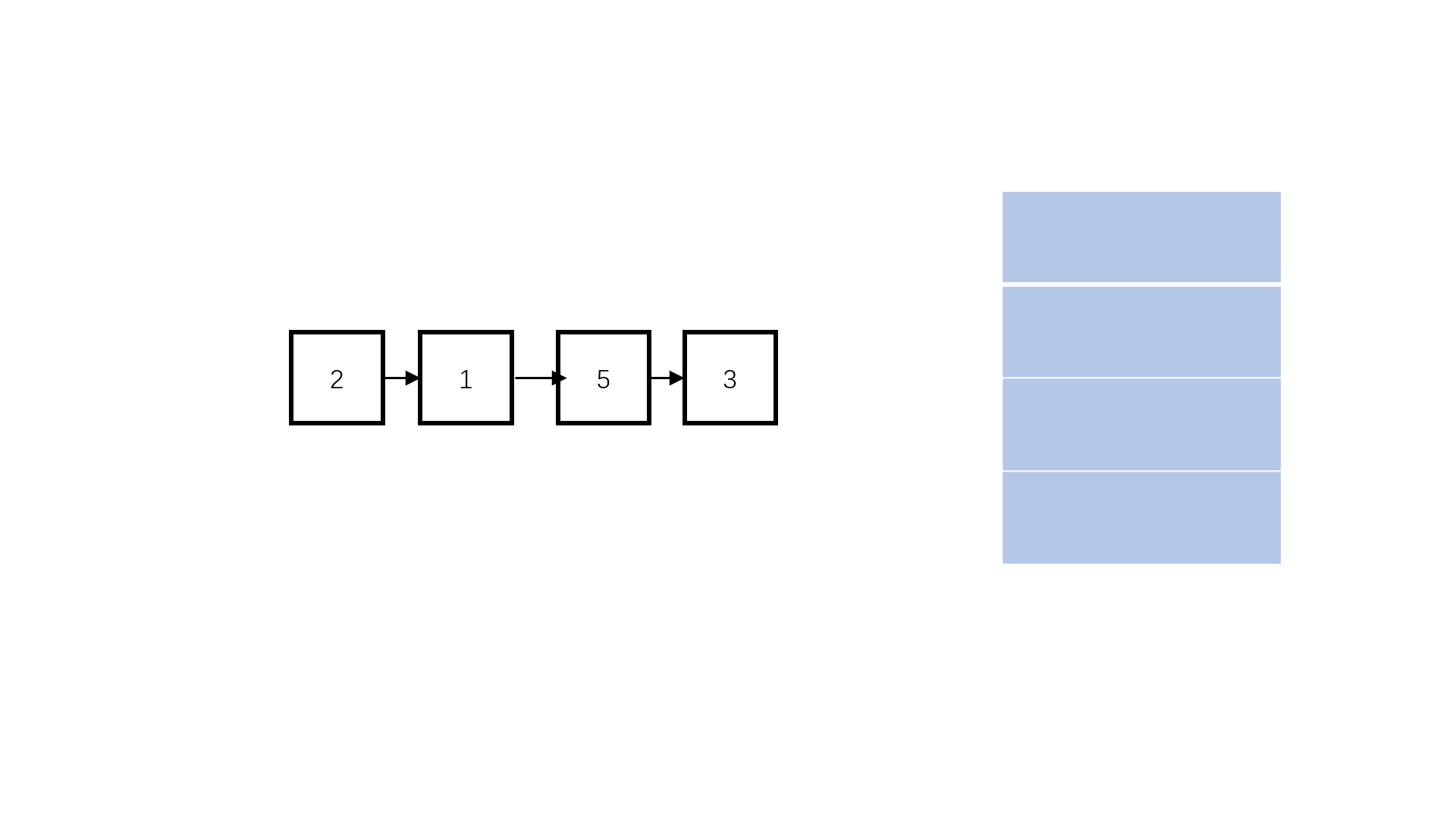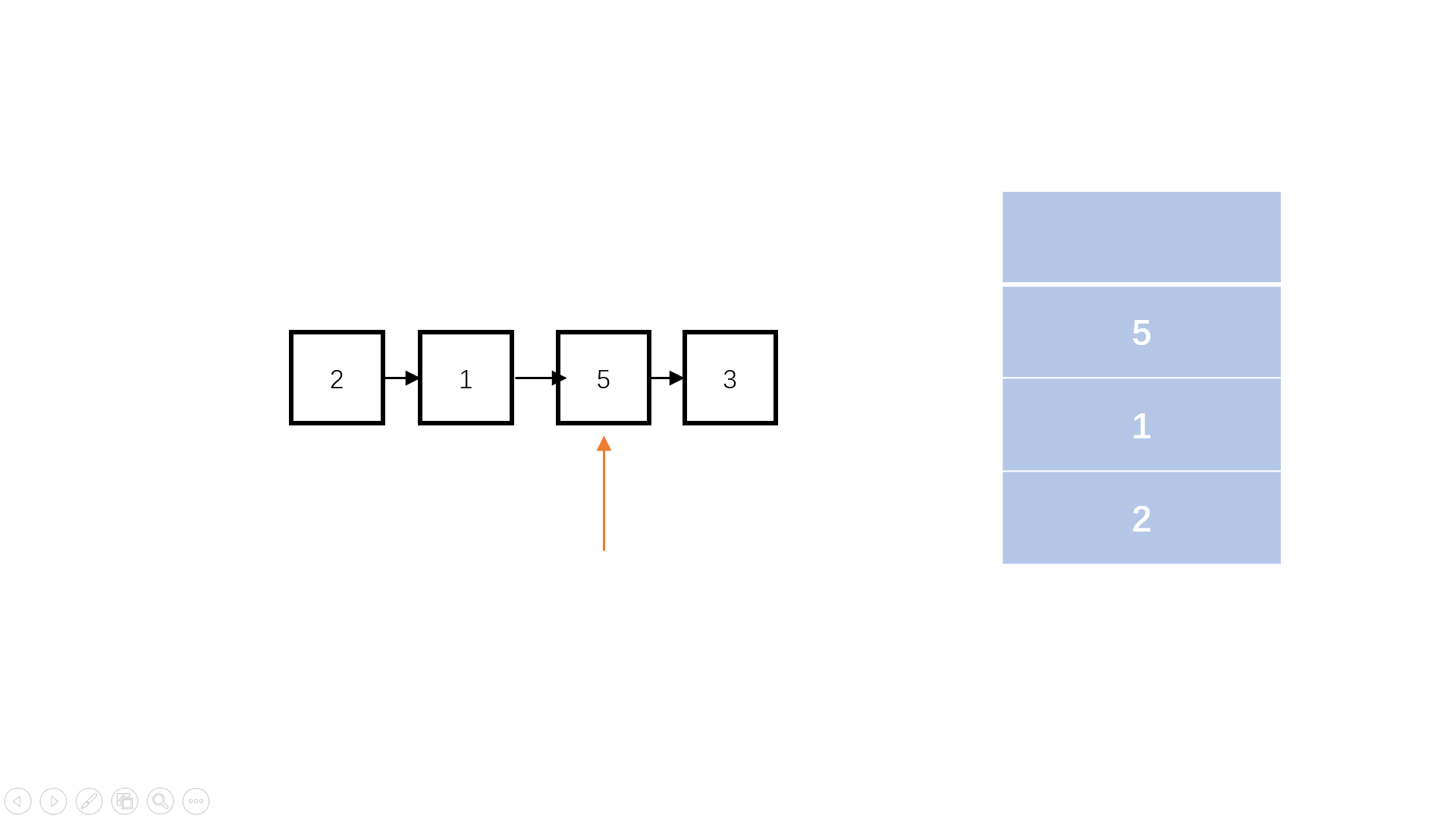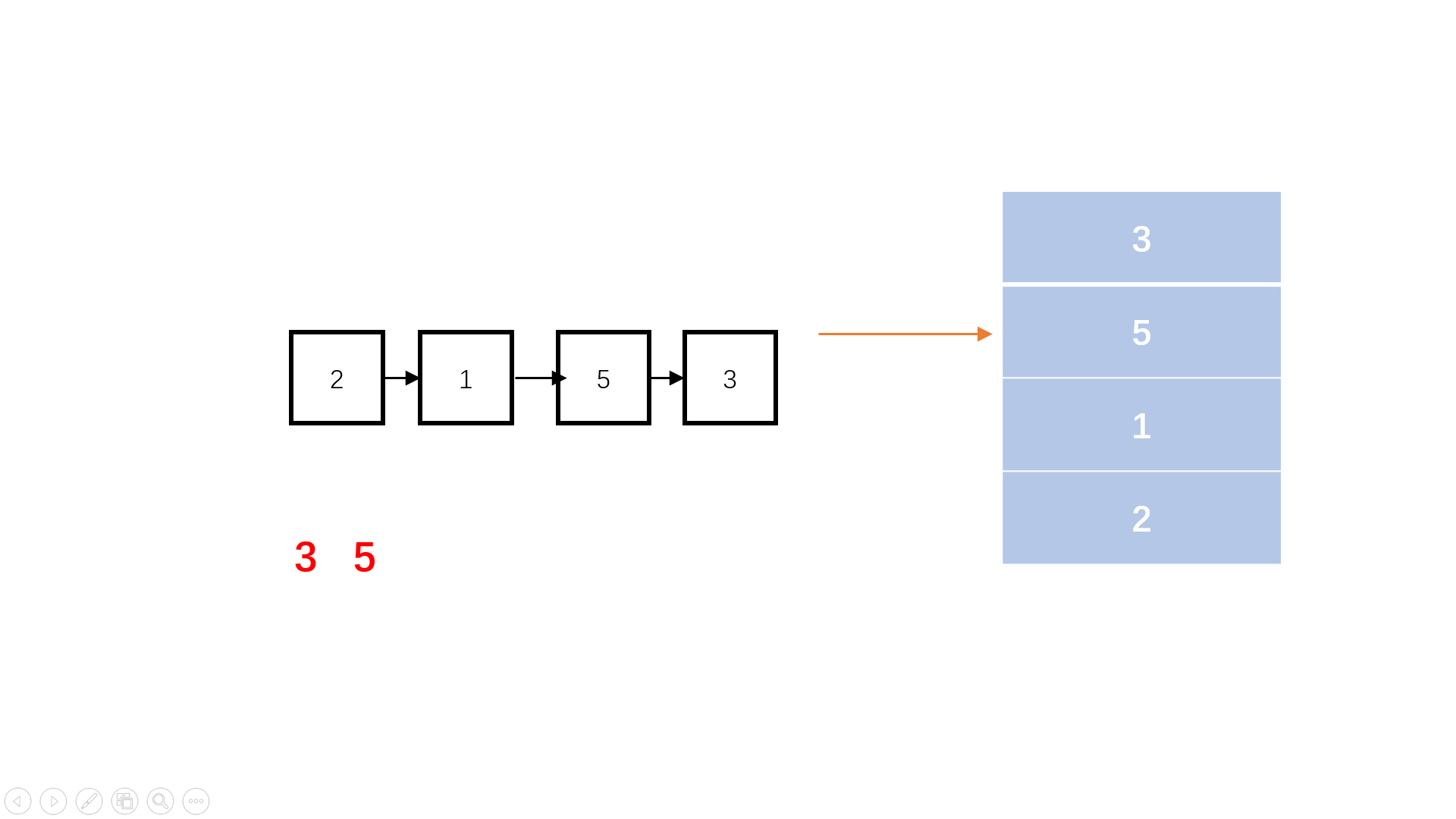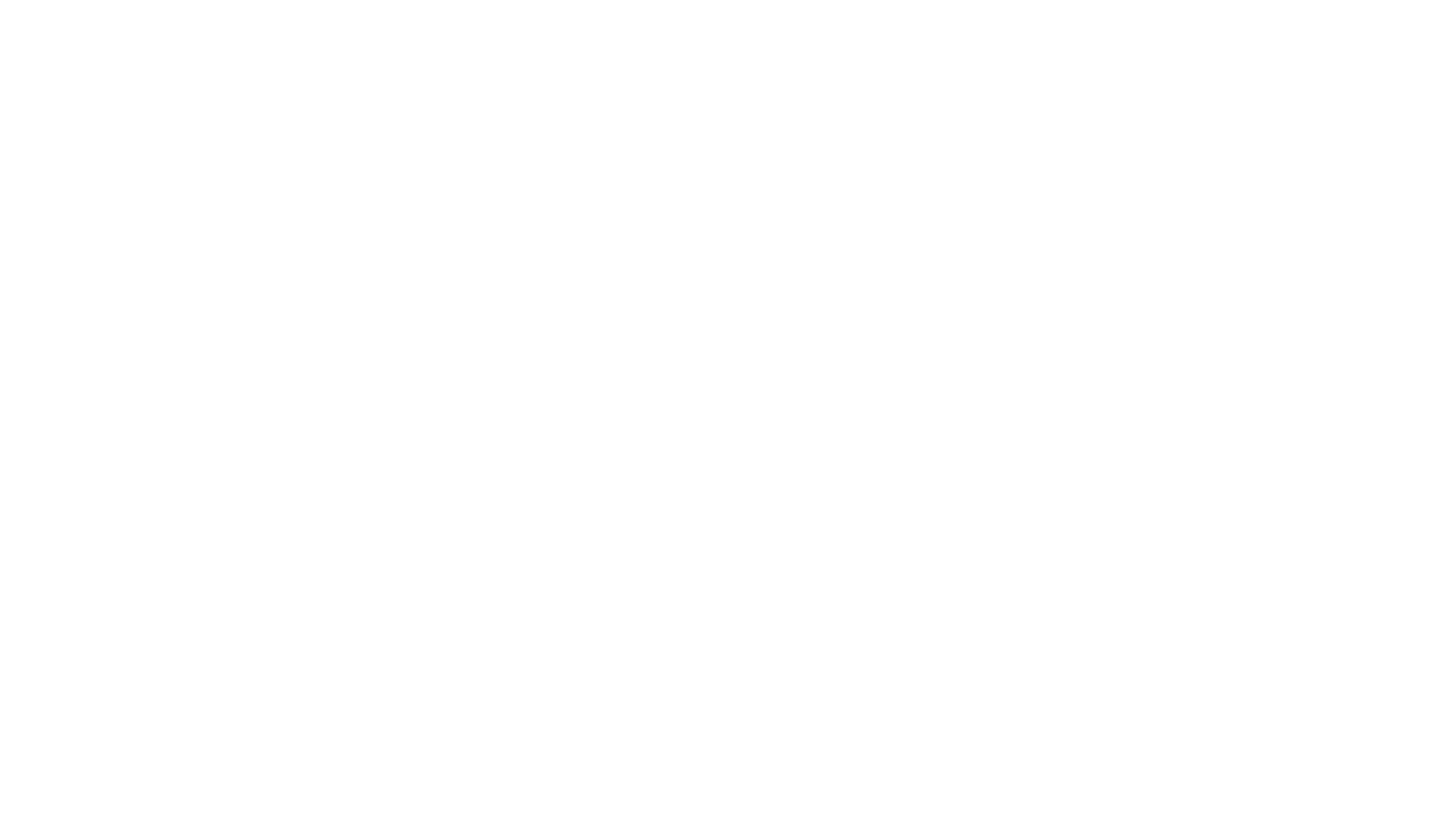
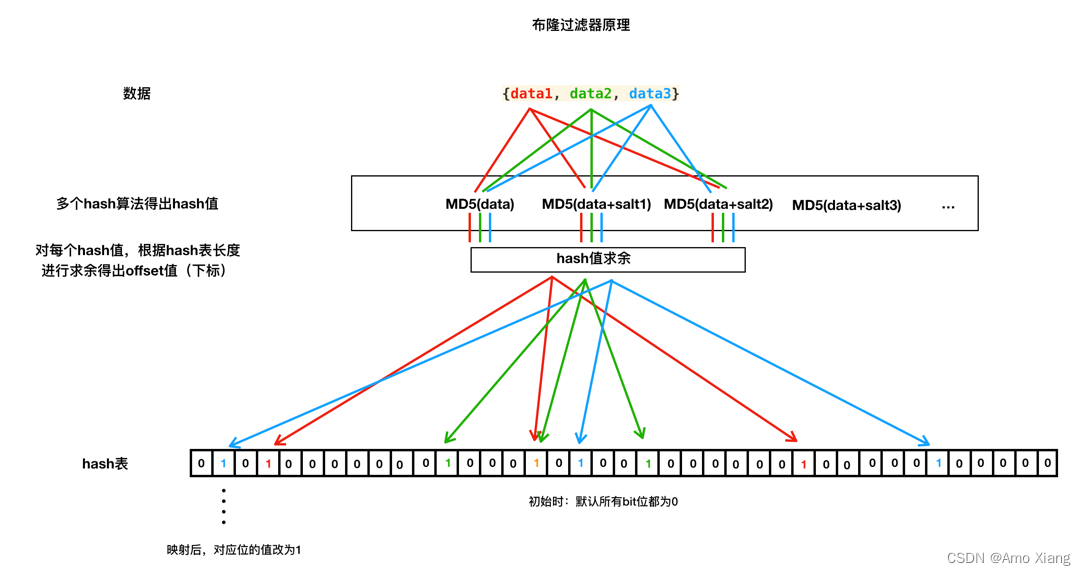
目录一、概要二、去重应用场景以及基本原理2.1 爬虫中什么业务需要使用去重2.2 去重实现的基本原理2.3 根据原始数据进行去重判断2.4 根据原始数据的特征值进行去重判断2.5 临时去重容器与持久化去重容器2.6 常用几种特殊的原始数据特征值计算三、基于信息摘要算法的去重3.1 信…...

算法刷题总结 (二) 回溯与深广搜算法
算法总结2 回溯与深广搜算法一、理解回溯算法1.1、回溯的概念1.2、回溯法的效率1.3、回溯法问题分类1.4、回溯法的做题步骤二、经典问题2.1、组合问题2.1.1、77. 组合 - 值不重复2.1.2、216.组合总和III - 值不重复且等于目标值2.1.3、17. 电话号码的字母组合 - 双层回溯2.1.4、…...

Linux 总结9个最危险的命令,一定要牢记在心!
rm -rf 命令 该命令可能导致不可恢复的系统崩坏。 rm -rf / #强制删除根目录下所有东西。 rm -rf * #强制删除当前目录的所有文件。 rm -rf . #强制删除当前文件夹及其子文件夹。 执行rm -rf 一定要想半天,搞明白自己在干什么. fork 炸弹 😦) { 😐:&am…...
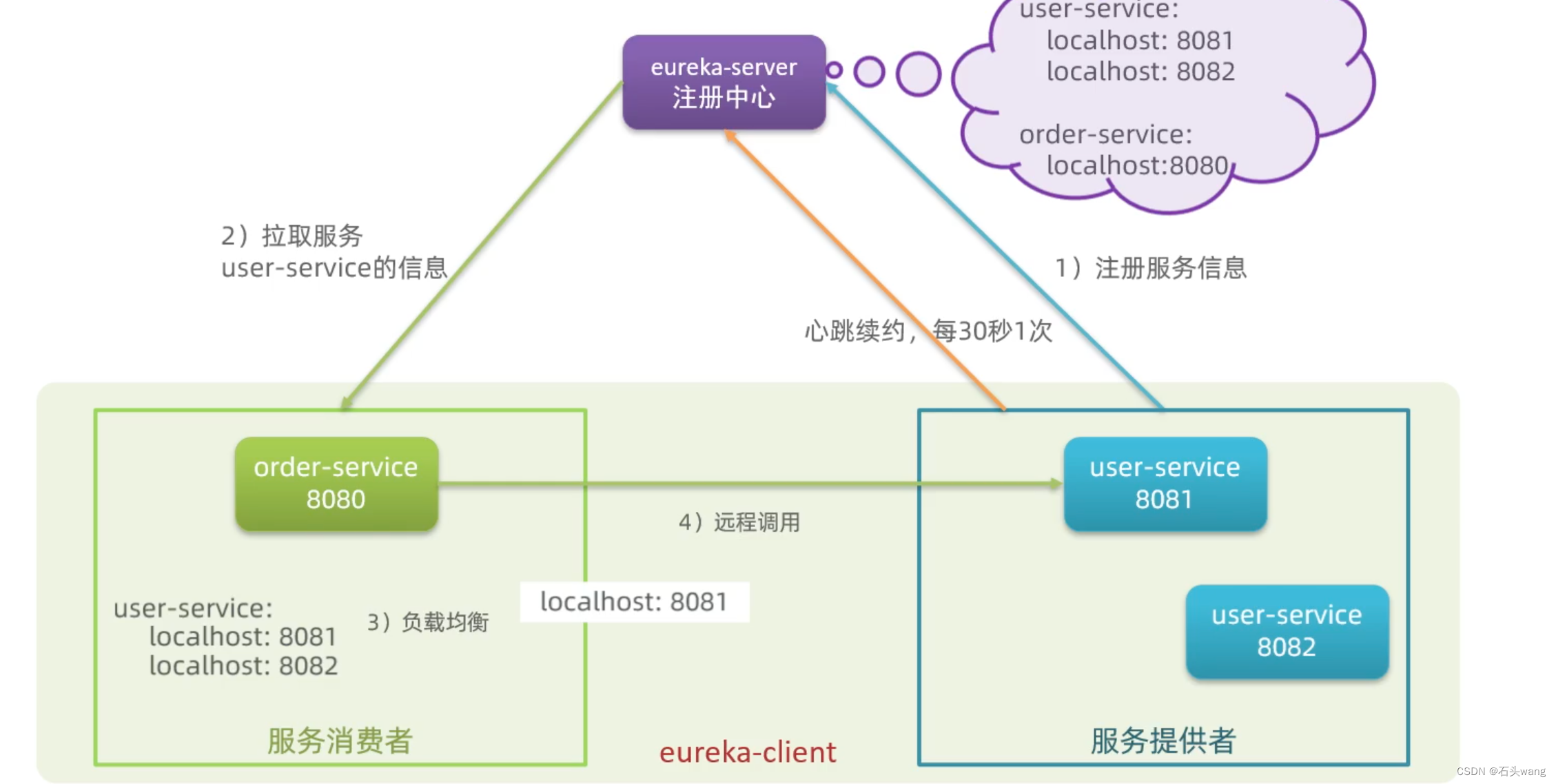
spring cloud
spring cloud 分享 springboot:可以说是spring cloud的基础,是springMVC框架的简化,约定大于配置(在使用上、非功能上的简化) 可以说每个MPO Digital api就是springboot project(springboot项目) spring cloud…...

【9】核心易中期刊推荐——图像视觉与图形可视化
🚀🚀🚀NEW!!!核心易中期刊推荐栏目来啦 ~ 📚🍀 核心期刊在国内的应用范围非常广,核心期刊发表论文是国内很多作者晋升的硬性要求,并且在国内属于顶尖论文发表,具有很高的学术价值。在中文核心目录体系中,权威代表有CSSCI、CSCD和北大核心。其中,中文期刊的数…...

0108Bean销毁-Bean生命周期详解-spring
Bean使用阶段,调用getBean()得到bean之后,根据需要,自行使用。 1 销毁Bean的几种方式 调用org.springframework.beans.factory.support.AbstractAutowireCapableBeanFactory#destroyBean调用org.springframework.beans.factory.config.Conf…...

微信小程序可以进行dom操作吗?
小程序不能使用各种浏览器暴露出来的 DOM API,进行 DOM 选中和操作 原因:在小程序中,渲染层和逻辑层是分开的,分别运行在不同的线程中,逻辑层运行在 JSCore 中,并没有一个完整浏览器对象,因而缺…...

昇腾AI深耕沽上:港口辐射力之后,天津再添基础创新辐射力
作者 | 曾响铃 文 | 响铃说 AI计算正在以新基建联动产业集群的方式,加速落地。 不久前,天津市人工智能计算中心正式揭牌,该中心整体规划300P算力,2022年底首批100P算力上线投入运营,并实现上线即满载。 这是昇腾AI…...
基于YOLOv5的疲劳驾驶检测系统(Python+清新界面+数据集)
摘要:基于YOLOv5的疲劳驾驶检测系统使用深度学习技术检测常见驾驶图片、视频和实时视频中的疲劳行为,识别其闭眼、打哈欠等结果并记录和保存,以防止交通事故发生。本文详细介绍疲劳驾驶检测系统实现原理的同时,给出Python的实现代…...

【Linux】-- 进程优先级和环境变量
目录 进程的优先级 基本概念 如何查看优先级 PRI与NI NI值的设置范围 NI值如何修改 修改方式一 : 通过top指令修改优先级 修改方式二 : 通过renice指令修改优先级 进程的四个重要概念 环境变量 基本概念 常见的环境变量 查看环境变量 三种…...
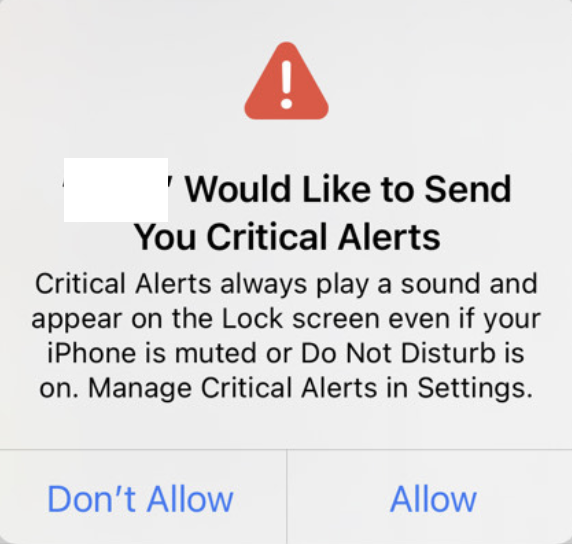
iOS 紧急通知
一般通知 关于通知的各种配置和开发,可以参考推送通知教程:入门 – Kodeco,具有详细步骤。 紧急通知表现 紧急通知不受免打扰模式和静音模式约束。当紧急通知到达时,会有短暂提示音量和抖动(约2s)。未锁…...

即时零售:不可逆的进化
“人们经常问我,这个世界还是平的吗?我经常跟他们说,亲爱的,它真的是平的,比以前更平了。”2021年3月,《世界是平的》作者托马斯弗里德曼在演讲时说。如他所说,尽管逆全球化趋势加剧,…...

零售数据总结经验:找好关键分析指标和维度
各位数据的朋友,大家好,我是老周道数据,和你一起,用常人思维数据分析,通过数据讲故事。 每逢月末、季末、年终,运营部门的同事又要开始进行年终总结分析。那么,对零售连锁企业来说,…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...

【向量库】Weaviate 搜索与索引技术:从基础概念到性能优化
文章目录 零、概述一、搜索技术分类1. 向量搜索:捕捉语义的智能检索2. 关键字搜索:精确匹配的传统方案3. 混合搜索:语义与精确的双重保障 二、向量检索技术分类1. HNSW索引:大规模数据的高效引擎2. Flat索引:小规模数据…...

5. TypeScript 类型缩小
在 TypeScript 中,类型缩小(Narrowing)是指根据特定条件将变量的类型细化为更具体的过程。它帮助开发者编写更精确、更准确的代码,确保变量在运行时只以符合其类型的方式进行处理。 一、instanceof 缩小类型 TypeScript 中的 in…...

SAP学习笔记 - 开发24 - 前端Fiori开发 Filtering(过滤器),Sorting and Grouping(排序和分组)
上一章讲了SAP Fiori开发的表达式绑定,自定义格式化等内容。 SAP学习笔记 - 开发23 - 前端Fiori开发 Expression Binding(表达式绑定),Custom Formatters(自定义格式化)-CSDN博客 本章继续讲SAP Fiori开发…...
