【思维模型】五分钟了解<复利思维>,为何学习复利思维?什么是复利思维?如何应用复利思维?
【思维模型】五分钟了解<复利思维>,为何学习复利思维?什么是复利思维?如何应用复利思维?
- 1. 为何学习复利思维?
- 2. 什么是复利思维?
- 3. 如何应用复利思维?
- 4. 小结
参考:数据化分析、思维模型、林骥
1. 为何学习复利思维?
传说在很久以前,古印度有一个国王,他拥有巨大的财富,但他已经对平淡的生活感到厌倦,渴望着新鲜刺激的事物。
有一天,来了一位老人,他带着自己发明的国际象棋来见国王。国王非常喜欢国际象棋,就对老人说:「你给了我无穷的乐趣,为了奖赏你,我可以满足你的一个愿望。」
老人对国王说:「陛下,请您在棋盘的第 1 个格子赏我 1 粒麦子,在第 2 个格子赏我 2 粒麦子,在第 3 个格子赏我 4 粒麦子……就这样每次增加一倍,一直到第 64 个格子为止。」

国王感觉这太容易了,立即命人去取了 1 袋小麦过来,按照老人的要求给他,结果很快就用完了。接着是第 2 袋、第 3 袋……
后来国王才发现,就算把当时全世界的小麦全部都给他,也无法满足老人的愿望。
有人可能会问:为什么?
这里涉及到一个经典的思维模型:复利思维。
如果你能真正掌握复利思维,并且学以致用,让自己持续获得成长,将来也许就能实现自己的梦想。
2. 什么是复利思维?
复利的计算公式如下:
收益=本金∗(1+收益率)期数收益 = 本金 * ( 1 + 收益率 ) ^ {期数} 收益=本金∗(1+收益率)期数
在国际象棋的故事中,本金相当于 1 粒麦子,收益率是 100%,代入上面的复利公式,第 64 个格子的麦子数量为 263≈9.22337∗10182^{63} ≈ 9.22337 * 10^{18}263≈9.22337∗1018 粒,如果把所有格子的麦子数量加起来,那么麦子总数为 1+2+4+…+263≈1.84467∗10191 + 2 + 4 + … + 2^{63} ≈ 1.84467 * 10^{19}1+2+4+…+263≈1.84467∗1019 粒。
假设 1 粒麦子重约 0.0250.0250.025 克,那么 20000 粒麦子大约为 1斤(500克)1 斤(500 克)1斤(500克)。也就是说,麦子的总重量约为 1.84467∗1019/20000≈9.22335∗10141.84467 * 10^{19} / 20000 ≈ 9.22335 * 10^{14}1.84467∗1019/20000≈9.22335∗1014 斤。
这个数字有多大呢?就算一个人一年吃 500 斤麦子,足够 10 亿人吃上 1800 多年。
股神巴菲特有一个形象的比喻:「人生就像滚雪球,重要的是找到很湿的雪和很长的坡」。
在复利的计算公式中,本金就像是雪球的大小,收益率就像是雪球的湿度,而期数就像是坡道的长度。
复利思维的威力,就像原子弹爆炸一样,能释放出巨大的能量。

3. 如何应用复利思维?
我们看一家企业财务报表的时候,经常会关注资金周转率。如果资金周转得越快,就相当于「雪球」滚得越快。
很多企业采取「小步快跑,快速迭代」的策略,本质上也是在应用复利思维。
在《纳瓦尔宝典》中,有这么一句话:「生活中所有的回报,无论是财富、人际关系、爱情、健康、活动,还是习惯,都来自复利」。
如果把复利思维应用到个人成长上,就是多去做那些能够产生长期积累的事情。
比如,每天深度学习和用心写作,随着时间的拉长,收益将会变得越来越大。
假设你现在的能力水平值是 111,如果你每天进步 1%1\%1%,那么一年以后,你的水平值将是 (1+1%)365≈37.8( 1 + 1\% ) ^ {365} ≈ 37.8(1+1%)365≈37.8,可以说是进步神速。

但反过来,假如你每天退步 11%1,那么一年以后,你的水平值将是 (1−1%)365≈0.03( 1 - 1\% ) ^ {365} ≈ 0.03(1−1%)365≈0.03,所有的才华都将消耗殆尽。
按照复利公式,绘制出来的增长曲线大致如下:
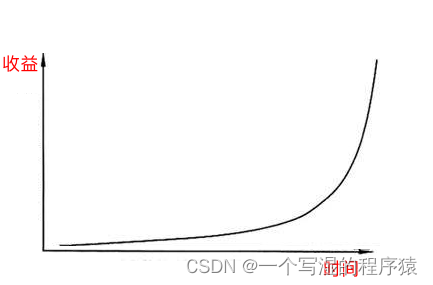
然而,理想很丰满,现实很骨感。
复利的效果在初期并不明显,必须积累足够长的时间之后,才会发生爆发式的增长。在真实世界中的增长,往往呈现为「逻辑函数」S 曲线的样子,因为当增长到达一定高度之后,最终会趋于平稳,而不会一直增长下去。
复利思维高度认可时间的积累价值,所以一定要有耐心,坚持每天学习,刚开始的时候可能没有感觉,几个月之后可能会有眼前一亮的感觉,1 年以后可能会有豁然开朗的感觉, 5 年以后可能会有质的突破。
为了获得更大的收益,我们可以选择自己擅长、感兴趣且有长期价值的事,这样会更有动力持续做下去。
4. 小结
不要把复利当成是一个快速致富的通道,那些把财富自由的希望寄托在复利上的人,基本上都是认知的懒惰者。事实上,复利思维恰恰是长期主义的一种体现。
复利的本质,其实就是我们通常说的「利滚利」,每次都把上一期的利息,作为下一期的本金来计算,就像一个人做事情 A,会导致结果 B,而结果 B 又会反过来加强 A,形成不断增强的回路。
利息的本质,是本金的时间价值。
在真实的世界里,想要实现复利并不容易,不怕收益率低,就怕收益率不稳定,因为收益率的下降,很容易就把增长给吞噬掉。真正考验人的,不是你是否相信复利的存在,而是你能否持续努力做正确的事。
查理·芒格说:「同时理解复利的力量和获得它的困难,是理解许多事情的核心和灵魂」。在有限的时间,把有限的精力和资源,持续投入到某一领域,最终产生的积极影响,会像雪球一样越滚越大,最终可能会大到超乎你的想象。
曾国藩说:「人生唯有常是第一美德」,意思是说:人生的第一美德,是你能坚持做一件正确的事。
这些道理似乎人人都懂,但一旦付诸行动,多数人并没有真正理解时间对于复利的意义。
当你洞察了时间的机制,通过持续深度学习,构建自己的核心竞争力,最终将会收获更加快速的成长。
相关文章:

【思维模型】五分钟了解<复利思维>,为何学习复利思维?什么是复利思维?如何应用复利思维?
【思维模型】五分钟了解<复利思维>,为何学习复利思维?什么是复利思维?如何应用复利思维?1. 为何学习复利思维?2. 什么是复利思维?3. 如何应用复利思维?4. 小结参考&#…...

Vue.js语法详解:从入门到精通
Vue.js是一个流行的JavaScript框架,用于构建用户界面。它的核心特性包括数据双向绑定、组件化架构、虚拟DOM和响应式系统等。在本文中,我们将深入探讨Vue.js的语法,帮助读者更好地理解和应用Vue.js。1.模板语法Vue.js的模板语法采用了类似HTM…...

程序员的代码行数越少越好?
有些人可能会认为,应用程序中的代码行越少,就越容易阅读。这句话只有部分正确,我认为代码可读性的度量标准包括:代码应具备一致性代码应具备自我描述性代码应具备良好的文档代码应使用稳定的现代功能代码不应过于复杂代码的性能不…...

【每日一题Day156】LC1032字符流 | 字典树
字符流【LC1032】 设计一个算法:接收一个字符流,并检查这些字符的后缀是否是字符串数组 words 中的一个字符串。 例如,words ["abc", "xyz"] 且字符流中逐个依次加入 4 个字符 a、x、y 和 z ,你所设计的算法…...
V2G模式下含分布式能源网优化运行研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 📋📋📋本文目录如下:🎁🎁🎁 目录 💥1 概述 📚2 运行结果 &am…...
手写一个简单的RPC框架
学习RPC框架,由繁化简,了解其本质原理 文章目录项目简介什么是RPC?项目模块项目代码common模块client模块server模块framework模块测试项目简介 什么是RPC? RPC(Remote Procedure Call)即远程过程调用&am…...
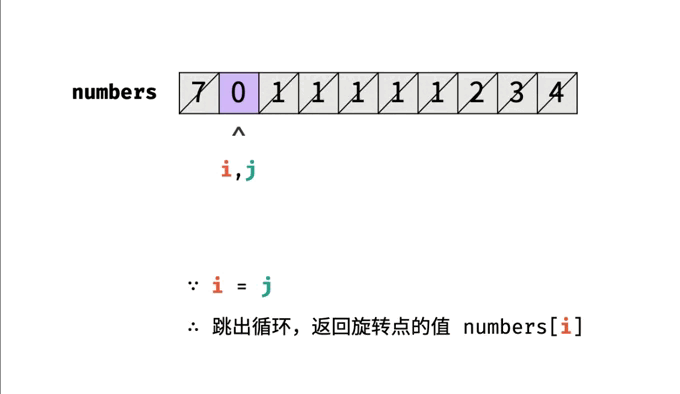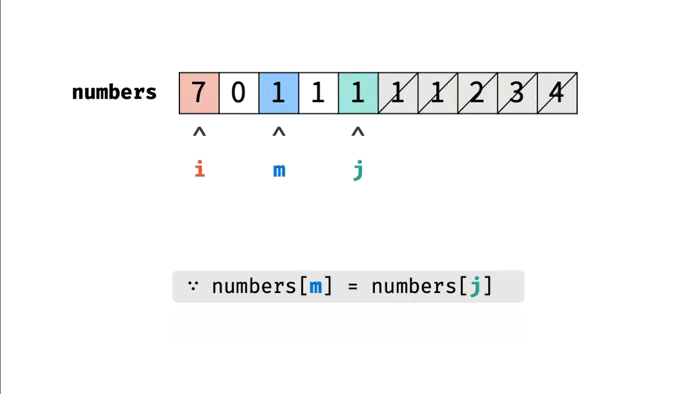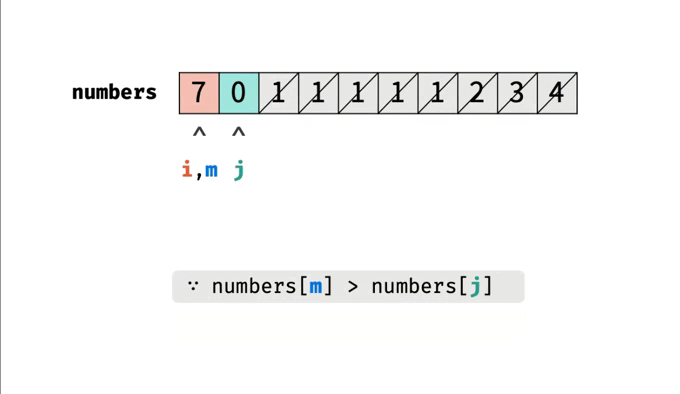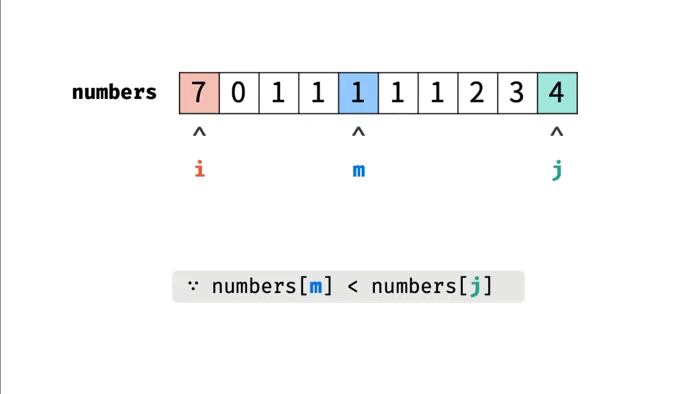
【剑指offer】旋转数组的最小数字
👑专栏内容:剑指offer⛪个人主页:子夜的星的主页💕座右铭:前路未远,步履不停 目录一、题目描述1、题目2、示例示例1示例2二、题目分析1、暴力法2、二分法三、代码汇总1、暴力法2、二分法一、题目描述 1、题…...
【Dorker】Portainer轻量级可视化工具
文章目录Portainer简介登录Portainer第一次登录需创建admin,访问地址:xxx.xxx.xxx.xxx:9000选择local选项卡后本地docker详细信息展示安装nginx私有镜像仓库管理Portainer简介 Portainer是Docker的图形化管理工具,提供状态显示面板、应用模板…...

基于 vue.js 进行组件封装的方案
摘要:本文将介绍如何基于 vue.js 进行组件封装的方案。我们将从分析组件封装的优势开始,然后依次介绍 vue.js 的基本概念,以及如何创建、封装和使用自定义组件。最后,我们将通过一个实际的示例,演示如何实现一个基于 v…...
【Unityc#专题篇】之c#基础篇
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:uni…...
Python(白银时代)——模块、包、异常
异常 概念 程序运行时,如果Python 解释器遇到了错误,会停止程序运行,并且提示错误信息,这就是异常 程序停止执行并提示错误信息的动作,称为 抛出异常 异常捕获 try: 里面的代码,不确定是否能够正常执行. …...

小程序和Vue写法的区别
小程序和Vue写法的区别主要有以下几点: 语法不同:小程序使用的是WXML、WXSS和JS,而Vue使用的是HTML、CSS和JSX。 数据绑定方式不同:小程序使用的是双向数据绑定,而Vue使用的是单向数据流。 1)在小程序中需…...

如何实现分布式锁
一、锁的作用 锁是为了解决多线程情况下,对于共享资源的访问安全问题。 但是当系统是分布式的时候,本地锁已经没法锁住所需要的资源,因为本地获取了锁,其他系统无法得知本地锁的情况。 分布式锁,是独立于系统的第一方…...
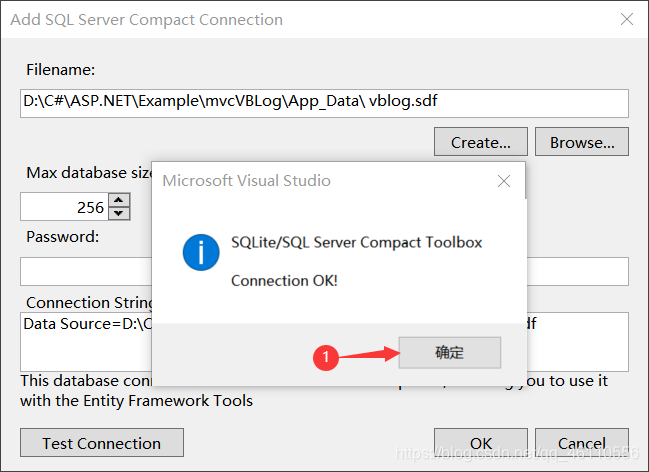
使用VS2019连接Microsoft SQL Server Compact 4.0数据库
简介 SQL Server Compact Edition是微软推出的一个适用于嵌入到移动应用的精简数据库产品,Windows Mobile开发人员能够使用SQL Server CE开发出将数据管理能力延展到Window Mobile移动设备上的应用程序。虽然SQL Server CE占用的磁盘空间只有3到5兆左右,…...

Vue2 和 Vue3 的对比
Vue2 vs Vue3 Vue 是一款流行的 JavaScript 框架,用于构建交互式 Web 界面。Vue2 和 Vue3 是 Vue.js 的两个版本。Vue3 是 Vue.js 的最新版本,于 2020 年 9 月正式发布。Vue3 有许多改进和新功能,下面我们将对 Vue2 和 Vue3 进行比较。 性能…...
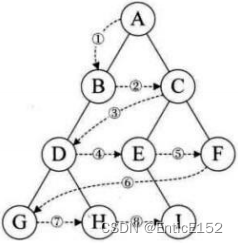
[数据结构]二叉树的链式存储结构
目录 二叉树的链式存储结构:: 1.创建一颗二叉树 2.二叉搜索树简介 3.前序、中序以及后序遍历 4.层序遍历 5.求一棵树的节点个数代码实现 6.求一棵树的高度代码实现 7.求叶子节点个数代码实现 8.求第K层节点个数代码实现 9.二叉树查找值为x的节点 二叉树…...

黑马程序员 Redis 踩坑及解决
文章目录实战篇p30 短信登录-隐藏用户敏感信息p50 优惠券秒杀-添加优惠券p69 秒杀优化-异步秒杀思路p81 达人探店-点赞排行榜p87 好友关注-实现滚动分页查询问题 1问题 2p90 附近商铺-实现附近商户功能实战篇 p30 短信登录-隐藏用户敏感信息 问题描述:登录后会跳转…...

Matlab实现粒子群算法
粒子群算法(Particle Swarm Optimization,PSO)是一种群体智能算法,通过模拟自然界中鸟群、鱼群等生物群体的行为,来解决优化问题。 在PSO算法中,每个个体被称为粒子,每个粒子的位置表示解空间中…...

tailwindcss 写原生html
需要注意:html文件中引入的是output.css input.css写那三行预留的就可以了打包的时候只要打包html output.css img文件夹句ok,其他都不用原理是运行时生产output.css文件,直接【注意!注意!注意!class"…...

Java开发一年不到,来面试居然敢开口要20K,面完连8K都不想给~
前言 我的好朋友兼大学同学老伍家庭经济情况不错,毕业之后没两年自己存了点钱加上家里的支持,自己在杭州开了一家网络公司。由于公司不是很大所以公司大部分的开发人员都是自己面试的,近期公司发展的不错,打算扩招也面试了不少人…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...
