[数据结构]二叉树的链式存储结构
目录
二叉树的链式存储结构::
1.创建一颗二叉树
2.二叉搜索树简介
3.前序、中序以及后序遍历
4.层序遍历
5.求一棵树的节点个数代码实现
6.求一棵树的高度代码实现
7.求叶子节点个数代码实现
8.求第K层节点个数代码实现
9.二叉树查找值为x的节点
二叉树的链式存储结构::
1.创建一颗二叉树
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
BTNode* CreateTree()
{BTNode* n1 = (BTNode*)malloc(sizeof(BTNode));assert(n1);BTNode* n2 = (BTNode*)malloc(sizeof(BTNode));assert(n2);BTNode* n3 = (BTNode*)malloc(sizeof(BTNode));assert(n3);BTNode* n4 = (BTNode*)malloc(sizeof(BTNode));assert(n4);BTNode* n5 = (BTNode*)malloc(sizeof(BTNode));assert(n5);BTNode* n6 = (BTNode*)malloc(sizeof(BTNode));assert(n6);n1->data = 1;n2->data = 2;n3->data = 3;n4->data = 4;n5->data = 5;n6->data = 6;n1->left = n2;n1->right = n4;n2->left = n3;n2->right = NULL;n4->left = n5;n4->right = n6;n3->left = NULL;n3->right = NULL;n5->left = NULL;n5->right = NULL;n6->left = NULL;n6->right = NULL;return n1;
}注意:上述代码并不是创建二叉树的方式,真正创建二叉树方式后续重点讲解。
2.二叉搜索树简介
二叉搜索树:
若它的左子树不为空,则左子树上的所有节点的值均小于它的根节点的值,若它的右子树不空,
则右子树上所有节点的值均大于它的根节点的值,它的左右子树也分别为二叉排序树,二叉搜索树
作为一种经典的数据结构,它既有链表的快速插入与删除操作的特点又有数组快速查找的优势,所以应用十分广泛,例如在文件系统和数据库系统一般会采用这种数据结构进行高效率的排序与检索操作,因此,二叉搜索树的增删查改才有意义,普通二叉树的增删查改价值不大。

3.前序、中序以及后序遍历
学习二叉树结构,最简单的方式就是遍历,所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树的节点进行相应的操作,并且每个节点只操作一次。访问节点所做的操作依赖于具体的应用问题。遍历是二叉树最重要的运算之一,也是二叉树上进行其他运算的基础。
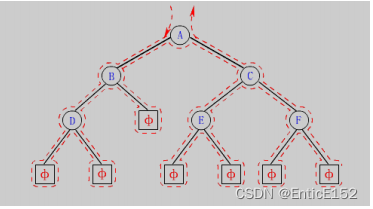
按照规则,二叉树的遍历有:前序、中序、后序的递归结构遍历:
1.前序遍历(PreOrder Traversal 亦称先序遍历):访问根节点的操作发生在遍历其左右子树之前
2.中序遍历(InOrder Traversal):访问根节点的操作发生在遍历其左右子树之间
3.后序遍历(PostOrder Traversal):访问根节点的操作发生在遍历其左右子树之后
由于被访问的节点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树、根的右子树。NLR、LNR、LRN分别又称为先根遍历、中根遍历和后根遍历。
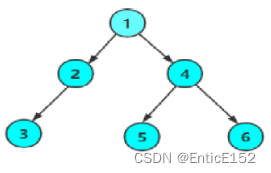
前序遍历结果:1 2 3 4 5 6

中序遍历结果:3 2 1 5 4 6

后序遍历结果:3 2 5 6 4 1
![]()
前序遍历递归图解:
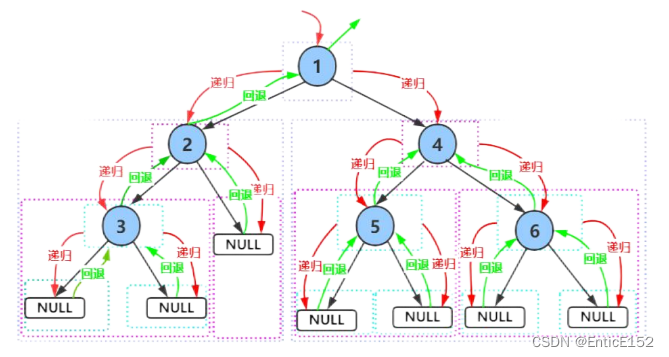
//二叉树的前序遍历
void PreOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%d ", root->data);PreOrder(root->left);PreOrder(root->right);
}
//二叉树的中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}
//二叉树的后序遍历
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}4.层序遍历
//层序遍历
//利用队列的性质,将父亲节点入队列,出队列的时候,将其孩子入队列(上一层节点出的时候代入下一层)
//注:队列需要二叉树的节点定义,二叉树层序遍历需要队列,在此需要解决相互包含的问题,所以要将二叉树的节点定义放到Queue.h中
//复制粘贴队列代码
Queue.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
typedef BTNode* QDataType;
typedef struct QueueNode
{struct QueueNode* next;QDataType data;
}QNode;
//第三种不用二级指针的方式 封装成结构体
typedef struct Queue
{QNode* head;QNode* tail;int size;
}Queue;
void QueueInit(Queue* pq);
void QueueDestory(Queue* pq);
void QueuePush(Queue* pq, QDataType x);
void QueuePop(Queue* pq);
//取队列头部数据
QDataType QueueFront(Queue* pq);
//取队列尾部数据
QDataType QueueBack(Queue* pq);
bool QueueEmpty(Queue* pq);
int QueueSize(Queue* pq);
void TreelevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){//取队头数据 这里队列中的数据是指针BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->data);//下一层入队列if (front->left)QueuePush(&q, front->left);if (front->right)QueuePush(&q, front->right);}printf("\n");QueueDestory(&q);
}
Queue.c
#include"Queue.h"
void QueueInit(Queue* pq)
{assert(pq);pq->head = pq->tail = NULL;pq->size = 0;
}
void QueueDestory(Queue* pq)
{assert(pq);QNode* cur = pq->head;while (cur){QNode* del = cur;cur = cur->next;free(del);}pq->head = pq->tail = NULL;
}
void QueuePush(Queue* pq, QDataType x)
{assert(pq);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc fail");exit(-1);}else{newnode->data = x;newnode->next = NULL;}if (pq->tail == NULL){pq->head = pq->tail = newnode;}else{pq->tail->next = newnode;pq->tail = newnode;}pq->size++;
}
void QueuePop(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));if (pq->head->next == NULL){free(pq->head);pq->head = pq->tail = NULL;}else{QNode* del = pq->head;pq->head = pq->head->next;free(del);del = NULL;}pq->size--;
}
//取队列头部数据
QDataType QueueFront(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->head->data;
}
//取队列尾部数据
QDataType QueueBack(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->tail->data;
}
bool QueueEmpty(Queue* pq)
{assert(pq);return pq->head == NULL && pq->tail == NULL;
}
int QueueSize(Queue* pq)
{assert(pq);/*QNode* cur = pq->head;int n = 0;while (cur){++n;cur = cur->next;}return n;*/return pq->size;
}
void TreelevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){//取队头数据 这里队列中的数据是指针BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->data);//下一层入队列if (front->left)QueuePush(&q, front->left);if (front->right)QueuePush(&q, front->right);}printf("\n");QueueDestory(&q);
}选择题练习:
1.某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。该完全二叉树的前序序列为()
A ABDHECFG
B ABCDEFGH
C HDBEAFCG
D HDEBFGCA
2.二叉树的先序遍历和中序遍历如下:先序遍历:EFHIGJK;中序遍历:HFIEJKG.则二叉树根结点为()
A E
B F
C G
D H
3.设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树前序遍历序列为____。
A adbce
B decab
C debac
D abcde
4.某二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,则按层次输出(同一层从左到右)的序列为
A FEDCBA
B CBAFED
C DEFCBA
D ABCDEF
答案:
A
A
D
A5.求一棵树的节点个数代码实现
//求一棵树的节点个数
//遍历计数的缺陷:
//静态成员变量只会在定义时初始化一次
int TreeSize(BTNode* root)
{static int count = 0;if (root == NULL)return count;++count;TreeSize(root->left);TreeSize(root->right);return count;
}
//遍历计数的缺陷:
//全局变量
//调用时依旧要注意 count初始化一下 因为生命周期在全局 作用域在这个函数
int count = 0;
void TreeSize(BTNode* root)
{if (root == NULL)return;++count;TreeSize(root->left);TreeSize(root->right);return;
}
int main()
{printf("Tree Size:%d\n", TreeSize(root));printf("Tree Size:%d\n", TreeSize(root));count = 0;TreeSize(root);printf("Tree Size:%d\n", root);count = 0;TreeSize(root);printf("Tree Size:%d\n", root);return 0;
}
//子问题思路解决
int TreeSize(BTNode* root)
{//注意:一定是TreeSize(root->left)和TreeSize(root->right)都返回值时,才+1在往上一层返回return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
6.求一棵树的高度代码实现
//求树的高度
//父亲的高度 = 左右子树的高度大的 + 1
int TreeHeight(BTNode* root)
{if (root == NULL){return 0;}int leftHeight = TreeHeight(root->left);int rightHeight = TreeHeight(root->right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}7.求叶子节点个数代码实现
//求叶子节点的个数
int TreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return TreeLeafSize(root->left) + TreeLeafSize(root->right);}8.求第K层节点个数代码实现
//求第K层节点个数
//转换成求左右子树的第K-1层
int TreeKLevel(BTNode* root, int k)
{assert(k > 0);if (root == NULL){return 0;}if (k == 1){return 1;}//转换成求子树的第k-1层return Tree(root->left, k - 1) + TreeLevel(root->right, k - 1);
}
9.二叉树查找值为x的节点
//返回x所在的节点
//该代码是一个前序查找的过程
BTNode* TreeFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}//一定要用返回值接收递归的结果 不然就要递归调用一次自己BTNode* leftRet = TreeFind(root->left, x);//先去左树找 找到了就返回if (leftRet != NULL){return leftRet;}//左树没有找到再到右树找BTNode* rightRet = TreeFind(root->right, x);if (rightRet != NULL){return rightRet;}return NULL;
}
代码简化:
BTNode* TreeFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}//一定要用返回值接收递归的结果 不然就要递归调用一次自己BTNode* leftRet = TreeFind(root->left, x);//先去左树找 找到了就返回if (leftRet != NULL){return leftRet;}//递归右树 找到了就返回 找不到就返回NULLreturn TreeFind(root->right, x);
}相关文章:

[数据结构]二叉树的链式存储结构
目录 二叉树的链式存储结构:: 1.创建一颗二叉树 2.二叉搜索树简介 3.前序、中序以及后序遍历 4.层序遍历 5.求一棵树的节点个数代码实现 6.求一棵树的高度代码实现 7.求叶子节点个数代码实现 8.求第K层节点个数代码实现 9.二叉树查找值为x的节点 二叉树…...

黑马程序员 Redis 踩坑及解决
文章目录实战篇p30 短信登录-隐藏用户敏感信息p50 优惠券秒杀-添加优惠券p69 秒杀优化-异步秒杀思路p81 达人探店-点赞排行榜p87 好友关注-实现滚动分页查询问题 1问题 2p90 附近商铺-实现附近商户功能实战篇 p30 短信登录-隐藏用户敏感信息 问题描述:登录后会跳转…...

Matlab实现粒子群算法
粒子群算法(Particle Swarm Optimization,PSO)是一种群体智能算法,通过模拟自然界中鸟群、鱼群等生物群体的行为,来解决优化问题。 在PSO算法中,每个个体被称为粒子,每个粒子的位置表示解空间中…...

tailwindcss 写原生html
需要注意:html文件中引入的是output.css input.css写那三行预留的就可以了打包的时候只要打包html output.css img文件夹句ok,其他都不用原理是运行时生产output.css文件,直接【注意!注意!注意!class"…...

Java开发一年不到,来面试居然敢开口要20K,面完连8K都不想给~
前言 我的好朋友兼大学同学老伍家庭经济情况不错,毕业之后没两年自己存了点钱加上家里的支持,自己在杭州开了一家网络公司。由于公司不是很大所以公司大部分的开发人员都是自己面试的,近期公司发展的不错,打算扩招也面试了不少人…...
LeetCode题解 20(17,79) 电话号码的字母组合,单词搜索<回溯>
文章目录电话号码的字母组合(17)代码解答单词搜索(79)代码解答电话号码的字母组合(17) 思路: 根据题意我们必须根据数字获取对应的字符数组,因此我们先定义1个字符数组表示这个电话表 private String[] letters {"","","abc","…...
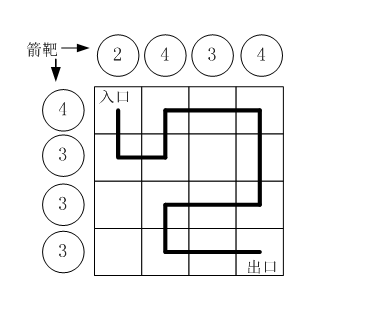
路径之谜 蓝桥杯 89
题目描述小明冒充 X 星球的骑士,进入了一个奇怪的城堡。城堡里边什么都没有,只有方形石头铺成的地面。假设城堡地面是 nn 个方格。如下图所示。按习俗,骑士要从西北角走到东南角。可以横向或纵向移动,但不能斜着走,也不…...

Mysql数据库如何调优
MYSQL数据库调优 索引 1、对于常用的查询字段加索引,但如果常用字段只有几个常量值就不需要加索引,或者使用索引会失效的情况; 2、索引失效的情况: 1、索引列使用函数,计算(加减乘除等) …...
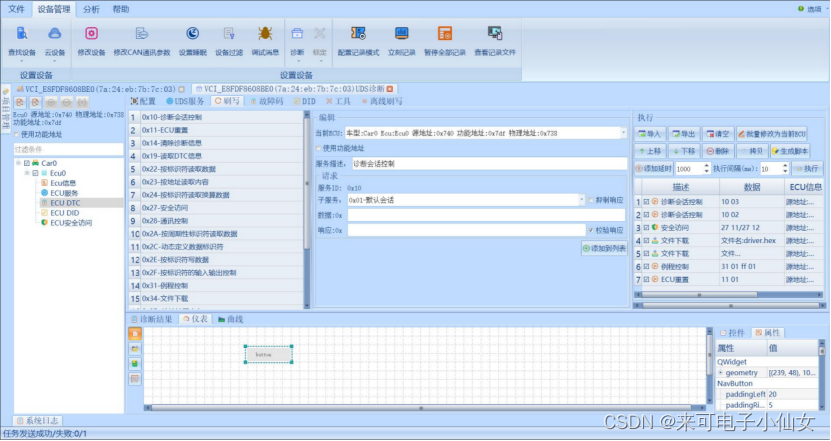
CAN(FD)记录仪在新能源汽车整车控制器(VCU)、电池管理系统(BMS)、电机控制器(MCU)、发动机ECU中的应用,免去出差烦恼
今天介绍CAN(FD)记录仪在新能源汽车整车控制器(VCU)、电池管理系统(BMS)、电机控制器(MCU)、发动机ECU中的应用 第一步:新能源汽车整车控制器(VCU)先供上电,…...

【设计模式】23种设计模式之七大原则
【设计模式】23种设计模式之七大原则什么是设计模式的原则1、单一职责原则基本介绍案例分析注意事项2、接口隔离原则基本介绍案例分析代码实现3、依赖倒转原则基本介绍案例分析依赖传递的三种方式注意事项4、里氏替换原则关于继承性的思考和说明基本介绍案例分析5、开闭原则ocp…...

python - 文件操作
1. 概念 计算机内存通常分为两种类型:主存储器和辅助存储器。 主存储器是计算机中最重要的存储器类型之一。它是计算机中用于存储正在运行的程序和数据的存储器。主存储器通常是易失性的,这意味着当计算机关闭时,其中存储的数据将被删除。主存…...

docker打包golang应用
一、错误的打包方式在本地环境编译,然后将可执行程序放入 alpine(docker.io/alpine:latest)准备web程序package mainimport ("fmt""net/http" )func main() {server : &http.Server{Addr: ":8888",}http.HandleFunc("/"…...

redis 内容总结
目录redis 内容列举Redis和Memcached比较Redis简介1、Redis 数据结构2、Redis的持久化机制3、Redis 内容管理(淘汰策略/删除策略)4、Redis 事务5、Redis 缓存三大问题6、Redis 集群7、Redis 应用redis 内容列举 官网:https://redis.io/ 中文…...
贪心算法(一)
一、概念 贪心算法的核心思想是,在处理一个大问题时,划分为多个局部并在每个局部选择最优解,并且认为在每个局部选择最优解,那么最后全局的问题得到的就是最优解。 贪心算法可以解决一些问题,但是不适用于所有问题&a…...

【栈和队列OJ题】有效的括号用队列实现栈用栈实现队列设计循环队列
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:数据结构 🎯长路漫漫浩浩,万事皆有期待 文章目录OJ题1.有效的括号1.1…...
kuernetes 资源对象分析报错
文章目录1. pod 状态1.1 容器启动错误类型1.2 ImagePullBackOff 错误1.3 CrashLoopBackOff1.4 Pending2. Service 连接状态3. Ingress 连接状态1. pod 状态 创建一个 pod-status.yaml apiVersion: v1 kind: Pod metadata:name: runninglabels:app: nginx spec:containers:- na…...

动态内存的开辟
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练,题解C,C的使用文章,「初学」C 🔥座右铭:“不要等到什么都没有了,才下…...

【蓝桥杯-筑基篇】搜索
🍓系列专栏:蓝桥杯 🍉个人主页:个人主页 目录 递归树 1.递归构建二进制串 2.全排列的 DFS 解法 3.全排列的 BFS 解法 4.数的划分法 5.图书推荐 递归树 递归树是一种用于分析递归算法时间复杂度的工具。它可以将递归算法的执行过程可视化…...

week5-质数-最大公约数-快速幂-组合计数-博弈论
蓝桥 等差数列——欧几里得算法质数质数的判定——试除法分解质因数——试除法筛质数——埃氏筛法筛质数——线性筛法质数问题质数距离约数试除法求约数约数个数约数之和最大公约数-欧几里得算法(辗转相除法)扩展欧几里得算法裴蜀定理应用——线性同余方程消灭老鼠Hankson的趣…...
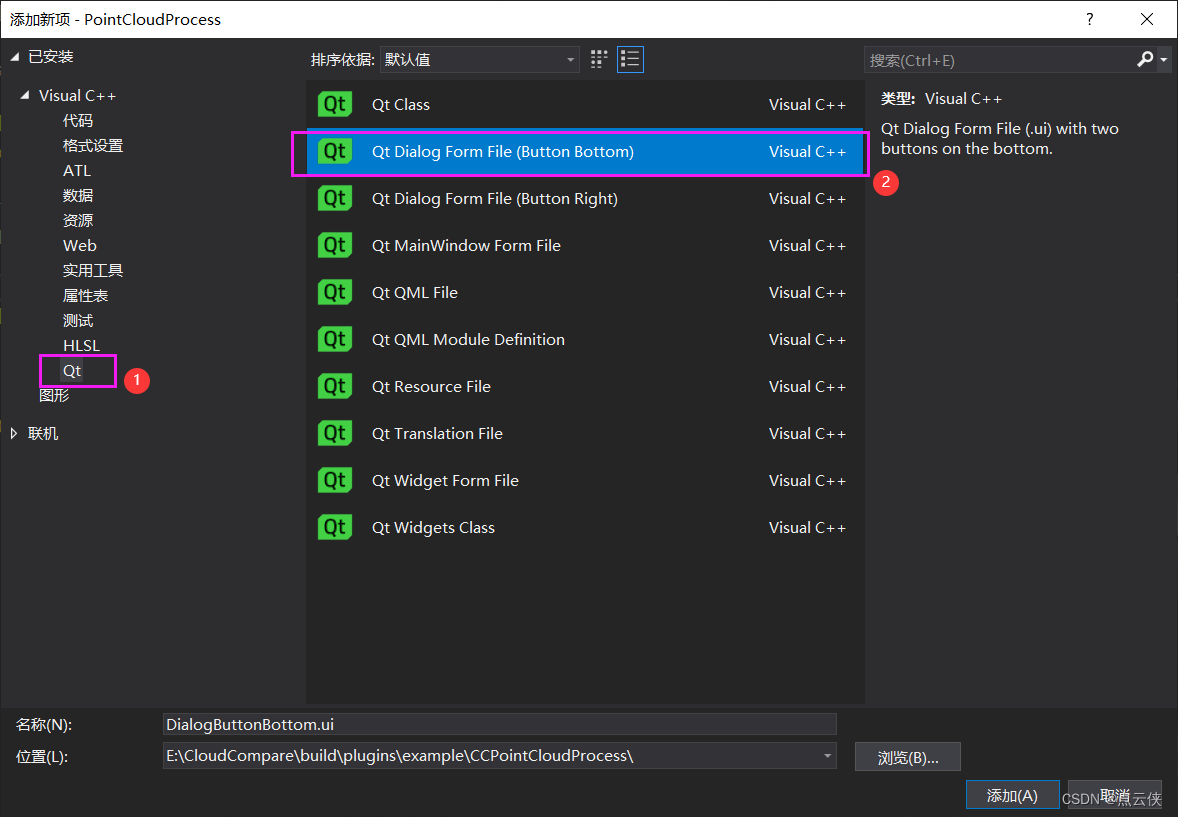
CloudCompare 二次开发(6)——插件中拖拽添加Qt窗口(区域生长算法为例)
目录 一、概述二、插件制作三、Cmake编译四、插件代码五、结果展示一、概述 手动拖拽的方式搭建Qt对话框界面的制作流程,以PCL中的点云区域生长算法为例进行制作。 二、插件制作 1、将....\plugins\example路径下的ExamplePlugin复制一份并修改名字为CCPointCloudProcess。 …...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

