路径之谜 蓝桥杯 89
题目描述
小明冒充 X 星球的骑士,进入了一个奇怪的城堡。
城堡里边什么都没有,只有方形石头铺成的地面。
假设城堡地面是 n×n 个方格。如下图所示。
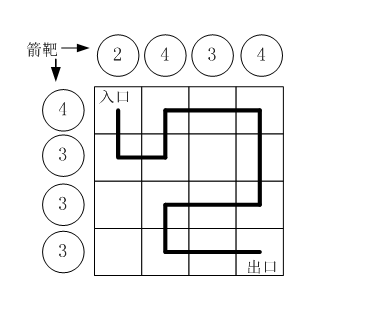
按习俗,骑士要从西北角走到东南角。可以横向或纵向移动,但不能斜着走,也不能跳跃。每走到一个新方格,就要向正北方和正西方各射一箭。(城堡的西墙和北墙内各有 n 个靶子)同一个方格只允许经过一次。但不必走完所有的方格。如果只给出靶子上箭的数目,你能推断出骑士的行走路线吗?有时是可以的,比如上图中的例子。
本题的要求就是已知箭靶数字,求骑士的行走路径(测试数据保证路径唯一)
输入描述
第一行一个整数 N (0≤≤200≤N≤20),表示地面有 N×N 个方格。
第二行 N 个整数,空格分开,表示北边的箭靶上的数字(自西向东)
第三行 N 个整数,空格分开,表示西边的箭靶上的数字(自北向南)
输出描述
输出一行若干个整数,表示骑士路径。
为了方便表示,我们约定每个小格子用一个数字代表,从西北角开始编号: 0,1,2,3 ⋯⋯
比如,上图中的方块编号为:
0 1 2 3
4 5 6 7
8 9 10 11
12 13 14 15
输入输出样例
示例
输入
4
2 4 3 4
4 3 3 3输出
0 4 5 1 2 3 7 11 10 9 13 14 15dfs搜索,区别是多了一个栈来记录路径
def dfs(x,y):if a[x]<0 or b[y]<0:#步数已经用完return if x==n-1 and y==n-1:#到最后一格jieshu =1for i in range(n):if a[i]!=0 or b[i]!=0:#不满足条件跳出jieshu = 0returnif jieshu==1:#满足条件,输出路径for i in range(len(path)):print(path[i],end=' ')for d in [(1,0),(-1,0),(0,1),(0,-1)]:tx ,ty= x+d[0],y+d[1]if 0<= tx <n and 0<=ty<n and vis[tx][ty]==0:vis[tx][ty]=1path.append(tx*n+ty)#每一个格子的算法 因为起点是[0][0],所以每个格子的数字是tx*n+tya[tx]-=1b[ty]-=1dfs(tx,ty)path.pop()#恢复a[tx]+=1b[ty]+=1vis[tx][ty]=0
n=int(input())
vis = [[0]*n for i in range(n)]
path = []
path.append(0)
b = list(map(int,input().split()))
a = list(map(int,input().split()))
vis[0][0]=1#标记第一个格子
a[0]-=1#给第一行和第一列的计数减一
b[0]-=1
dfs(0,0)相关文章:

路径之谜 蓝桥杯 89
题目描述小明冒充 X 星球的骑士,进入了一个奇怪的城堡。城堡里边什么都没有,只有方形石头铺成的地面。假设城堡地面是 nn 个方格。如下图所示。按习俗,骑士要从西北角走到东南角。可以横向或纵向移动,但不能斜着走,也不…...

Mysql数据库如何调优
MYSQL数据库调优 索引 1、对于常用的查询字段加索引,但如果常用字段只有几个常量值就不需要加索引,或者使用索引会失效的情况; 2、索引失效的情况: 1、索引列使用函数,计算(加减乘除等) …...
CAN(FD)记录仪在新能源汽车整车控制器(VCU)、电池管理系统(BMS)、电机控制器(MCU)、发动机ECU中的应用,免去出差烦恼
今天介绍CAN(FD)记录仪在新能源汽车整车控制器(VCU)、电池管理系统(BMS)、电机控制器(MCU)、发动机ECU中的应用 第一步:新能源汽车整车控制器(VCU)先供上电,…...

【设计模式】23种设计模式之七大原则
【设计模式】23种设计模式之七大原则什么是设计模式的原则1、单一职责原则基本介绍案例分析注意事项2、接口隔离原则基本介绍案例分析代码实现3、依赖倒转原则基本介绍案例分析依赖传递的三种方式注意事项4、里氏替换原则关于继承性的思考和说明基本介绍案例分析5、开闭原则ocp…...

python - 文件操作
1. 概念 计算机内存通常分为两种类型:主存储器和辅助存储器。 主存储器是计算机中最重要的存储器类型之一。它是计算机中用于存储正在运行的程序和数据的存储器。主存储器通常是易失性的,这意味着当计算机关闭时,其中存储的数据将被删除。主存…...

docker打包golang应用
一、错误的打包方式在本地环境编译,然后将可执行程序放入 alpine(docker.io/alpine:latest)准备web程序package mainimport ("fmt""net/http" )func main() {server : &http.Server{Addr: ":8888",}http.HandleFunc("/"…...

redis 内容总结
目录redis 内容列举Redis和Memcached比较Redis简介1、Redis 数据结构2、Redis的持久化机制3、Redis 内容管理(淘汰策略/删除策略)4、Redis 事务5、Redis 缓存三大问题6、Redis 集群7、Redis 应用redis 内容列举 官网:https://redis.io/ 中文…...
贪心算法(一)
一、概念 贪心算法的核心思想是,在处理一个大问题时,划分为多个局部并在每个局部选择最优解,并且认为在每个局部选择最优解,那么最后全局的问题得到的就是最优解。 贪心算法可以解决一些问题,但是不适用于所有问题&a…...

【栈和队列OJ题】有效的括号用队列实现栈用栈实现队列设计循环队列
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:数据结构 🎯长路漫漫浩浩,万事皆有期待 文章目录OJ题1.有效的括号1.1…...
kuernetes 资源对象分析报错
文章目录1. pod 状态1.1 容器启动错误类型1.2 ImagePullBackOff 错误1.3 CrashLoopBackOff1.4 Pending2. Service 连接状态3. Ingress 连接状态1. pod 状态 创建一个 pod-status.yaml apiVersion: v1 kind: Pod metadata:name: runninglabels:app: nginx spec:containers:- na…...

动态内存的开辟
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练,题解C,C的使用文章,「初学」C 🔥座右铭:“不要等到什么都没有了,才下…...

【蓝桥杯-筑基篇】搜索
🍓系列专栏:蓝桥杯 🍉个人主页:个人主页 目录 递归树 1.递归构建二进制串 2.全排列的 DFS 解法 3.全排列的 BFS 解法 4.数的划分法 5.图书推荐 递归树 递归树是一种用于分析递归算法时间复杂度的工具。它可以将递归算法的执行过程可视化…...

week5-质数-最大公约数-快速幂-组合计数-博弈论
蓝桥 等差数列——欧几里得算法质数质数的判定——试除法分解质因数——试除法筛质数——埃氏筛法筛质数——线性筛法质数问题质数距离约数试除法求约数约数个数约数之和最大公约数-欧几里得算法(辗转相除法)扩展欧几里得算法裴蜀定理应用——线性同余方程消灭老鼠Hankson的趣…...
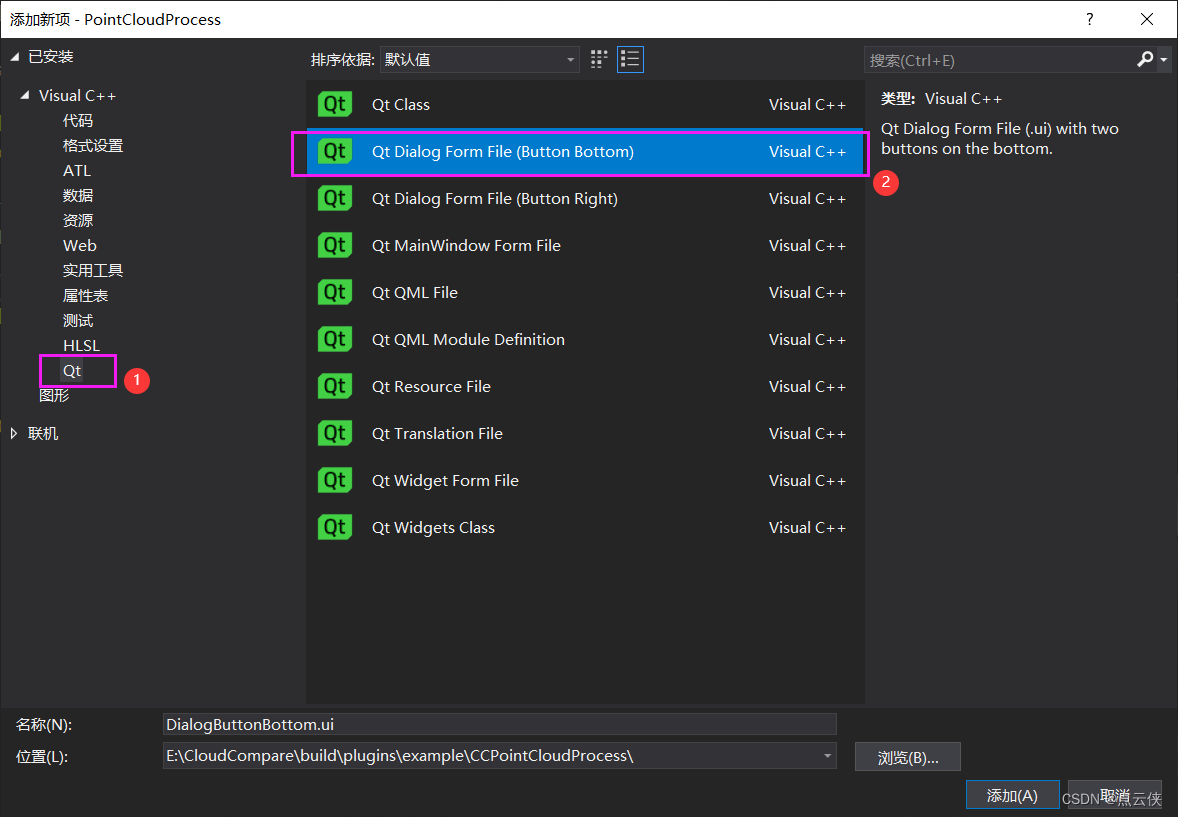
CloudCompare 二次开发(6)——插件中拖拽添加Qt窗口(区域生长算法为例)
目录 一、概述二、插件制作三、Cmake编译四、插件代码五、结果展示一、概述 手动拖拽的方式搭建Qt对话框界面的制作流程,以PCL中的点云区域生长算法为例进行制作。 二、插件制作 1、将....\plugins\example路径下的ExamplePlugin复制一份并修改名字为CCPointCloudProcess。 …...

2023值得推荐的高颜值Vue3.0 Web PC端UI框架,赶紧收藏学习!
Hello,我是前端胡说,本期给大家带来2023值得推荐的Vue3.0 UI组件库,希望大家喜欢! Vue3 正式发布已经有一段时间了,2022年2月也正式变成 Vue 项目的默认版本。在过去一年多的时间里,各大组件库、框架也紧跟…...
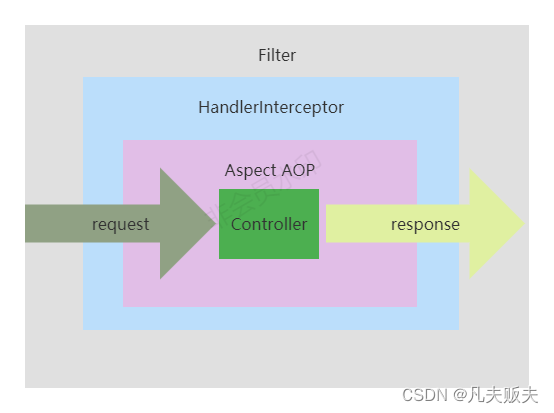
Springboot项目Aop、拦截器、过滤器横向对比
前言伟人曾经说过,没有调查就没有发言权(好像是伟人说的,不管谁说的,这句话是正确的),有些东西看着简单,张口就来,但很有可能是错的。我个人的经验是,aop、过滤器、拦截器的实现方式很简单&…...
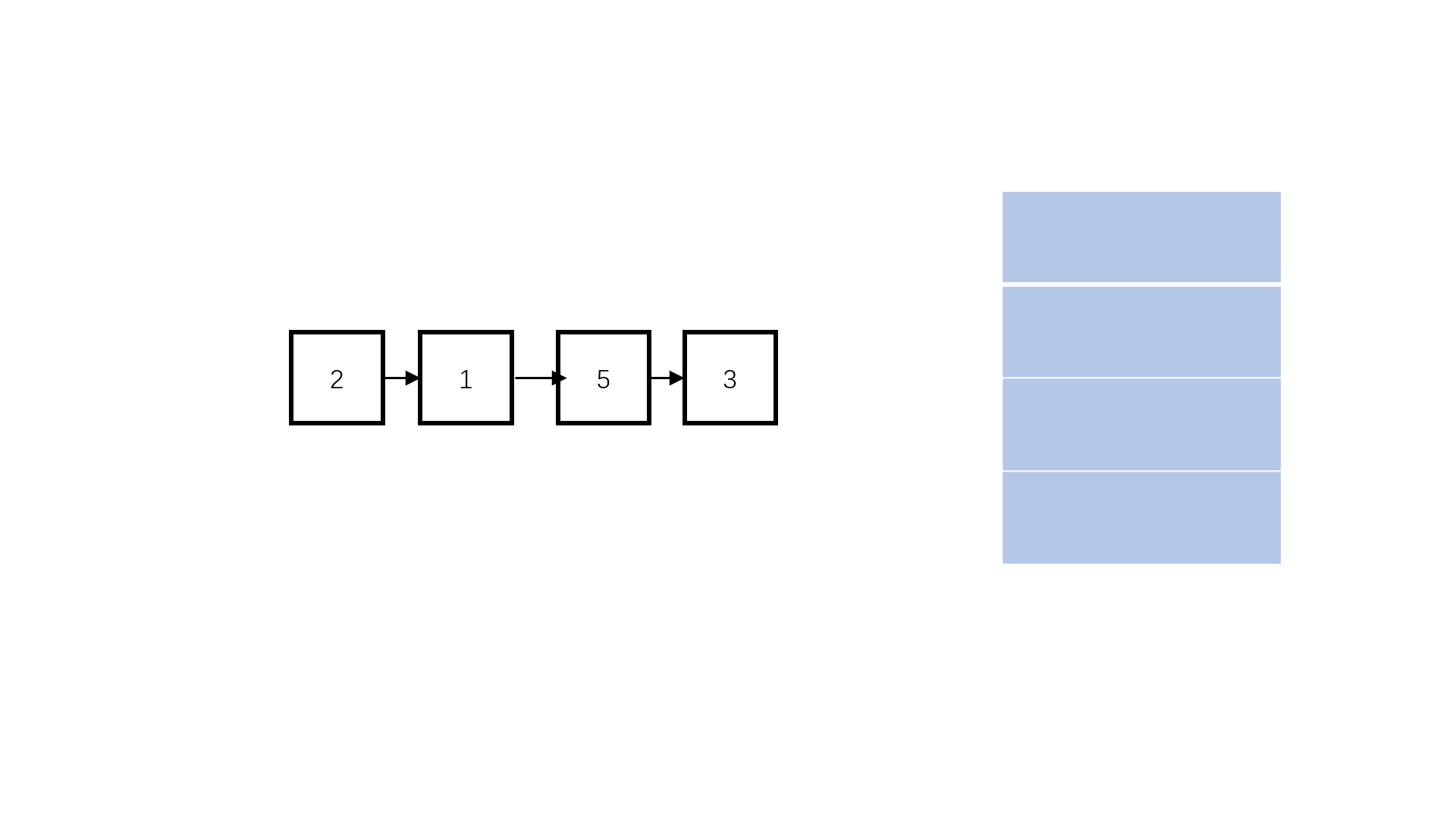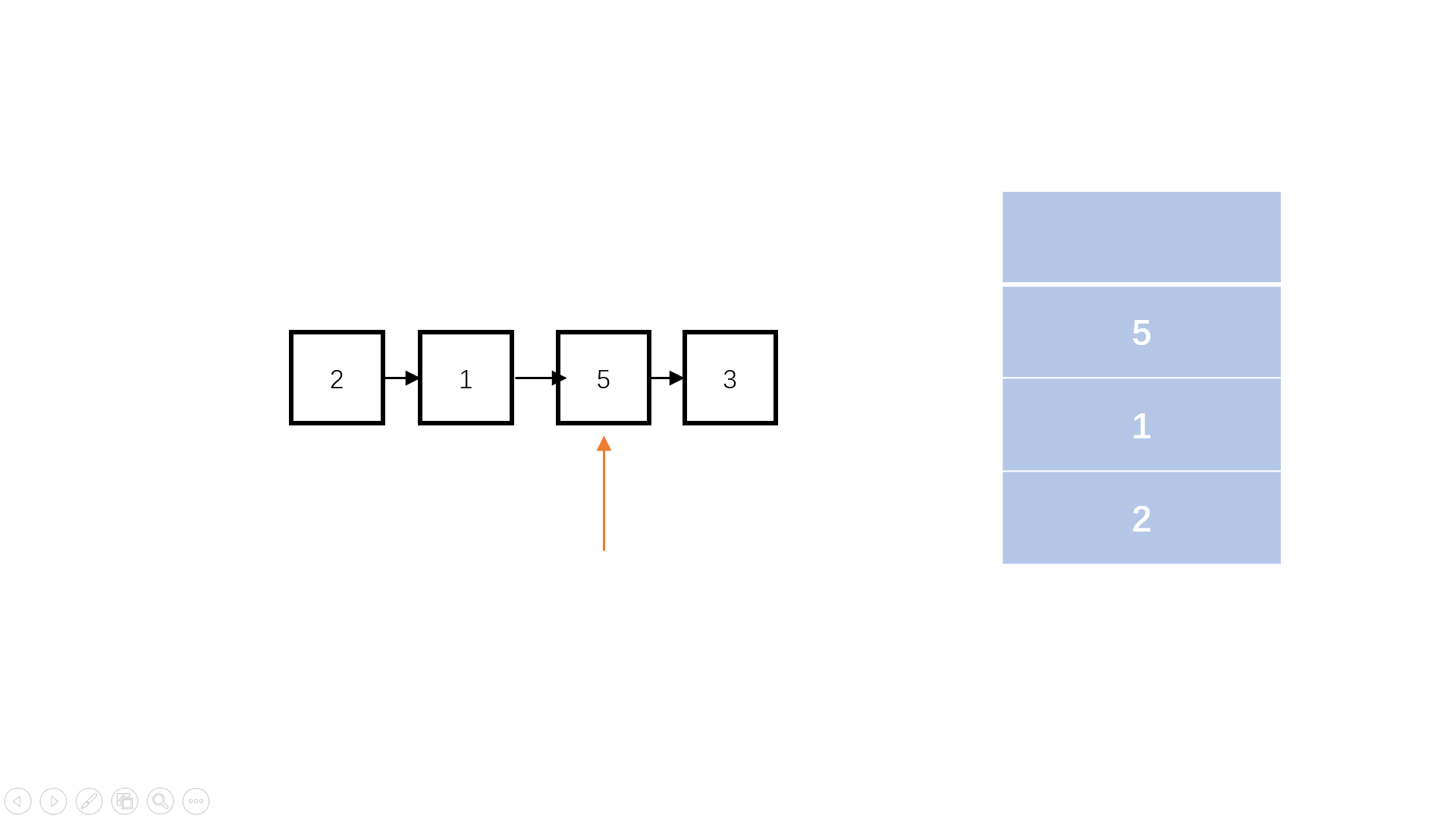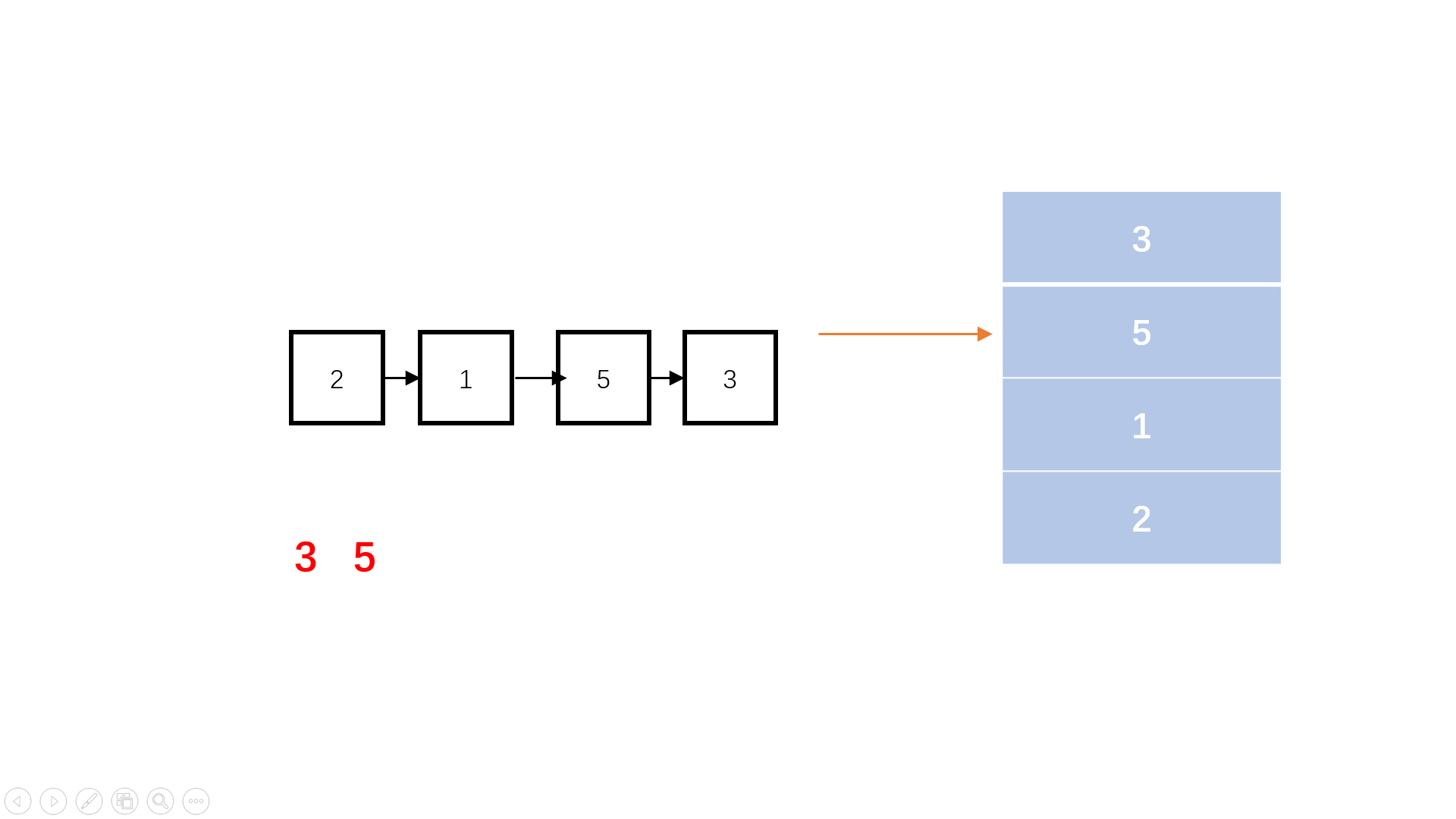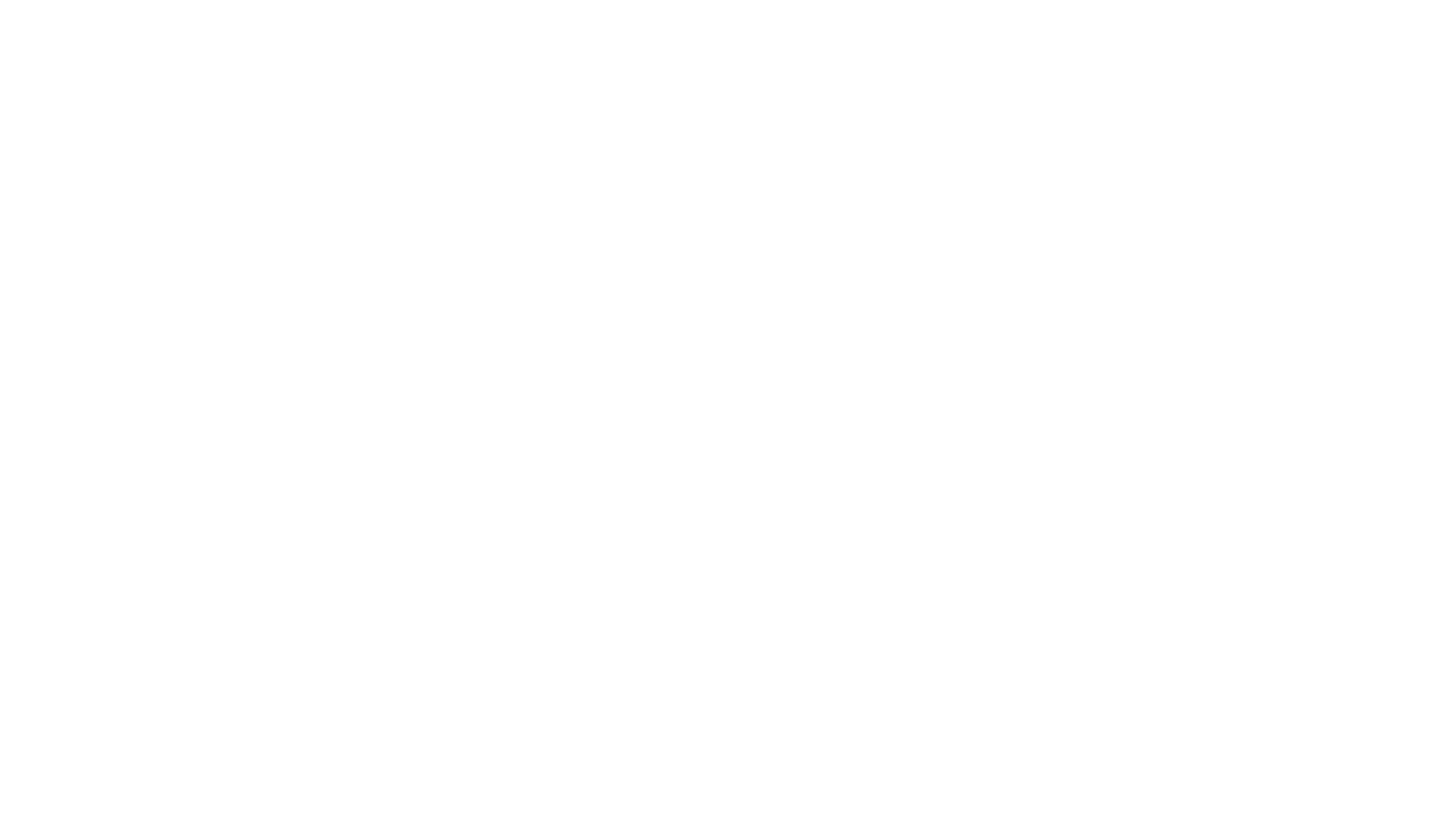
为了之后找工作不被虐,每天刷3道《剑指offer》Day-1
本文已收录于专栏🌻《刷题笔记》文章目录前言💖 1、二维数组中的查找题目描述思路💖 2、替换空格题目描述思路💖 3、从尾到头打印链表题目描述思路一(反转函数)思路二(递归)思路二&a…...

Linux-磁盘管理介绍
Linux-磁盘管理介绍 计算硬盘介绍 硬盘是计算机主要存储媒介之一,由一个或者多个铝制或者玻璃制的碟片组成,碟片外覆盖有铁磁性材料,硬盘内部由磁道、柱面、扇区、磁头等部件组成; cylinder:柱面sector:扇区 磁道与…...
爬虫架构(一):爬虫中的去重处理
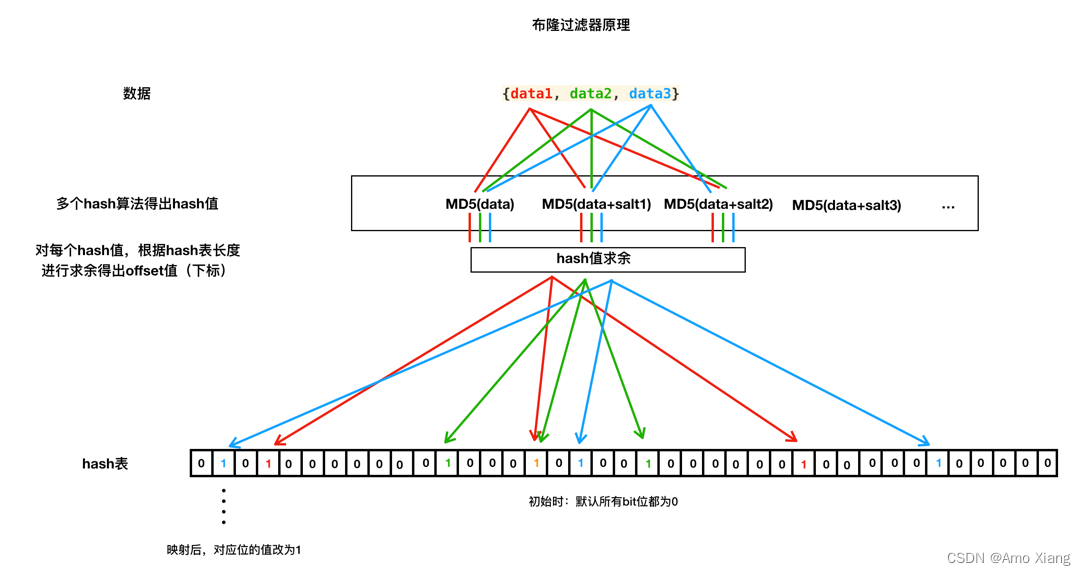
目录一、概要二、去重应用场景以及基本原理2.1 爬虫中什么业务需要使用去重2.2 去重实现的基本原理2.3 根据原始数据进行去重判断2.4 根据原始数据的特征值进行去重判断2.5 临时去重容器与持久化去重容器2.6 常用几种特殊的原始数据特征值计算三、基于信息摘要算法的去重3.1 信…...

算法刷题总结 (二) 回溯与深广搜算法
算法总结2 回溯与深广搜算法一、理解回溯算法1.1、回溯的概念1.2、回溯法的效率1.3、回溯法问题分类1.4、回溯法的做题步骤二、经典问题2.1、组合问题2.1.1、77. 组合 - 值不重复2.1.2、216.组合总和III - 值不重复且等于目标值2.1.3、17. 电话号码的字母组合 - 双层回溯2.1.4、…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...
