【走迷宫】
题目

DFS代码
#include<bits/stdc++.h>
using namespace std;
const int N = 110;
int matrix[N][N];
int n, m;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
int dis[N][N];
void dfs(int x, int y, int cnt)
{if(cnt > dis[n-1][m-1]) return;if(x == n-1 && y == m-1) return;for(int i = 0; i < 4; i++){int nx = x + dx[i], ny = y + dy[i];if(nx < 0 || ny < 0 || nx >= n || ny >= m || matrix[nx][ny]) continue;if(dis[nx][ny] > dis[x][y] + 1){dis[nx][ny] = dis[x][y] + 1;dfs(nx, ny, cnt+1);}}
}
int main()
{scanf("%d%d", &n, &m);for(int i = 0; i < n; i++){for(int j = 0; j < m; j++){scanf("%d", &matrix[i][j]);}}memset(dis, 0x3f, sizeof dis); dis[0][0] = 0;dfs(0, 0, 0);cout << dis[n-1][m-1];return 0;
}优化:
1.if(cnt >= res) return; (较好)
2.if(dis[x][y] < cnt) return; (较好)
else dis[x][y] = cnt;
3. if(dis[nx][ny] > dis[x][y] + 1) (非常好)
{
dis[nx][ny] = dis[x][y] + 1;
dfs(nx, ny, cnt+1);
}
优化1+优化2都不如单用优化3
优化3可以替代优化2,同时可以不需要visited访问数组、cnt参数、res。
优化1可以和优化3搭配(需要cnt参数),效果最好,比单用优化3快一倍。为什么?
注意:优化2中和优化3中均不能加等号,前者会导致错误,后者会TLE。为什么?
BFS代码
#include<bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
#define f first
#define s secondconst int N = 110;
int g[N][N];
int n, m;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
int dis[N][N];
int bfs(int a, int b)
{queue<PII> q;q.push({a,b});dis[a][b] = 0;while(q.size()){PII u = q.front();q.pop();for(int i = 0; i < 4; i++){int nx = u.f + dx[i], ny = u.s + dy[i];if(nx >= 0 && ny >= 0 && nx < n && ny < m && !g[nx][ny] && dis[nx][ny] == -1){q.push({nx, ny});dis[nx][ny] = dis[u.f][u.s] + 1;}}}return dis[n-1][m-1];
}
int main()
{scanf("%d%d", &n, &m);for(int i = 0; i < n; i++){for(int j = 0; j < m; j++){scanf("%d", &g[i][j]);}}memset(dis, -1, sizeof dis);cout << bfs(0, 0);return 0;
}数组实现
#include<bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
#define f first
#define s secondconst int N = 110;
int g[N][N];
PII q[N * N];
int n, m;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
int dis[N][N];
int bfs(int a, int b)
{int h = 0, t = 0;q[0] = {a, b};dis[a][b] = 0;while(h <= t){auto u = q[h++];for(int i = 0; i < 4; i++){int nx = u.f + dx[i], ny = u.s + dy[i];if(nx >= 0 && ny >= 0 && nx < n && ny < m && !g[nx][ny] && dis[nx][ny] == -1){q[++t] = {nx, ny};dis[nx][ny] = dis[u.f][u.s] + 1;}}}return dis[n-1][m-1];
}
int main()
{scanf("%d%d", &n, &m);for(int i = 0; i < n; i++){for(int j = 0; j < m; j++){scanf("%d", &g[i][j]);}}memset(dis, -1, sizeof dis);cout << bfs(0, 0);return 0;
}
相关文章:

【走迷宫】
题目 DFS代码 #include<bits/stdc.h> using namespace std; const int N 110; int matrix[N][N]; int n, m; int dx[4] {-1, 0, 1, 0}, dy[4] {0, 1, 0, -1}; int dis[N][N]; void dfs(int x, int y, int cnt) {if(cnt > dis[n-1][m-1]) return;if(x n-1 &&a…...
迁移var数据到已分配逻辑卷的物理盘)
linux(debian)迁移var数据到已分配逻辑卷的物理盘
文章目录 0 背景1 查看当前情况1.1 查看磁盘空间1.2 列出所有可用块设备的信息,而且还能显示他们之间的依赖关系1.3 查看可用磁盘1.4 查看卷组 2 卷组中创建逻辑卷3 创建文件系统4 创建临时文件夹并挂载,然后备份源文件5 修改开机挂载配置5.1 查看原配置…...

【产品那些事】什么是应用程序安全态势管理(ASPM)?
文章目录 前言当前应用安全(AppSec)推进遇到的问题关于ASPM的定义 为什么需要ASPM:B端客户核心需求ASPM产品关键策略理想状态下的ASPMASPM与CSPM的区别国内外产品参考 前言 随着现代软件开发实践的快速演变,特别是在敏捷开发和 DevOps 的推动下…...

cocosUI多分辨率适配
需求:由于各个设备的分辨率和尺寸并不一样,所以需要一套适配系统去很好的针对不同的设备分辨率或尺寸进行适配,以给玩家一个很好的游戏体验。 目前的主流适配方案 目前,针对不同设备的适配,主流的方案通常包括以下几种…...

无法加载到主类
说明:记录一次项目启动错误,如下: 错误信息:错误: 找不到或无法加载主类 com.hezy.App 原因: java.lang.ClassNotFoundException: com.hezy.App 解决:首先,在项目中勾选这个,显示target文件夹 …...

深入理解Kafka核心设计与实践原理_03
深入理解Kafka核心设计与实践原理_03 03_消费者3.1消费者与消费者组3.2客户端开发3.2.1 必要的参数配置3.2.2 订阅主题与分区 草稿 03_消费者 与生产者对应的是消费者,应用程序可以通过KafkaConsumer来订阅主题,并从订阅的主题中拉取消息。不过在使用Ka…...

MySQL- 覆盖索引
覆盖索引(Covering Index)是 MySQL 中的一种优化技术,它能够显著提高查询性能。在使用覆盖索引的情况下,查询操作只需要访问索引即可获取所需的数据,而不必再访问表的实际数据行(即不需要回表)。…...

JSON与EXL文件互转
功能:实现json到excel文件的相互转换(支持json多选版) 目的:编码与语言对应,方便大家使用 页面设计: 介绍: 1.选择文件栏目选择想要转换的文件 2.生成路径是转换后文件所在目录 3.小方框勾选与不勾选分别代表exl到…...

后台管理权限自定义按钮指令v-hasPermi
第一步:在src下面建立一个自定义指令文件,放自定义指令方法 permission.js文件: /*** v-hasPermi 操作权限处理*/import store from "/store";export default {inserted(el, binding) {const { value } binding;//从仓库里面获取到后台给的数组const permission s…...

【Python绘制散点图并添加趋势线和公式以及相关系数和RMSE】
在Python中,绘制散点图并添加趋势线(通常是线性回归线)、公式、以及相关系数(Pearson Correlation Coefficient)和均方根误差(RMSE)可以通过结合matplotlib用于绘图,numpy用于数学运…...

linux bridge VLAN
TP-Link 支持 Linux 桥接(bridge)和 VLAN 功能的产品主要包括其高端的交换机和一些企业级路由器: TP-Link JetStream 系列交换机: TL-SG3424: 24端口千兆交换机,支持 VLAN 和桥接。TL-SG3210: 24端口千兆管理型交换机&…...

Java进阶篇之深入理解多态的概念与应用
引言 在Java面向对象编程(OOP)中,多态(Polymorphism)是一个关键概念,它允许相同类型的对象在不同的场景中表现出不同的行为。多态不仅增强了代码的灵活性和可扩展性,还极大地提高了代码的可维护…...

Linux下的进程调度队列
我们在进程那一篇讲到了操作系统时间片轮换调度的概念 那么Linux下具体是怎么调度的?...

统计回归与Matlab软件实现上(一元多元线性回归模型)
引言 关于数学建模的基本方法 机理驱动 由于客观事物内部规律的复杂及人们认识程度的限制,无法得到内在因果关系,建立合乎机理规律的数学模型数据驱动 直接从数据出发,找到隐含在数据背后的最佳模型,是数学模型建立的另一大思路…...
【项目】基于Vue3.2+ElementUI Plus+Vite 通用后台管理系统
构建项目 环境配置 全局安装vue脚手架 npm install -g vue/cli-init打开脚手架图形化界面 vue ui创建项目 在图形化界面创建项目根据要求填写项目相关信息选择手动配置勾选配置项目选择配置项目然后我们就搭建完成啦🥳,构建可能需要一点时间࿰…...

随机生成 UUID
1、随机生成 UUID主方法 /*** 随机生成 UUID* param {*} len 生成字符串的长度* param {*} radix 生成随机字符串的长度**/export function uuid_(len 30, radix 20) {var chars 0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz.split()var uuid [],ir…...
报名表EXCEL图片批量下载源码-CyberWinApp-SAAS 本地化及未来之窗行业应用跨平台架构
每次报名表都会包含大量照片,一张一张下载很慢 可以通过未来之窗开源平台架构 开开excel批量下载 实现代码也很简单 function 未来之窗下载(){ let 未来之窗地址 document.getElementById("batchurl").value; let 保存路径 document.getElementById(…...
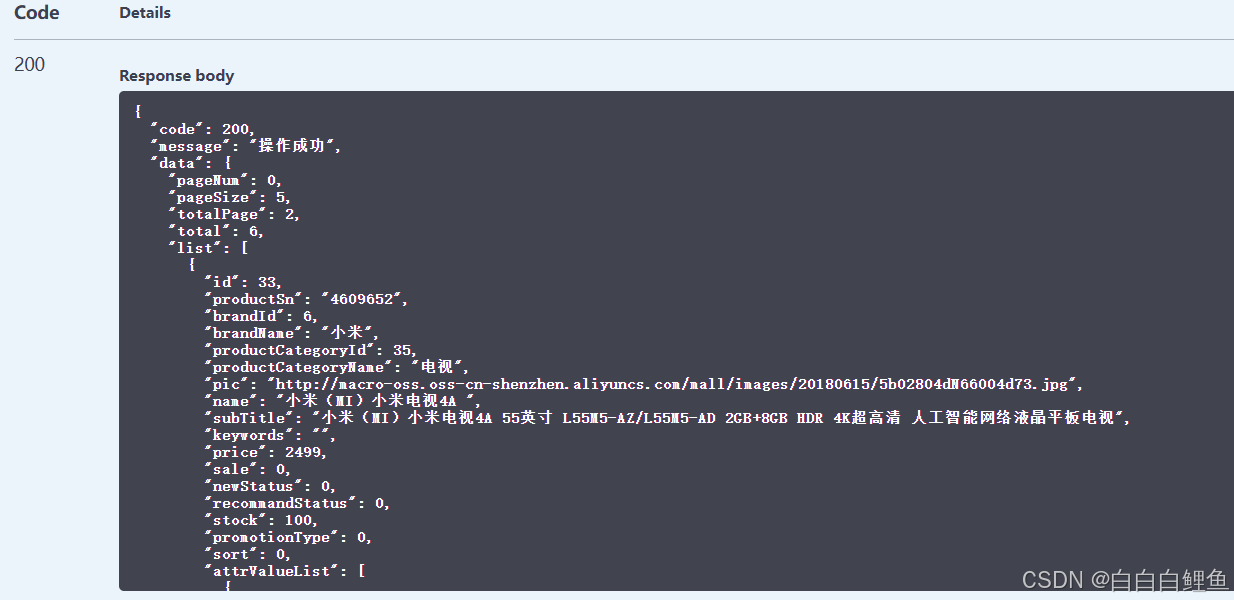
SpringBoot 整合 Elasticsearch 实现商品搜索
一、Spring Data Elasticsearch Spring Data Elasticsearch 简介 Spring Data Elasticsearch是Spring提供的一种以Spring Data风格来操作数据存储的方式,它可以避免编写大量的样板代码。 常用注解 常用注解说明如下: 注解名称 作用 参数说明 Docu…...

计算机毕业设计 助农产品采购平台 Java+SpringBoot+Vue 前后端分离 文档报告 代码讲解 安装调试
🍊作者:计算机编程-吉哥 🍊简介:专业从事JavaWeb程序开发,微信小程序开发,定制化项目、 源码、代码讲解、文档撰写、ppt制作。做自己喜欢的事,生活就是快乐的。 🍊心愿:点…...
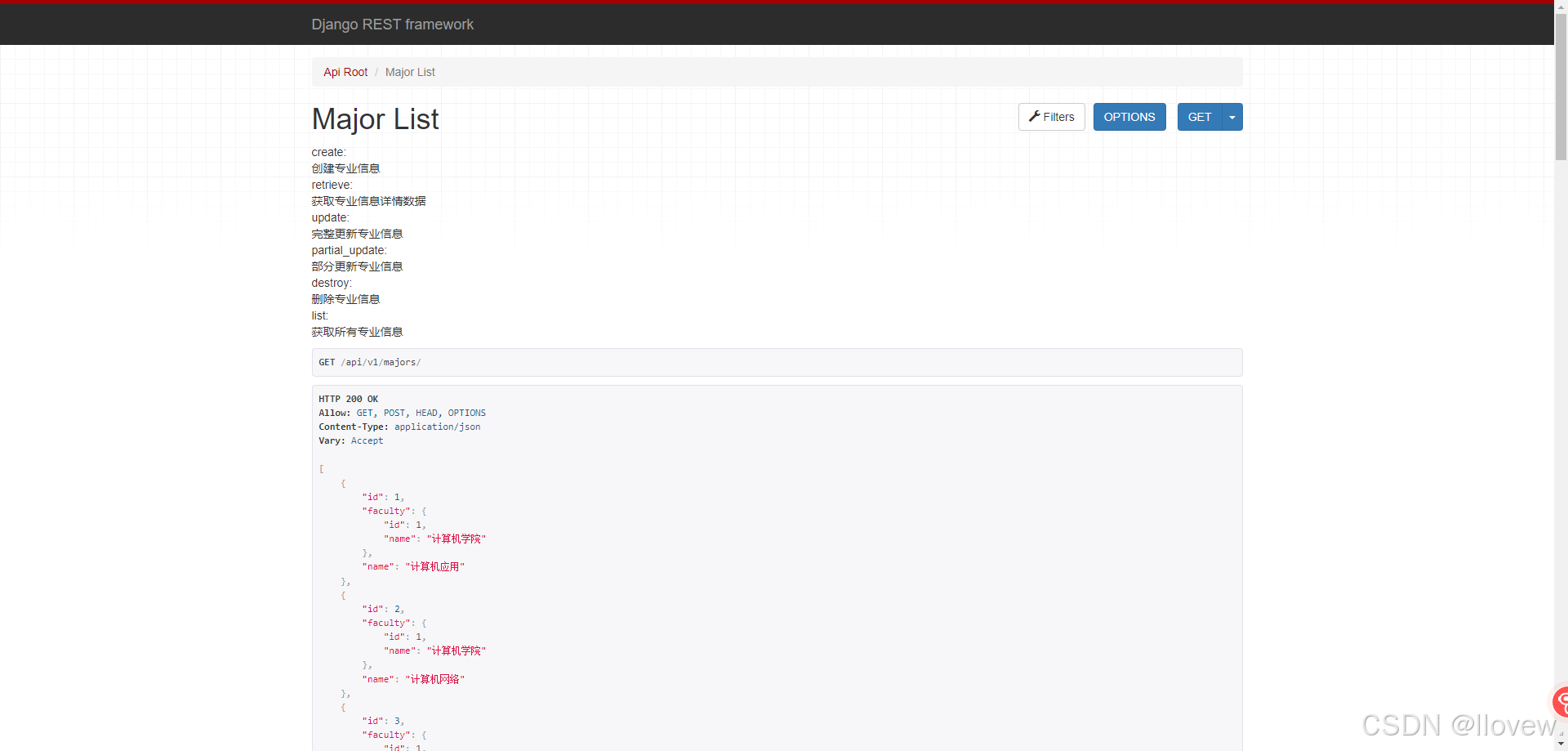
Django后台数据获取展示
续接Django REST Framework,使用Vite构建Vue3的前端项目 1.跨域获取后台接口并展示 安装Axios npm install axios --save 前端查看后端所有定义的接口 // 访问后端定义的可视化Api接口文档 http://ip:8000/docs/ // 定义的学生类信息 http://ip:8000/api/v1…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...
