P2801 教主的魔法
[题目通道](教主的魔法 - 洛谷)
摘要
分块,是一种优雅的暴力,它通过对数列分段,完成对数列一些区间操作和区间查询的操作,是一种根号算法。
这篇学习笔记&题解是本萌新在学习分块过程中的一些感悟,希望能够帮助分块零基础的同学学会基础分块。
0 说明
本文中,以下变量有特定的含义:
- blockblock:块的大小
- nn:被分块的数列的大小(长度)
- LxLx:第 xx 号块的左边界
- RxRx:第 xx 号块的右边界
- tottot:块的数量
- belongxbelongx:第 xx 号元素所属的块
在写作时,由于本萌新的失误,只好提前在这里令 [l,r][l,r] 与 [x,y][x,y] 等价。
1 建块
1.1 建块需要完成的任务
在读入数据后,建块需要完成以下几个任务:
- 确定块的大小
- 确定块的数量
- 标记每个块的左右边界
- 标记每个元素所属的块
- 对每个块的数据进行初始化
1.2 确定块的大小
一般来说,我们习惯于令 block=nblock=n。
但是由于毒瘤良心命题人泛滥,block=nblock=n 极其有可能被针对,在这种情况下,我们可以对块的大小适当作出一些调整,例如 n+1n+1,n−1n−1,nlg(n)lg(n)n 等。
一般这个工作只有一句话:
block = (int)sqrt((double)n);
1.3 确定块的数量
在确定了块的大小后,块的数目就很容易确定了。
但是 nn 不一定是一个完全平方数,我们需要把最后几个无法凑足 blockblock 个元素的再单独分一个块。
代码如下:
tot = n / block;
if(n % block) tot++;
1.4 标记每个块的左右边界
非常显然,L1=1,R1=block,L2=block+1,R2=2×block,⋯L1=1,R1=block,L2=block+1,R2=2×block,⋯
从而可以得出结论:
Lx=(x−1)⋅block+1,Rx=x⋅blockLx=(x−1)⋅block+1,Rx=x⋅block
特别地,Rtot=nRtot=n
代码:
for(int i = 1; i <= tot; i++){L[i] = (i - 1) * block + 1;R[i] = i * block;
}
R[tot] = n;
1.5 标记每个元素所属的块
根据 1.4,我们很容易推出公式如下:
belongx=x−1block+1belongx=blockx−1+1
代码如下:
for(int i = 1; i <= n; i++)belong[i] = (i - 1) / block + 1;
重要:在使用分块过程中,一定要注意区分 tottot 和 nn。 tottot 是块的总数,nn 是原来元素的总数。
1.6 对每个块的元素进行初始化
这项工作因题目不同而不同,如【教主的魔法】一题,就要对每个块的元素进行排序。
因为排序会对原始数列作出改变,所以在本题中,应当先把数列复制一遍再进行分块
2 分块题常见的操作
修改:
- 对数列 [l,r][l,r] 内的每个数加上 kk
- 对数列 [l,r][l,r] 内的每个数减去 kk
- etc.
查询:
- 求数列 [l,r][l,r] 内的所有数的和
- 求数列 [l,r][l,r] 内的数有多少大于/小于/大于等于/小于等于 kk
- etc.
3 修改操作
考虑两种修改操作本质相同,第二种修改操作相当于第一种修改操作中 k=−k′k=−k′。
3.1 暴力修改
考虑枚举区间 [l,r][l,r] 之间所有数,直接对其实施修改,在修改的过程中维护每一个块的和/大小关系等。
但这不是我们考虑的东西
3.2 考虑线段树思想
线段树一个重要思想:lazytag
考虑应用在分块中。在修改操作中,如果是整块,就不维护每个的具体信息,而是在这个块的 lazylazy 标记上加上 kk。对于没有整块修改的部分(即块 belongxbelongx 和 belongybelongy 的修改部分),暴力修改。
这样的话,第 ii 个数据 aiai 的真正数据值为 ai+lazybelongiai+lazybelongi。
如果询问涉及到排序,块 belongxbelongx 和 belongybelongy 需要全部重新备份和排序,对于块 [belongx+1,belongy−1][belongx+1,belongy−1] 的块,数的相对大小不会改变,所以可以不重新排序。
特别地,需要特判 belongx=belongybelongx=belongy 的情况。
代码:
void change(){if(belong[x] == belong[y]){for(int i = x; i <= y; i++){a[i] += k;sum[belong[x]] += k;}return;}for(int i = x; i <= R[belong[x]]; i++){a[i] += k;sum[belong[x]] += k;}for(int i = L[belong[y]]; i <= y; i++){a[i] += k; sum[belong[y]] += k;}for(int i = belong[x] + 1; i <= belong[y] - 1; i++){lazy[i] += k;sum[i] += blo * k;}
}
对以下这句代码作出特别解释:
sum[i] += blo * k;
不用特判最后一块的原因是:如果操作区间覆盖到的最后一块,也一定是作为 belongybelongy 处理掉了,剩下来的块长一定是 blockblock。
4 查询操作
4.1 查询元素和
对于块 belongxbelongx 和 belongybelongy,暴力枚举加和,注意加上其元素后还要加上 lazybelongilazybelongi
对于 [belongx+1,belongy−1][belongx+1,belongy−1] 的块,直接 ans=ans+sum[i] 即可。
同样的,需要特判 belongx=belongybelongx=belongy
代码:
int query_sum(){int ans = 0;if(belong[x] == belong[y]){for(int i = x; i <= y; i++){ans += a[i] + lazy[belong[x]];}return ans;}for(int i = x; i <= R[belong[x]]; i++){ans += a[i] + lazy[belong[x]];}for(int i = L[belong[x]]; i <= y; i++){ans += a[i] + lazy[belong[y]];}for(int i = belong[x] + 1; i <= belong[y] - 1; i++){ans += sum[i];}return ans;
}
4.2 查询关系
与4.1类似,在块 belongxbelongx 和 belongybelongy,暴力枚举求答案;
对于 [belongx+1,belongy−1][belongx+1,belongy−1] 的块,因为其是有序的,进行二分找到端点位置,然后加加减减求出块中有多少符合要求的元素即可。
本处代码见5.
5 教主的魔法
在学习完分块后,我们可以发现,教主的魔法就是一道裸的分块题。
因此,完整代码如下:
#include<bits/stdc++.h>
#include<vector>
using namespace std;
int m,n,t,pos[1251000];
int s[2151000],flag[1251000];
vector<int>v[550000];void reset(int x) {v[pos[x]].clear();for(int i=(pos[x]-1)*m+1; i<=min(pos[x]*m,n); i++)v[pos[x]].push_back(s[i]);sort(v[pos[x]].begin(),v[pos[x]].end());
}void change(int a,int b,int c) {for(int i=a; i<=min(pos[a]*m,b); i++)s[i]+=c;reset(a);if(pos[a]!=pos[b]) {for(int i=(pos[b]-1)*m+1; i<=b; i++)s[i]+=c;reset(b);}for(int i=pos[a]+1; i<=pos[b]-1; i++)flag[i]+=c;
}int query(int l,int r,int c) {int ans=0;for(int i=l; i<=min(pos[l]*m,r); i++)if(s[i]+flag[pos[l]]<c)ans++;if(pos[l]!=pos[r]) {for(int i=(pos[r]-1)*m+1; i<=r; i++)if(s[i]+flag[pos[r]]<c)ans++;}for(int i=pos[l]+1; i<=pos[r]-1; i++) {int x=c-flag[i];ans+=lower_bound(v[i].begin(),v[i].end(),x)-v[i].begin();}return ans;
}signed main() {scanf("%d %d",&n,&t);m=sqrt(n);for (int i=1; i<=n; i++) pos[i]=(i-1)/m+1;for (int i=1; i<=n; i++) scanf("%d",&s[i]);for(int i=1; i<=n; i++)pos[i]=(i-1)/m+1,v[pos[i]].push_back(s[i]);for(int i=1; i<=pos[n]; i++)sort(v[i].begin(),v[i].end());for (int i=1; i<=t; i++) {int a,b,c;char x;cin>>x;scanf("%d%d%d",&a,&b,&c);if (x=='M') {change(a,b,c);} else if (x=='A') {cout<<b-a+1-query(a,b,c)<<endl;}}return 0;
}相关文章:

P2801 教主的魔法
[题目通道](教主的魔法 - 洛谷) 摘要 分块,是一种优雅的暴力,它通过对数列分段,完成对数列一些区间操作和区间查询的操作,是一种根号算法。 这篇学习笔记&题解是本萌新在学习分块过程中的一些感悟,希望能够帮助…...

Go 语言channel的应用场景及使用技巧
通过反映的方式执行 select 语句。这在处理有很多 case 子句,尤其是不定长 case 子句的情况时非常有用。 1. 使用反射操作 select 和 channel 使用 select 语句可以处理 chan 的 send 和 recv, send 和 recv 都可以作为 case 子句。如果需要同时处理两个 chan, 则可以写成下面…...

QLabel设置图像的方法+绘制文本换行显示
1、QLabel设置图像有两种方法 (1) void setPicture(const QPicture &); (2) void setPixmap(const QPixmap &); QPicture和QPixmap都是继承于QPaintDevice,它们都可以通过加载图片的方式获取:bool load(QIODevice *dev, const char *format …...

LVS原理及相关配置
1. 描述以及工作原理 1. 什么是 LVS linux virtural server 的简称,也就是 linxu 虚拟机服务器,这是一个 由章文嵩博士发起的开源项目,官网是 http://www.linuxvirtualserver.org,现在 lvs 已经是 linux 内核标 准的一部分,使用…...

webrtc一对一视频通话功能实现
项目效果 实现原理 关于原理我就不做说明,直接看图 WebRTC建立的时序图 系统用例逻辑 搭建环境 turn服务器:Ubuntu24.04搭建turn服务器 mkcert的安装和使用:配置https访问 必须使用https协议, 由于浏览器的安全策略导致的&am…...
传递数据的例子写一个)
通道(channel)传递数据的例子写一个
当然!以下是一个简单的 Go 程序示例,展示了如何使用通道(channel)在两个 goroutine 之间传递数据。示例代码 go package mainimport ("fmt""time" )// 发送数据到通道的 goroutine func sendData(ch chan int…...

Vue3+Echarts+饼图环形图
记得给容器宽高 <div id"leftChartguawang" style"height: 28vh"></div> 配置函数 const leftChartguawang () > {const chartBox echarts.init(document.getElementById(leftChartguawang))let datas [[{ name: 居民节能建筑, value…...

Python while编程题目|AI悦创Python一对一教学辅导
你好,我是悦创。 以下是十道有创意的while循环编程题目,每道题目都有一定的难度,适合锻炼编程逻辑和思维能力。 题目1:旋转字符串 描述:给定一个字符串,每次循环将字符串的第一个字符移到末尾࿰…...

C语言 | Leetcode C语言题解之第324题摆动排序II
题目: 题解: static inline void swap(int *a, int *b) {int c *a;*a *b;*b c; }static inline int partitionAroundPivot(int left, int right, int pivot, int *nums) {int pivotValue nums[pivot];int newPivot left;swap(&nums[pivot], &a…...

Docker③_VMware虚拟机和Docker的备份与恢复
目录 1. VMware虚拟机的快照备份 1.1 VMware本机的快照备份 1.2 VMware快照备份到另一电脑 2. Docker知识点 2.1 Docker镜像和容器的关系 2.2 Docker的存储卷 2.3 Docker命令简介 2.4 删除Anylink镜像 3. Docker备份和恢复 3.1 确定要回滚的容器和版本 3.2 备份当前…...

【EMC专题】ESD抑制器简要介绍
在ESD保护器件中可以分为陶瓷基类型和半导体基类型。其中有一类陶瓷基类型,使用的机制是电极间放电方法的产品就是ESD抑制器。本文章简要介绍了ESD抑制器的特点、基本结构和特性。 ESD抑制器的特点 ESD抑制器是间隙型的ESD(静电放电 Electrostatic Discharge)对策保护元件,…...

贷齐乐系统最新版SQL注入(绕过WAF可union select跨表查询)
目录 标题:贷齐乐系统最新版SQL注入(绕过WAF可union select跨表查询) 内容: 一,环境部署 二,源码分析 三,sql注入 总结: [回到顶部](#article_top) 一&am…...

『大模型笔记』虚拟机(Virtual Machine,VM)与Docker对比!
『大模型笔记』虚拟机(Virtual Machine,VM)与Docker对比! 文章目录 一. 虚拟机(Virtual Machine,VM)与Docker对比!1. 定义这两种技术2. 工作原理3. 关于如何选择适合工作负载的技术的指导二. 参考文献Docker 只是一个轻量级的虚拟机吗?虽然二者确实有一个共同点,即 虚…...

基于SpringBoot+Vue框架的租车管理系统
文章目录 一、项目介绍二、项目类型三、技术栈介绍1.客户端技术栈2.服务端技术栈 四、项目创新点五、项目功能介绍1.客户端功能2.服务端功能 六、项目的主要截图页面如下展示1.客户端展示2.服务端展示 七、项目源码 一、项目介绍 大家好,我是执手天涯,…...

HAProxy基本配置及参数实操
目录 编辑什么是负载均衡 为什么用负载均衡 四层和七层的区别 实验环境 实验步骤 webserver上安装nginx 启动nginx 安装haproxy 编辑配置文件 多进程 多线程 SORRY SERVER 访问重定向 maxconne最大可承受连接 socat 工具 常用示例 ha p r ox y 的 算 法 静 …...

go-zero中间件的使用
一、自定义中间件 1、在api中在服务中定义一个中间件,名字随便取 type PostDemoReq {Name string json:"name" validate:"required" // 姓名Age int64 json:"age" validate:"required,gte1,lte130" // 年龄// optional 表示可选,omi…...

六、ESP32-S3上使用MicroPython点亮WS2812智能LED灯珠并通过web控制改变灯珠颜色优化超时和线程
实现通过ESP32S3连接Wi-Fi并使用Web页面控制WS2812灯珠的颜色,可以使用ESP32的WebServer库来创建一个简单的Web界面。通过这个界面,可以动态地控制灯珠的显示效果。 针对 五、ESP32-S3上使用MicroPython点亮WS2812智能LED灯珠并通过web控制改变灯珠颜色…...
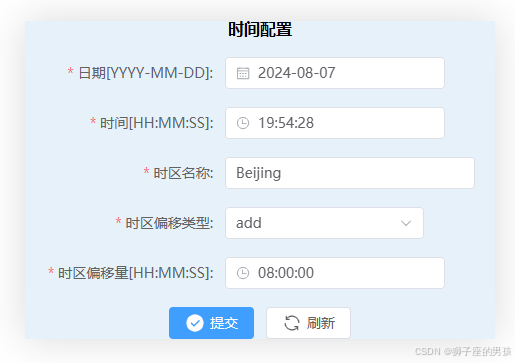
(el-Time-Picker)操作(不使用 ts):Element-plus 中 TimePicker 组件的使用及输出想要时间格式需求的解决过程
Ⅰ、Element-plus 提供的 TimePicker 时间选择器组件与想要目标情况的对比: 1、Element-plus 提供 TimePicker 组件情况: 其一、Element-ui 自提供的 TimePicker 代码情况为(示例的代码): // Element-plus 提供的组件代码: <template>…...
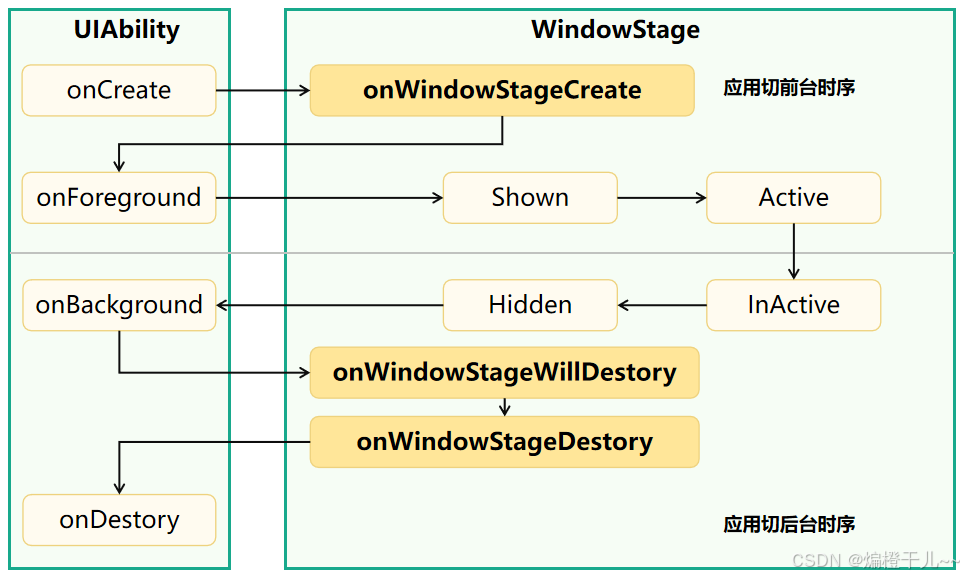
UIAbility组件基础(一)
一、概述 UIAbility组件是一种包含UI的应用组件,主要用于和用户交互。UIAbility组件是系统调度的基本单元,为应用提供绘制界面的窗口。一个应用可以包含一个或多个UIAbility组件。每一个UIAbility组件实例都会在最近任务列表中显示一个对应的任务。 U…...

神经网络的数学原理
前言:Hello大家好,我是小哥谈。人工智能技术的发展与成功应用已经成为21世纪科技领域最大的新现象。然而,科学地理解人工智能原理已经超出了现有科学体系的范畴。显然,人工智能是人类科学技术发展的必然结果,人工智能科学也将是人类科学进步与发展必然实现的目标🌈 …...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

jdbc查询mysql数据库时,出现id顺序错误的情况
我在repository中的查询语句如下所示,即传入一个List<intager>的数据,返回这些id的问题列表。但是由于数据库查询时ID列表的顺序与预期不一致,会导致返回的id是从小到大排列的,但我不希望这样。 Query("SELECT NEW com…...

【笔记】AI Agent 项目 SUNA 部署 之 Docker 构建记录
#工作记录 构建过程记录 Microsoft Windows [Version 10.0.27871.1000] (c) Microsoft Corporation. All rights reserved.(suna-py3.12) F:\PythonProjects\suna>python setup.py --admin███████╗██╗ ██╗███╗ ██╗ █████╗ ██╔════╝…...

【题解-洛谷】P10480 可达性统计
题目:P10480 可达性统计 题目描述 给定一张 N N N 个点 M M M 条边的有向无环图,分别统计从每个点出发能够到达的点的数量。 输入格式 第一行两个整数 N , M N,M N,M,接下来 M M M 行每行两个整数 x , y x,y x,y,表示从 …...

java+webstock
maven依赖 <dependency><groupId>org.java-websocket</groupId><artifactId>Java-WebSocket</artifactId><version>1.3.5</version></dependency><dependency><groupId>org.apache.tomcat.websocket</groupId&…...
