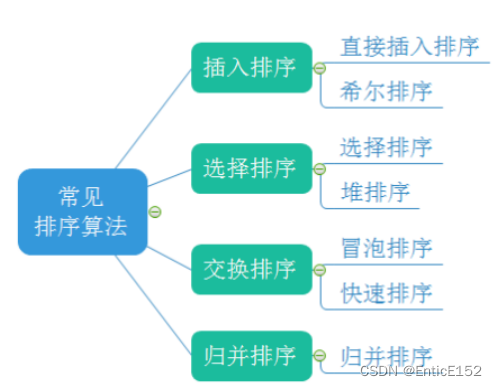
[数据结构]排序算法
目录
常用排序算法的实现::
1.排序的概念及其运用
2.插入排序
3.希尔排序
4.选择排序
5.冒泡排序
6.堆排序
7.快速排序
8.归并排序
9.排序算法复杂度及稳定性分析
10.排序选择题练习
常用排序算法的实现::
1.排序的概念及其运用
排序:所谓排序,就是一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的,否则称之为不稳定。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。

测试排序的性能对比:
//测试排序的性能对比
void TestOP()
{srand(time(0));const int N = 100000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand();a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin3 = clock();SelectSort(a3, N);int end3 = clock();int begin4 = clock();HeapSort(a4, N);int end4 = clock();int begin5 = clock();QuickSort(a5, 0, N - 1);int end5 = clock();int begin6 = clock();MergeSort(a6, N);int end6 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);printf("SelectSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);printf("QuickSort:%d\n", end5 - begin5);printf("MergeSort:%d\n", end6 - begin6);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);
}2.插入排序
插入排序基本思想:
插入排序是一种简单的插入排序算法,其基本思想是:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列。
实际中我们玩扑克牌时,就用了插入排序的思想:

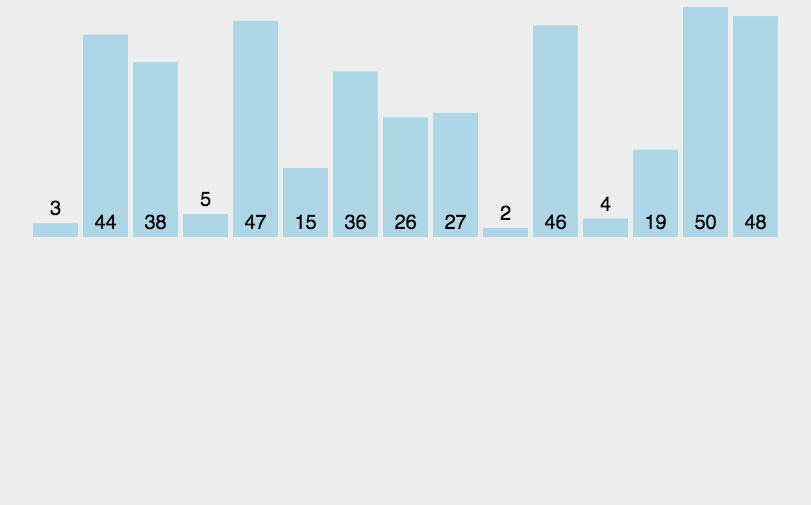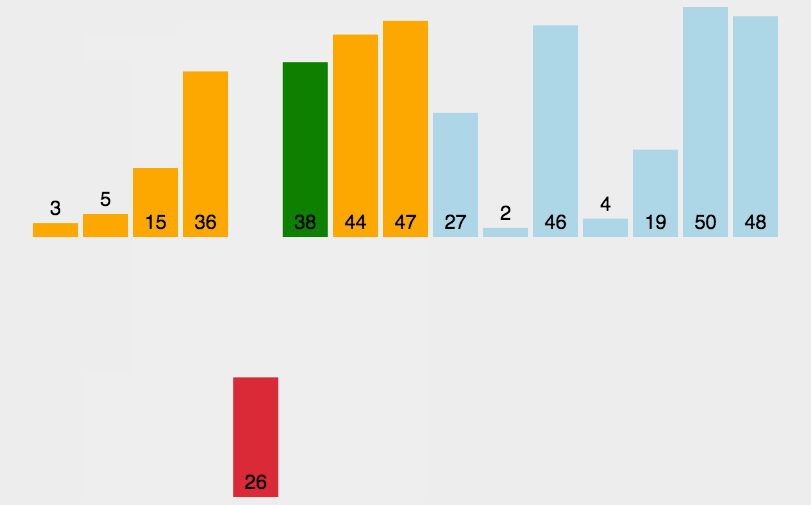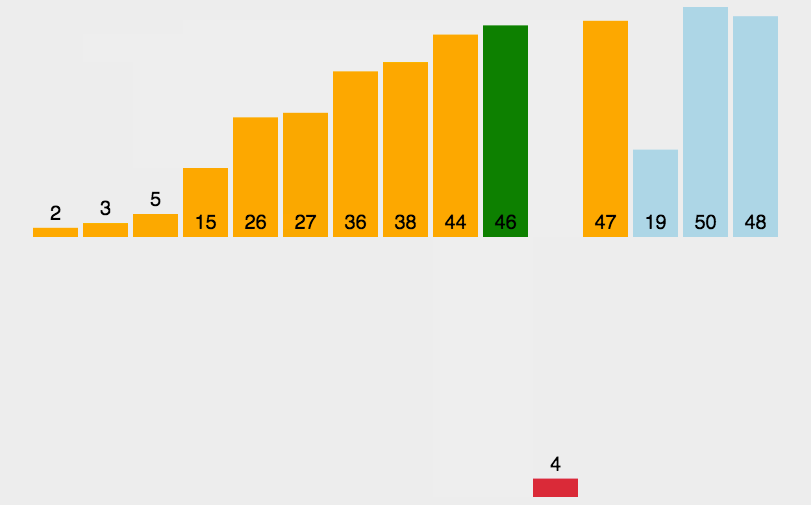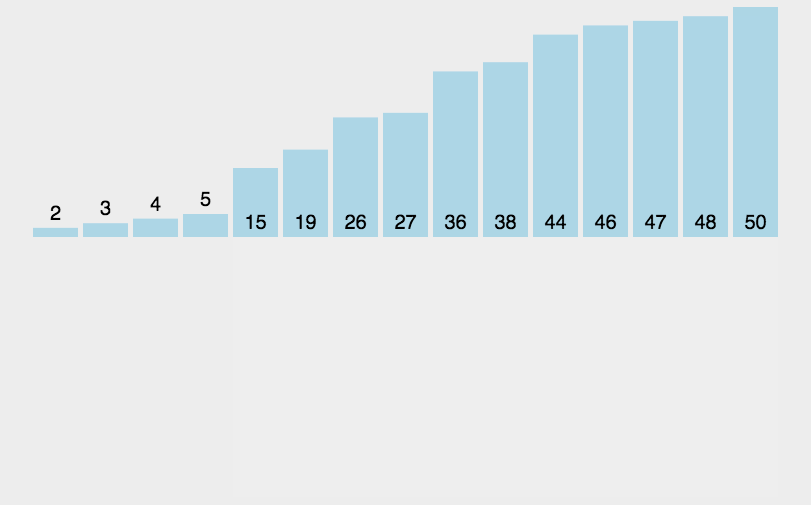
void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = a[end] + 1;while (end >= 0){if (a[end] > tmp){a[end + 1] = a[end];--end;}else{break;}}a[end + 1] = tmp;}
}3.希尔排序(缩小增量排序)
希尔排序的基本思想:
希尔排序又称缩小增量法,希尔排序的基本思想是:先选定一个整数,把待排序文件中所有记录分成各组,所有距离为gap的记录分在同一组内,并对每一组内的记录进行排序,然后重复上述分组和排序的工作。当达到gap=1时,所有记录在同一组内已排好序。
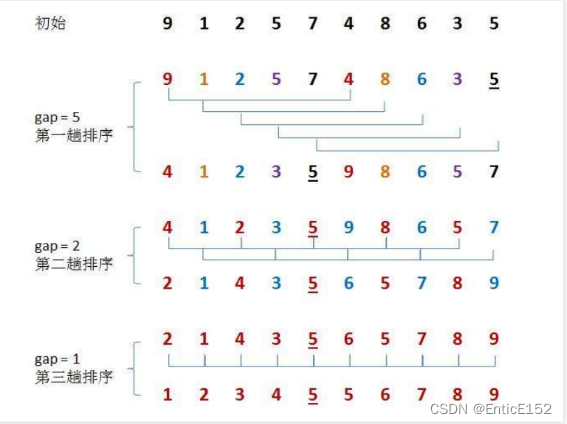
希尔排序的特性总结:
1.希尔排序是对插入排序的优化。
2.当gap>1时都是预排序,目的是让数组更接近有序。当gap==1时,数组已经接近有序了,这样就会很快,整体而言,可以达到优化的效果。
3.希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在很多书中给出的希尔排序的时间复杂度都不固定。


《数据结构-用面相对象方法与C++描述》--- 殷人昆

注:我们的gap是按照Knuth提出的方式取值的,而且Knuth进行了大量的实验统计,我们暂时就按照:O(n^1.25)到O(1.6*n^1.25)来算。
4.稳定性:不稳定
代码实现:
//希尔排序(缩小增量排序)
//希尔排序又称缩小增量法 希尔排序的基本思想是:先选定一个整数,把待排序文件中所有
//记录分成n个组 所有距离为的记录分在同一个组 并对每一组内的记录进行排序,然后取重复上述分组
//和排序的工作,当达到1时,所有记录在统一组内排好序
//希尔排序的时间复杂度为O(N^1.3) 数据量特别大时略逊于N*logN
void ShellSort(int* a, int n)
{//gap > 1预排序 gap == 1直接插入排序int gap = n;while (gap > 1){//gap = gap / 2;gap = gap / 3 + 1;for (int j = 0; j < gap; ++j){for (int i = j; i < n - gap; i += gap){//[0,end] 插入 end+gap [0,end+gap]有序——间隔为gap的数据int end = i;int tmp = a[end + gap];while (end >= 0){if (a[end] > tmp){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}}
}4.选择排序
选择排序的基本思想:
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
在元素集合array[i]—array[n-1]中选择关键码最大(小)的数据元素,若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素互换,在剩余的array[i]—array[n-2](array[i+1]—array[n-1])集合中,重复上述步骤,直到集合剩余一个元素。

选择排序的特性总结:
1.选择排序的代码非常好理解,但是效率不是很好,实际中很少用
2.时间复杂度:O(N^2)
3.空间复杂度:O(1)
4.稳定性:不稳定
代码实现:
//选择排序
//最坏时间复杂度:O(N^2)
//最好时间复杂度:O(N^2)
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
void SelectSort(int* a, int n)
{int begin - 0.end = n - 1;while (begin < end){//选出最小的放begin位置//选出最大的放end位置int mini = begin, maxi = begin;for (int i = begin + 1; i <= end; ++i){if (a[i] > a[maxi]){maxi = i;}if (a[i] < a[mini]){mini = i;}}Swap(&a[begin], &a[mini]);//最大数据在第一个位置时需要修正一下maxiif (maxi == begin)maxi = mini;Swap(&a[end], &a[maxi]);++begin;--end;}
}5.冒泡排序
基本思想:
所谓交换,就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置,冒泡排序的特点是:将键值较大的记录向序列的尾部移动,键值较小的数据向序列的前部移动。
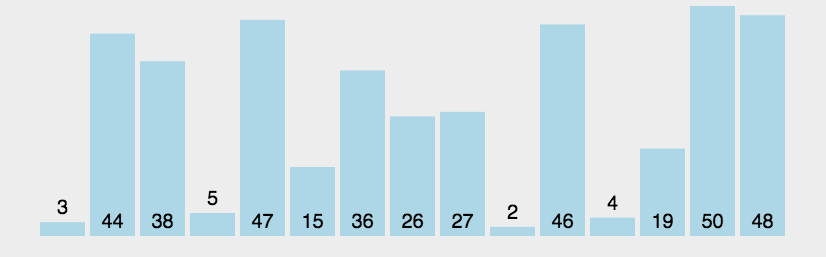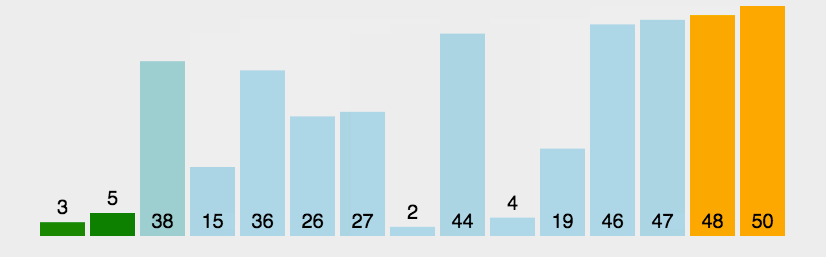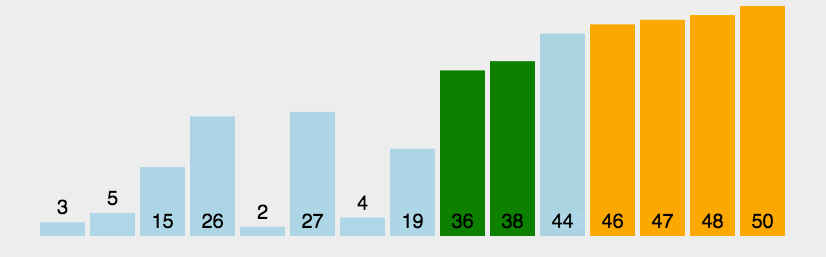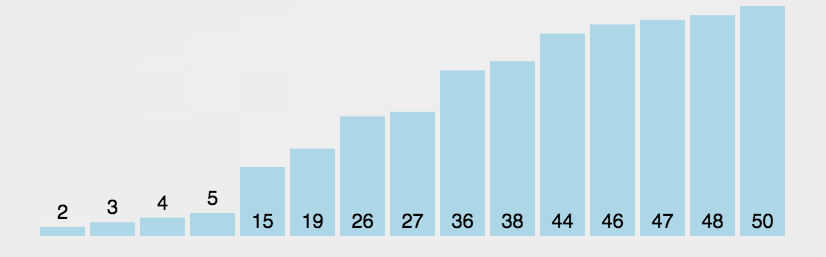
冒泡排序的特性总结:
1.时间复杂度:O(N^2)
2.空间复杂度:O(1)
3.稳定性:稳定
代码实现:
//冒泡排序
//最坏时间复杂度——O(N^2)
//最好时间复杂度——O(N)
void BubbleSort(int* a, int n)
{for (int j = 0; j < n; ++j){int exchange = 0;for (int i = 1; i < n - j; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0){break;}}
}6.堆排序
堆排序(HeapSort)是指利用堆这种数据结构所设计的一种排序算法,它是选择排序的一种,通过堆来进行选择数据,需要注意的是升序要建大堆,降序要建小堆。
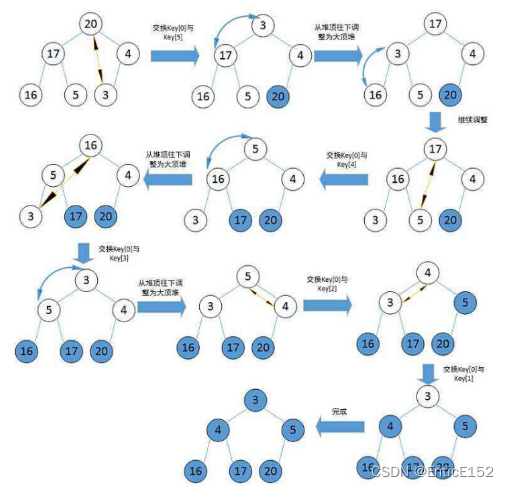
堆排序的特性总结:
1.堆排序使用堆来选数,效率就高了很多
2.时间复杂度:O(N*logN)
3.空间复杂度:O(1)
4.稳定性:不稳定
代码实现:
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
void AdjustDown(int* a, int n, int parent)
{int minChild = parent * 2 + 1;while (minChild < n){if (minChild + 1 < n && a[minChild + 1] > a[minChild]);{minChild++;}if (a[minChild] > a[parent]){Swap(&a[minChild], &a[parent]);parent = minChild;minChild = parent * 2 + 1;}else{break;}}
}
void HeapSort(int* a, int n)
{for (int i = (n - 1 - 1) / 2; i >= 0; --i){AdjustDown(a, n, i);}int i = 1;while (i < n){Swap(&a[0], &a[n - i]);AdjustDown(a, n - i, 0);++i;}
}7.快速排序
//假设按照升序对array数组中[left, right)区间中的元素进行排序
void QuickSort(int array[], int left, int right)
{if(right - left <= 1)return;// 按照基准值对array数组的 [left, right)区间中的元素进行划分int div = partion(array, left, right);// 划分成功后以div为边界形成了左右两部分 [left, div) 和 [div+1, right)// 递归排[left, div)QuickSort(array, left, div);// 递归排[div+1, right)QuickSort(array, div+1, right);
}//快速排序
//单趟排序:
//1.选1个key(一般是第一个或者是最后一个)
//2.单趟排序要求小的在key的左边,大的在key的右边
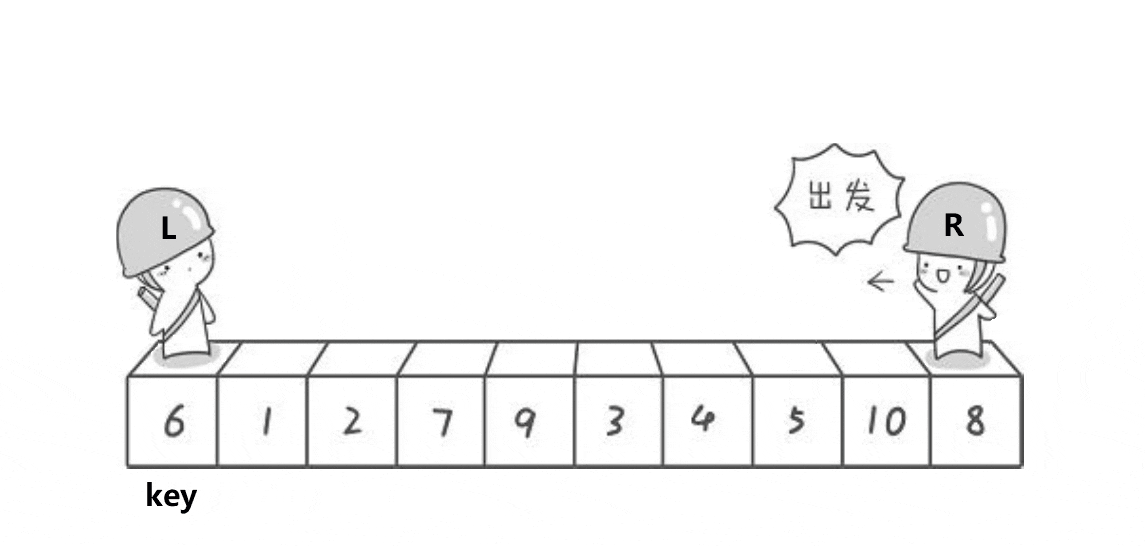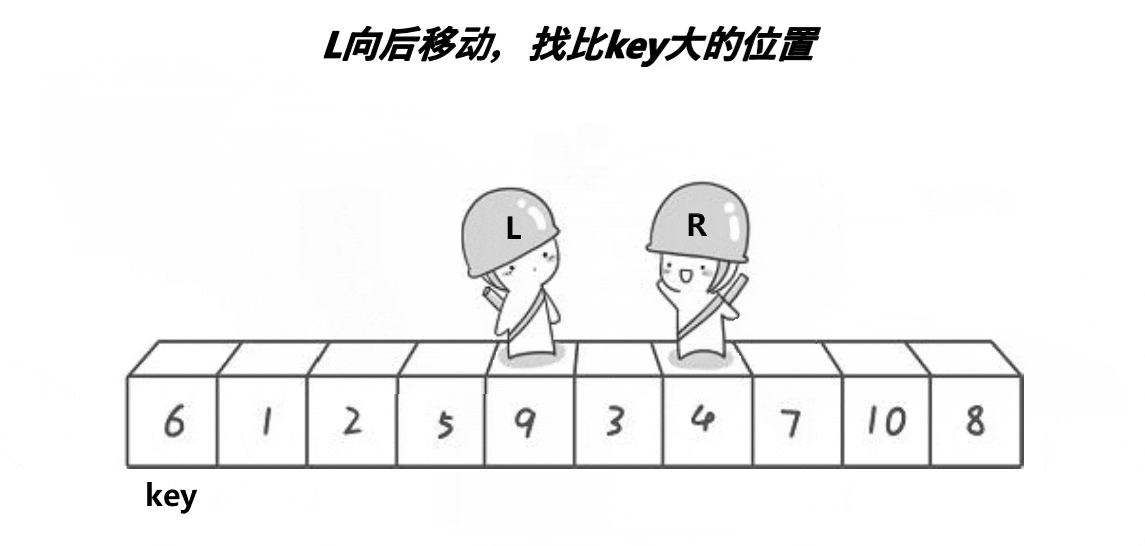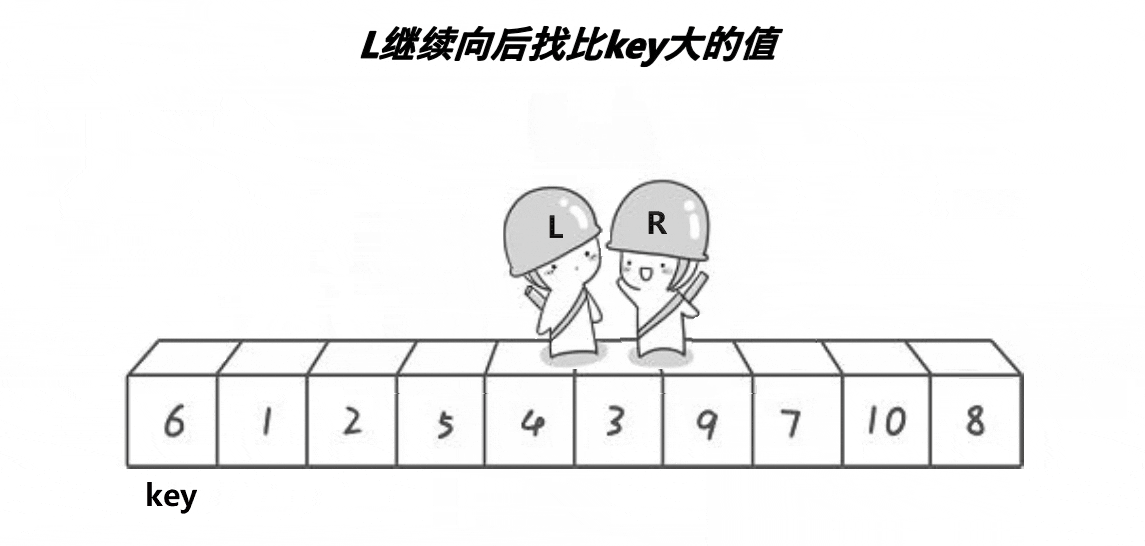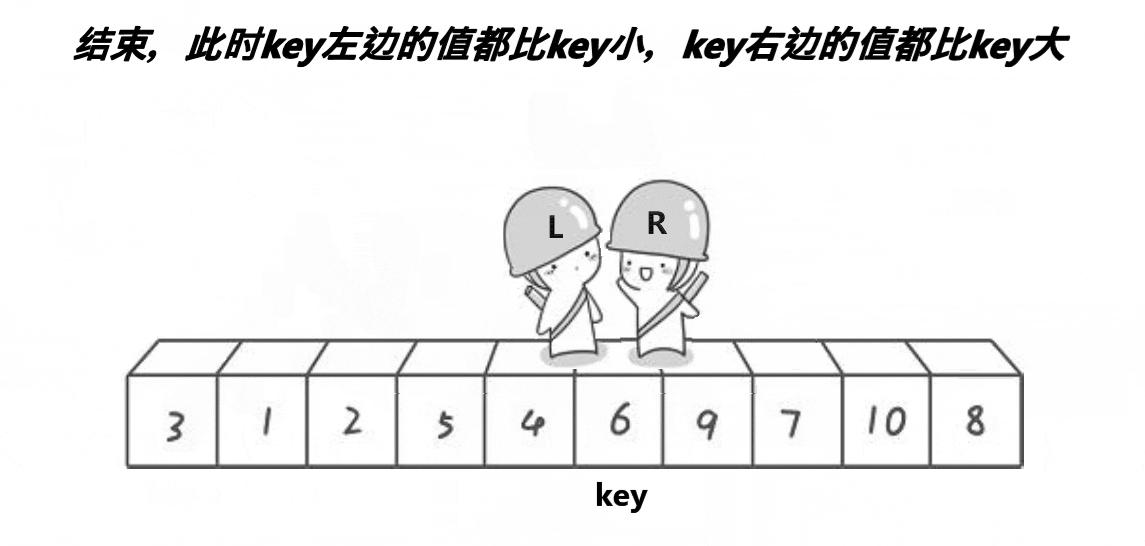
//相遇位置如何保证比key要小——左边第一个做key R先走
//1.R停下来 L遇到R 二者相遇 相遇位置比key小
//2.L停下来 R遇到L 二者相遇 相遇位置比key小
//发生第二种情况一定是R没有找到小的和L相遇,但此时L的位置已经被换成比key小的数据
//同样的道理:如果右边第一个做key——L先走
//单趟排序的价值
//1.key已经找到了它的最终位置,这个数已经排好了
//2.分割出去了两个子区间,如果子区间有序。整体就有序了
//子区间如何有序呢?——子区间递归
//最好时间复杂度:O(N*logN)
//最坏时间复杂度:O(N^2)
int PartSort(int* a, int left, int right)
{//数组之间的交换 不能和值换 要和对应的位置换int keyi = left;while (left < right){//R找小while (left < right && a[right] >= a[keyi]){--right;}//L找大while (left < right && a[left] <= a[keyi]){++left;}if(left < right)Swap(&a[left], &a[right]);}int meeti = left;Swap(&a[meeti], &a[keyi]);return meeti;
}Hoare版本
//优化快速排序:1.三数取中 2.小区间优化减少递归次数
//三数取中
int GetMidIndex(int* a, int left, int right)
{int mid = (right + left) / 2;if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] > a[right]){return left;}else{return right;}}else//a[left]>=a[mid]{if (a[mid] > a[right]){return mid;}else if (a[left] > a[right]){return left;}else{return right;}}
}
//Hoare
int PartSort1(int* a, int left, int right)
{//三数取中int mid = GetMidIndex(a, left, right);Swap(&a[left], &a[mid]);int keyi = left;while (left < right){//R找小while (left < right && a[right] >= a[keyi]){--right;}//L找大while (left < right && a[left] <= a[keyi]){++left;}if (left < right)Swap(&a[left], &a[right]);}int meeti = left;Swap(&a[meeti], &a[keyi]);return meeti;
}
//[begin,end]
void QuickSort(int* a, int begin, int end)
{if (begin >= end){return;}if (end - begin <= 8){InsertSort(a + begin, end - begin + 1);}else{int keyi = PartSort1(a, begin, end);//[begin,keyi-1] keyi [keyi+1,end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);}
}挖坑法

//挖坑法
//理解:1.左边是坑必然右边先走找数填坑 2.相遇位置必然是坑
int PartSort2(int* a, int left, int right)
{//三数取中int mid = GetMidIndex(a, left, right);Swap(&a[left], &a[mid]);int keyi = left;int key = a[left];int hole = left;while (left < right){//右边找小 填到左边的坑while (left < right && a[right] >= key){--right;}a[hole] = a[right];hole = right;//左边找大填到右边的坑while (left < right && a[left] <= key){++left;}a[hole] = a[left];hole = left;}a[hole] = key;return hole;
}
//[begin,end]
void QuickSort(int* a, int begin, int end)
{if (begin >= end){return;}if (end - begin <= 8){InsertSort(a + begin, end - begin + 1);}else{int keyi = PartSort2(a, begin, end);//[begin,keyi-1] keyi [keyi+1,end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);}
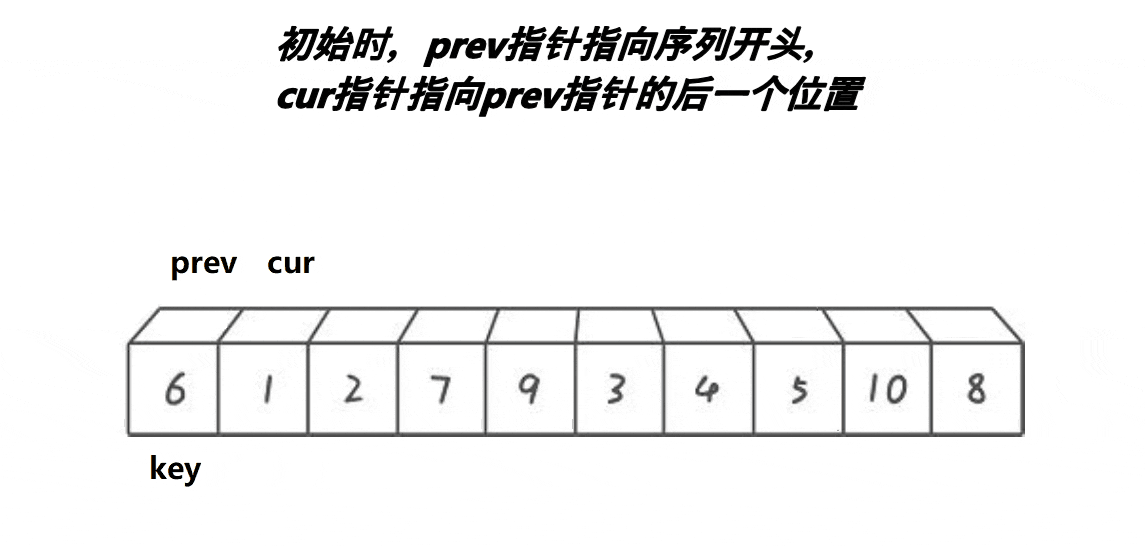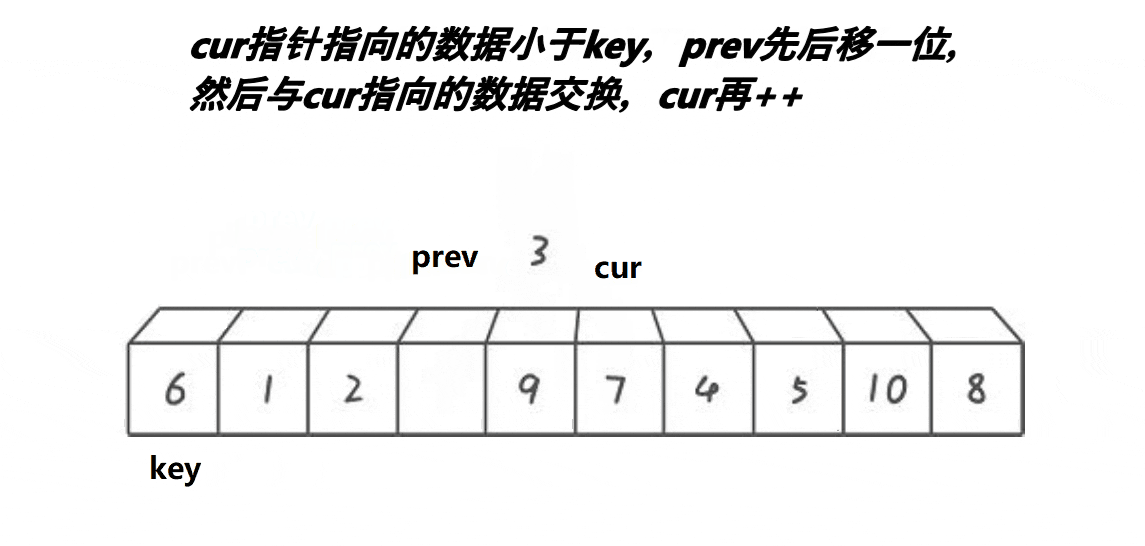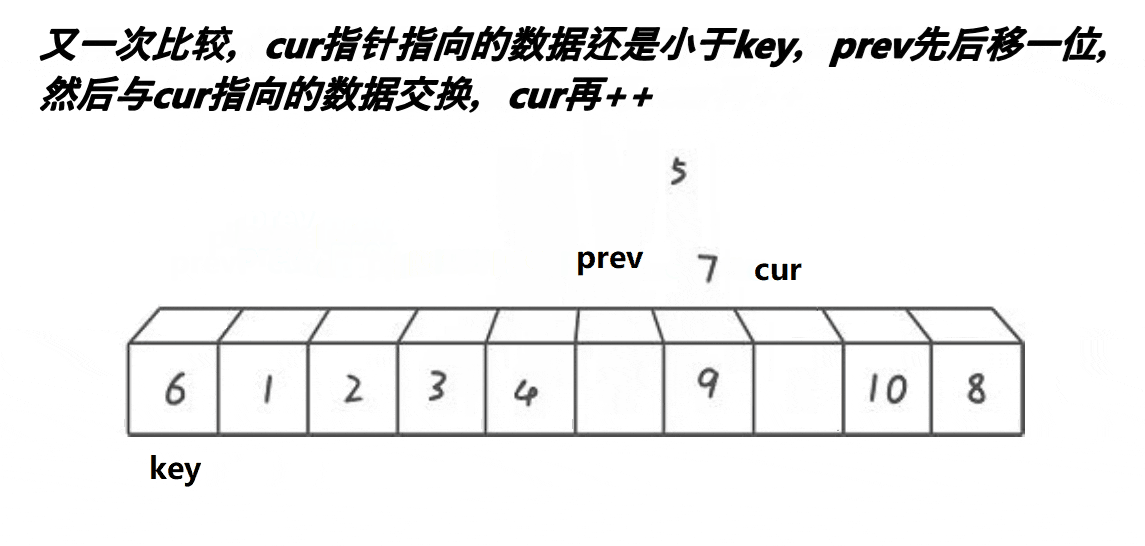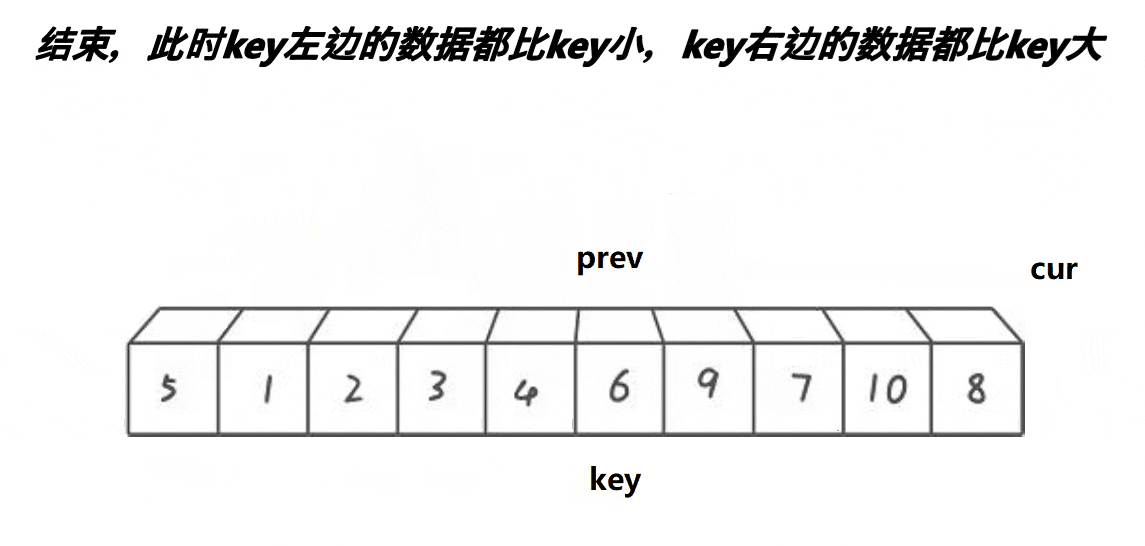
}前后指针法:
//前后指针法
//cur找小 prev紧跟着cur prev和cue之间间隔的是比key大的值
//cur遇到比key小的值时 就停下来 ++prev
//交换prev和cur位置的值
int PartSort3(int* a, int left, int right)
{//三数取中int mid = GetMidIndex(a, left, right);Swap(&a[left], &a[mid]);int keyi = left;int prev = left;int cur = left + 1;while (cur <= right){if (a[cur] < a[keyi] && ++prev != cur)Swap(&a[cur], &a[prev]);++cur;}//如果交换的是数组中的值 int key = a[left] Swap(&left,&a[prev])只是和局部变量key进行交换 并没有改变数组中的值Swap(&a[keyi], &a[prev]);return prev;
}
void QuickSort(int* a, int begin, int end)
{if (begin >= end){return;}if (end - begin <= 8){InsertSort(a + begin, end - begin + 1);}else{int keyi = PartSort3(a, begin, end);//[begin,keyi-1] keyi [keyi+1,end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);}
}快速排序非递归:
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
//静态栈
/*#define N 100
typedef int STDataType;
struct Stack
{STDataType a[N];int top;
};*/
//动态栈
typedef char STDataType;
typedef struct Stack
{STDataType * a;int top;int capacity;
}ST;
void StackInit(ST* ps);
void StackDestory(ST* ps);
void StackPush(ST* ps, STDataType x);
void StackPop(ST* ps);
bool StackEmpty(ST* ps);
int StackSize(ST* ps);
//访问栈顶数据
STDataType StackTop(ST* ps);
#include"Stack.h"
void StackInit(ST* ps)
{assert(ps);ps->a = NULL;ps->top = ps->capacity = 0;
}
void Destory(ST* ps)
{assert(ps);free(ps->a);ps->a = NULL;ps->capacity = ps->top = 0;
}
//数据结构建议不要直接访问结构体数据,一定要通过函数接口访问
//解耦:高内聚,低耦合
void StackPush(ST* ps, STDataType x)
{assert(ps);if (ps->top == ps->capacity){int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;STDataType* tmp = (STDataType*)realloc(ps->a, newCapacity * sizeof(STDataType));if (tmp == NULL){perror("realloc fail");exit(-1);}ps->a = tmp;ps->capacity = newCapacity;ps->a[ps->top] = x;ps->top++;}
}
void StackPop(ST* ps)
{assert(ps);assert(!StackEmpty(ps));--ps->top;
}
STDataType StackTop(ST* ps)
{assert(ps);//为空不能访问栈顶元素assert(!StackEmpty(ps));return ps->a[ps->top - 1];
}
bool StackEmpty(ST* ps)
{assert(ps);return ps->top == 0;
}
int StackSize(ST* ps)
{assert(ps);return ps->top;
}
#include"Stack.h"
//快速排序的非递归
//改非递归:递归函数中的栈帧保存什么 数据结构中的栈就保存什么
void QuickSortNonR(int* a, int begin, int end)
{ST st;StackInit(&st);StackPush(&st, begin);StackPush(&st, end);while (!StackEmpty(&st){int right = StackTop(&st);StackPop(&st);int left = StackTop(&st);StackPop(&st);if (left >= right){continue;}int keyi = PartSort3(a, left, right);//[left,keyi-1] l=keyi [keyi+1,right]StackPush(&st, keyi+1);StackPush(&st, right);StackPush(&st, left);StackPush(&st, keyi-1);}StackDestory(&st);
}
//优化:在区间为1或者区间不存在的时候 区间值不压入栈中
void QuickSortNonR(int* a, int begin, int end)
{ST st;StackInit(&st);StackPush(&st, begin);StackPush(&st, end);while (!StackEmpty(&st){int right = StackTop(&st);StackPop(&st);int left = StackTop(&st);StackPop(&st);int keyi = PartSort3(a, left, right);//[left,keyi-1] l=keyi [keyi+1,right]if (keyi + 1 < right){StackPush(&st, keyi + 1);StackPush(&st, right);}if (left < right - 1){StackPush(&st, left);StackPush(&st, keyi - 1);}}StackDestory(&st);
}快速排序的特性总结:
1.快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
2.时间复杂度:O(N*logN)
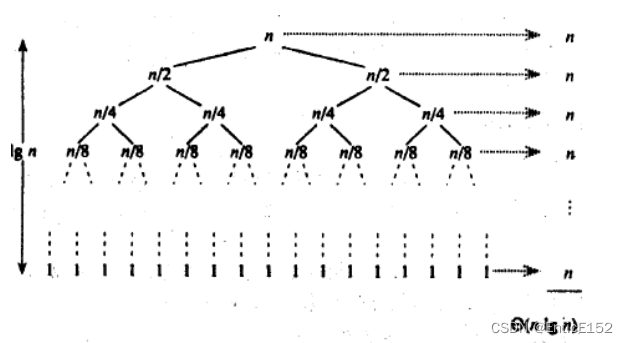
3.空间复杂度:O(logN)
4.稳定性:不稳定
8.归并排序
基本思想:
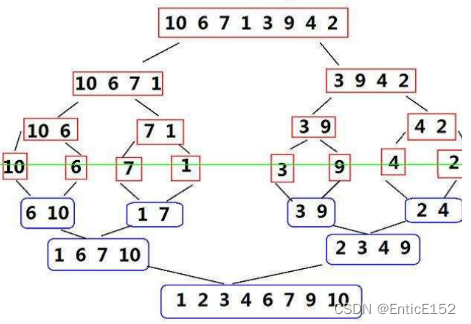
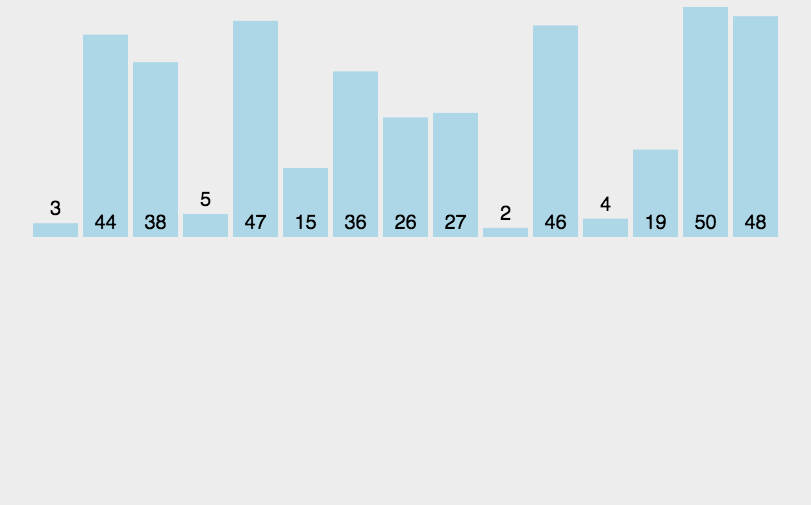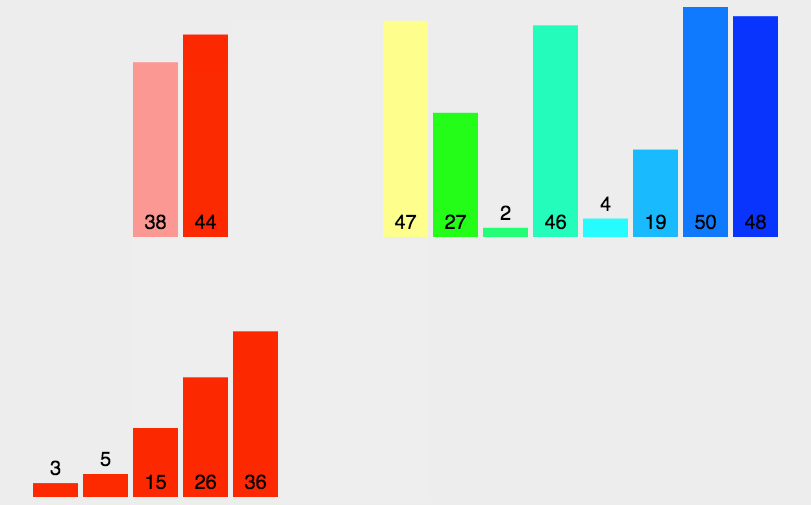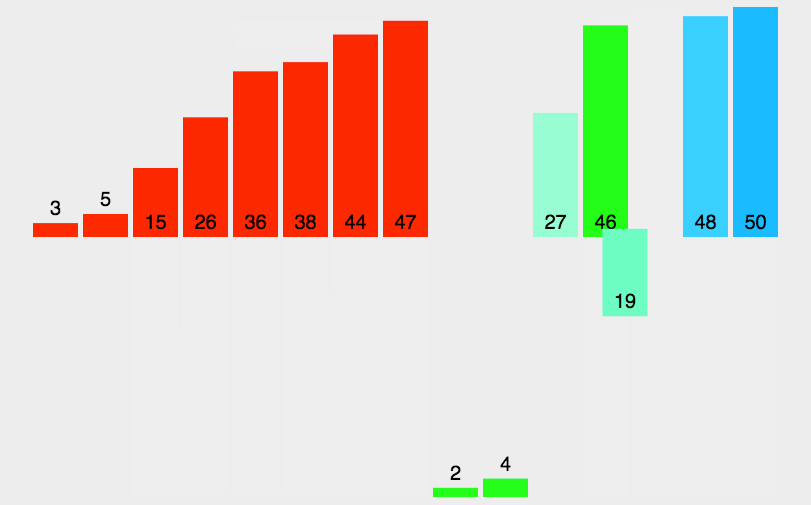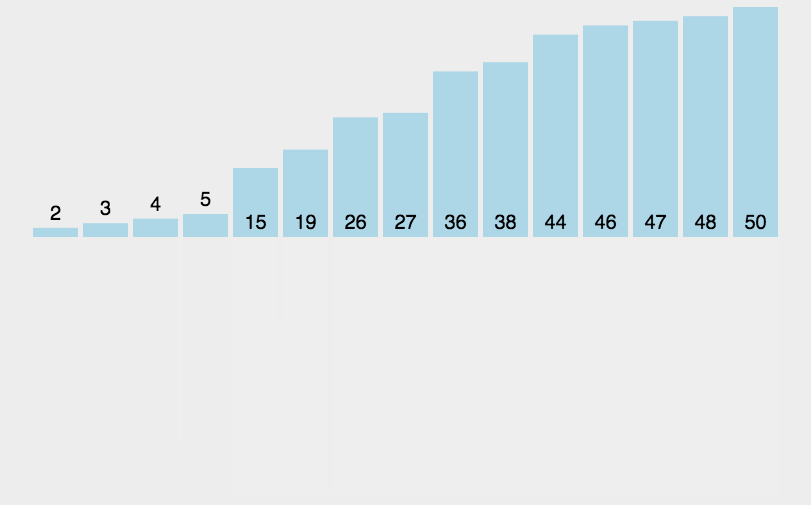
归并排序的特性总结:
//归并排序
//归并思想:左右区间均有序 取小的尾插到新数组
//归并排序的时间复杂度:O(N*logN) 空间复杂度为O(N)
//归并排序写子函数的原因:避免频繁malloc
void _MergeSort(int* a, int begin, int end, int* tmp)
{if (begin == end){return;}int mid = (end + begin) / 2;//[begin,mid] [mid+1,end]_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid + 1, end, tmp);//归并 取小的尾插//[begin,mid] [mid+1,end]int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}//拷贝回原数组——归并哪部分就拷贝哪部分回去memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}
void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}_MergeSort(a, 0, n - 1, tmp);free(tmp);tmp = NULL;
}归并排序非递归
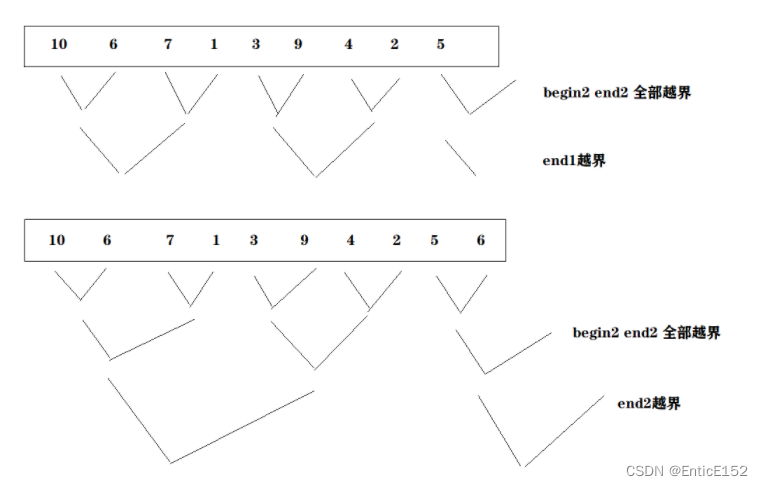
//归并排序的非递归
//问题:控制边界 该代码只能处理2的次方次个数据
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}int gap = 1;while (gap < n){//gap个数据 gap个数据进行归并for (int j = 0; j < n; j += 2 * gap){//归并 取小的尾插int begin1 = j, end1 = j + gap - 1;int begin2 = j + gap, end2 = j + 2 * gap - 1;int i = j;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}}//拷贝回原数组memcpy(a, tmp, n * sizeof(int));gap *= 2;} free(tmp);tmp = NULL;
}
//数据个数不一定是2的整数倍 计算直接按整数倍算的 存在越界 需要修正
//代码优化:控制边界
//三种越界情况:1.第一组end1越界 2.第二组全部越界 3.第三组部分越界
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}int gap = 1;while (gap < n){//gap个数据 gap个数据进行归并for (int j = 0; j < n; j += 2 * gap){//归并 取小的尾插int begin1 = j, end1 = j + gap - 1;int begin2 = j + gap, end2 = j + 2 * gap - 1;//第一组越界 第二组必然越界 只有一组不需要归并 直接跳出循环if (end1 >= n){break;}//第二组全部越界if (begin2 >= n)f{break;}//第二组部分越界if (end2 >= n){//修正一下end2 继续归并end2 = n - 1;}int i = j;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}//拷贝回原数组memcpy(a + j, tmp + j, (end2 - j + 1) * sizeof(int));}gap *= 2;printf("\n");}free(tmp);tmp = NULL;
}9.排序算法复杂度及稳定性分析
排序总结
直接插入排序最好的时间复杂度是O(N)最坏的时间复杂度是O(N^2)
希尔排序时间复杂度是O(N^1.3)
选择排序最好的时间复杂度是O(N^2)最坏的时间复杂度是O(N^2)
堆排序最好的时间复杂度是O(N*logN)最坏的时间复杂度是O(N*logN)
冒泡排序最好的时间复杂度是O(N)最坏的时间复杂度是O(N^2)
快速排序最好的时间复杂度是O(N*logN)最坏的时间复杂度是O(N^2)
归并排序最好的时间复杂度是O(N*logN)最坏的时间复杂度是O(N)
快速排序的空间复杂度是O(logN)归并排序的空间复杂度是O(N)
稳定性:数组中相同的值 排完序相对顺序可以做到不变就是稳定的 否则就不稳定
冒泡排序的稳定性好
选择排序的稳定性差
插入排序的稳定性好
希尔排序的稳定性差
堆排序的稳定性差
归并排序的稳定性好
快速排序的稳定性差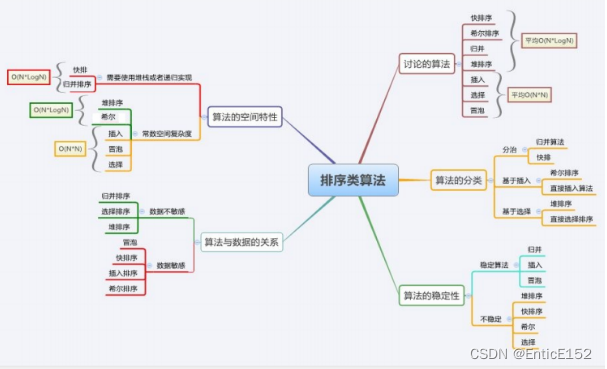
10.排序选择题练习
1. 快速排序算法是基于( )的一个排序算法。
A分治法
B贪心法
C递归法
D动态规划法
2.对记录(54,38,96,23,15,72,60,45,83)进行从小到大的直接插入排序时,当把第8个记录45插入到有序表时,为找到插入位置需比较( )次?(采用从后往前比较)
A 3
B 4
C 5
D 6
3.以下排序方式中占用O(n)辅助存储空间的是
A 简单排序
B 快速排序
C 堆排序
D 归并排序
4.下列排序算法中稳定且时间复杂度为O(n2)的是( )
A 快速排序
B 冒泡排序
C 直接选择排序
D 归并排序
5.关于排序,下面说法不正确的是
A 快排时间复杂度为O(N*logN),空间复杂度为O(logN)
B 归并排序是一种稳定的排序,堆排序和快排均不稳定
C 序列基本有序时,快排退化成冒泡排序,直接插入排序最快
D 归并排序空间复杂度为O(N), 堆排序空间复杂度的为O(logN)
6.下列排序法中,最坏情况下时间复杂度最小的是( )
A 堆排序
B 快速排序
C 希尔排序
D 冒泡排序
7.设一组初始记录关键字序列为(65,56,72,99,86,25,34,66),则以第一个关键字65为基准而得到的一趟快
速排序结果是()
A 34,56,25,65,86,99,72,66
B 25,34,56,65,99,86,72,66
C 34,56,25,65,66,99,86,72
D 34,56,25,65,99,86,72,66
答案:
1.A
2.C
3.D
4.B
5.D
6.A
7.A相关文章:

[数据结构]排序算法
目录 常用排序算法的实现:: 1.排序的概念及其运用 2.插入排序 3.希尔排序 4.选择排序 5.冒泡排序 6.堆排序 7.快速排序 8.归并排序 9.排序算法复杂度及稳定性分析 10.排序选择题练习 常用排序算法的实现:: 1.排序的概念及其运用…...
不愧是2023年就业最难的一年,还好有车企顶着~
就业龙卷风已经来临,以前都说找不到好的工作就去送外卖,但如今外卖骑手行业都已经接近饱和状态了,而且骑手们的学历也不低,本科学历都快达到了30%了,今年可以说是最难找到工作的一年。 像Android 开发行业原本就属于在…...
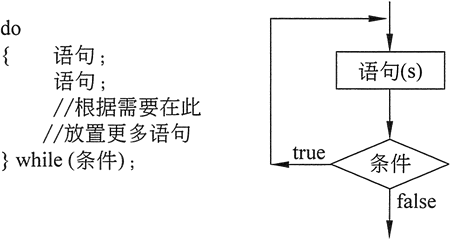
C/C++之while(do-while)详细讲解
目录 while循环有两个重要组成部分: while 是一个预测试循环 无限循环 do-while 循环 while循环有两个重要组成部分: 进行 true 值或 false 值判断的表达式;只要表达式为 true 就重复执行的语句或块;图 1 显示了 while 循环的…...
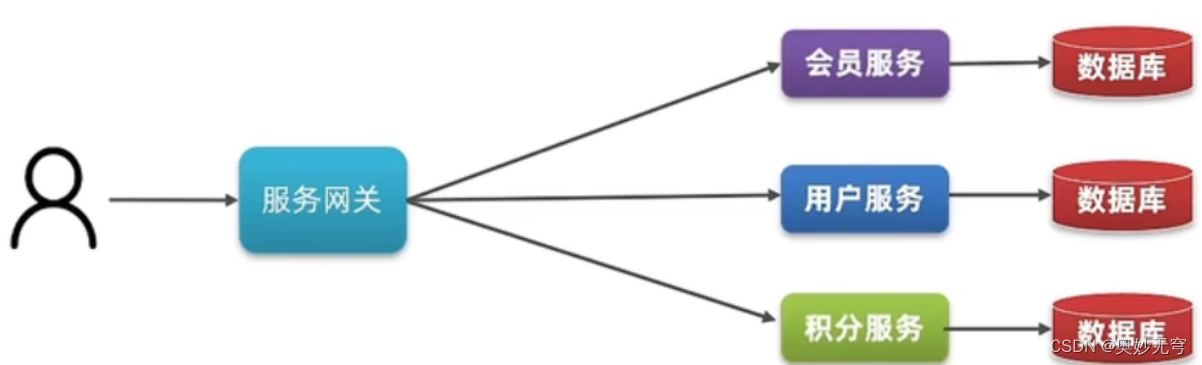
SpringCloud学习笔记(一)认识微服务
一、微服务技术栈 二、单体架构和分布式架构的区别 1、单体架构: 将业务的所有功能集中在一个项目中开发,打成一个包进行部署 优点:架构简单,部署成本低缺点:耦合度高 2、分布式架构: 根据业务功能对系统…...

Unity中使用WebSocket (ws://)的方法
WebSocket使得客户端和服务器之间的数据交换变得更加简单,允许服务端主动向客户端推送数据。在WebSocket API中,浏览器和服务器只需要完成一次握手,两者之间就直接可以创建持久性的连接,并进行双向数据传输。 WebSocket与http 其…...

米哈游春招算法岗-2023.03.19-第一题-交换字符-简单题
交换字符Problem Description 米小游拿到了一个仅由小写字母组成的字符串,她准备进行恰好一次操作:交换两个相邻字母,在操作结束后使得字符串的字典序尽可能大。 请你输出最终生成的字符串。 input 一个仅由小写字母组成的字符串,…...

能把爬虫讲的这么透彻的,没有20年功夫还真不行【0基础也能看懂】
前言 可以说很多人学编程,不玩点爬虫确实少了很多意思,不管是业余、接私活还是职业爬虫,爬虫世界确实挺精彩的。 今天来给大家浅谈一下爬虫,目的是让准备学爬虫或者刚开始起步的小伙伴们,对爬虫有一个更深更全的认知…...
springcloud学习总结
springcloud 构建微服务项目步骤 导入依赖编写配置文件开启这个功能 Enablexxx配置类 于2023年2月24日下午17点38分开始学习于2023年3月17日晚上20点26分学完总结代码地址:https://gitee.com/liang-weihao/StudySpringcloud学习笔记地址:https://www.…...
2022年亏损超10亿,告别野蛮成长的众安在线急需新“引擎”
2023年3月21日,众安在线披露了2022年财报,营收233.52亿元,同比增长6.44%;净亏损16.33亿元,去年同期净利润为11.6亿元,同比由盈转亏。 尽管众安在线再次身陷亏损的泥潭,但投资者却没有选择逃离。…...

ChatGPT文心一言逻辑大比拼(一)
❤️觉得内容不错的话,欢迎点赞收藏加关注😊😊😊,后续会继续输入更多优质内容❤️👉有问题欢迎大家加关注私戳或者评论(包括但不限于NLP算法相关,linux学习相关,读研读博…...
【机器学习面试总结】————特征工程
【机器学习面试总结】————特征工程一、特征归一化为什么需要对数值类型的特征做归一化?二、类别型特征在对数据进行预处理时,应该怎样处理类别型特征?三、高维组合特征的处理什么是组合特征?如何处理高维组合特征?四、组合特征怎样有效地找到组合特征?五、文本表示模型…...
如何将字符串反转?
参考答案 使用 StringBuilder 或 StringBuffer 的 reverse 方法,本质都调用了它们的父类 AbstractStringBuilder 的 reverse 方法实现。(JDK1.8)不考虑字符串中的字符是否是 Unicode 编码,自己实现。递归1. public AbstractStrin…...
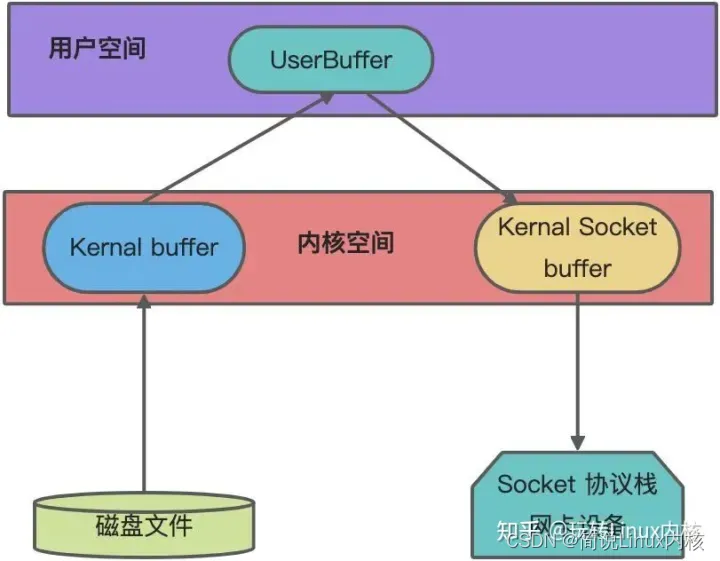
Linux内核IO基础知识与概念
什么是 IO在计算机操作系统中,所谓的I/O就是 输入(Input)和输出(Output),也可以理解为读(Read)和写(Write),针对不同的对象,I/O模式可以划分为磁盘…...
paper文献和科研小工具
一、好用的网站 Aminer 二、好用的工具 1. SciSpace SciSpace官网 【ChatGPT 论文阅读神器】SciSpace 用户注册与实战测试 SciSpace是一款基于 ChatGPT 的论文阅读神器。 2. ReadPaper 强大且超实用的论文阅读工具——ReadPaper ReadPaper官网 ReadPaper下载链接 Rea…...

dfs和bfs能解决的问题
一.理解暴力穷举之dfs和bfs暴力穷举暴力穷举是在解决问题中最常用的手段,而dfs和bfs算法则是这个手段的两个非常重要的工具。其实,最简单的穷举法是直接遍历,如数列求和,遍历一个数组即可求得所问答案,这与我在前两篇博…...

静态通讯录,适合初学者的手把手一条龙讲解
数据结构的顺序表和链表是一个比较困难的点,初见会让我们觉得有点困难,正巧C语言中有一个类似于顺序表和链表的小程序——通讯录。我们今天就来讲一讲通讯录的实现,也有利于之后顺序表和链表的学习。 目录 0.通讯录的初始化 1.菜单的创建…...
【你不知道的 CSS】你写的 CSS 太过冗余,以至于我对它下手了
:is() 你是否曾经写过下方这样冗余的CSS选择器: .active a, .active button, .active label {color: steelblue; }其实上面这段代码可以这样写: .active :is(a, button, label) {color: steelblue; }看~是不是简洁了很多! 是的,你可以使用…...

Lesson 8.1 决策树的核心思想与建模流程
文章目录一、借助逻辑回归构建决策树1. 决策树实例2. 决策树知识补充2.1 决策树简单构建2.2 决策树的分类过程2.3 决策树模型本质2.4 决策树的树生长过程2.5 树模型的基本结构二、决策树的分类与流派1. ID3(Iterative Dichotomiser 3) 、C4.5、C5.0 决策树2. CART 决策树3. CHA…...

【算法】FIFO先来先淘汰算法分析和编码实战
背景 在设计一个系统的时候,由于数据库的读取速度远小于内存的读取速度 为加快读取速度,将一部分数据放到内存中称为缓存,但内存容量是有限的,当要缓存的数据超出容量,就需要删除部分数据 这时候需要设计一种淘汰机制…...
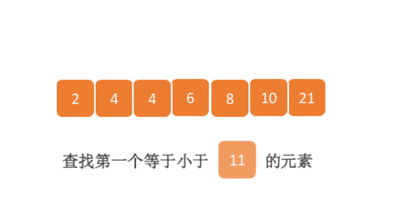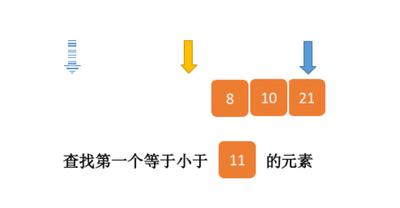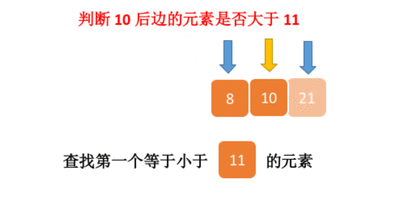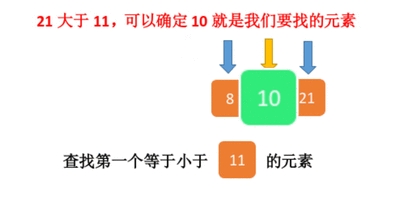
二分查找——我欲修仙(功法篇)
个人主页:【😊个人主页】 系列专栏:【❤️我欲修仙】 学习名言:临渊羡鱼,不如退而结网——《汉书董仲舒传》 系列文章目录 第一章 ❤️ 二分查找 文章目录系列文章目录前言🚗🚗🚗二分查找&…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...