力扣热题100_回溯_78_子集
文章目录
- 题目链接
- 解题思路
- 解题代码
题目链接
78. 子集
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
解题思路
回溯算法
下面我们根据回溯算法三步走,写出对应的回溯算法。
- 1.明确所有选择:根据数组中每个位置上的元素选与不选两种选择。
- 2.明确终止条件:当遍历到决策树的叶子节点时,就终止了。即当前路径搜索到末尾时,递归终止。
- 3.将决策树和终止条件翻译成代码:
- 定义回溯函数:
- backtracking(nums, index): 函数的传入参数是 nums(可选数组列表)和 index(代表当前正在考虑元素是 nums[i] ),全局变量是 res(存放所有符合条件结果的集合数组)和 path(存放当前符合条件的结果)。
- backtracking(nums, index): 函数代表的含义是:在选择 nums[index] 的情况下,递归选择剩下的元素。
- 书写回溯函数主体(给出选择元素、递归搜索、撤销选择部分)。
- 从当前正在考虑元素,到数组结束为止,枚举出所有可选的元素。对于每一个可选元素:
-
约束条件:之前选过的元素不再重复选用。每次从 index 位置开始遍历而不是从 0 位置开始遍历就是为了避免重复。集合跟全排列不一样,子集中 {1, 2} 和 {2, 1} 是等价的。为了避免重复,我们之前考虑过的元素,就不再重复考虑了。
-
选择元素:将其添加到当前子集数组 path 中。
-
递归搜索:在选择该元素的情况下,继续递归考虑下一个位置上的元素。
-
撤销选择:将该元素从当前子集数组 path 中移除。
for i in range(index, len(nums)): # 枚举可选元素列表path.append(nums[i]) # 选择元素backtracking(nums, i + 1) # 递归搜索path.pop() # 撤销选择
-
- 从当前正在考虑元素,到数组结束为止,枚举出所有可选的元素。对于每一个可选元素:
- 明确递归终止条件(给出递归终止条件,以及递归终止时的处理方法)。
- 当遍历到决策树的叶子节点时,就终止了。也就是当正在考虑的元素位置到达数组末尾(即 start >= len(nums))时,递归停止。
- 从决策树中也可以看出,子集需要存储的答案集合应该包含决策树上所有的节点,应该需要保存递归搜索的所有状态。所以无论是否达到终止条件,我们都应该将当前符合条件的结果放入到集合中。
- 定义回溯函数:
解题代码
class Solution:def subsets(self, nums: List[int]) -> List[List[int]]:res = [] # 存放所有符合条件结果的集合path = [] # 存放当前符合条件的结果def backtracking(nums, index): # 正在考虑可选元素列表中第 index 个元素res.append(path[:]) # 将当前符合条件的结果放入集合中if index >= len(nums): # 遇到终止条件(本题)returnfor i in range(index, len(nums)): # 枚举可选元素列表path.append(nums[i]) # 选择元素backtracking(nums, i + 1) # 递归搜索path.pop() # 撤销选择backtracking(nums, 0)return res
参考资料:datawhalechina
相关文章:

力扣热题100_回溯_78_子集
文章目录 题目链接解题思路解题代码 题目链接 78. 子集 给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。 解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。 示例 1: 输入ÿ…...
进程架构)
浏览器如何工作(一)进程架构
分享cosine 大佬,版权©️大佬所有 浏览器的核心功能 浏览器,“浏览” 是这个产品的核心,浏览无非分为两步: 获取想浏览的资源 展示得到的资源 现代浏览器还增加了交互功能,这涉及到脚本运行。因此,…...

【LeetCode】两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案,并且你不能使用两次相同的元素。 你可以按任意顺序返回答案。 示例 1…...
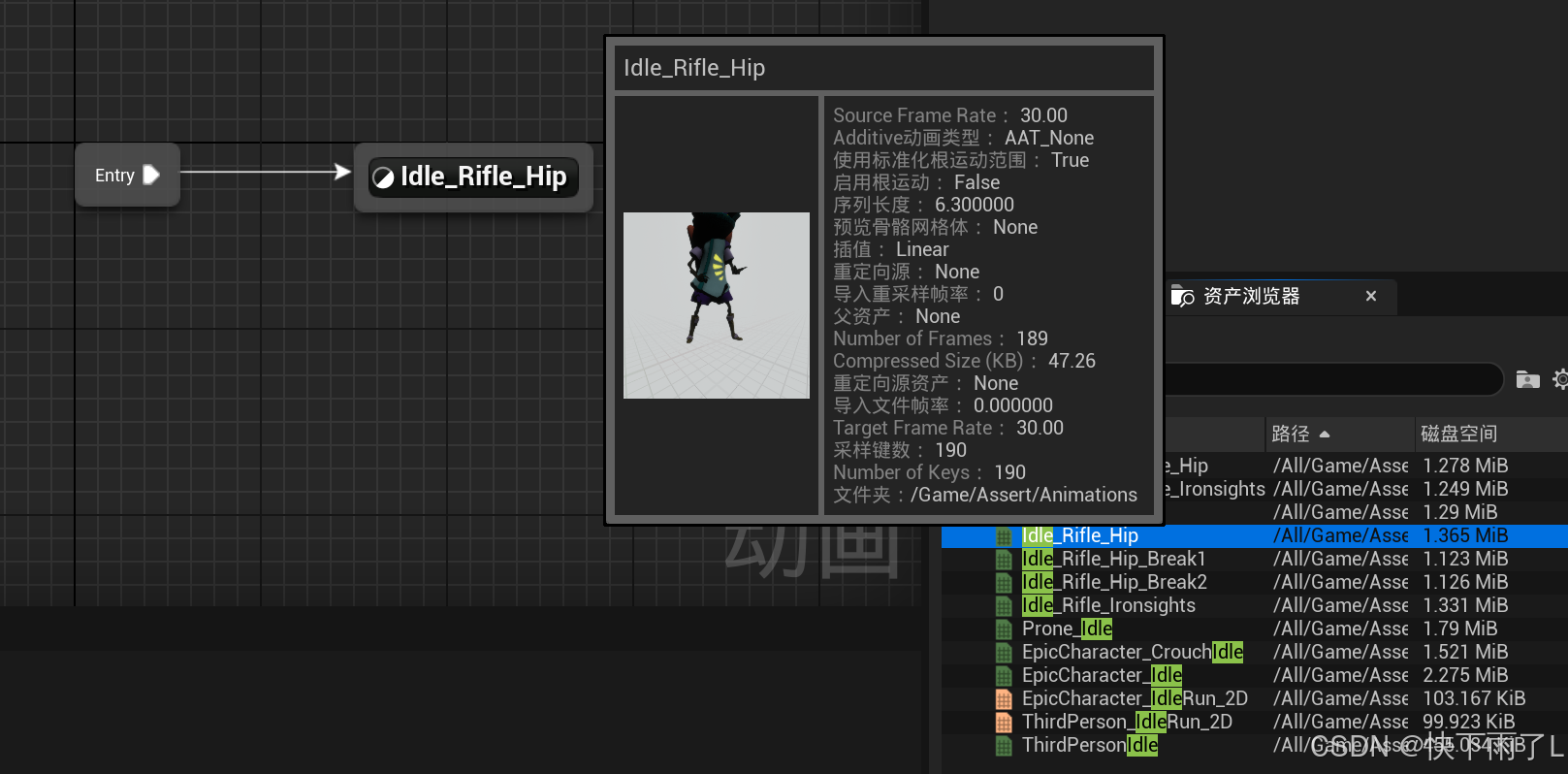
UE5学习笔记11-为拿取武器添加动画
一、一点说明 动画实例通过扩展为所有机器上的每个字符都存在动画蓝图,动画实例只能访问该计算机上的变量。 二、思路 我在武器组件中有一个武器类的指针,判断当前指针是否为空去判断当前角色是否装备武器 三、实现 1.在角色C类中添加是否装备武器的函…...
 】)
68. 文本左右对齐【 力扣(LeetCode) 】
一、题目描述 给定一个单词数组 words 和一个长度 maxWidth ,重新排版单词,使其成为每行恰好有 maxWidth 个字符,且左右两端对齐的文本。 你应该使用 “贪心算法” 来放置给定的单词;也就是说,尽可能多地往每行中放置单…...
【中等】 猿人学web第一届 第6题 js混淆-回溯
文章目录 请求流程请求参数 加密参数定位r() 方法z() 方法 加密参数还原JJENCOde js代码加密环境检测_n("jsencrypt")12345 计算全部中奖的总金额请求代码注意 请求流程 请求参数 打开 调试工具,查看数据接口 https://match.yuanrenxue.cn/api/match/6 请…...

低、中、高频率段具体在不同应用中的范围是多少
1、低频率段(Low Frequency Range) ①建筑声学和噪声控制:通常将20 Hz 到 200 Hz 的频率范围视为低频段。在这一范围内,声音的波长较长,通常与低音(如重低音音乐)和建筑结构中的振动有关。 ②…...

Oxford Model600 Model400低温氦压缩机cryogenic helium compressor手侧
Oxford Model600 Model400低温氦压缩机cryogenic helium compressor手侧...

Golang面试题四(并发编程)
目录 1.Go常见的并发模型 2.哪些方法安全读写共享变量 3.如何排查数据竞争问题 4.Go有哪些同步原语 1. Mutex (互斥锁) 2. RWMutex (读写互斥锁) 3. Atomic 3.1.使用场景 3.2.整型操作 3.3.指针操作 3.4.使用示例 4. Channel 使用场景 使用示例 5. sync.WaitGr…...
计算机学生高效记录并整理编程学习笔记的方法
哪些知识点需要做笔记? 以下是我认为计算机学生大学四年可以积累的笔记。 ① 编程语言类(C语言CJava):保留课堂笔记中可运行的代码部分,课后debug跑一跑。学习语言初期应该多写代码(从仿写到自己写&#…...

【书生大模型实战】L2-LMDeploy 量化部署实践闯关任务
一、关卡任务 基础任务(完成此任务即完成闯关) 使用结合W4A16量化与kv cache量化的internlm2_5-7b-chat模型封装本地API并与大模型进行一次对话,作业截图需包括显存占用情况与大模型回复,参考4.1 API开发(优秀学员必做)使用Func…...

《编程学习笔记之道:构建知识宝库的秘诀》
在编程的浩瀚世界里,我们如同勇敢的探险家,不断追寻着知识的宝藏。而高效的笔记记录和整理方法,就像是我们手中的指南针,指引着我们在这片知识海洋中前行,不至于迷失方向。在这篇文章中,我们将深入探讨如何…...

DETR论文,基于transformer的目标检测网络 DETR:End-to-End Object Detection with Transformers
transformer的基本结构: encoder-decoder的基本流程为: 1)对于输入,首先进行embedding操作,即将输入映射为向量的形式,包含两部分操作,第一部分是input embedding:例如,在NLP领域&…...

untiy有渲染线程和逻辑线程嘛
之前我也这么认为,其实unity引擎是单线程的,当然后续的jobs不在考虑范围内 如果你在一个awake 或者 start方法中 延时,是会卡住主线程的 比如 其实游戏引擎有一个基础简单理解,那就是不断的进行一个循环,在这个周期循…...
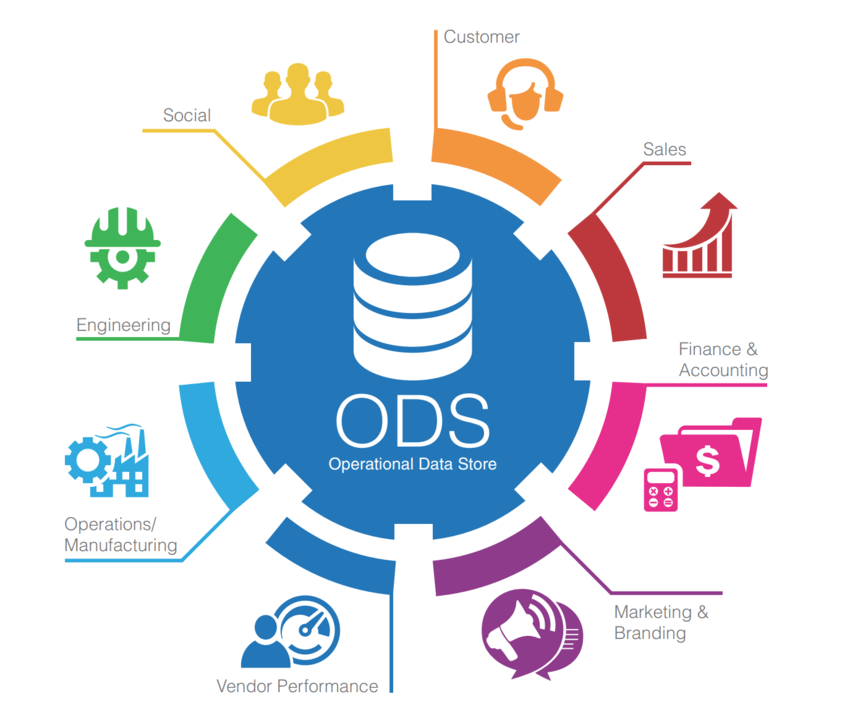
什么是数据仓库ODS层?为什么需要ODS层?
在大数据时代,数据仓库的重要性不言而喻。它不仅是企业数据存储与管理的核心,更是数据分析与决策支持的重要基础。而在数据仓库的各个层次中,ODS层(Operational Data Store,操作型数据存储)作为关键一环&am…...

permutation sequence(
60. Permutation Sequence class Solution:def getPermutation(self, n: int, k: int) -> str:def rec(k, l, ans, n):if(n0): return# 保留第一个位置,剩下数字的组合leftCom math.factorial(n - 1) #用于计算 (n-1) 的阶乘值ele k // leftCommod k % leftCo…...

PCL 三线性插值
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 三线性插值是一种在三维空间中使用已知数据点进行插值的方法。它是在立方体内的插值方法,通过利用立方体的八个顶点的已知值来估算立方体内任意一点的值。三线性插值扩展了一维的线性插值和二维的双线性插值。其基…...

JVM虚拟机(一)介绍、JVM内存模型、JAVA内存模型,堆区、虚拟机栈、本地方法栈、方法区、常量池
目录 学习JVM有什么用、为什么要学JVM? JVM是什么呢? 优点一:一次编写,到处运行。(Write Once, Run Anywhere,WORA) 优点二:自动内存管理,垃圾回收机制。 优点三&am…...

Python利用xlrd复制一个Excel中的sheet保留原格式创建一个副本(注:xlrd只能读取xls)
目录 专栏导读库的介绍库的安装完整代码总结 专栏导读 🌸 欢迎来到Python办公自动化专栏—Python处理办公问题,解放您的双手 🏳️🌈 博客主页:请点击——> 一晌小贪欢的博客主页求关注 👍 该系列文…...

40、Python之面向对象:扩展的对象属性解析顺序(描述符 + MRO)
引言 在上一篇文章中,我们简单回顾了Python中在继承语境下的属性解析顺序,同时补充了能够控制、影响属性解析的3个函数/方法(2个魔术方法 1个内置函数),相信对Python中属性的解析,相较于MRO,有…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
