二叉树遍历
二叉树的遍历是二叉树操作中的一个基本且重要的概念,它指的是按照一定的规则访问二叉树中的每个节点,并且每个节点仅被访问一次。常见的二叉树遍历方式有四种:前序遍历(Pre-order Traversal)、中序遍历(In-order Traversal)、后序遍历(Post-order Traversal)和层序遍历(Level-order Traversal)。
1. 前序遍历(Pre-order Traversal)
前序遍历的顺序是:根节点 -> 左子树 -> 右子树。对于每个节点,都遵循这个顺序进行遍历。
- 递归实现:
void preorderTraversal(TreeNode root) { if (root == null) return; System.out.print(root.val + " "); // 访问根节点 preorderTraversal(root.left); // 遍历左子树 preorderTraversal(root.right); // 遍历右子树 } - 非递归(迭代)实现(使用栈):
void preorderTraversalIterative(TreeNode root) { Stack<TreeNode> stack = new Stack<>(); if (root != null) stack.push(root); while (!stack.isEmpty()) { TreeNode node = stack.pop(); System.out.print(node.val + " "); // 访问节点 if (node.right != null) stack.push(node.right); // 先右后左保证左子树先遍历 if (node.left != null) stack.push(node.left); } }2. 中序遍历(In-order Traversal)
中序遍历的顺序是:左子树 -> 根节点 -> 右子树。这常用于二叉搜索树(BST)中,因为这样可以得到一个有序的节点序列。
- 递归实现
void inorderTraversal(TreeNode root) { if (root == null) return; inorderTraversal(root.left); // 遍历左子树 System.out.print(root.val + " "); // 访问根节点 inorderTraversal(root.right); // 遍历右子树 } - 非递归(迭代)实现(使用栈):
void inorderTraversalIterative(TreeNode root) { Stack<TreeNode> stack = new Stack<>(); TreeNode curr = root; while (curr != null || !stack.isEmpty()) { while (curr != null) { stack.push(curr); curr = curr.left; // 遍历到最左节点 } curr = stack.pop(); // 弹出栈顶元素 System.out.print(curr.val + " "); // 访问节点 curr = curr.right; // 转向右子树 } }3. 后序遍历(Post-order Traversal)
后序遍历的顺序是:左子树 -> 右子树 -> 根节点。
- 递归实现:
void postorderTraversal(TreeNode root) { if (root == null) return; postorderTraversal(root.left); // 遍历左子树 postorderTraversal(root.right); // 遍历右子树 System.out.print(root.val + " "); // 访问根节点 } - 非递归(迭代)实现(使用栈):
void postorderTraversalIterative(TreeNode root) { Stack<TreeNode> stack = new Stack<>(); TreeNode prev = null; // 用于记录上一次访问的节点 while (root != null || !stack.isEmpty()) { while (root != null) { stack.push(root); root = root.left; // 遍历到最左节点 } root = stack.peek(); // 弹出栈顶元素但不移除 // 如果右子树为空或者右子树已经访问过,则访问当前节点 if (root.right == null || root.right == prev) { stack.pop(); System.out.print(root.val + " "); // 访问节点 prev = root; root = null; // 回到上层循环,检查是否有其他节点需要访问 } else { root = root.right; // 否则,转向右子树 } } }4. 层序遍历
-
非递归(迭代)实现(使用队列)
import java.util.LinkedList; import java.util.Queue; class TreeNode { int val; TreeNode left; TreeNode right; TreeNode(int x) { val = x; } } public class BinaryTreeLevelOrderTraversal { public void levelOrderTraversal(TreeNode root) { if (root == null) return; Queue<TreeNode> queue = new LinkedList<>(); queue.offer(root); // 将根节点加入队列 while (!queue.isEmpty()) { TreeNode currentNode = queue.poll(); // 从队列中取出一个节点 System.out.print(currentNode.val + " "); // 访问该节点 // 如果左子节点不为空,则将其加入队列 if (currentNode.left != null) { queue.offer(currentNode.left); } // 如果右子节点不为空,则将其加入队列 if (currentNode.right != null) { queue.offer(currentNode.right); } } } } -
非递归(迭代)实现
-
实际上,层序遍历不常使用递归实现,因为递归本质上是栈的操作,而层序遍历需要的是队列。但我们可以借助一些额外的数据结构(如数组或链表)来模拟层序遍历的效果,但这通常不是推荐的做法,因为它违背了层序遍历的本意。
相关文章:

二叉树遍历
二叉树的遍历是二叉树操作中的一个基本且重要的概念,它指的是按照一定的规则访问二叉树中的每个节点,并且每个节点仅被访问一次。常见的二叉树遍历方式有四种:前序遍历(Pre-order Traversal)、中序遍历(In-…...

uni app 调用前置摄像头
uniapp开发app并没有相关Api调用前置摄像头。只能使用5app的api 调用前置摄像头拍照 plus.camera.getCamera(index) 获取需要操作的摄像头对象,如果要进行拍照或摄像操作,需先通过此方法获取摄像头对象 index指定要获取摄像头的索引值,1表…...

哈工大李治军老师OS课程笔记(4)——内存管理
一 内存使用与分段(实验六) 内存是如何用起来的? 内存使用:将程序放在内存中,PC指向开始地址 重定位:修改程序中的地址(是相对地址) 什么时候完成重定位? 编译时加基址…...

代码随想录算法训练营第43天:动态规划part10:子序列问题
300.最长递增子序列 力扣题目链接(opens new window) 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2…...

传智教育引通义灵码进课堂,为技术人才教育学习提效
7 月 17 日,阿里云与传智教育在阿里巴巴云谷园区签署合作协议,双方将基于阿里云智能编程助手通义灵码在课程共建、品牌合作及产教融合等多个领域展开合作,共同推进 AI 教育及相关业务的发展,致力于培养适应未来社会需求的高素质技…...
企业信息化建设搞得好了叫系统工程,搞不好叫面子工程
2024-06-13 09:26贝格前端工场...

程序员如何平衡日常编码工作与提升式学习?
在快速变化的编程领域中,平衡日常编码工作与个人成长确实是一个重要且富有挑战性的议题。以下是我对这一问题的看法和建议: 1. 认识到平衡的重要性 首先,理解两者之间的平衡并非零和游戏,而是相辅相成的。高效的编码工作能够为个…...

Linux---文件系统和日志分析
文章目录 文件系统和日志分析inode和block概述inode包含文件的元信息用stat命令可以查看某个文件的inode信息Linux系统文件三个主要的时间属性 目录文件的结构用户通过文件名打开文件时,系统内部的过程查看inode号码的方法硬盘分区后的结构访问文件的简单流程inode的…...

MySQL 体系架构
文章目录 一. MySQL 分支与变种1. Drizzle2. MariaDB3. Percona Server 二. MySQL的替代1. Postgre SQL2. SQLite 三. MySQL 体系架构1.连接层2 Server层(SQL处理层)3. 存储引擎层1)MySQL官方存储引擎概要2)第三方引擎3࿰…...

跨站脚本攻击漏洞
1.JavaScript JavaScript 是一种脚本,一门编程语言,它可以在网页上实现复杂的功能,网页展现给你的不再是简单的静态信息,而是实时的内容更新,交互式的地图,2D/3D动画,滚动播放的视频等等。 &a…...
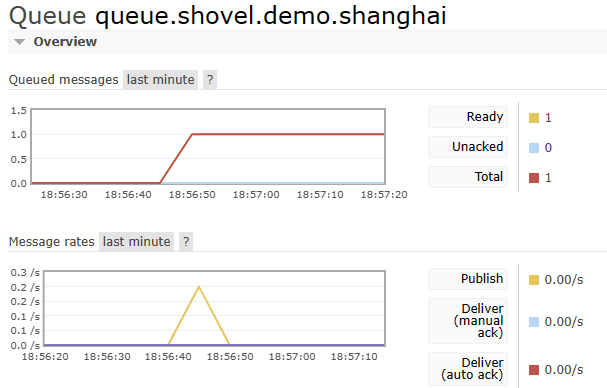
RabbitMQ入门与进阶
RabbitMQ入门与进阶 基础篇1. 为什么需要消息队列?2. 什么是消息队列?3. RabbitMQ体系结构介绍4. RabbitMQ安装5. HelloWorld6. RabbitMQ经典用法(工作模式)7. Work Queues8. Publish/Subscribe9. Routing10. Topics 进阶篇1. RabbitMQ整合SpringBoot2. 消息可靠性投递故障情…...

Unity新输入系统 之 InputActions(输入配置文件)
本文仅作笔记学习和分享,不用做任何商业用途 本文包括但不限于unity官方手册,unity唐老狮等教程知识,如有不足还请斧正 首先你应该了解新输入系统的基本单位Unity新输入系统 之 InputAction(输入配置文件最基本的单位࿰…...

Linux运维篇-误删/bin,/sbin目录怎么修复系统
这里写自定义目录标题 前言实例挂载镜像,重启系统进入救援模式拷贝镜像系统中的/bin和/sbin目录到原系统重启系统 总结 前言 当你看到这篇文章的时候,你的系统可能已经无法登录,或者正在处于登录状态但是不能执行任何常规的命令,…...

构建高效外贸电商系统的技术探索与源码开发
在当今全球化的经济浪潮中,外贸电商作为连接国内外市场的桥梁,其重要性日益凸显。一个高效、稳定、功能全面的外贸电商系统,不仅能够助力企业突破地域限制,拓宽销售渠道,还能提升客户体验,增强品牌竞争力。…...

Java设计模式:中介者模式详解与最佳实践
Java设计模式:中介者模式详解与最佳实践 1. 引言 在软件开发过程中,特别是复杂系统的构建中,模块间的交互往往成为影响代码质量的重要因素。当模块之间耦合度过高时,系统的维护、扩展和理解成本都会显著增加。为了降低模块之间的…...

Matlab绘制像素风字母颜色及透明度随机变化动画
本文是使用 Matlab 绘制像素风字母颜色及透明度随机变化动画的教程 实现效果 实现代码 如果需要更改为其他字母组合,在下面代码的基础上简单修改就可以使用。 步骤:(1) 定义字母形状;(2) 给出字母组合顺序;(3) 重新运行程序&#…...

C:每日一题:二分查找
1、知识介绍: 1.1 概念: 二分查找是一种在有序数组中查找某一特定元素的搜索算法 1.2 基本思想: 每次将待查找的范围缩小一半,通过比较中间元素与目标元素的大小,来决定是在左半部分还是右半部分继续查找。 举个生…...

python Django中使用ORM进行分组统计并降序排列
python Django中使用ORM进行分组统计并降序排列 # 使用supplier和Count进行分组统计,其中supplier为MyModel的一个字段 supplier_counts MyModel.objects.values(supplier).annotate(countCount(supplier)).order_by(-count) # 输出统计结果 for supplier_count in supplier_…...

QT C++ 编写modbus 总结
[开源库的使用]libModbus编译及使用_libmodbus库-CSDN博客 libmodbus的下载与编译_modbus库文件下载-CSDN博客 【QT5】解决 QT 界面中文显示乱码问题_qt5输出中文乱码解决方法-CSDN博客 Qt:解决qt修改完ui文件起不到作用_qt ui文件修改后不生效-CSDN博客...

基于SpringBoot的网络海鲜市场系统的设计与实现
TOC springboot219基于SpringBoot的网络海鲜市场系统的设计与实现 绪论 1.1 选题背景 当人们发现随着生产规模的不断扩大,人为计算方面才是一个巨大的短板,所以发明了各种计算设备,从结绳记事,到算筹,以及算盘&…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
