蓝桥杯每日一真题—— [蓝桥杯 2021 省 AB2] 完全平方数(数论,质因数分解)
文章目录
- [蓝桥杯 2021 省 AB2] 完全平方数
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 样例 #2
- 样例输入 #2
- 样例输出 #2
- 提示
- 思路:
- 理论补充:完全平方数的一个性质:完全平方数的质因子的指数一定为偶数
- 最终思路:
- 小插曲:
- 全部代码
[蓝桥杯 2021 省 AB2] 完全平方数
题目描述
一个整数 aaa 是一个完全平方数,是指它是某一个整数的平方,即存在一个 整数 bbb,使得 a=b2a=b^{2}a=b2 。
给定一个正整数 nnn,请找到最小的正整数 xxx,使得它们的乘积是一个完全平方数。
输入格式
输入一行包含一个正整数 nnn。
输出格式
输出找到的最小的正整数 xxx。
样例 #1
样例输入 #1
12
样例输出 #1
3
样例 #2
样例输入 #2
15
样例输出 #2
15
提示
对于 30%30 \%30% 的评测用例, 1≤n≤10001 \leq n \leq 10001≤n≤1000,答案不超过 100010001000。
对于 60%60 \%60% 的评测用例,1≤n≤1081 \leq n \leq 10^{8}1≤n≤108,答案不超过 10810^{8}108。
对于所有评测用例,1≤n≤10121 \leq n \leq 10^{12}1≤n≤1012,答案不超过 101210^{12}1012。
蓝桥杯 2021 第二轮省赛 A 组 G 题(B 组 H 题)。
思路:
这一看直接暴力就只能得一点点分,我还数论学的不太好先暴力得了30分。然后开始想办法吧!
没办法。。。看答案吧。。。
理论补充:完全平方数的一个性质:完全平方数的质因子的指数一定为偶数
1.唯一分解定理任意一个数 n,它都可以分解为若干个质数的乘积。
2.需要知道完全平方数的一个性质:完全平方数的质因子的指数一定为偶数。附上大佬的证明过
程:

最终思路:
对n进行质因数分解,如果质因数的指数为奇数的话就在x中乘以这个质因子这样,可以让指数保持偶数,如果是偶数那就不用管它~~~~
1.分解质因子:
for (long long i = 2; i * i <= n; i++){if (n % i == 0){cnt++;//记录有多少个因子,后面好遍历}while (n % i == 0){a[cnt] = i;//a数组存因子g[cnt]++;//g数组存因子指数n = n / i;}}if (n > 1){a[++cnt] = n;g[cnt]++;}//考虑没分解完的情况
2,根据性质得出答案:
for (int i = 1; i <= cnt; i++)//遍历如果有奇数就让原来的n*ans*这个奇数质因子也就是让ans*这个奇数质因子{if (g[i] % 2){ans = ans * a[i];}}cout << ans;
小插曲:
质因数分解写错了最后输出了和n一样的数竟然得了60分!!
全部代码
#include <iostream>
using namespace std;long long n, ans = 1, g[1000], a[1000], cnt;
int main()
{cin >> n;// 首先对n进行质因数分解for (long long i = 2; i * i <= n; i++){if (n % i == 0){cnt++;//记录有多少个因子,后面好遍历}while (n % i == 0){a[cnt] = i;//a数组存因子g[cnt]++;//g数组存因子指数n = n / i;}}if (n > 1){a[++cnt] = n;g[cnt]++;}//考虑没分解完的情况//完全平方数的质因子的指数一定为偶数for (int i = 1; i <= cnt; i++)//遍历如果有奇数就让原来的n*ans*这个奇数质因子也就是让ans*这个奇数质因子{if (g[i] % 2){ans = ans * a[i];}}cout << ans;system("pause");return 0;
}相关文章:

蓝桥杯每日一真题—— [蓝桥杯 2021 省 AB2] 完全平方数(数论,质因数分解)
文章目录[蓝桥杯 2021 省 AB2] 完全平方数题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1样例 #2样例输入 #2样例输出 #2提示思路:理论补充:完全平方数的一个性质:完全平方数的质因子的指数一定为偶数最终思路:小插曲&am…...
Linux编辑器-vim
一、vim简述1)vi/vim2)检查vim是否安装2)如何用vim打开文件3)vim的几种模式命令模式插入模式末行模式可视化模式二、vim的基本操作1)进入vim(命令行模式)2)[命令行模式]切换至[插入模式]3)[插入模式]切换至[命令行模式]4)[命令行模…...
5G将在五方面彻底改变制造业
想象一下这样一个未来,智能机器人通过在工厂车间重新配置自己,从多条生产线上组装产品。安全无人机处理着从监视入侵者到确认员工停车等繁琐的任务。自动驾驶汽车不仅可以在建筑物之间运输零部件,还可以在全国各地运输。工厂检查可以在千里之…...

http和https的区别?
http和https的区别?HTTPHTTPSHTTP与HTTPS区别HTTPS相比于HTTP协议的优点和缺点HTTP http是超文本传输协议 HTTP协议是基于传输层的TCP协议进行通信,通用无状态的协议。80端口 HTTPS https—安全的超文本传输协议 是以安全为目标的HTTP通道,…...
【Spring Cloud Alibaba】4.创建服务消费者
文章目录简介开始搭建创建项目修改POM文件添加启动类添加配置项添加Controller添加配置文件启动项目测试访问Nacos访问接口查看端点检查简介 接下来我们创建一个服务消费者,本操作先要完成之前的步骤,详情请参照【Spring Cloud Alibaba】Spring Cloud A…...
C语言——动态内存管理 malloc、calloc、realloc、free的使用
目录 一、为什么存在动态内存分配 二、动态内存函数的介绍 2.1malloc和free 2.2calloc 2.3realloc 三、常见的动态内存错误 3.1对NULL指针的解引用操作 3.2对动态开辟空间的越界访问 3.3对非动态开辟的内存使用free释放 3.4使用free释放一块动态开辟内存的一部分 3.5…...

技术分享——Java8新特性
技术分享——Java8新特性1.背景2. 新特性主要内容3. Lambda表达式4. 四大内置核心函数式接口4.1 Consumer<T>消费型接口4.2 Supplier<T>供给型接口4.3 Function<T,R>函数型接口4.4 Predicate<T> 断定型接口5. Stream流操作5.1 什么是流以及流的类型5.2…...

vue基础知识大全
1,指令作用 以v-开头,由vue提供的attribute,为渲染DOM应用提供特殊的响应式行为,也即是在表达式的值发生变化的时候响应式的更新DOM。其内容为可以被求值的js代码,可以写在return后面被返回的表达式。 指令的简写指令简…...
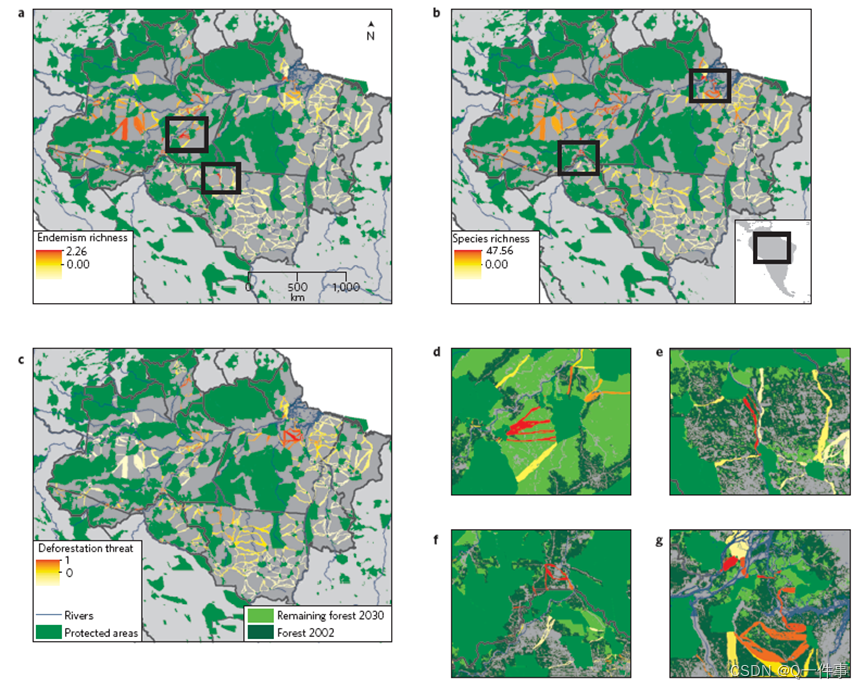
第2篇|文献研读|nature climate change|减缓气候变化和促进热带生物多样性的碳储量走廊
研究背景 从 2000 年到 2012 年,潮湿和干燥热带地区的森林总损失超过 90,000 平方公里 yr-1,这主要是由农业扩张驱动的。热带森林砍伐向大气中排放 0:95 Pg C yr-1 并导致广泛的生物多样性丧失。保护区的生物多样性取决于与保护区所在的更广泛景观的生态…...

从暴力递归到动态规划(2)小乖,你也在为转移方程而烦恼吗?
前引:继上篇我们讲到暴力递归的过程,这一篇blog我们将继续对从暴力递归到动态规划的实现过程,与上篇类似,我们依然采用题目的方式对其转化过程进行论述。上篇博客:https://blog.csdn.net/m0_65431718/article/details/…...

Leetcode.1638 统计只差一个字符的子串数目
题目链接 Leetcode.1638 统计只差一个字符的子串数目 Rating : 1745 题目描述 给你两个字符串 s和 t,请你找出 s中的非空子串的数目,这些子串满足替换 一个不同字符 以后,是 t串的子串。换言之,请你找到 s和 t串中 恰…...
KoTime:v2.3.9新增线程管理(线程统计、状态查询等)
功能概览 KoTime的开源版本已经迭代到了V2.3.9,目前功能如下: 实时监听方法,统计运行时长web展示方法调用链路,瓶颈可视化追踪追踪系统异常,精确定位到方法接口超时邮件通知,无需实时查看线上热更新&…...

直面风口,未来不仅是中文版ChatGPT,还有AGI大时代在等着我们
说到标题的AI2.0这个概念的研究早在2015年就研究起步了,其实大家早已知道,人工智能技术必然是未来科技发展战略中的重要一环,今天我们就从AI2.0入手,以GPT-4及文心一言的发布为切入角度,来谈一谈即将降临的AGI时代。 关…...
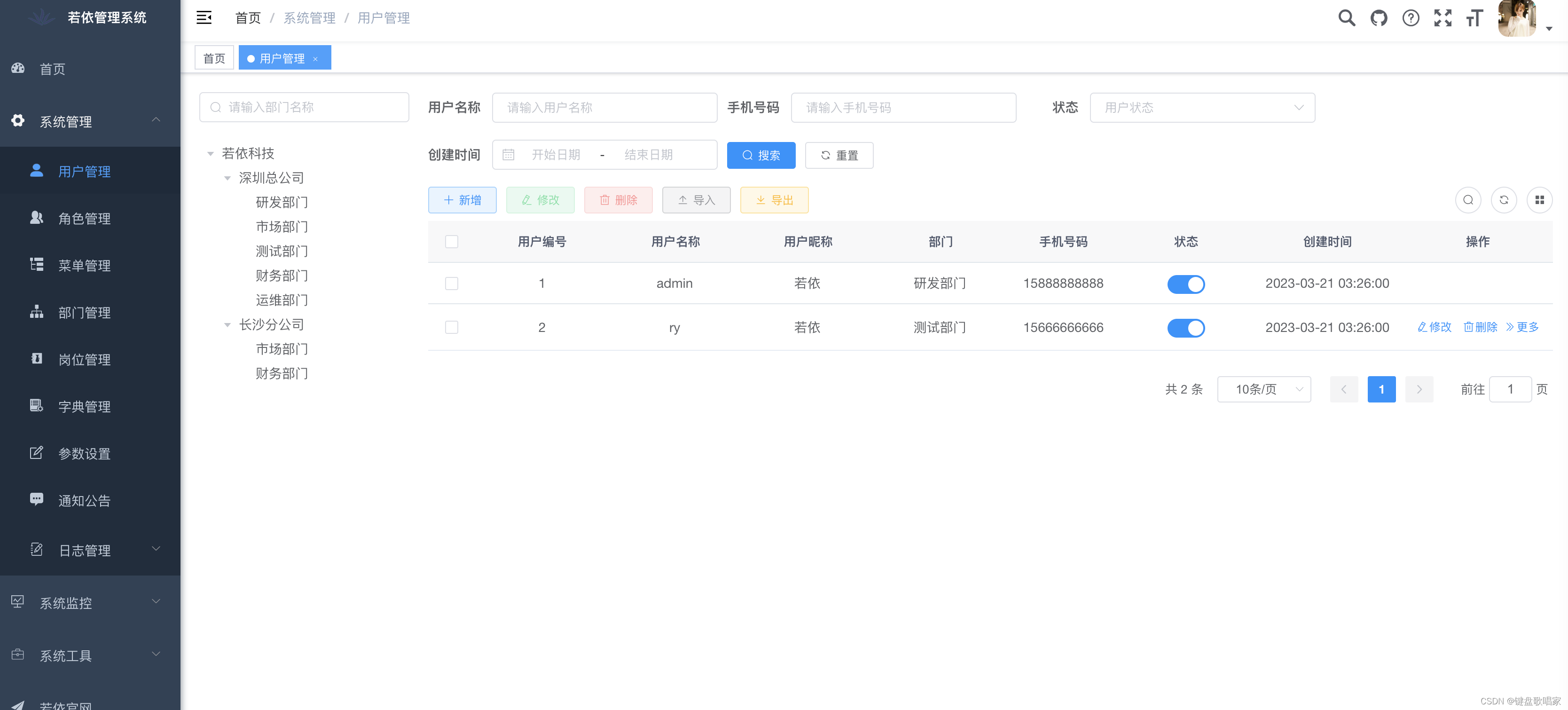
若依微服务(ruoyi-cloud)保姆版容器编排运行
一、简介 项目gitee地址:https://gitee.com/y_project/RuoYi-Cloud 由于该项目运行有很多坑,大家可以在git克隆拷贝到本地后,执行下面的命令使master版本回退到本篇博客的版本: git reset --hard 05ca78e82fb4e074760156359d09a…...
vue2图片预览插件
学习:vue插件开发实例-图片预览插件 vue2-pre-img-plugin的gitee代码 准备工作 准备图片与基础的样式 将iconfont下载的字体图标资源放在src/assets/iconfont目录下将准备预览的图片放到src/static/images目录下 PrevImg.vue 在plugins/PrevImg目录下ÿ…...

手写Promise源码的实现思路
Promise的使用: let promise new Promise((resolve, reject) > {resolve("OK");// reject("Error"); });console.log(promise);promise.then(value > {console.log("success"); }, error > {console.log("fail"…...

【数据结构】-关于树的概念和性质你了解多少??
作者:小树苗渴望变成参天大树 作者宣言:认真写好每一篇博客 作者gitee:gitee 如 果 你 喜 欢 作 者 的 文 章 ,就 给 作 者 点 点 关 注 吧! 树前言一、树概念及结构1.1树的概念1.2 树的相关概念1.3 树的表示1.4树在实际中的运用…...

【前端之旅】NPM必知必会
一名软件工程专业学生的前端之旅,记录自己对三件套(HTML、CSS、JavaScript)、Jquery、Ajax、Axios、Bootstrap、Node.js、Vue、小程序开发(UniApp)以及各种UI组件库、前端框架的学习。 【前端之旅】Web基础与开发工具 【前端之旅】手把手教你安装VS Code并附上超实用插件…...

Android SQLite使用事务来确保所有语句都以原子方式执行及保证数据完整性一次执行多条语句示例
execSQL 不支持用分号分隔一次执行多个 SQL 语句,虽然理论上可以实现。但是,并不建议这样做,因为这可能会导致潜在的 SQL 注入漏洞。相反,建议使用 execSQL 或 rawQuery 分别执行每个语句。 在下面的代码块中,我们正在…...
nodejs+vue校园超市小卖部零食在线购物商城系统
21世纪的今天,随着社会的不断发展与进步,人们对于信息科学化的认识,已由低层次向高层次发展,由原来的感性认识向理性认识提高,管理工作的重要性已逐渐被人们所认识,科学化的管理,使信息存储达到…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...
