自动化与高效设计:推理技术在FPGA中的应用
想象一下,你正在设计一个复杂的电路系统,就像在搭建一座精巧的积木城堡。你手头有各种形状和功能的积木块,这些积木块可以组合成任何你需要的结构。在这个过程中,你有两种主要的方法:一种是手动挑选和搭建每一块积木,另一种是告诉一个聪明的助手你想要的结果,让他根据你的描述自动帮你搭建。
这两种方法在硬件设计中就对应着“实例化”(Instantiation)和“推理”(Inference)。而推理(Inference)在FPGA设计中的应用为硬件设计带来了极大的便利和效率提升。

FPGA,即现场可编程门阵列。它的特别之处在于,你可以通过编写代码来重新配置它,实现各种不同的功能。如信号处理、数据计算,而实现这些功能的关键,就是一种叫做硬件描述语言(HDL)的工具。
在用HDL编写代码时,我们有两种主要的方法来实现硬件设计:实例化和推理。
通过实例化,你可以明确地告诉FPGA需要哪些硬件组件,比如查找表(LUT)、触发器(FF)等。这样的好处是,你可以完全控制每一个细节,确保设计的每一部分都符合你的要求。
而推理则是另一种方法。它更加自动化,你只需要编写高级的描述代码,FPGA会根据这些描述自动生成相应的硬件实现。这种方法的好处是可以简化设计流程,让你更专注于设计的整体功能,而不必纠结于每一个细节。
然而,推理也有其局限性。在某些情况下,推理生成的硬件实现可能不如你亲自实例化的那么高效。因此,在设计过程中需要仔细权衡和选择,确保最终的实现既高效又可靠。
总之,FPGA设计中的推理和实例化方法各有优劣。了解和掌握这两种方法的使用,可以帮助你更好地实现高效的硬件设计。

如果你对FPGA设计感兴趣,想要深入了解推理和实例化的奥秘,我们推出了Xilinx官方的《Inference》课程,欢迎你来听。

通过这个课程,你将学会如何利用推理功能来简化设计流程,提高设计效率,并最终打造出属于你的完美“积木城堡”。
——
学习入口(PC端打开):
zzfpga.com/StudentPlatform/Course/CourseLibrary![]() http://zzfpga.com/StudentPlatform/Course/CourseLibrary
http://zzfpga.com/StudentPlatform/Course/CourseLibrary
相关文章:
自动化与高效设计:推理技术在FPGA中的应用
想象一下,你正在设计一个复杂的电路系统,就像在搭建一座精巧的积木城堡。你手头有各种形状和功能的积木块,这些积木块可以组合成任何你需要的结构。在这个过程中,你有两种主要的方法:一种是手动挑选和搭建每一块积木&a…...

对react模块和模块化理解
在React开发中,模块化和React模块是两个紧密相关但又有区别的概念。理解它们对于构建高效、可维护的React应用至关重要。 模块化 模块化是一种将大型代码库拆分成更小、更易于管理的部分(即模块)的软件设计技术。每个模块都封装了特定的功能…...

CAN总线-----帧格式
目录 前言 一、CAN总线帧格式分类 1.数据帧(重点) 2.遥控帧 3.错误帧 4.过载帧 5.间隔帧 二、位填充 三、波形实例 前言 本期我们就开始学习CAN总线的帧格式,对应帧格式的话,在前面我们学习I2C协议和SPI协议等协议的时候…...

UE网络同步(一) —— 一个项目入门UE网络同步之概念解释
最近在学习UE网络同步,发现了一个非常好的教程,并且附带了项目文件,这里从这个小项目入手,理解UE的网络同步 教程链接:https://www.youtube.com/watch?vJOJP0CvpB8w 项目链接:https://github.com/awforsyt…...

MATLAB中rsf2csf函数用法
目录 语法 说明 示例 将实数 Schur 形式变换为复数 Schur 形式 rsf2csf函数的功能是将实数 Schur 形式转换为复数 Schur 形式。 语法 [Unew,Tnew] rsf2csf(U,T) 说明 [Unew,Tnew] rsf2csf(U,T) 将实矩阵 X 的 [U,T] schur(X) 的输出从实数 Schur 形式变换为复数 Sc…...

Java基础 文字小游戏
souf System.out.printf("你好啊%s","张三") 输出你好啊张三 System.out.printn()放在中间可以换行 System.out.printf("%s你好啊%s","张三","李四") 输出 张三你好啊李四 只有输出没有换行效果。 制作一个文字小游戏…...
)
「数组」归并排序 / if语句优化|小区间插入优化(C++)
概述 在上一篇文章中,我们介绍了快速排序以及随机快速排序: 「数组」快速排序 / 随机值优化|小区间插入优化(C) 今天,我们来介绍归并排序。 相比于快速排序是冒泡排序融合了分治思想后形成的究极promax进化版&…...
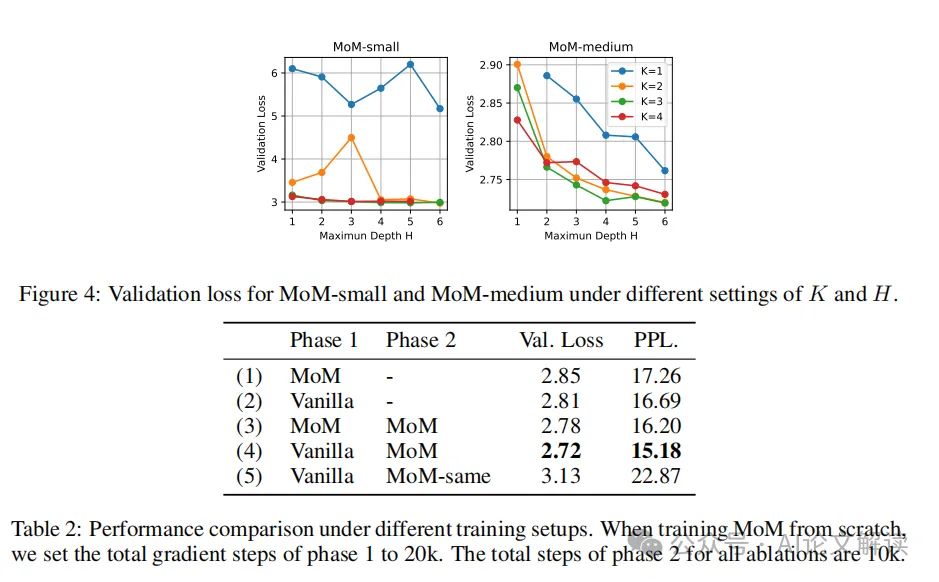
颠覆传统 北大新型MoM架构挑战Transformer模型,显著提升计算效率
挑战传统的Transformer模型设计 在深度学习和自然语言处理领域,Transformer模型已经成为一种标准的架构,广泛应用于各种任务中。传统的Transformer模型依赖于一个固定的、按深度排序的层次结构,每一层的输出都作为下一层的输入。这种设计虽然…...

接口优化笔记
索引 添加索引 where条件的关键自动或者order by后面的排序字段可以添加索引加速查询 索引只能通过删除新增进行修改,无法直接修改。 # 查看表的索引 show index from table_name; show create table table_name; # 添加索引 alter table table_name add index …...

pandas 科学计数法显示
我注意到pandas中有一个问题, 默认情况下,就是其中的数据的小数位不能超过6位,比如0.0000007就会被显示为0,这个结果如下 全部以科学技术显示 import pandas as pd import numpy as np# 设置显示格式为科学计数法 pd.options.d…...

PHP正则替换字符串中的图片地址
在PHP中,可以使用preg_replace()函数来实现正则表达式的替换功能。以下是一个简单的例子,演示如何替换字符串中的图片地址。 double $str 图片地址1:<img src"http://example.com/image1.jpg"> 图片地址2:<i…...

基于多商户AI智能名片商城小程序的粉丝忠诚度提升策略:深度融合足额法则与多维度激励体系
摘要:在数字化浪潮的推动下,多商户AI智能名片商城小程序以其独特的商业模式和技术优势,正逐步成为连接商家与消费者,特别是粉丝群体的重要平台。本文深入探讨了如何通过深度融合足额法则与多维度激励体系,有效提升多商…...

BigDecimal高精度运算
1. BigDecimal是什么类型,为什么可以转为double BigDecimal 是 Java 中用于表示任意精度的十进制数的类。它主要用于金融和商业计算,能够提供比 double 类型更高精度的运算,特别是在处理货币等需要精确计算的场景中。 1.1 BigDecimal 的基…...

C/C++实现蓝屏2.0
🚀欢迎互三👉:程序猿方梓燚 💎💎 🚀关注博主,后期持续更新系列文章 🚀如果有错误感谢请大家批评指出,及时修改 🚀感谢大家点赞👍收藏⭐评论✍ 前…...

Unity音频管理器插件AudioToolKit
Unity音频管理器插件AudioToolKit 介绍AudioToolKit介绍具体用法总结 介绍 最近在自己写音频管理器的时候在网上发现了一款比较好用并且功能很全的一个音频管理插件,叫做AudioToolKit的插件。 如果需要的可以直接从我资源中找AudioToolKit。 AudioToolKit介绍 A…...
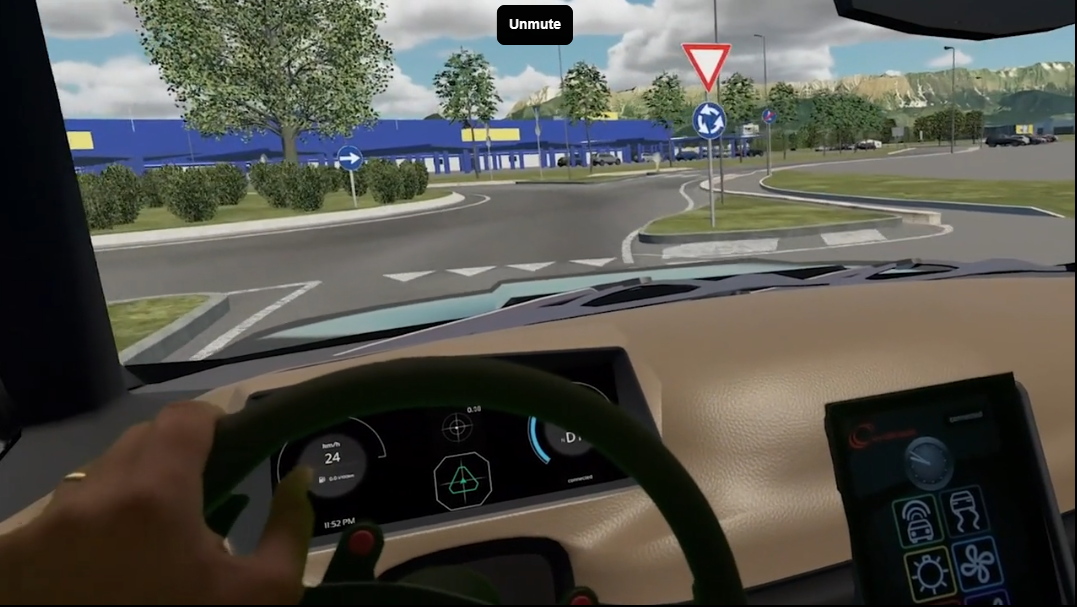
搜维尔科技:驾驶模拟器背后的技术: Varjo的虚拟/混合现实 (VR/XR)提供独特的优势,最终加快汽车开发创新的步伐
专业驾驶模拟器广泛应用于车辆开发,帮助汽车行业在开发过程的早期做出更好的设计决策。总体目标是为测试驾驶员提供最真实的驾驶体验,包括动态动作和声音,并测试控制算法或辅助系统等功能。环境越真实,驾驶员的体验就越接近最终车…...

OSL 冠名赞助Web3峰会 “FORESIGHT2024”圆满收官
OSL 望为香港数字资产市场发展建设添砖加瓦 (香港,2024 年 8 月 13 日)- 8 月 11 日至 12 日, 由 香港唯一专注数字资产的上市公司 OSL 集团(863.HK)冠名赞助,Foresight News、 Foresight Ventu…...

LeetCode 3148.矩阵中的最大得分:每个元素与其左或上元素之差的最大值(原地修改O(1)空间)
【LetMeFly】3148.矩阵中的最大得分:每个元素与其左或上元素之差的最大值(原地修改O(1)空间) 力扣题目链接:https://leetcode.cn/problems/maximum-difference-score-in-a-grid/ 给你一个由 正整数 组成、大小为 m x n 的矩阵 g…...

主流的开源大型语言模型
本期我们来聊聊目前主流的开源大型语言模型。这些模型就像是AI界的超级英雄,各具特色,为我们的研究和开发提供了强大的力量。🚀 GPT-Neo:这是EleutherAI的杰作,它模仿了OpenAI的GPT-3。GPT-Neo虽然规模小一些…...

【自动驾驶】话题通信
目录 构建发布者构建订阅者编写lanch文件自动启动节点测试运行ROS的目录结构 切换到工作空间的src目录下: 构建发布者 catkin_create_pkg publisher std_msgs rospy roscpp编写发布者程序: // 1.包含头文件 #include "ros/ros.h" #include &…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...
