“蓝桥杯”递推和递归(一)——取数位
1. 算法简介
递推和递归虽然叫法不同,但它们的基本思想是一致的,在很多程序中,这两种算法可以通用,不同的是递推法效率更高,递归法更方便阅读。
(1)递推法
递推法是一种重要的数学方法,同时也是计算机进行数值计算的个重要算法。
递推法的核心是找到计算前后过程之间的数量关系,即递推式。递推式往往根据已知条件和所求问题之间存在的某种相互联系推导得出。递推计算时,需要将复杂运算转换为若干步重复的简单运算,这样可以发挥计算机擅于重复处理数据的特点。递推法避开了求通项公式的麻烦,把一个复杂问题的求解分解成了连续的若干歩简单运算,可以将递推法看成一种特殊的迭代算法。
[案例解析]铺方格
有2×n个长方形的方格,用一个1×2的骨牌铺满方格。例如当0=3时为2×3方格,骨牌的铺放方案有3种,

骨牌铺设方案(1)
编写一个程序,试对给出的任意一个n(n>0)输出铺法总数。针对这个问题,要想直接获得问题的解答是相当困难的。可以用递推法,从简单到复杂逐步归纳出问题解的一般规律。分析过程如下。
当n=1时,只能有一种铺法 ,如图4-2(a)所示,铺法总数为X1=1。
当n=2时,骨牌可以并列竖排,也可以并列横排,再无其他排列方法,如图2(b)所示,铺法总数为X2 =2。
当n=3时,骨牌可以全部竖排,也可以认为在方格中已经有一个竖排骨牌、需要在方格中排列两个横排骨牌(无重复方法),若已经在方格中排列两个横排骨牌,则必须在方格中排列一个竖排骨牌,如图2(c)所示,再无其他排列方法,铺法总数为X3= 3。

骨牌铺放方案(2)
由此可以看出,当n=3时,排列骨牌的方法数是n=1和n=2时排列方法数之和。
推出一般规律,对一般的n,要求Xn。可以这样考虑:若第一个骨牌是竖排列,则剩下n-1个骨牌需要排列,这时排列方法数为Xn-1,若第一个骨牌是横排列,则整个方格至少有2个骨牌是横排列(1×2骨牌),因此剩下n-2个骨牌需要排列,这时排列方法数为Xn-2从第一种骨牌排列方法考虑,只有这两种可能,所以有:
Xn=Xn-1+Xn-2(n> 2)
X1=1
X2=2
Xn=Xn-1+ Xn-2就是问题求解的递推公式
任意n都可以从中获得解答。
例如n=5,
X3=X2+X1=3
X4=X3+X2=5
X5=X4+X3=8
利用程序表示为:
cin>>n;
a[1]=1;a[2]=2;
for(i=3;i<=n; i++)
a[i]=a[i-1]+a[i-2];
cout<<a[n]<<"";(2)递归法
在计算机科学中,如果某个函数的实现中出现了对函数自身的调用语句,则称该函数为递归函数。
递推法可以用递归函数实现。一般来说,循环递推法比递归函数的速度更快,但递归函数的可读性更强。
例如,上述平铺方格问题改写成递归函数的形式如下。
int pu(int n)
{
if(n==1) return 1;
if(n==2) return 2;
return pu(n-1) +pu(n-2);
}递归函数在它的函数体内直接或者间接地调用自身,每调用一次,就进入新的一层。递归函数必须有结束递归的条件。函数会一直递推 ,直到遇到结束 条件返回,递归函数调用的一般过程如图3所示,这里以n=6为例。
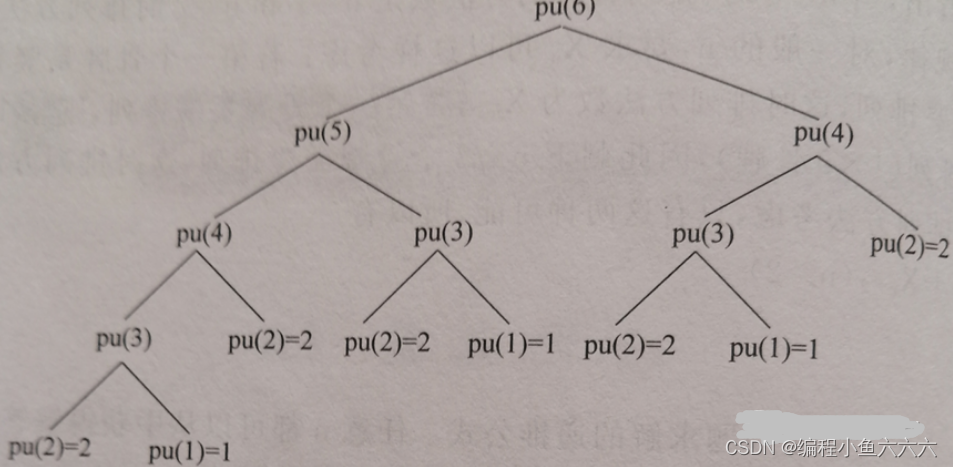
递归函数的调用过程
2. 取数位(2017年试题E)
【问题描述】
求一个整数的第k位数字有很多种方法,以下下方法就是其中一种。
//求x用十进制表示时的数位长度
int len(int x){
if(x<10) return 1;
return len(x/10)+1;
}
//取x的第k位数字
int f(int x, int k) {
if(len(x)-k==0) returnx%10;
return ( ) ;//填空
}
int main()
int x= 23574;
printf("&d\n", f(x,3));
return 0;
}对于题目中的测试数据,应该打印5。
请仔细分析源码,并补充画线部分缺少的代码。
注意:只提交缺失的代码,不要填写任何已有内容或说明性文字。
答案——取数位
//求 x 用十进制表示时的数位长度int len(int x){if(x<10) return 1;return len(x/10)+1;}//取 x 的第 k 位数字int f(int x, int k) {if(len(x)-k==0) return x%10;return f(x/10,k) ;//填空}int main()int x= 23574;printf("&d\n", f(x,3));return 0;}相关文章:

“蓝桥杯”递推和递归(一)——取数位
1. 算法简介 递推和递归虽然叫法不同,但它们的基本思想是一致的,在很多程序中,这两种算法可以通用,不同的是递推法效率更高,递归法更方便阅读。 (1)递推法 递推法是一种重要的数学方法&#…...

蓝桥杯·3月份刷题集训Day02
本篇博客旨在记录自已打卡蓝桥杯3月份刷题集训,同时会有自己的思路及代码解答希望可以给小伙伴一些帮助。本人也是算法小白,水平有限,如果文章中有什么错误之处,希望小伙伴们可以在评论区指出来,共勉💪。 文…...

python --获取内网IP地址
方法一 import socketdef get_local_ip_address():ip_address try:# 获取本机主机名hostname socket.gethostname()# 获取本机IPip_address socket.gethostbyname(hostname)except:passreturn ip_address方法二 import subprocessdef get_local_ip_address():ip_address …...

如何衡量你的Facebook广告活动的成功
投入大量资金和资源在Facebook广告上并不总能带来预期的回报,这很可能是由于缺乏恰当的衡量广告活动成功的方法。在这篇文章中,我们将介绍一些关键的指标,帮助你更好地了解如何衡量你的Facebook广告活动的成功。1.费用每次点击(CP…...

Linux对一个目录及其子目录所有文件添加权限
1、chmod指令 chmod是一个改变用户拥有指定文件的权限的命令.r:只读,w:写,x执行.也可以用数字 -rw------- (600) -- 只有属主有读写权限。 -rw-r--r-- (644) -- 只有属主有读写权限;而属组用户和其他用户只有读权限。 -rwx------ (700) -- 只有属主有读、写、执…...

宝刀未老?低代码何德何能受大厂们的推崇
风口之下,低代码蓬勃发展,本文从国内低代码的走红现象引入,浅析低代码发展中的变化趋势,重点探讨如此趋势之下,国内大厂如何通过低代码实现了良性发展。 一、国内爆火的低代码 据Gartner最新报告显示,到2…...
智能扑克牌识别软件(Python+YOLOv5深度学习模型+清新界面)
摘要:智能扑克牌识别软件利用视觉方法检测和识别日常扑克牌具体花色与数字,快速识别牌型并标注结果,帮助计算机完成扑克牌对战的前期识别步骤。本文详细介绍基于深度学习的智能扑克牌识别软件,在介绍算法原理的同时,给…...

SQL优化13连问,收藏好!
1.日常工作中,你是怎么优化SQL的? 大家可以从这几个维度回答这个问题: 分析慢查询日志 使用explain查看执行计划 索引优化 深分页优化 避免全表扫描 避免返回不必要的数据(如select具体字段而不是select*) 使用…...

【小技巧】公式从docx文件复制到doc文件变成了图片怎么办?
文章目录0、word文件后缀命名1、docx和doc默认的公式编辑方式2、MathTpye公式编辑器3、MathType 运行时错误‘53’:文件未找到:MathPage.WLL4、结束语0、word文件后缀命名 1997-2003的旧版本文件名后缀是.doc 从2007版以后,后缀名是.docx…...
Python3入门与进阶笔记(六):初识类
目录 一些解释 属性 类名建议首字母大写,通常用驼峰规则命名。变量名建议小写,下划线隔开。类最基本的作用是封装。 写在类内非方法中的语句在类加载的时候会执行,且只会执行一次,例如下面的print语句,类加载时就会…...

Prometheus监控实战系列九:主机监控
Prometheus使用各种Exporter来监控资源。Exporter可以看成是监控的agent端,它负责收集对应资源的指标,并提供接口给到Prometheus读取。不同资源的监控对应不同的Exporter,如node-exporeter、mysql-exporter、kafka-exporter等,在这…...

JVM知识整理
JVM知识整理 JVM的主要组成部分 JVM包含两个两个子系统(类加载子系统和执行引擎)和两个组件(运行时数据区与和本地库接口) 类加载子系统:根据给定的全限定类名来加载class文件到运行时数据区域中的方法区。执行引擎&a…...

【C++】二叉搜索树
A:你长大后想要做什么? B:写下“快乐”…… A:不,你理解错我的意思了,我是说 B:不,是你理解错了人生…… 文章目录一、二叉搜索树的实现1.struct TreeNode{}2.迭代版本2.1 Insert()插入结点(解决链接的问题)…...
leetcode -- 21. 合并两个有序链表
🐨目录📑1. 题目🛶2. 解法- 头插到新链表🐬2.1 思路🐬2.1 代码实现⛵3. 解法优化 - 带哨兵位🐋3.1 思路🐋3.2 代码实现🚤4. 题目链接📑1. 题目 将两个升序链表合并为一个…...

计算机组成原理|第四章(笔记)
目录第四章 存储器4.1 概述4.1.1 存储器分类4.1.2 存储器的层次结构4.2 主存储器4.2.1 概述4.2.2 半导体存储芯片简介4.2.3 随机存取存储器(RAM)4.2.4 只读存储器(ROM)4.2.5 存储器与CPU的连接4.2.6 存储器的校验4.2.7 提高访存速…...

【Unity3D-BUG记录】Unity3D中出现“动画片段必须标记为Legacy的警告”消除方法
推荐阅读 CSDN主页GitHub开源地址Unity3D插件分享简书地址我的个人博客 大家好,我是佛系工程师☆恬静的小魔龙☆,不定时更新Unity开发技巧,觉得有用记得一键三连哦。 一、前言 在开发中可能会遇到下面的警告: The AnimationClip…...
)
Spring Bean的定义(含创建Bean的三种方式)
🏆 文章目标:复习和理解下Spring Bean的定义 🍀 Spring Bean的定义(含创建Bean的三种方式) ✅ 创作者:Jay… 🎉 个人主页:Jay的个人主页 🍁 展望:若本篇讲解内…...
vue的路由-vue router(一)
vue的路由-vue router一、路由的基本使用HTMLrouter-linkrouter-viewJavaScript二、带参数的动态路由匹配三、嵌套路由四. 编程式导航导航到不同的位置替换当前位置横跨历史篡改历史五. 命名路由六. 命名视图嵌套命名视图七. 重定向和别名重定向别名八. 将 props 传递给路由组件…...
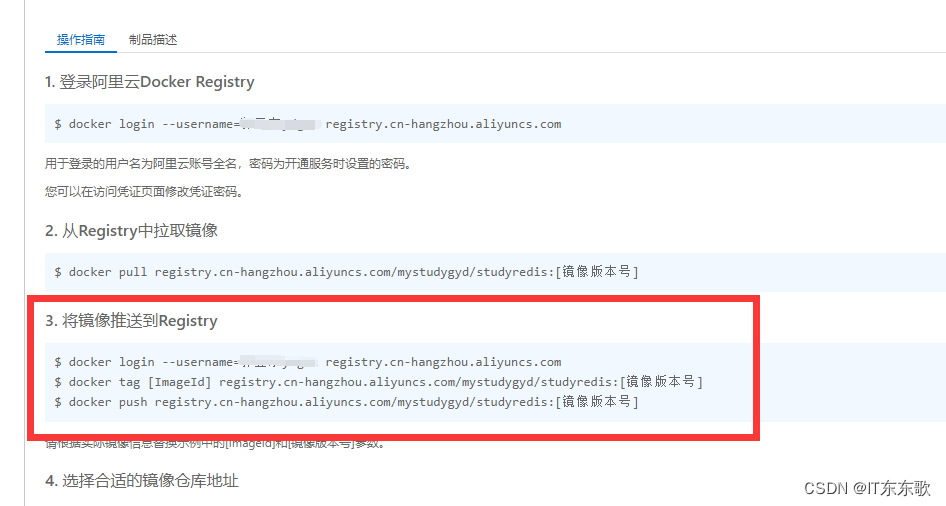
DevOps流水线搭建-PHP版本
一、介绍流水线发布代码1、官网https://www.jenkins.io/zh2、kubesphere里的介绍https://kubesphere.io/zh/docs/v3.3/devops-user-guide/how-to-use/pipelines/choose-jenkins-agent/3、git仓库可以自己写点测试代码,提交,待会测试用https://gitee.com/…...
)
C语言之按位取反~(七十一)
计算机存储数据基本知识计算机中二进制数包括(正数和负数)是以补码形式存储。符号位:补码的最左侧首位是符号位,0表示正数,1表示负数。二进制有三种形式:原码、反码、补码。正数的补码和反码:是…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...
