C语言之按位取反~(七十一)
计算机存储数据基本知识
计算机中二进制数包括(正数和负数)是以补码形式存储。
符号位:补码的最左侧首位是符号位,0表示正数,1表示负数。
二进制有三种形式:原码、反码、补码。
正数的补码和反码:是正数本身(原码)。
负数的反码:符号位不变(是1),其余位按位取反,不用加一。
负数的补码:符号位不变(是1),先按位取反,再加一。(即是反码加一)
在计算机内存中,负数以补码形式存在(即取反,再加一)。
计算机并不直接存储二进制原码,而是存储二进制的补码。正数的补码就是原码。比如1,原码0000 0001,补码也为0000 0001。就存储的是原码0000 00001.
而计算机不直接存储负数,而是存储负数的补码,负数的补码计算规则是"符号位不变,原码取反再加一"。
例如:-1怎么存储的?
原码1000 0001
取反1111 1110,
加一1111 1111
1111 1111就是-1的二进制补码。
当负数要输出给别的程序用的时候怎么办呢?总不能把存储的补码给别人的吧?给人用之前需要将补码逆向再转换成原码,否则数据就不对了。
负数转换补码的规则:取反,再加一,符号不变。
那么:
补码转换原码的规则:符号不变,先减一,再取反。
这样就得到原码,可以输出了。
将正数和负数按位取反(~)
特别注意:
"~"符号取反的用法,场景也不一样,同样是"~"符号,有的是求反码,有的是求补码,所以要搞清楚。
举两个例子说明:
<1>.代码示例一
#include <stdio.h>int main(){int a = 0;printf("~0 = %d\n",~a);a = 1;printf("~1 = %d\n",~a);a = 2;printf("~2 = %d\n",~a);a = -1;printf("~(-1) = %d\n",~a);a = -2;printf("~(-2) = %d\n",~a);
}打印:
~0 = -1
~1 = -2
~2 = -3
~(-1) = 0
~(-2) = 1~0步骤
步骤1:首先计算出0的补码,即它本身
步骤2:因为0的补码是负数,所以要还原其原码在输出;
0的补码和反码是他本身,再对0按位取反,就变成1111 1111,因为最高位为1,所以为负数,负数是以补码的形式存储,所以输出时要转换成正确的原码。
因为原码转补码的规则是:先取反,再加一
所以补码转原码的规则是:先减一,再取反。
步骤1:首先计算出0的补码,即它本身
0的原码的补码是他本身:
0000 0000步骤2:因为0的补码是负数,所以要还原其原码在输出
~0:即所有位数,按位取反
1111 1111当你要输出的时候,编译器发现最高位符号位是1,这个数是个负数,而负数在计算机里面是用补码存储的,所以此时计算机认为这个1111 1111是补码,它要转换成原码输出,于是先减去1,除了符号位不变,其他位全部取反。因为原码转补码的规则是:先取反,再加一
所以补码转原码的规则是:先减一,再取反。
减一操作:
1111 1110取反操作
1000 0001 = -1
~1步骤
步骤1:首先计算出1的补码,即它本身
步骤2:因为1的补码是负数,所以要还原其原码在输出;
因为原码转补码的规则是:先取反,再加一
所以补码转原码的规则是:先减一,再取反。
步骤1:首先计算出1的补码,即它本身
1的原码的补码是他本身:
0000 0001步骤2:因为1的补码是负数,所以要还原其原码在输出;
~1的反码:即所有位数,按位取反
1111 1110如果要输出打印,此时编译器发现其为最高位为1,是个负数,负数在计算机里面是用补码存储的,所以此时计算机认为这个1111 1110是补码,它要转换成原码输出,于是先减去1,除了符号位不变,其他位全部取反。减一操作:
1111 1101取反操作
1000 0010 = -2
~(-1)步骤
步骤1:首先计算出-1的补码(因为负数在计算机中以补码形式存在)
步骤2:再对-1的补码按位取反
步骤1:首先计算出-1的补码
-1的原码:
1000 0001-1的反码:即按位取反(负号不变)
1111 1110加一
1111 1111步骤2:再对-1的补码按位取反,包括符号位
~(1111 1111) =0000 0000 = 0 ~(-2)步骤
步骤1:首先计算出-2的补码因为负数在计算机中以补码形式存在)
步骤2:再对-2的补码按位取反
步骤1:首先计算出-2的补码因为负数在计算机中以补码形式存在)
-2的原码:
1000 0010-2的反码:即按位取反(负号不变)
1111 1101加一
1111 1110步骤2:再对-2的补码按位取反
0000 0001 = 1
<2>.代码示例二:按位取反参与多项运算
#include <stdio.h> int flag = 0x104; //0000 0001 0000 0100 int flag2 = 0x04;printf("flag2 = %#x\n",flag2);printf("~flag2 = %#x\n",~flag2);int b = flag & ~flag2;printf("b = %#x\n",b);return 0;
}打印:
flag2 = 0x4
~flag2 = 0xfffffffb
b = 0x100求flag & ~flag2
1.flag = 0x104
二进制原码:
0000 0001 0000 0100 2.flag2 = 0x04
二进制原码:
0000 0000 0000 0100~flag2(按位取反):
1111 1111 1111 1011flag与上flag2的反码0000 0001 0000 0100 1111 1111 1111 1011
= 0000 0001 0000 0000 = 0x100所以b = 0x100,和计算机打印的一样。
相关文章:
)
C语言之按位取反~(七十一)
计算机存储数据基本知识计算机中二进制数包括(正数和负数)是以补码形式存储。符号位:补码的最左侧首位是符号位,0表示正数,1表示负数。二进制有三种形式:原码、反码、补码。正数的补码和反码:是…...

C# 委托
Action 在 C# 中,Action 是一个预定义的委托类型,表示一个不带参数和返回值的方法。它的定义如下: public delegate void Action();Action 委托可以用于表示任何没有参数和返回值的方法。例如: // 定义一个不带参数和返回值的方…...
)
leetcode究极刷题笔记(11~15)
(11)盛最多水的容器(中等) 实现思路: 定义两个指针(a,b),分别指向数组的前后位置,如果此时a的值小于b的话,就将a右移一位,如果此时b指向的值小于…...

【C语言】一篇带你从零了解 枚举
文章目录什么是枚举枚举类型的定义枚举的优点枚举的使用什么是枚举 枚举是 C 语言中的一种基本数据类型 可以让数据更简洁,更易读。 枚举顾名思义就是 一 一 列举。 把可能的取值 一 一列举。 比如我们现实生活中: 一周的星期一到星期日是有限的7天&…...
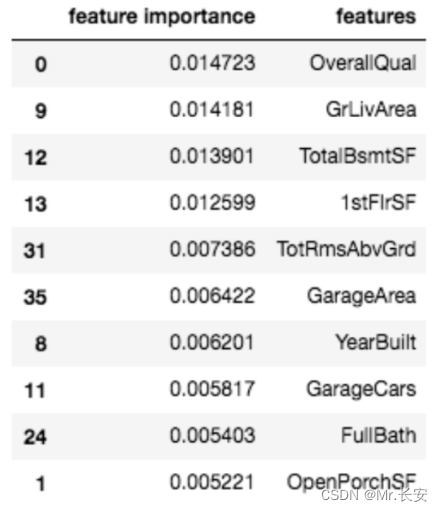
用Pytorch搭建一个房价预测模型
本文参加新星计划人工智能(Pytorch)赛道:https://bbs.csdn.net/topics/613989052 目录 一、项目介绍 二、准备工作 三、实验过程 3.1数据预处理 3.2拆分数据集 3.3构建PyTorch模型 3.3.1.数据转换 3.3.2定义模型架构 3.3.3定义损失准则和优化器 3.3.4创建…...

《Netty》从零开始学netty源码(十五)之ServerSocketChannel
在NioServerSocketChannel中调用newChannel方法创建java原生的channel,过程如下: ServerSocketChannel是一个抽象类,WEPollSelectorProvider调用openServerSocketChannel方法创建的是它的实现类ServerSocketChannelImpl,类结构如下…...
Java stream性能比较
环境 Ubuntu 22.04IntelliJ IDEA 2022.1.3JDK 17CPU:8核 ➜ ~ cat /proc/cpuinfo | egrep -ie physical id|cpu cores physical id : 0 cpu cores : 1 physical id : 2 cpu cores : 1 physical id : 4 cpu cores : 1 physical id : 6 cpu cores : 1 physical id …...

【数据结构与算法】设计循环队列
文章目录👑前言如何设计循环队列设计循环队列整体的代码📯写在最后👑前言 🚩前面我们 用队列实现了一个栈 ,用栈实现了一个队列 ,相信大家随随便便轻松拿捏,而本章将带大家上点难度,…...

最新版!国内IT软件外包公司汇总~
金三银四已经过去一半,再过几个月又将迎来毕业季,大家有没有找到心仪的工作机会呀?有很多同学说今年的金三银四似乎不存在了。小李:今年的金三银四变成了铜三铁四,不断地投递又不断地造拒。小王:大量已读不…...

MySQL的COUNT语句,竟然都能被面试官虐的这么惨!?
关于数据库中行数统计,无论是MySQL还是Oracle,都有一个函数可以使用,那就是COUNT 但是,就是这个常用的COUNT函数,却暗藏着很多玄机,尤其是在面试的时候,一不小心就会被虐。不信的话请尝试回答下…...
数位DP 详解及其案例实战 [模板+技巧+案例]
零. 案例引入 1.案例引入 leetcode233. 数字 1 的个数 给定一个整数 n,计算所有小于等于 n 的非负整数中数字 1 出现的个数。 输入:n 13 输出:6 2.暴力解 对于上述的案例,暴力解肯定是可行的,但时间复杂度较高,对…...
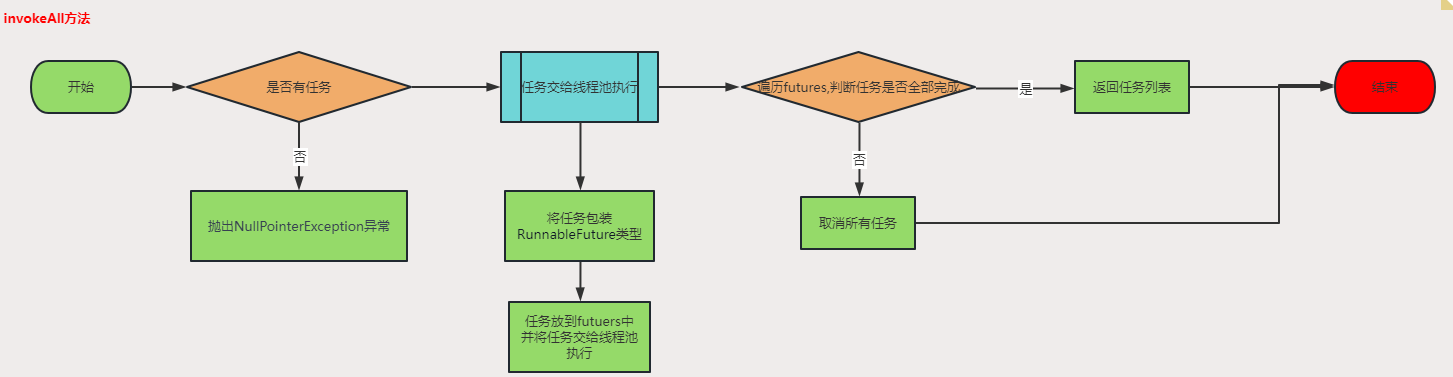
并发编程(六)—AbstractExecutorService源码分析
一、AbstractExecutorService简介AbstractExecutorService是一个抽象类,实现了ExecutorService接口,提供了线程池的基本实现。它是Java Executor框架的核心类,提供了线程池的基本操作,如提交任务、管理线程池、执行任务等。自定义…...

015行为型-职责链模式
目录定义标准模式实现:职责链变体使用链表实现使用数组实现应用场景日志输出spring过滤器spirng 拦截器mybatis动态sql定义 责链模式是一种设计模式,其目的是使多个对象能够处理同一请求,但是并不知道下一个处理请求的对象是谁。它能够解耦请…...
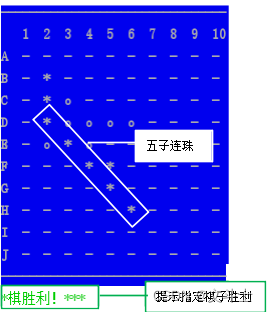
python例程:五子棋(控制台版)程序
目录《五子棋(控制台版)》程序使用说明程序示例代码可执行程序及源码下载路径《五子棋(控制台版)》程序使用说明 在PyCharm中运行《五子棋(控制台版)》即可进入如图1所示的系统主界面。 图1 游戏主界面 具…...

leveldb的Compaction线程
个人随笔 (Owed by: 春夜喜雨 http://blog.csdn.net/chunyexiyu) 1. leveldb的Compaction全局线程 在leveldb中,有一个全局的后台线程BGThread,用于数据库的MinorCompact与MajorCompact。 重点关注“全局线程”: 这个标识着无论一个进程打开…...

邪恶的想法冒出,立马启动python实现美女通通下
前言 嗨喽~大家好呀,这里是魔王呐 ❤ ~! 完整源码、python资料: 点击此处跳转文末名片获取 当我在首页刷到这些的时候~ 我的心里逐渐浮现一个邪念:我把这些小姐姐全都采集,可以嘛? 答案当然是可以的~毕竟就我这技术,…...

蓝桥杯刷题冲刺 | 倒计时18天
作者:指针不指南吗 专栏:蓝桥杯倒计时冲刺 🐾马上就要蓝桥杯了,最后的这几天尤为重要,不可懈怠哦🐾 文章目录0.知识点1.乳草的入侵今天写 搜索题 0.知识点 DFS 设计步骤 确定该题目的状态(包括边…...

经典算法面试题——Java篇-附带赠书活动,评论区随机选取一人赠书
目录 一.图书推荐 二.说一下什么是二分法?使用二分法时需要注意什么?如何用代码实现? 三.什么是插入排序?用代码如何实现? 四.什么是冒泡排序?用代码如何实现? 五.什么是斐波那契数列&#…...

支持RT-Thread最新版本的瑞萨RA2E1开发板终于要大展身手了
支持RT-Thread最新版本的瑞萨RA2E1开发板终于要大展身手了 熟悉RT-Thread和瑞萨MCU的朋友都知道,当前RT-Thread仓库的主线代码是不支持RA2E1这个BSP的。刚好,最近我在联合瑞萨推广一个叫《致敬未来的攻城狮计划》,使用的就是RA2E1开发板&…...

【C语言进阶】 12. 假期测评①
day01 1. 转义字符的判断 以下不正确的定义语句是( ) A: double x[5] {2.0, 4.0, 6.0, 8.0, 10.0}; B: char c2[] {‘\x10’, ‘\xa’, ‘\8’}; C: char c1[] {‘1’,‘2’,‘3’,‘4’,‘5’}; D: int y[53]{0, 1, 3, 5, 7, 9}; 【答案解析】 B 本…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...
