算法日记day 39(动归之打家劫舍)
一、打家劫舍1
题目:
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1] 输出:4 解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入:[2,7,9,3,1] 输出:12 解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。偷窃到的最高金额 = 2 + 9 + 1 = 12 。
思路:
明确dp数组的含义,本题dp数组的含义为包含前 i 个元素(包含 i)所得的最大值为dp[i],分别有两种情况
第一种
要第 i 个元素:此时第 i-1 个元素不能要,只能从第 i-2个元素拿,表达为dp[i-2]+nums[i]
第二种
不要第 i 个元素:此时应该从第 i-1 个元素选择拿与不拿,表达为dp[i-1]
因此可得递推式为
dp[i] +=max(dp[i-1],dp[i-2]+nums[i])
代码:
public int rob(int[] nums) {// 如果输入数组为空或者长度为0,则没有房子可打劫,返回0if (nums == null || nums.length == 0)return 0;// 如果只有一个房子,只能打劫这个房子,直接返回其金额if (nums.length == 1)return nums[0];// dp 数组用来存储到第 i 个房子时能偷到的最大金额int[] dp = new int[nums.length + 1];// 初始化 dp 数组dp[0] = nums[0]; // 偷第一个房子时的最大金额dp[1] = Math.max(nums[0], nums[1]); // 偷第一个或第二个房子中金额较大的一个// 从第三个房子开始计算for (int i = 2; i < nums.length; i++) {// dp[i] 表示偷到第 i 个房子时的最大金额// 选择偷第 i 个房子的情况,应该加上之前能偷到的最大金额(即 dp[i-2]);// 或者选择不偷第 i 个房子,则最大金额等于 dp[i-1]dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);}// 最终结果是到最后一个房子的最大金额return dp[nums.length - 1];
}
-
边界条件处理:
if (nums == null || nums.length == 0) return 0;- 处理输入为空或没有房子的情况,直接返回
0。
- 处理输入为空或没有房子的情况,直接返回
if (nums.length == 1) return nums[0];- 处理只有一个房子的情况,直接返回那个房子的金额。
-
动态规划数组初始化:
int[] dp = new int[nums.length + 1];- 创建一个大小为
nums.length + 1的数组dp。dp[i]表示偷到第i个房子时的最大金额。
- 创建一个大小为
dp[0] = nums[0];- 如果只有第一个房子,那么偷这个房子的钱就是
dp[0]。
- 如果只有第一个房子,那么偷这个房子的钱就是
dp[1] = Math.max(nums[0], nums[1]);- 比较前两个房子的金额,取较大的一个,因为只能选择偷第一个房子或第二个房子中的一个。
-
状态转移:
for (int i = 2; i < nums.length; i++)- 从第三个房子开始计算。
dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);- 选择偷第
i个房子的情况:此时的金额为dp[i - 2] + nums[i]。 - 不偷第
i个房子的情况:此时的金额为dp[i - 1]。 - 取两者中的最大值作为
dp[i]的值。
- 选择偷第
-
返回结果:
return dp[nums.length - 1];- 最终返回
dp数组最后一个元素,即偷到最后一个房子时能获得的最大金额。
- 最终返回
二、打家劫舍2
题目:
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
示例 1:
输入:nums = [2,3,2] 输出:3 解释:你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。
示例 2:
输入:nums = [1,2,3,1] 输出:4 解释:你可以先偷窃 1 号房屋(金额 = 1),然后偷窃 3 号房屋(金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。
示例 3:
输入:nums = [1,2,3] 输出:3
思路:
与打家劫舍1不同的是,题中将nums数组连接成一个环形结构,因此存在三种情况
第一种:选择首元素和中间所有元素,尾元素则不能选取
第二种:选择尾元素和中间所有元素,首元素不能选择
第三种:首位元素均不选择,只选择中间的元素
第三种情况可以包含在第一种情况中,在第一种情况中如果我们不拿首元素即为第三种情况
因此需要讨论第一种和第二种情况中哪个可以拿到更多,取两种情况最大值
代码:
public int rob(int[] nums) {// 如果输入数组为空或长度为0,则没有房子可打劫,返回0if (nums == null || nums.length == 0)return 0;int len = nums.length;// 如果只有一个房子,只能打劫这个房子,直接返回其金额if (len == 1)return nums[0];// 计算两种情况的最大值// 1. 从第一个房子到倒数第二个房子(不打劫最后一个房子)// 2. 从第二个房子到最后一个房子(不打劫第一个房子)return Math.max(robAction(nums, 0, len - 1), robAction(nums, 1, len));
}int robAction(int[] nums, int start, int end) {int x = 0; // 代表上一个房子之前的最大金额int y = 0; // 代表上一个房子的最大金额int z = 0; // 当前房子的最大金额// 遍历从 start 到 end(不包括 end)范围内的房子for (int i = start; i < end; i++) {y = z; // 当前的最大金额之前的最大金额z = Math.max(y, x + nums[i]); // 当前房子的最大金额是之前最大金额和加上当前房子金额后的最大值x = y; // 更新 x 为之前的最大金额}return z; // 返回当前房子的最大金额
}
三、打家劫舍3
题目:
小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为 root 。
除了 root 之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ,房屋将自动报警。
给定二叉树的 root 。返回 在不触动警报的情况下 ,小偷能够盗取的最高金额 。
示例 1:

输入: root = [3,2,3,null,3,null,1] 输出: 7 解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7
示例 2:

输入: root = [3,4,5,1,3,null,1] 输出: 9 解释: 小偷一晚能够盗取的最高金额 4 + 5 = 9
思路:
本题为树形结构,采用后序遍历的方法,相邻节点之间不能同时拿取,在定义dp数组时分别有两种情况,分别是dp[0],代表在不拿当前节点的情况下所偷取的最大金额,dp[1]代表在拿当前节点的情况下所偷取的最大金额
若不拿取当前节点的,则需要在其左右子节点中判断是否要拿去,若拿当前节点,则应跳过其左右子节点去判断是否拿取下一层的金额
代码:
public int rob(TreeNode root) {// 调用辅助函数 robAction 计算最大可窃取金额int[] res = robAction(root);// 返回 robAction 的结果中最大的值return Math.max(res[0], res[1]);
}int[] robAction(TreeNode root) {// res[0]: 不打劫当前房子的最大金额// res[1]: 打劫当前房子的最大金额int res[] = new int[2];// 如果当前节点为空,返回 [0, 0]if (root == null)return res;// 递归计算左子树和右子树的结果int[] left = robAction(root.left);int[] right = robAction(root.right);// res[0] 是不打劫当前房子的最大金额// 选择打劫左右子树中最大的金额res[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);// res[1] 是打劫当前房子的最大金额// 当前房子的值加上左右子树不打劫的情况res[1] = root.val + left[0] + right[0];// 返回当前节点的结果return res;
}
-
rob方法:- 参数:
TreeNode root表示二叉树的根节点。 - 功能:计算从根节点开始的最大可窃取金额。
- 步骤:
- 调用
robAction方法获取当前树的最大可窃取金额。 res数组的两个元素分别表示打劫和不打劫根节点的情况。- 使用
Math.max选择这两种情况中的较大值作为最终结果并返回。
- 调用
- 参数:
-
robAction方法:- 参数:
TreeNode root表示当前处理的节点。 - 返回值:一个数组
res,其中res[0]表示不打劫当前节点时的最大可窃取金额,res[1]表示打劫当前节点时的最大可窃取金额。 - 步骤:
- 初始化
res数组为[0, 0],表示当前节点为空时的结果。 - 如果当前节点为
null,直接返回[0, 0],因为没有任何价值可以打劫。 - 递归调用
robAction方法处理左子树和右子树,分别将结果存储在left和right中。 -
res[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]); - 在这种情况下,可以选择打劫或不打劫左右子树,从而得到最大金额。
res[1] = root.val + left[0] + right[0]; - 在这种情况下,打劫当前节点的值,并且左右子树的最大金额必须是它们分别不打劫的情况。
- 返回
res数组,包含当前节点的打劫和不打劫情况的最大金额。
- 初始化
- 参数:
今天的学习就到这里
相关文章:

算法日记day 39(动归之打家劫舍)
一、打家劫舍1 题目: 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。…...

Vue 生命周期详解含demo、面试常问问题案例
Vue 生命周期详解、面试常问问题案例 含 demo 文章目录 Vue 生命周期详解、面试常问问题案例 含 demo一、Vue 生命周期是什么二、Vue 中如何使用生命周期钩子1. **beforeCreate**2. **created**3. **beforeMount**4. **mounted**5. **beforeUpdate**6. **updated**7. **beforeD…...

表单自定义规则的校验
在 Vue 3 中使用 Element Plus 的表单组件进行自定义规则的校验非常方便。Element Plus 提供了 ElForm 和 ElFormItem 组件,它们内置了表单验证的功能。下面我将详细介绍如何使用 Element Plus 进行自定义规则的校验。 创建表单及规则 首先,你需要创建…...

JVM 有哪些垃圾回收算法(回收机制)?
JVM 有哪些垃圾回收算法(回收机制)? 标记-清除算法 在Java虚拟机中,标记-清除算法是一种用于垃圾回收的算法。它分为两个阶段:标记阶段和清除阶段。 在标记阶段,垃圾收集器会遍历堆内存中的所有对象&…...

2024年高教社杯数学建模国赛A题思路解析+代码+论文
2024年高教社杯全国大学生数学建模竞赛(以下简称国赛)将于9月5日晚6时正式开始。 下文包含:2024国赛思路解析、国赛参赛时间及规则信息说明、好用的数模技巧及如何备战数学建模竞赛 C君将会第一时间发布选题建议、所有题目的思路解析、相…...
Linux中yum、vim、gcc/g++的使用
目录 一、Linux 软件包管理器 yum 什么是软件包 关于 rzsz 查看软件包★ 如何安装软件★ 如何卸载软件★ Linux 开发工具 二、Linux编译器-vim使用 vim的基本概念 vim的基本操作 vim正常模式命令集 vim末行模式命令集 vim操作总结 如果在vim界面不小心按了Ctrl …...

基于模糊神经网络的金融序列预测算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.本算法原理 5.完整程序 1.程序功能描述 基于模糊神经网络的金融序列预测算法matlab仿真,根据序列的MAD,RSI,KD等指标实现序列的预测和最终收益分析。 2.测试软件版本以及运行结果展示 MATLAB2022A版本…...

STM32 HAL库常用功能封装
关中断 /*** brief 关闭所有中断(但是不包括fault和NMI中断)* param 无* retval 无*/ void sys_intx_disable(void) {__ASM volatile("cpsid i"); }开中断 /*** brief 开启所有中断* param 无* retval 无*/ void sys_intx_enabl…...

golang zap日志库 打印日志时显示的源文件始终是同一个问题解决方法 zap.Option函数可选项 zap.AddCallerSkip(1) 使用示例
这种情况一般出现在我们对zap日志库进行二次封装的情况下, 在打印日志的时候的源文件非我们期望的文件,如下 原因分析 出现这个问题的原因是zap函数内部在调用 runtime.Caller 时的skip层级不对了,因为我们进行了二次封装,所以za…...

BL196MQTT远程IO模块助力智能楼宇自动化升级
在智能楼宇自动化领域,每一个细节的优化都能带来整体效率与舒适度的显著提升。钡铼技术的BL196MQTT远程IO模块,以其卓越的灵活性和强大的性能,正在成为这一领域中推动楼宇自动化升级的关键力量。 钡铼技术IOy系列:创新与灵活性的…...
)
【面试宝典】Java面向对象面试题总结(上)
一、重写和重载 在Java中,重写(Override)和重载(Overload)是面向对象编程中两个非常重要的概念,它们都与方法的定义和调用有关,但两者有着本质的区别。 1、重写(Overrideÿ…...

如何运用独特的产业运营体系打造一流的数字媒体产业园
如何运用独特的产业运营体系打造一流的数字媒体产业园 2024-08-15 17:37树莓集团 在数字经济蓬勃发展的今天,数字媒体产业作为其中的重要一环,正展现出巨大的潜力和活力。而如何运用独特的产业运营体系,打造一流的数字媒体产业园࿰…...

安全基础学习-SHA-256
SHA-256 是一种密码学哈希函数,是 SHA-2(Secure Hash Algorithm 2)家族的一部分。它被广泛用于数据完整性验证、数字签名以及密码存储等领域。 1、SHA-256的原理 SHA-256 生成一个固定长度为 256 位(32 字节)的哈希值。无论输入数据的大小或类型,输出的哈希值始终是 25…...

Redis中Big Key该如何解决?
目录 1、Big Key的产生 2、BigKey场景分析 3、Big Key的危害 4、检测 BigKey 5、解决 BigKey 问题 Big Key拆分 (1)按时间/业务拆分 (2)按哈希(Hash)拆分 (3)按前缀树拆分…...

基于springboot的实习管理系统
TOC springboot207基于springboot的实习管理系统 绪论 1.1研究背景与意义 信息化管理模式是将行业中的工作流程由人工服务,逐渐转换为使用计算机技术的信息化管理服务。这种管理模式发展迅速,使用起来非常简单容易,用户甚至不用掌握相关的…...
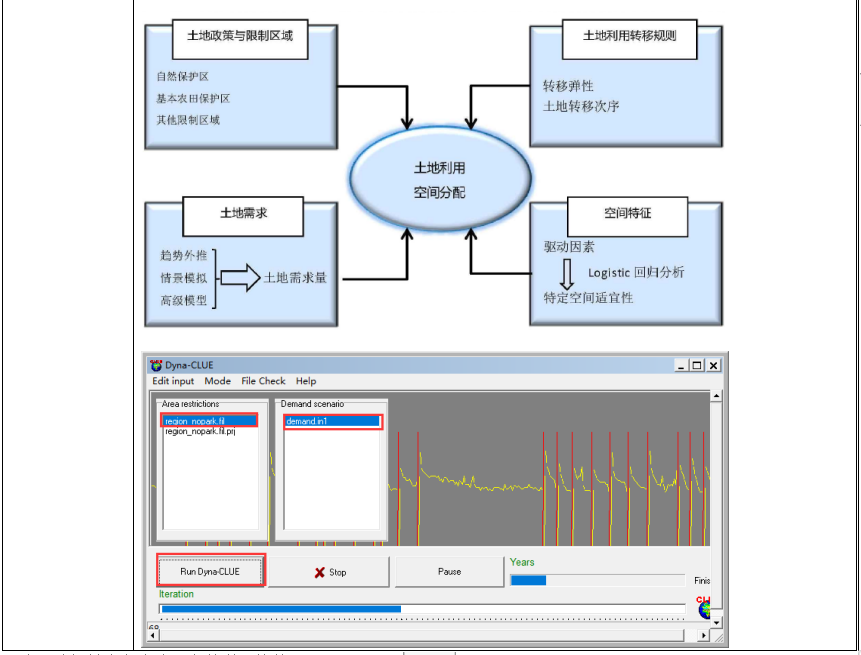
土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测
土地利用/土地覆盖数据是生态、环境和气象等领域众多模型的重要输入参数之一。基于遥感影像解译,可获取历史或当前任何一个区域的土地利用/土地覆盖数据,用于评估区域的生态环境变化、评价重大生态工程建设成效等。借助CLUE模型,实现对未来土…...

Rust 之环境搭建
前言 Rust 是一种现代的系统级编程语言,以其内存安全性、高性能和简洁的语法而著称。本文将介绍如何在不同操作系统上搭建 Rust 开发环境,并配置好基础工具,使您能够快速开始 Rust 编程。 1. 安装 Rust Rust 官方推荐使用 rustup 工具来管…...

基于微信小程序地图实现点位标注、覆盖物、地图聊天
目录 小程序部分map标签的使用获取用户经纬度并转换地址地图点击事件覆盖物标注点击并实现弹窗交互数据库及接口部分数据库表结构设计API搭建小程序接口使用注意事项wx.getLocation深入控制地图小程序部分 map标签的使用 创建小程序的步骤这里不再重复赘述,在wxml页面中放一个…...

xxl-job的分片广播+单播
1 介绍一下xxl-job XXL-JOB 是一个分布式任务调度平台,旨在为分布式应用系统提供开箱即用的调度解决方案。它非常易于使用,并具有很高的可扩展性。以下是 XXL-JOB 的详细介绍,包括其核心功能、架构设计、主要组件及其应用场景。 核心功能 简…...

情感分类代码
在进行自然语言处理中的情感分类时,通常需要准备以下几方面的内容: 1. **数据集**:高质量的标注数据集是关键,包括正面、负面和中性情感标记的文本。 2. **情感词典**:可用的情感词典,如SentiWordNet&…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...
