微信答题小程序产品研发-后端开发
在开发答题小程序的后端服务和数据库设计时,需要考虑API的设计、数据库模型的构建以及数据的安全性和一致性。
这里我采用了云开发,后端语言是Node,数据库是NoSql,然后我简单整理了各个功能模块的后端开发概要和数据库设计。

1. 首页
(1)API:提供一个API接口用于获取首页信息,如轮播图、公告等。
(2)数据库:设计一个`homepage`表,存储首页相关的数据。
2. 轮播图
(1)API:创建一个API接口用于获取轮播图数据。
(2)数据库:设计一个`banners`表,包含字段如`id`, `image_url`, `link`, `description`, `status`等。
3. 公告
(1)API:创建API接口用于发布、获取和更新公告信息。
(2)数据库:设计一个`announcements`表,包含字段如`id`, `title`, `content`, `publish_date`, `status`等。
4. 微信授权登录
(1)API:实现微信授权登录的API接口,与微信服务器进行交互获取用户信息。
(2)数据库:设计一个`users`表,包含字段如`id`, `openid`, `nickname`, `avatar_url`, `last_login`等。
5. 题库练习
(1)API:创建API接口用于获取题库分类、题目列表、题目详情等。
(2)数据库:
- `categories`表,存储题库分类信息。
- `questions`表,存储题目信息,字段如`id`, `category_id`, `content`, `options`, `answer`, `difficulty`等。
6. 出题考试
(1)API:实现API接口用于创建、发布和获取考试信息。
(2)数据库:
- `exams`表,存储考试信息,字段如`id`, `title`, `description`, `start_time`, `end_time`等。
- `exam_questions`表,存储考试与题目的关联信息。
7. 错题集
(1)API:创建API接口用于记录和获取用户的错题信息。
(2)数据库:设计一个`wrong_questions`表,包含字段如`id`, `user_id`, `question_id`, `wrong_time`等。
8. 答题历史
(1)API:实现API接口用于记录和获取用户的答题历史。
(2)数据库:设计一个`answer_records`表,包含字段如`id`, `user_id`, `exam_id`, `score`, `answer_time`等。
9. 收藏
(1)API:创建API接口用于管理用户的收藏题目。
(2)数据库:设计一个`favorites`表,包含字段如`id`, `user_id`, `question_id`, `favorite_time`等。
10. 个人中心
(1)API:实现API接口用于获取和更新用户的个人信息。
(2)数据库:`users`表中已经包含了个人中心所需的基本信息。
小结:
在实际开发过程中,需要确保前后端数据交互的顺畅。进行代码的测试和调试,确保后端服务的稳定性和性能。此外,还有其他注意事项:
(1)安全性:确保所有API接口都进行适当的身份验证和授权检查。
(2)数据一致性:使用事务确保数据库操作的原子性。
(3)性能优化:对数据库进行索引优化,确保查询效率。
(4)错误处理:合理处理可能出现的错误,并返回清晰的错误信息。
(5)API文档:编写详细的API文档,方便前端开发人员理解和使用。

相关文章:

微信答题小程序产品研发-后端开发
在开发答题小程序的后端服务和数据库设计时,需要考虑API的设计、数据库模型的构建以及数据的安全性和一致性。 这里我采用了云开发,后端语言是Node,数据库是NoSql,然后我简单整理了各个功能模块的后端开发概要和数据库设计。 1. …...

回溯算法——LeetCode37 解数独
题目 力扣题目链接 思路 卡哥的思路,注意看他解释为什么是“二维回溯”。我的思路,类似y总解决 N 皇后问题时的第二种方法,即从左上到右下枚举棋盘的每个位置。 至于为什么与 N 皇后问题不一样,我认为是因为它每一行不止放一个…...

【CPP】继承语法详解与菱形继承
关于我: 睡觉待开机:个人主页 个人专栏: 《优选算法》《C语言》《CPP》 生活的理想,就是为了理想的生活! 作者留言 PDF版免费提供:倘若有需要,想拿我写的博客进行学习和交流,可以私信我将免费提供PDF版。…...

数据结构(6.2_1)——领接矩阵法
图的存储——邻接矩阵法 邻接矩阵(Adjacency Matrix)是一种使用二维数组来表示图的方法。在这种表示法中,矩阵的行和列都对应图的顶点。 特点 对于无向图,如果顶点i与顶点j之间有边,则矩阵的第i行第j列(…...

诈骗未成功是否构成犯罪?
诈骗未成功不一定构成犯罪。在刑法上,构成诈骗罪需要满足特定的构成要件,包括有非法占有的目的、实施了虚构事实或隐瞒真相的行为、对方因此陷入错误认识并处分财产、行为人或第三方取得财产、被害人遭受财产损失。如果诈骗行为未能成功,即被…...
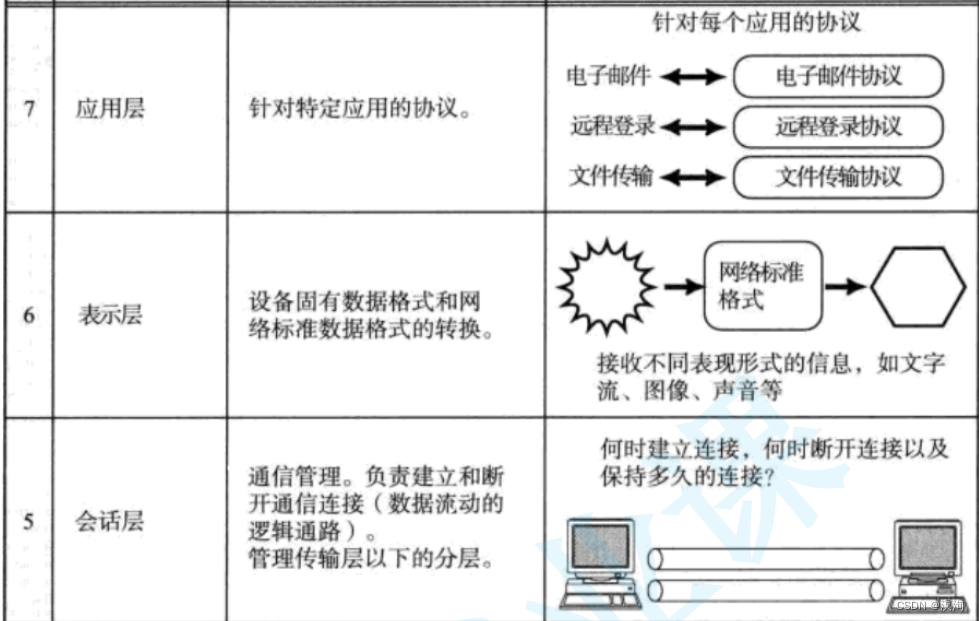
网络协议栈应用层的意义(内含思维导图和解析图通俗易懂超易理解)
绪论: “节省时间的方法就是全力以赴的将所要做的事情完美快速的做完,不留返工重新学习的时间,才能省下时间给其他你认为重要的东西。” 本章主要讲到OSI网络协议栈中的应用层的作用和再次在应用层的角度理解协议的具体意义,以及…...

【NXP-MCXA153】i2c驱动移植
介绍 I2C总线由飞利浦公司开发,是一种串行单工通信总线,它主要用于连接微控制器和其他外围设备并在总线上的器件之间传送信息(需要指定设备地址);常见的i2c设备有EEPROM、触摸屏、各种IoT传感器、时钟模块等&#x…...

C++(11)类语法分析(2)
C(10)之类语法分析(2) Author: Once Day Date: 2024年8月17日 一位热衷于Linux学习和开发的菜鸟,试图谱写一场冒险之旅,也许终点只是一场白日梦… 漫漫长路,有人对你微笑过嘛… 全系列文章可参考专栏: 源码分析_Once-Day的博客-CSDN博客 …...
)
数字验证每日十问--(3)
深拷贝和浅拷贝的区别? 当只拷贝对象中的成员变量和声明的句柄时,称为浅拷贝。浅拷贝只把对象中的句柄复制了,却没有复制句柄b所指向的对象。这会导致复制后,a2中的句柄b 和 a1 中的句柄b指向同一个对象,如果a2中的句…...

22.给定 n 对括号,实现一个算法生成所有可能的正确匹配的括号组合
22. Generate Parentheses 题目 给定 n 对括号,编写一个函数生成所有可能的正确匹配的括号组合。 例如,当 n = 3 时,可能的组合集合为: ["((()))","(()())","(())()","()(())","()()()" ]题目大意 给出 n 代表生成…...

检测到目标URL存在http host头攻击漏洞
漏洞描述 修复措施 方法一: nginx 的 default_server 指令可以定义默认的 server 去处理一些没有匹配到 server_name 的请求,如果没有显式定义,则会选取第一个定义的 server 作为 default_server。 server { …...

C++奇迹之旅:手写vector模拟实现与你探索vector 容器的核心机制与使用技巧
文章目录 📝基本框架🌠 构造和销毁🌉vector()🌉vector(const vector& v)🌉vector(size_t n, const T& value T())🌉赋值拷贝构造:vector<T>& operator(vector<T> v)&a…...

018、钩子函数 mounted和beforeDestroy、父组件向子组件传递参数 props 的使用
文章目录 1、mounted 和 beforeDestroy1.1、mounted1.2、beforeDestroy 2、父组件向子组件传递参数 props2.1、子组件定义2.2、父组件调用子组件并传参 3、完整例子3.1、父组件 Tags.vue3.2、子组件 TagsMenu.vue3.3、效果图 1、mounted 和 beforeDestroy 1.1、mounted mount…...

xlnt在Windows中的dll,lib生成
前言 花了半天时间想要把xlnt 集成到VS2022 Cmake项目中,以我目前掌握的能力,Cmake语法对于我来说难懂,对于只是使用过Cmake编译MySQL,或是其他lib,dll库的小白来说,不应该为了显示自己能力多么出众,强行去配置一些程序内容。 生活中没有绝对的事情,有舍有得. https://github…...

【网络】私有IP和公网IP的转换——NAT技术
目录 引言 NAT工作机制编辑 NAT技术的优缺点 优点 缺点 个人主页:东洛的克莱斯韦克-CSDN博客 引言 公网被子网掩码划分为层状结构,一个公网IP的机器又可以用很多私有IP搭建内网。在日常生活场景中用的都是私有IP,例如手机,…...

java 面试 PDF 资料整理
“尊贵的求知者,作者特此献上精心编纂的Java面试宝典PDF,这份资料凝聚了无数面试精华与实战经验,是通往Java技术殿堂的钥匙。若您渴望在Java编程的求职之路上稳健前行,只需轻轻一点,完成这象征支持与认可的一键三联&am…...

初步认识Linux系统
前言 Linux系统具有许多优点,不仅系统性能稳定,而且是开源软件。其核心防火墙组件性能高效、配置简单,保证了系统的安全。在很多企业网络中,为了追求速度和安全,Linux不仅仅是被网络运维人员当作服务器使用,…...

JavaScript AI 编程助手
JavaScript AI 编程助手 引言 随着人工智能技术的飞速发展,编程领域也迎来了前所未有的变革。JavaScript,作为全球最流行的编程语言之一,其与AI的结合为开发者带来了巨大的便利和无限的可能性。本文将探讨JavaScript AI编程助手的定义、功能…...

达梦数据库的系统视图v$datafile
达梦数据库的系统视图v$datafile 达梦数据库的V$DATAFILE 是一个重要的系统视图,提供了有关数据库数据文件的信息。 V$DATAFILE 系统视图 V$DATAFILE 视图用于显示数据库中每一个数据文件的详细信息。通过查询这个视图,数据库管理员可以了解数据文件的…...

Triton/window安装: triton-2.0.0-cp310-cp310-win_amd64.whl文件
下面这个github仓: https://github.com/PrashantSaikia/Triton-for-Windows/tree/main 安装命令也很简单,下载到本地后运行: pip install triton-2.0.0-cp310-cp310-win_amd64.whl...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...
