旅行推销员问题的遗传算法中的完整子路线顺序交叉
摘要
旅行商问题(TSP)是许多著名的组合问题之一。TSP可以解释为很难找到从第一个城市出发,经过所有城市,然后返回起点的最短距离。在标准问题中,TSP通常用于确定新算法的效率。遗传算法是求解TSP问题的一种成功算法。遗传算法求解效率的关键机制是交叉算子。许多研究提出了新的交叉甚至改进的解决TSP的方法,包括其他相关问题。然而,solution quality是最重要的因素。本文提出了遗传算法的完全子图阶交叉(CSOX)来搜索TSP的解。CSOX采用订单交叉Order crossover(OX)原理,并将交叉扩展到主要涵盖质量解决方案的部分。值得注意的是,一个操作可以生成六个新的解决方案。这一结果增加了问题解决方案的多样性和质量,同时降低了计算时间。从三项研究中,将五种类型的交叉算子与CSOX进行了比较。实验总结结果表明,CSOX在解决方案质量和良好的计算时间方面优于所有方案。
引言
旅行商问题(TSP)是一个常见的组合优化问题,属于NP难问题。TSP问题旨在寻找前往不同城市的最短路径。这个问题的局限性在于每个城市只能访问一次。此外,一旦访问了所有城市,销售人员必须返回出发城市。TSP经常被应用于新算法的性能评估。
遗传算法(GA)是一种受生物启发的进化算法,可以很好地解决TSP问题。遗传算法通过模仿物种的进化和自然选择的思想来工作。因此,例如,身体状况良好的生物更有可能存活下来,并将这些良好的特征传递给下一代[1]。尽管遗传算法已经提出了很长时间,但最近许多研究中开发的新算法都是在遗传算法概念之后原型化的。此外,许多研究已经应用了遗传算法原理,并将其与其他算法相结合来解决一些问题[2]。遗传算法的运作始于以染色体形式表达的群体的一代。每个染色体或个体都包含基因,代表着问题可能解决方案的一个特征。然后,遗传算法评估基因适应度,选择并相应地提高解决方案的质量。
交叉算子是解决方案改进过程中的一个重要机制。交叉通常由两个个体或两个选定的父母的组合产生。重组在父母之间进行信息交换。因此,获得的后代将具有其父母的特征。根据组合技术的不同,每个后代都会有所不同。
保持种群多样性是交叉设计的挑战之一,因为它可以防止过早收敛或陷入局部最优。此外,多样性通常会增加搜索新解决方案空间的可能性,并带来更好的解决方案质量。然而,更高的多样性是浪费时间。因此,交叉算子应该给出适当的分集,以有效地解决过早收敛问题[3]。
目前,GA有许多交叉算子。请注意,部分映射交叉(PMX)和顺序交叉(OX)是各种研究中经常发现的两种算子,用于比较和提高算法性能。PMX是使用最广泛的基于置换的交叉算子。在PMX中,第一个亲本的基因被映射到第二个亲本的遗传基因上,剩下的信息被交换。相比之下,OX通过选择第一个亲本的基因并维持第二个亲本基因的相对顺序来产生后代。尽管一些研究人员指出,PMX比OX表现出更好的解决方案搜索,但它需要更多的计算时间[4][5]。
最佳顺序交叉(BOX)是另一种将双亲和全局最佳个体之间的信息相结合的技术。该技术优于许多现有的置换交叉方案[6]。
改进(IPMX)是对PMX技术的重新设计,以减少计算时间而不影响解决方案质量。IPMX、PMX和另外两种方法进行了并行评估。最佳解决方案来自IPMX[7]。
同时,另一个选择了两个以上父母来增加多样性的运营商被称为多父母交叉。样本是多父部分映射交叉(MPPMX)和多父顺序交叉(MPOX)
因此,本研究提出了一种新的交叉算子,利用双亲产生六个后代,以按时保持种群的多样性。同时,来自父母的优秀信息将被选择传递给后代。
二、GA代表TSP
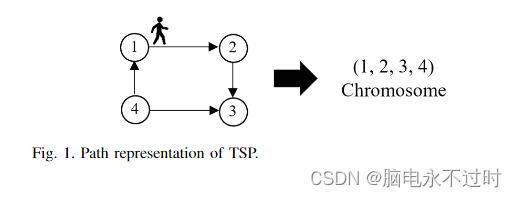
本节描述了用于解决TSP问题的遗传算法。本文对遗传算法的每一个过程进行了推广。A.染色体代表一个数字代表每个城市的名字。访问每个城市的路线或顺序是TSP的染色体编码。当一个销售人员访问所有城市时,他必须返回出发城市。路线示例1→2.→3.→4.→1可以用(1,2,3,4)表示,如图1所示。
B、 遗传算法过程在本文中,可以通过以下步骤定义一个简单的遗传算法。详情如下。第一步,创建一个由n条染色体组成的初始群体。第二步,评估每个染色体的适合度。步骤3,根据最佳适应度值选择n条染色体的群体。步骤4,使用交叉算子随机选择两个亲本来创建后代。步骤5,应用具有低随机概率的变异算子。第6步,将新的后代添加到种群中,然后进入第2步。最后,如果代数满足,则终止。步骤2中的适合度是所有城市之间旅行成本的总和。然而,TSP是一个最小化问题,因此适应度函数为F(x)=1/F(x),其中F(x)是目标函数。步骤4-5中使用的GA运算符将在第四节中讨论。
三、提出的交叉算子
本文针对TSP问题,提出了遗传算法中的完全子任务交叉(CSOX)。CSOX采用订单交叉(OX)原理,并扩展交叉位置以覆盖解决方案的适当组件。此外,还提出了保留基因序列和交换良好信息的建议。然而,CSOX在执行时间合适的情况下最多可以生成六个后代。CSOX程序在算法1中进行了描述。在图2中,OX的原理用于交换基因以产生后代。生成的子代的质量在GA工作周期的同时得到改善。通常,被选为首选旅行目的地的城市有可能提高解决方案的质量,因为这些城市通常位于起点和最后一个城市附近。


因此,将选择排名第一和最后的城市,以进一步传播给具有这一概念的后代。
四、实验和结果
在本节中,实验分为四个部分,以评估CSOX与TSP实例中其他交叉的效果。本研究采用了TSPLIB,这是一个著名的TSP实例库(可从http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/)。
实验1-3是与关于解决方案的其他文献相比的CSOX功效评估。 travel costs函数衡量解决方案的质量,最优解决方案的 travel costs最低。根据对比研究调整各实验的参数设置。此外,各文献中使用的TSP实例并不相等。只有在所有实例中发现相同的实例才会被选中。例如,eil51、st70,实例名称上的数字表示城市的数量。最后,实验4是与广泛已知的交叉相比的CSOX收敛性评估。所提出的算法用python编程语言实现,并在装有Windows 10操作系统、2.60 GHz Intel i7处理器和8 GB RAM的笔记本电脑上运行。
实验一:
本实验将CSOX的性能与BOX和OX[6]进行了比较。参数设置和比较结果分别如表I-II所示:
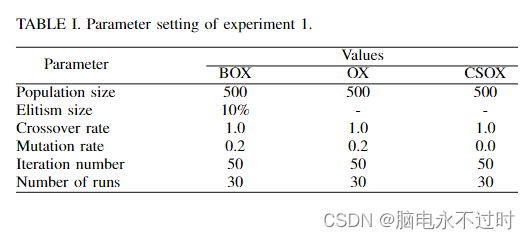
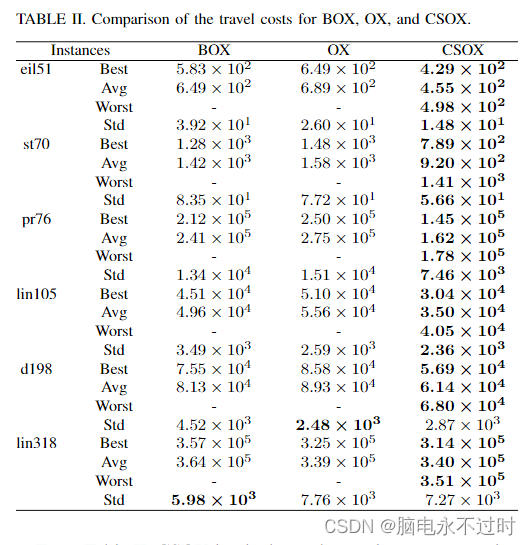
从表II可以看出,CSOX在所有情况下都给出了比BOX和OX更好的最佳值、平均值。尽管BOX和OX没有显示最差值,但CSOX的最差值优于BOX和OX的最佳值。
B.实验2
本实验比较了CSOX与PMX和IPMX[7]在解决方案质量和计算时间方面的性能。参数设置和比较结果分别如表III-IV所示。
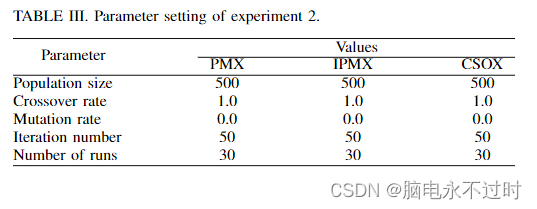
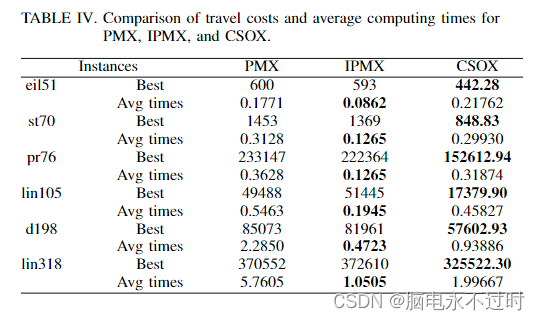
在表IV中,PMX和IPMX在溶液质量方面表现出相似之处。然而,IPMX工作速度更快,而CSOX提供的解决方案质量比PMX和IPMX更好。在计算时间方面,CSOX比PMX消耗的时间更少,并且提供了更好的解决方案质量。
C.实验3
本实验比较了CSOX与MPPMX和MPOX的性能。不幸的是,对上述发布的实验数据进行了检查。发现数据不准确,并且偏离了TSP实例的标准解,因此无法进行比较。因此,本实验将CSOX与MPPMX[8]进行了比较。参数设置和比较结果分别如表V-VI所示。
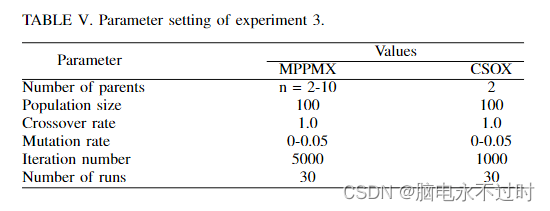
这个实验使用了交换突变以及MMPMX。如表VI所示,基于参考数据,MPPMX疗效测试仅使用了五个实例。CSOX的突变率为0.03,在所有情况下都比MPPMX的结果更好。
D.实验4
最后的实验比较了CSOX、OX和PMX的收敛性。不幸的是,这个实验无法与以前实验中的算法进行比较,以防止结果出现错误。参数设置如下:种群规模=500,交叉率=1.0,突变率=0.0,运行次数=30。
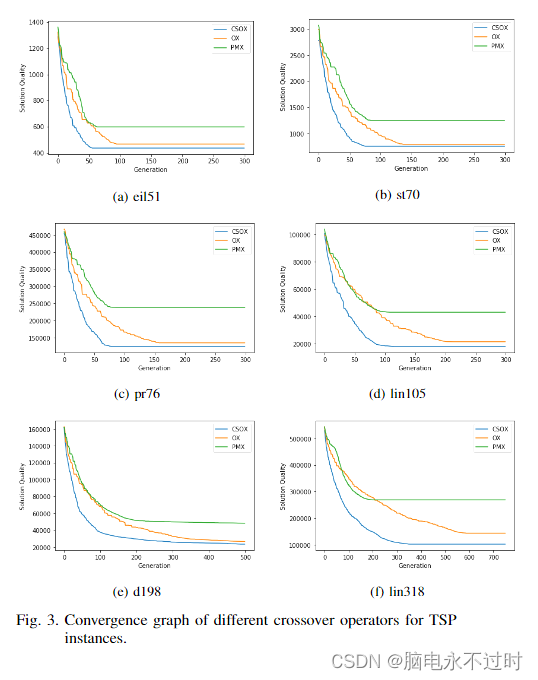
图3显示了解的收敛性,它对应于TSP实例的生成数量。同样,CSOX的收敛性能优于PMX和OX,包括解决方案质量。CSOX最多可产生六个后代,这对其他运营商来说是有利的,这是一种不公平的测试。因此,执行时间是该测试的度量标准。该实验定义了满足解决方案时的终止条件,以评估执行时间。
定义操作员遇到的终止条件,以评估执行时间。终止条件是三个运算符的最低平均解,即PMX。
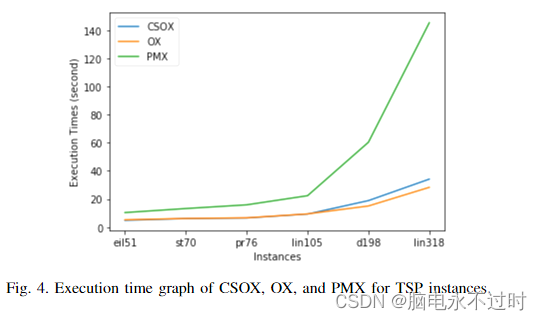
从图4中可以看出,对于eil51、st70、pr76和lin105,CSOX和OX的执行时间相似。相比之下,d198和lin318的OX执行时间更短。PMX在所有实例中具有最多的执行时间。
V.结论
CSOX是一种基于遗传算法的新阶交叉算子,用于求解TSP问题。就解决方案质量而言,CSOX可以比其他交叉运营商产生更好的结果。最重要的是,在任何实验中都没有使用突变算子。尽管CSOX最多能产生六个后代,但计算时间并不高。此外,CSOX在其他TSP实例中进行了测试,并在许多实例中表现良好
相关文章:

旅行推销员问题的遗传算法中的完整子路线顺序交叉
摘要 旅行商问题(TSP)是许多著名的组合问题之一。TSP可以解释为很难找到从第一个城市出发,经过所有城市,然后返回起点的最短距离。在标准问题中,TSP通常用于确定新算法的效率。遗传算法是求解TSP问题的一种成功算法。…...

Python实现词频统计
词频统计是自然语言处理的基本任务,针对一段句子、一篇文章或一组文章,统计文章中每个单词出现的次数,在此基础上发现文章的主题词、热词。 1. 单句的词频统计 思路:首先定义一个空字典my_dict,然后遍历文章…...
微信小程序面试题(day08)
文章目录微信小程序自定义组件的使用?微信小程序事件通道的使用?微信小程序如何使用vant组件库?微信小程序自定义组件父传子子传父?微信小程序自定义组件生命周期有哪些?微信小程序授权登录流程?web-view。…...
最强的Python可视化神器,你有用过么?
数据分析离不开数据可视化,我们最常用的就是Pandas,Matplotlib,Pyecharts当然还有Tableau,看到一篇文章介绍Plotly制图后我也跃跃欲试,查看了相关资料开始尝试用它制图。 1、Plotly Plotly是一款用来做数据分析和可视…...
Ubuntu使用vnc远程桌面【远程内网穿透】
文章目录1.前言2.两台互联电脑的设置2.1 Windows安装VNC2.2 Ubuntu安装VNC2.3.Ubuntu安装cpolar3.Cpolar设置3.1 Cpolar云端设置3.2.Cpolar本地设置4.公网访问测试5.结语1.前言 记得笔者刚刚开始接触电脑时,还是win95/98的时代,那时的电脑桌面刚迈入图形…...

【C++】map、set、multimap、multiset的介绍和使用
我讨厌世俗,也耐得住孤独。 文章目录一、键值对二、树形结构的关联式容器1.set1.1 set的介绍1.2 set的使用1.3 multiset的使用2.map2.1 map的介绍2.2 map的使用2.3 multimap的使用三、两道OJ题1.前K个高频单词(less<T>小于号是小的在左面升序&…...
)
css学习14(多媒体查询)
目录 多媒体查询 语法 示例代码 通用媒体查询 媒体功能参考列表 多媒体查询 CSS的媒体查询是一种CSS的技术,它可以根据不同的设备类型、屏幕尺寸、方向、分辨率等条件来应用不同的CSS样式,从而为不同的设备和屏幕提供最佳的浏览体验。这样ÿ…...
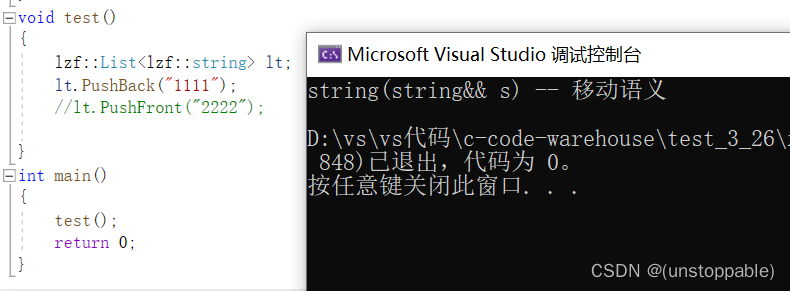
【C++进阶】C++11(中)左值引用和右值引用
文章目录左值引用左值引用的概念左值引用的使用右值引用右值引用的概念右值引用的使用左右值相互引用左值引用对右值进行引用右值引用对左值进行引用右值引用使用场景和意义左值引用的优势左值引用的短板右值引用的优势完美转发模板万能引用完美转发实际运用场景左值引用 左值…...

Python中的生成器【generator】总结,看看你掌握了没?
人生苦短,我用python python 安装包资料:点击此处跳转文末名片获取 1.实现generator的两种方式 python中的generator保存的是算法, 真正需要计算出值的时候才会去往下计算出值。 它是一种惰性计算(lazy evaluation)。 要创建一个…...
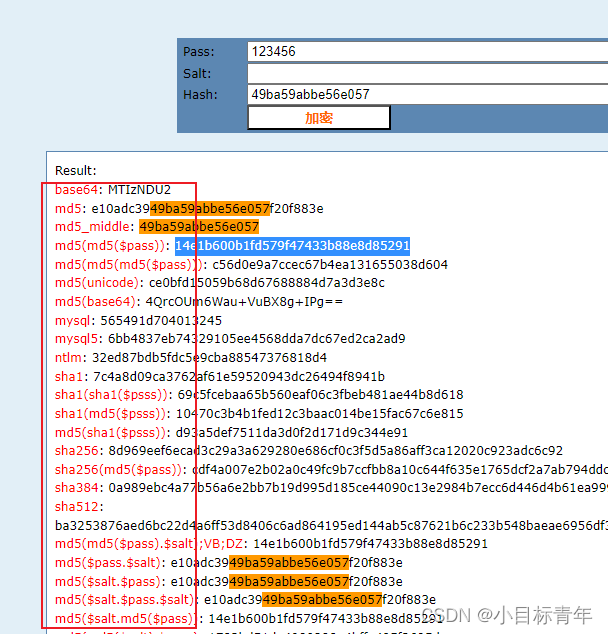
MD5加密竟然不安全,应届生表示无法理解?
前言 近日公司的一个应届生问我,他做的一个毕业设计密码是MD5加密存储的,为什么密码我帮他调试的时候,我能猜出来明文是什么? 第六感,是后端研发的第六感! 正文 示例,有个系统,前…...
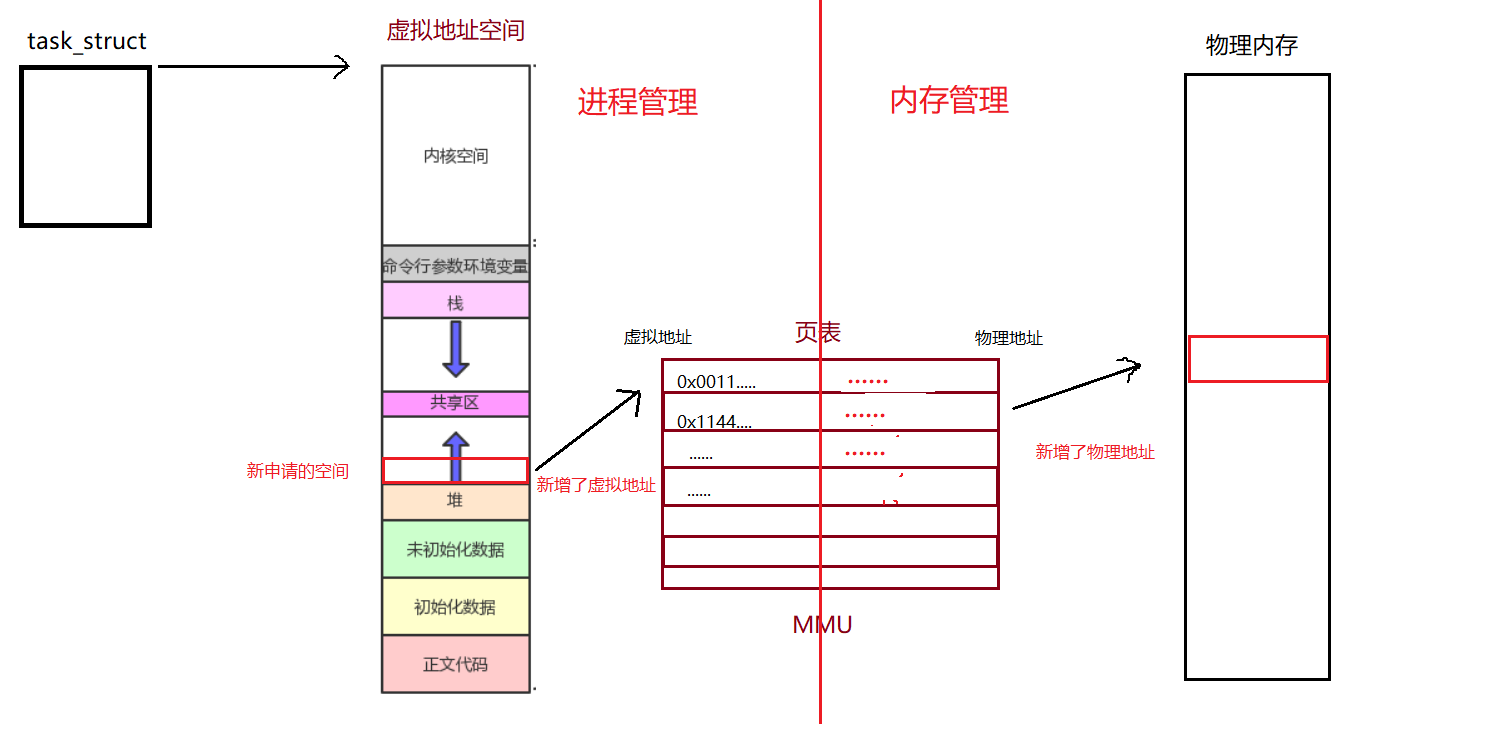
【Linux】虚拟地址空间
进程地址空间一、引入二、虚拟地址与物理内存的联系三、为什么要有虚拟地址空间一、引入 对于C/C程序,我们眼中的内存是这样的: 我们利用这种对于与内存的理解看一下下面这段代码: 运行结果: 观察父子进程中 val 变量的值&…...
四平方和题解(二分习题)
四平方和 暴力做法 Y总暴力做法,蓝桥云里能通过所有数据 总结:暴力也分好坏,下面这份代码就是写的好的暴力 如何写好暴力:1. 按组合枚举 2. 写好循环结束条件,没必要循环那么多次 #include<iostream> #include<cmath>…...

一篇文章搞定js正则表达式
我们测试正则表达式是否正确的方法有很多,例如通过正则表达式找到拼配的字符串: 在vscode编辑器中点击搜索框中的第三个按钮就可以实现: 或者 在浏览器中的控制台也可以实现: 我们可以通过下面的在线网站来测试你写的正则是否正确…...
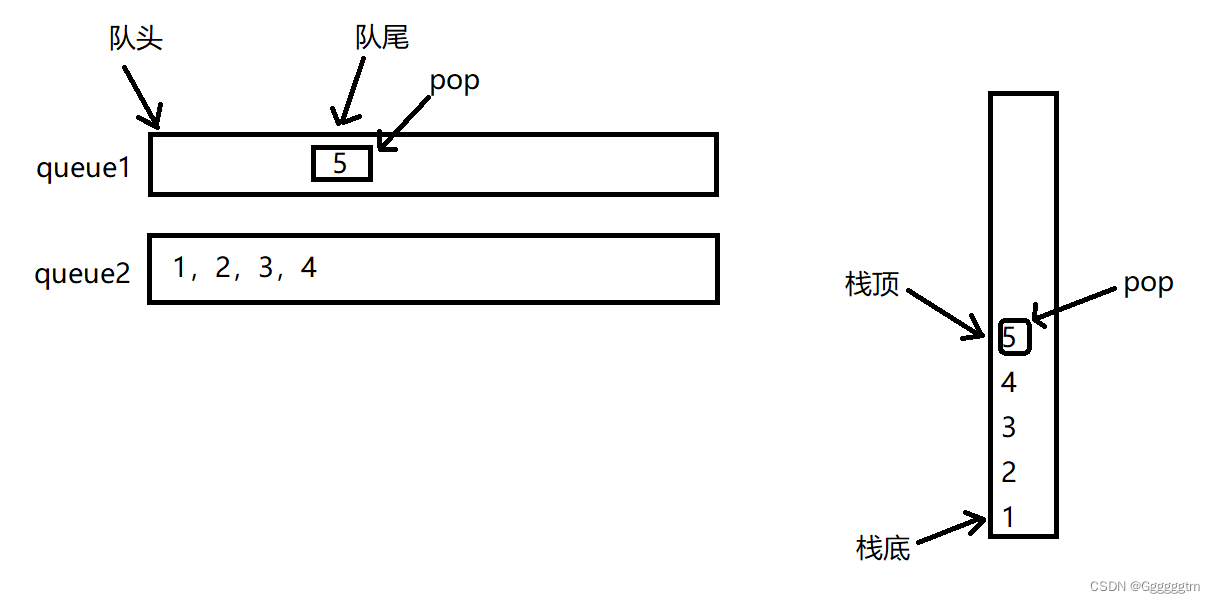
[数据结构] 用两个队列实现栈详解
文章目录 一、队列实现栈的特点分析 1、1 具体分析 1、2 整体概括 二、队列模拟实现栈代码的实现 2、1 手撕 队列 代码 queue.h queue.c 2、2 用队列模拟实现栈代码 三、总结 🙋♂️ 作者:Ggggggtm 🙋♂️ 👀 专栏࿱…...

官宣|Apache Flink 1.17 发布公告
Apache Flink PMC(项目管理委员)很高兴地宣布发布 Apache Flink 1.17.0。Apache Flink 是领先的流处理标准,流批统一的数据处理概念在越来越多的公司中得到认可。得益于我们出色的社区和优秀的贡献者,Apache Flink 在 Apache 社区…...
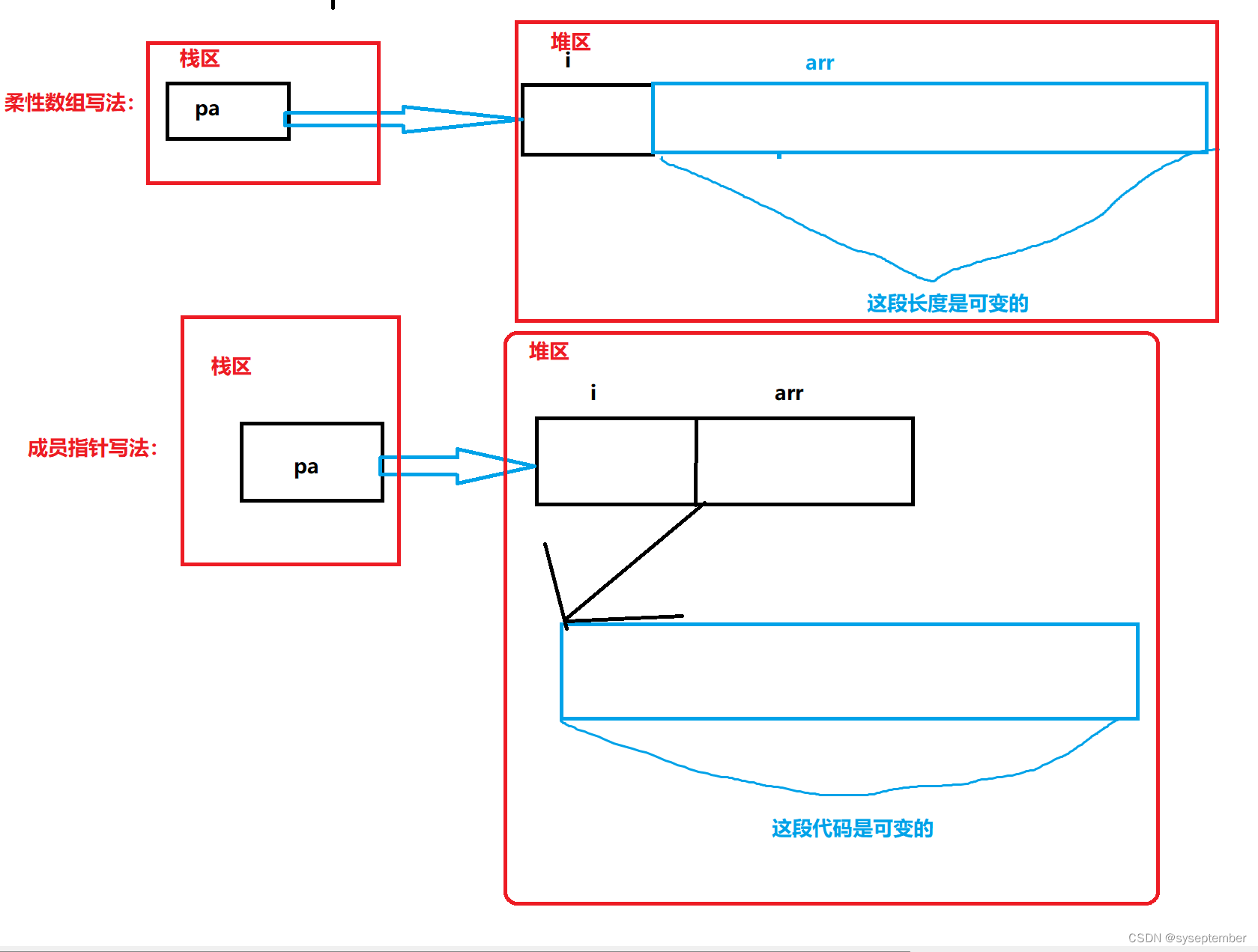
动态内存管理+动态通讯录【C进阶】
文章目录为什么存在动态内存分配❓👉动态内存函数👈malloc&freecallocrealloc❌常见的动态内存错误❌练习题🫠C/C程序的内存开辟🤔柔性数组柔性数组的特点柔性数组的优势:star:动态通讯录:star:初始化添加销毁为什么存在动态内…...
基于pytorch+Resnet101加GPT搭建AI玩王者荣耀
本源码模型主要用了SamLynnEvans Transformer 的源码的解码部分。以及pytorch自带的预训练模型"resnet101-5d3b4d8f.pth"本资源整理自网络,源地址:https://github.com/FengQuanLi/ResnetGPT注意运行本代码需要注意以下几点 注意!&a…...
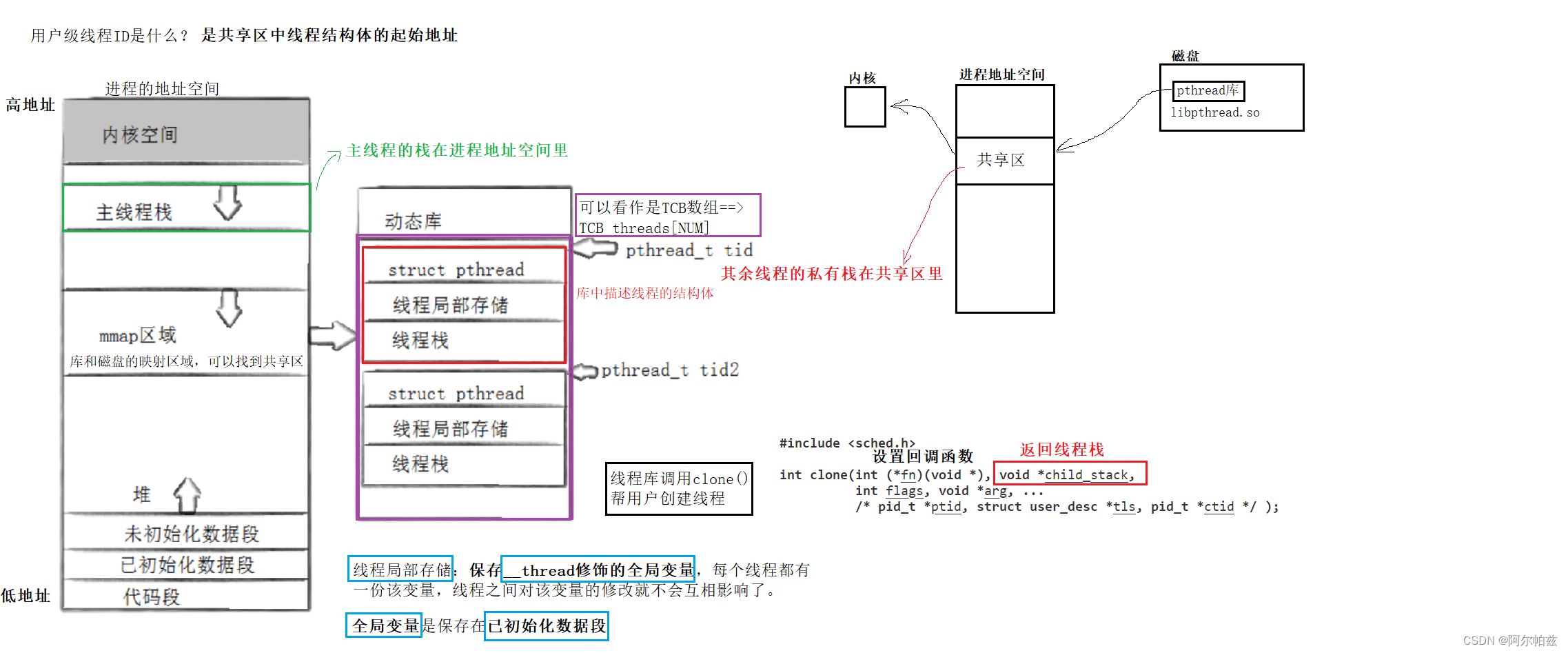
多线程控制讲解与代码实现
多线程控制 回顾一下线程的概念 线程是CPU调度的基本单位,进程是承担分配系统资源的基本单位。linux在设计上并没有给线程专门设计数据结构,而是直接复用PCB的数据结构。每个新线程(task_struct{}中有个指针都指向虚拟内存mm_struct结构&am…...
清晰概括:进程与线程间的区别的联系
相关阅读: 🔗通俗简介:操作系统之进程的管理与调度🔗如何使用 jconsole 查看Java进程中线程的详细信息? 目录 一、进程与线程 1、进程 2、线程 二、进程与线程之间的区别和联系 1、区别 2、联系 一、进程与线程 …...

自定义类型 (结构体)
文章目录📬结构体的声明🔎1.结构的基础知识🔎2.结构的声明🔎3.特殊的声明🔎4.结构的自引用🔎5.结构体变量的定义和初始化🔎6.结构体内存对齐🔎7.修改默认对齐数🔎8.结构体…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...

node.js的初步学习
那什么是node.js呢? 和JavaScript又是什么关系呢? node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说, 需要在node.js的环境上进行当JavaScript作为前端开发语言来说,需要在浏览器的环境上进行 Node.js 可…...

leetcode_69.x的平方根
题目如下 : 看到题 ,我们最原始的想法就是暴力解决: for(long long i 0;i<INT_MAX;i){if(i*ix){return i;}else if((i*i>x)&&((i-1)*(i-1)<x)){return i-1;}}我们直接开始遍历,我们是整数的平方根,所以我们分两…...
