浅谈虚树
问题引入
你是否遇到过下面这种问题:
SDOI2011 消耗战
在一场战争中,战场由 nnn 个岛屿和 n−1n-1n−1 个桥梁组成,保证每两个岛屿间有且仅有一条路径可达。现在,我军已经侦查到敌军的总部在编号为1的岛屿,而且他们已经没有足够多的能源维系战斗,我军胜利在望。已知在其他 kkk 个岛屿上有丰富能源,为了防止敌军获取能源,我军的任务是炸毁一些桥梁,使得敌军不能到达任何能源丰富的岛屿。由于不同桥梁的材质和结构不同,所以炸毁不同的桥梁有不同的代价,我军希望在满足目标的同时使得总代价最小。
侦查部门还发现,敌军有一台神秘机器。即使我军切断所有能源之后,他们也可以用那台机器。机器产生的效果不仅仅会修复所有我军炸毁的桥梁,而且会重新随机资源分布(但可以保证的是,资源不会分布到1号岛屿上)。不过侦查部门还发现了这台机器只能够使用m次,所以我们只需要把每次任务完成即可。
对于 100%100\%100% 的数据,2<=n<=250000,m>=1,∑ki<=500000,1<=ki<=n−12<=n<=250000,m>=1,\sum k_i<=500000,1<=k_i<=n-12<=n<=250000,m>=1,∑ki<=500000,1<=ki<=n−1
很明显,这是一道树形 DP 的题,但是如果我们对于每次任务都重新做一次树形DP,就会超时。
这时候我们想,我们每次重新树形 DP,有很多点是没有任何用的, 我们可以只将有用的点提出来,重新建棵树,在做树形 DP。
这就是虚树的基本思想。
思想
我们先来看看原树的 DP 如何实现:
fi={min(∑j∈sonifj,mindi)i不是资源点mindii是资源点f_i = \left \{ \begin{array}{ll} min(\sum_{j \in son_i} f_ j, mind_i) &i不是资源点\\ mind_i &i是资源点\\ \end{array} \right. fi={min(∑j∈sonifj,mindi)mindii不是资源点i是资源点
其中 fif_ifi 表示第 iii 个子树中所有资源点到根节点都断开的最小代价,mindimind_imindi 表示点 iii 到根节点的所有的边的最小值。
答案就是 f1f_1f1。
因为其中有很多节点删去,然后将它的儿子连向它的父亲之后并不会对答案产生任何影响。(在 mindimind_imindi 已经求出来的情况下)
所以我们可以将所有没用的节点删去,将有用的节点保留下来,连成一棵树,再在树上做 DP,此时的答案跟在原树的答案是一样的。
接下来,我们看看哪些节点是对我们有用的。
首先就是每一个资源点。(其实并不是所有的资源点,如果一个资源点的祖先有资源点,则该节点可不用考虑,因为如果删的边在该节点到祖先的资源点之间,则该资源点的祖先还要再删,所以可以不用考虑当前的节点)
然后就是资源点之间的 LCA。
为什么是资源点之间的 LCA 呢?
我们可以看回 DP 式。
fi={min(∑j∈sonifj,mindi)i不是资源点mindii是资源点f_i = \left \{ \begin{array}{ll} min(\sum_{j \in son_i} f_ j, mind_i) &i不是资源点\\ mind_i &i是资源点\\ \end{array} \right. fi={min(∑j∈sonifj,mindi)mindii不是资源点i是资源点
因为我们保证该子树没有可以到根节点的路径的话不是删除当前子树的根节点到父亲的边,而是当前子树的根节点到原树的根节点的所有边的最小值。
所以保存 LCA 一定不会比保存 LCA 的祖先更劣。
于是我们就可以将所有有用的点取出来,按照原本的祖先顺序连成一棵树,再在树上做 DP 就可以了。
实现
我们看看如何将所有有用的点拉出来重新建一棵树。
首先我们求出原树的 dfs 序。
然后我们用一个栈来存储,现将根节点入栈。
我们将所有的资源点按 dfs 序排序,从小到大入栈。
对于 iii 节点入栈,计 iii 节点跟栈顶的节点的 LCA 为 lcalcalca,我们分一下几种情况:
- 栈里面只有根节点,此时直接将该节点入栈就好了。
- 如果我的栈的顶是我的祖先,则直接跳过该节点。
- 如果 lcalcalca 的 dfs 序小于等于栈顶的下一个节点的 dfs 序,则将栈顶和栈顶的下一个节点连边,并且弹出栈顶。
- 做完 3 号操作后,判断 lcalcalca 跟栈顶是否相等,如果不相等,则用 lcalcalca 代替栈顶。
- 最后将该节点入栈。
对于所有节点做完之后,如果栈里面还有节点,则一一弹出,并将相邻两个节点连边。
单看是很难理解的, 最好画图模拟一下,可以加深理解。
可以参考下下面的代码。
void build(){tot=0;stk[++tot]=1;for(int i=1;i<=m;i++){if(tot==1)stk[++tot]=a[i];int lca=LCA(stk[tot],a[i]);if(lca==stk[tot])continue;while(dfn[lca]<=dfn[stk[tot - 1]] && tot>1)addedge(stk[tot - 1],stk[tot]),tot--;if(lca != stk[tot])addedge(lca,stk[tot]),stk[tot]=lca;stk[++tot]=a[i];}while(tot>1)addedge(stk[tot - 1],stk[tot]),tot--;
}
到这里,整个过程就完成了。
代码
下面是开头给出的题目的代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
namespace solve{int Ecnt,last[500005],m,dfn[500005],fa[500005][35],d[500005],a[500005];LL mind[500005];int stk[500005],tot;struct Edge { int to,next;} E[500005];bool cmp(int a,int b){ return dfn[a]<dfn[b];}void addedge(int u,int v){ Ecnt++,E[Ecnt].to=v,E[Ecnt].next=last[u],last[u]=Ecnt;}int LCA(int x,int y){if(d[x]<d[y])swap(x,y);for(int i=20;~i;i--)if(d[fa[x][i]]>=d[y])x=fa[x][i];if(x==y)return x;for(int i=20;~i;i--)if(fa[x][i] !=fa[y][i])x=fa[x][i],y=fa[y][i];return fa[x][0];}void build(){tot=0;stk[++tot]=1;for(int i=1;i<=m;i++){if(tot==1)stk[++tot]=a[i];int lca=LCA(stk[tot],a[i]);if(lca==stk[tot])continue;while(dfn[lca]<=dfn[stk[tot - 1]] && tot>1)addedge(stk[tot - 1],stk[tot]),tot--;if(lca != stk[tot])addedge(lca,stk[tot]),stk[tot]=lca;stk[++tot]=a[i];}while(tot>1)addedge(stk[tot - 1],stk[tot]),tot--;}LL dp(int x){if(last[x]==0)return mind[x];LL sum=0;for(int xy=last[x];xy;xy=E[xy].next)sum+=dp(E[xy].to);last[x]=0;return min(sum,mind[x]);}void main(){scanf("%d",&m);for(int i=1;i<=m;i++)scanf("%d",&a[i]);sort(a+1,a+1+m,cmp);build();printf("%lld\n",dp(1));Ecnt=0;}
}
int n,Q,Ecnt,cnt,last[500005];
struct Edge { int to,next;LL val;} E[500005];
void addedge(int u,int v,LL w){ Ecnt++,E[Ecnt].to=v,E[Ecnt].next=last[u],last[u]=Ecnt,E[Ecnt].val=w;}
void get_dfn(int x){solve::dfn[x]=++cnt;for(int xy=last[x];xy;xy=E[xy].next)if(E[xy].to !=solve::fa[x][0]){solve::mind[E[xy].to]=min(solve::mind[x],E[xy].val),solve::d[E[xy].to]=solve::d[x]+1;solve::fa[E[xy].to][0]=x;get_dfn(E[xy].to);}
}
void get_fa(){for(int i=1;i<=20;i++)for(int j=1;j<=n;j++)solve::fa[j][i]=solve::fa[solve::fa[j][i - 1]][i - 1];
}
int main(){scanf("%d",&n);for(int i=1;i<=n;i++)solve::mind[i]=1e16;LL w;for(int i=1,u,v;i<n;i++)scanf("%d%d%lld",&u,&v,&w),addedge(u,v,w),addedge(v,u,w);get_dfn(1);get_fa();scanf("%d",&Q);while(Q--)solve::main();return 0;
}
相关文章:

浅谈虚树
问题引入 你是否遇到过下面这种问题: SDOI2011 消耗战 在一场战争中,战场由 nnn 个岛屿和 n−1n-1n−1 个桥梁组成,保证每两个岛屿间有且仅有一条路径可达。现在,我军已经侦查到敌军的总部在编号为1的岛屿,而且他们已…...

裸机条件下写一个基于时间片轮转的多任务并发程序
目录前言A. 使用RTOSB.裸机多任务并发前言 在学习各种MCU的时候,都是用在main函数里写一个while(1){/* 执行代码 */},这种方式只能一个函数运行完以后再运行另一个函数。 假设需求控制多个模块,如显示屏幕信息的同时控制电机,还要…...

RK3588 系统定制开关机动画
平台:ITX-3588J, ROC-RK3588S-PC 系统:Android12.0 作者:jpchen & zzz 一. 功能描述 定制自己的开机动画和关机动画 二. 功能实现 1.开启功能 修改device/rockchip/common/BoardConfig.mk文件 BOOT_SHUTDOWN_ANIMATION_RINGINGtrue2.…...

水文-编程命令快查手册
前言 脑子里面记不住一些命令,每次遇到都得查下。我经常在三个实体电脑,windows/uos/ubuntu不同系统上编程。 所以web版本的笔记查看起来方便点。这里报错下。 二级标题 cmake windows在cmake --build的时候,使用–config,指定…...
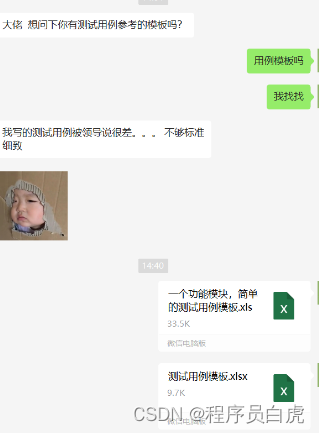
如何优雅编写测试用例
当你学会了如何设计测试用例之后,接下来便是开始用例的编写。 在设计阶段,更准确的说应该是识别测试点的过程,而编写阶段则是将测试点细化成一条条测试用例的过程,有了比较全的用例场景后,如何让别人更舒服、更方便、…...

[入门必看]数据结构2.3:线性表的链式表示
[入门必看]数据结构2.3:线性表的链式表示第二章 线性表2.3 线性表的链式表示知识总览2.3.1 单链表的定义2.3.2_1 单链表的插入删除2.3.2_2 单链表的查找2.3.2_3 单链表的建立2.3.3 双链表2.3.4 循环链表2.3.5 静态链表2.3.6 顺序表和链表的比较2.3.1 单链表的定义单…...
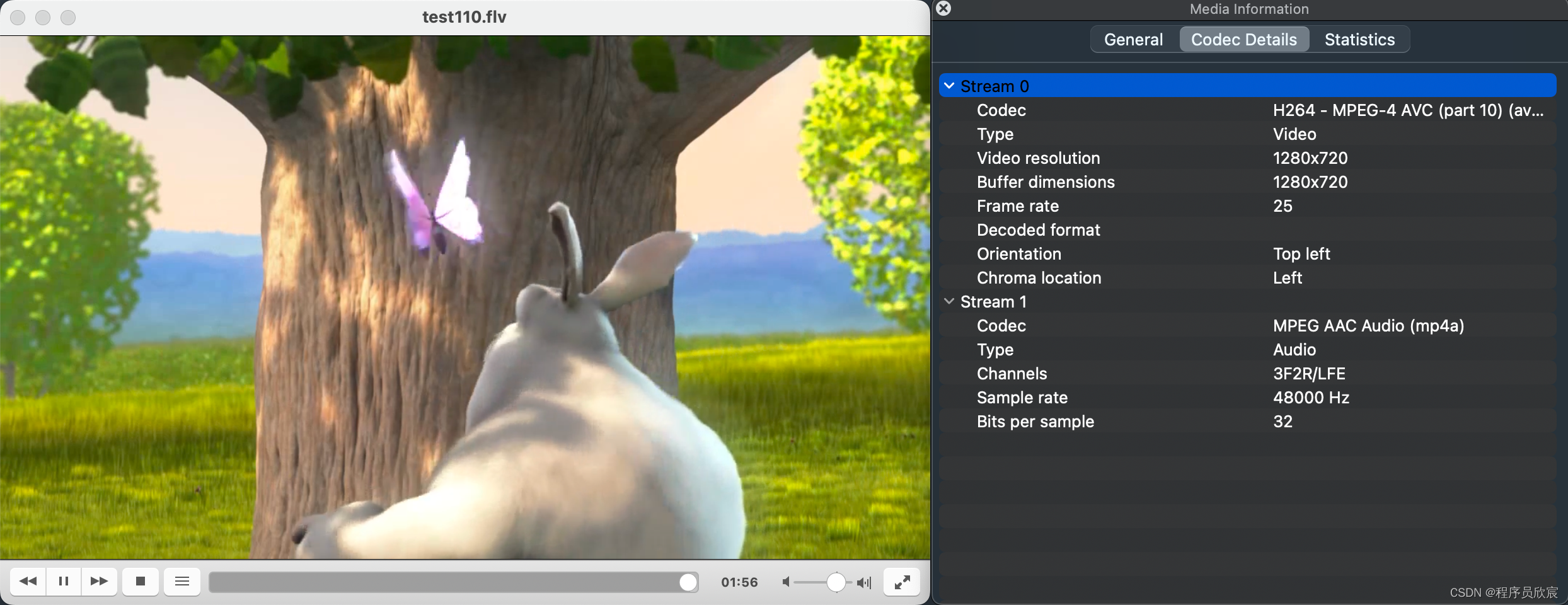
Golang流媒体实战之二:回源
欢迎访问我的GitHub 这里分类和汇总了欣宸的全部原创(含配套源码):https://github.com/zq2599/blog_demos 本篇概览 今天的实战是流传输过程中的常见功能:回源如下图,lal(源站)和lal(拉流节点)代表两台电脑,上面都部署了lalVLC在…...

webgl——给场景添加光
文章目录前言光照理论介绍光照效果光源类型反射光颜色向场景中添加光向场景中添加环境光和点光源逐片元光照——更加逼真总结前言 在之前的学习中已经将三维物体添加到了场景中,但是并没有在场景中使用光,照可以使模型更具有立体感,本文主要…...

Vue实战【Vue项目开发时常见的几个错误】
目录🌟前言🌟安装超时(install timeout)🌟can’t not find ‘xxModule’ - 找不到某些依赖或者模块🌟data functions should return an object🌟给组件内的原生控件添加事件,不生效了🌟我在函数内用了this.…...

【多线程】常见的锁策略
✨个人主页:bit me👇 ✨当前专栏:Java EE初阶👇 ✨每日一语:老当益壮,宁移白首之心;穷且益坚,不坠青云之志。 目 录🏳️一. 乐观锁 vs 悲观锁🏴二. 普通的互斥…...
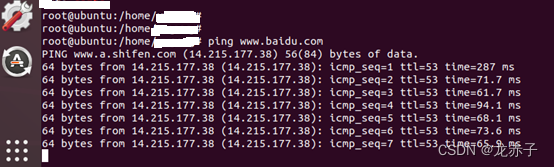
如何让虚拟机里的Ubuntu通过连接手机USB数据线上网
目录 一 前言 二 Windows联网方法 三 Ubuntu联网方法 一 前言 最近遇到了这样一个问题,有一台台式机,地插网口无法访问外网,周边也没有无线路由器,要访问外网,该如何做?进一步的,这台台式机…...
)
windows渗透(sam、system文件导出)
通过本地PC中渗透测试平台Kali对服务器场景Windows进行系统服务及版本扫描渗透测试,并将该操作显示结果中Telnet服务对应的端口号作为FLAG提交;通过本地PC中渗透测试平台Kali对服务器场景Windows进行系统服...
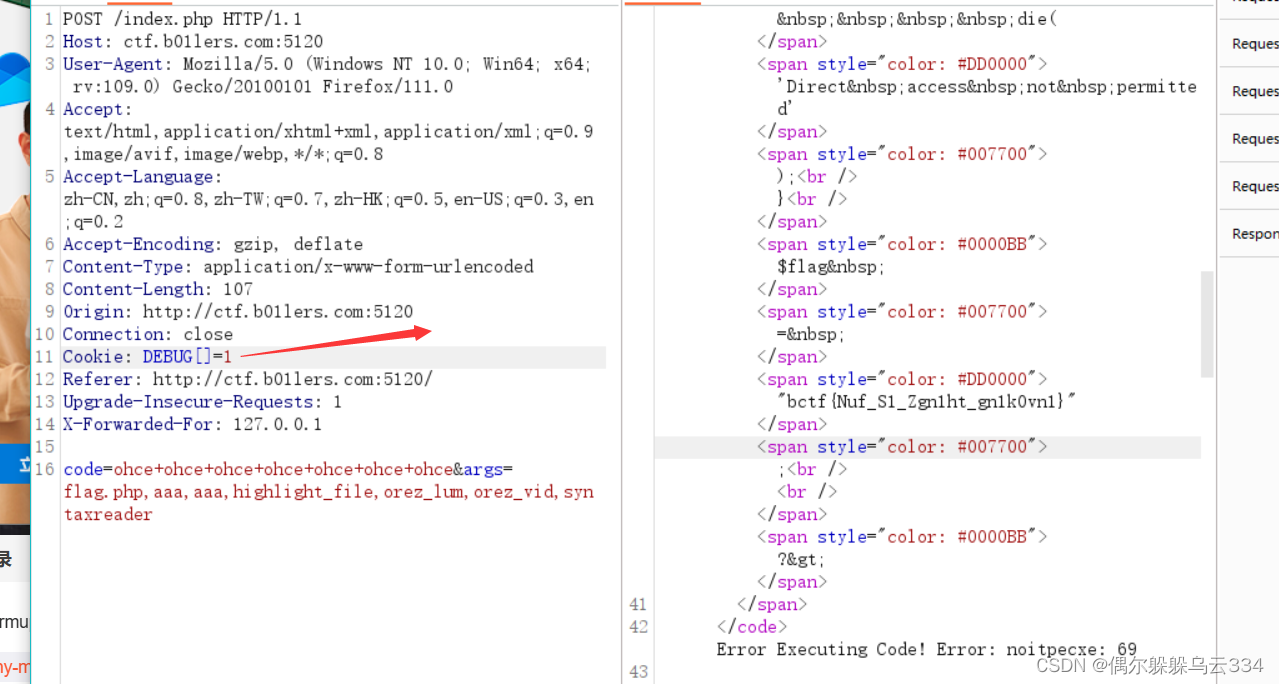
b01lers(php.galf)
目录 前文 正文 前文 <?phpclass A{public $codeNULL;public $argsNULL;public function __construct($code,$argsNULL){$this->code$code;$this->args$args;print_r("2333") ;} public function __invoke($code,$args){echo $code;print_r("执行inv…...
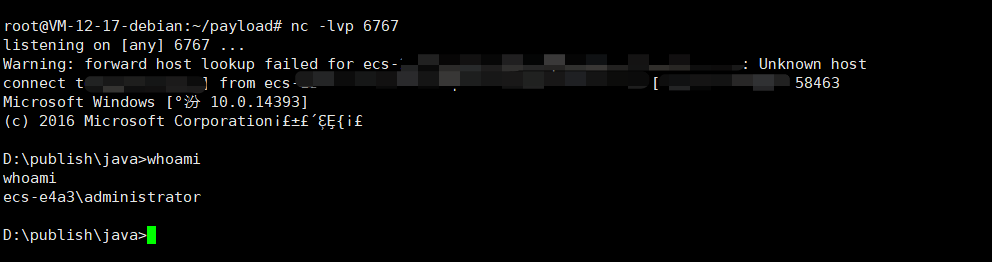
记一次若依后台管理系统渗透
前言 最近客户开始hw前的风险排查,让我们帮他做个渗透测试,只给一个单位名称。通过前期的信息收集,发现了这个站点: 没有验证码,再加上这个图标,吸引了我注意: 从弱口令开始 若依默认口令为ad…...
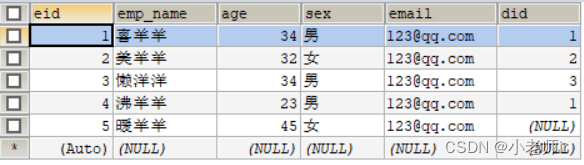
Mybatis(四):自定义映射resultMap
自定义映射resultMap前言一、处理字段和属性的映射关系问题:方案一:使用别名方案二:在mybatis-config.xml中设置mapUnderscoreToCamelCase方案三:在映射文件中设置redultMap二、多对一映射处理问题:方案一:…...
机器学习---降维算法
知其然知其所以然【写在前面】主成分分析(PCA)原理部分代码部分可视化部分线性判别分析(LDA)原理部分代码部分可视化部分独立成分分析(ICA)原理部分代码部分可视化部分t-SNE降维算法原理部分代码部分可视化…...

【Vue2从入门到精通】详解Vue.js的15种常用指令及其使用场景
文章目录前言1. v-text / {{ expression }}2.v-html3.v-bind4.v-on5. v-model6.v-for7.v-if / v-else-if / v-else9.v-show10.v-cloak11.v-pre12.组件注册指令13.动态组件指令14.自定义指令15.过滤器指令前言 Vue.js 是一款流行的前端框架,它通过指令(Di…...

数据库知识总结
数据库知识点总结个人向。 目录第一章 绪论第二章 关系数据库第三章 关系数据库标准语言SQL第四章 数据库安全性第五章 数据库完整性第六章 关系数据理论第七章 数据库设计第十章 数据库恢复技术第十一章 并发控制第一章 绪论 数据(data): 描述事物的符号记录。 数据库(DataB…...

处理数组循环中删除元素导致索引错位情况
就是很多时候我们对一个数组进行操作的时候,在for遍历的过程中删掉了一个元素,那么在删掉那个元素之后的所有元素的索引值都会减少一位,数组长度缩短一位,删完之后,正在进行的循环会继续循环下去,但是循环的…...
快速排序,分治法实际应用(含码源与解析)
🎊【数据结构与算法】专题正在持续更新中,各种数据结构的创建原理与运用✨,经典算法的解析✨都在这儿,欢迎大家前往订阅本专题,获取更多详细信息哦🎏🎏🎏 🪔本系列专栏 -…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
