机器学习---降维算法
知其然知其所以然
- 【写在前面】
- 主成分分析(PCA)
- 原理部分
- 代码部分
- 可视化部分
- 线性判别分析(LDA)
- 原理部分
- 代码部分
- 可视化部分
- 独立成分分析(ICA)
- 原理部分
- 代码部分
- 可视化部分
- t-SNE降维算法
- 原理部分
- 代码部分
- 可视化部分
【写在前面】
【以下使用的数据量很少很少,因此在散点图中展示不出具体算法特点,请读者自行实验。】
常用的降维算法有主成分分析(PCA)、线性判别分析(LDA)、独立成分分析(ICA)、t-SNE等。以下是这些算法的Python代码示例,分享一下我对降维的理解:
对一个样本矩阵,一是换特征,找一组新的特征来重新表示;二是减少特征,新特征的数目要远小于原特征的数目。这样一来就可以得到数量少且比较好的几个变量一构建模型。但是,降维也可能会导致信息的损失和模型的过拟合,因此需要谨慎使用。
- 创建数据
- 创建模型对象
- 拟合数据
- 转换数据
- 输出数据
主成分分析(PCA)
原理部分
- 通常把转化生成的综合指标称之为主成分
- 每个主成分都是原始变量的线性组合,且每个主成分之间互不相干
- 主成分分析(PCA)是一种常用的数据降维技术,它通过线性变换将高维数据转换为低维数据,同时保留原始数据的主要特征。PCA的基本思想是将原始数据映射到一个新的坐标系中,使得新坐标系下数据的方差最大化。这个新坐标系的轴称为主成分,每个主成分都是原始数据中的线性组合。PCA的应用广泛,例如在图像处理、信号处理、模式识别、数据挖掘等领域中都有广泛应用。在数据分析中,PCA可以用于降低数据的维度,减少数据冗余,提高数据处理效率,同时也可以帮助我们发现数据的内在结构和规律,从而更好地理解数据。
- 在实际应用中,PCA的步骤主要包括数据标准化、计算协方差矩阵、求解特征值和特征向量、选取主成分和投影数据等。通过PCA,我们可以得到一些重要的结果,例如主成分的贡献率、主成分的方差解释比例、主成分的系数等。这些结果可以帮助我们更好地理解数据的结构和特征,从而为后续的数据分析和建模提供更好的基础。
代码部分
from sklearn.decomposition import PCA
import numpy as np# 创建数据
X = np.array([[1, 2, 3, 6, 10, 22, 3, 2, 3], [4, 5, 6, 8, 9, 23, 5, 2, 6], [7, 8, 9, 10, 2, 24, 9, 9, 5]])# 创建PCA对象
pca = PCA(n_components=2)# 拟合数据
pca.fit(X)# 转换数据
X_new = pca.transform(X)print(X_new)

可视化部分

线性判别分析(LDA)
原理部分
线性判别分析(Linear Discriminant Analysis,简称LDA)是一种经典的监督学习算法,它既可以作为分类器,也可以作为降维技术。LDA的主要思想是将数据投影到一个低维空间中,使得不同类别之间的距离最大化,同一类别内部的距离最小化。这样可以在保留尽量多的信息的同时,将数据进行有效的分类。LDA的主要步骤包括:
- 计算每个类别的均值向量和整个数据集的均值向量。
- 计算类内散度矩阵(within-class scatter matrix)和类间散度矩阵(between-class scatter matrix)。
- 计算投影矩阵,将数据投影到低维空间中。
- 使用投影矩阵将数据进行降维或分类。
LDA的优点包括:
- 在保留尽量多信息的同时,可以将数据进行有效分类。
- 可以用于降维,减少数据维度,便于可视化和处理。
- 适用于高维数据集。
LDA的缺点包括:
- 对于非线性可分的数据集,LDA的效果会受到影响。
- 对于不平衡的数据集,可能会导致分类结果出现偏差。
- 在计算类内散度矩阵时,需要计算每个类别的协方差矩阵,如果数据维度很高,计算量会很大。
代码部分
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
import numpy as np# 创建数据
X = np.array([[1, 2, 3, 6, 10, 22, 3, 2, 3], [4, 5, 6, 8, 9, 23, 5, 2, 6], [7, 8, 9, 10, 2, 24, 9, 9, 5]])
y = np.array([0, 1, 0])# 创建LDA对象
lda = LinearDiscriminantAnalysis(n_components=1)# 拟合数据
lda.fit(X, y)# 转换数据
X_new = lda.transform(X)print(X_new)

可视化部分

独立成分分析(ICA)
原理部分
- 在机器学习中,ICA被广泛应用于信号处理、图像处理、语音识别等领域。
- ICA的基本思想是:假设存在一组独立的成分,它们通过线性组合形成了观测信号。通过对观测信号进行分解,可以得到独立的成分。
- ICA的目标是找到一组线性变换,使得变换后的信号成分之间相互独立。
- ICA的应用场景包括:语音信号分离、图像分离、生物信号分析等。例如,ICA可以用于将多个人说话的混合语音信号分离成单独的语音信号,或者将一张复杂的图像分解为不同的成分。
代码部分
from sklearn.decomposition import FastICA
import numpy as np# 创建数据
X = np.array([[1, 2, 3, 6, 10, 22, 3, 2, 3], [4, 5, 6, 8, 9, 23, 5, 2, 6], [7, 8, 9, 10, 2, 24, 9, 9, 5]])# 创建ICA对象
ica = FastICA(n_components=2)# 拟合数据
ica.fit(X)# 转换数据
X_new = ica.transform(X)print(X_new)

可视化部分

t-SNE降维算法
原理部分
- TSNE(t-Distributed Stochastic Neighbor
Embedding)是一种非线性降维算法,用于将高维数据降至二维或三维,以便于可视化。 - 该算法的基本思想是,将高维数据映射到低维空间中,使得在原始空间中相似的数据点在低维空间中也保持相似,而不相似的数据点在低维空间中则距离较远。
- TSNE算法主要分为两个步骤:首先,通过高斯核函数计算每个数据点与其它数据点之间的相似度,然后将这些相似度转化为概率分布。接着,在低维空间中,通过KL散度最小化的方法,将这些概率分布转化为新的低维空间中的概率分布。最终,通过梯度下降算法,将低维空间中的数据点的位置不断调整,使得其与高维空间中的数据点的相似度尽可能地保持一致。
- TSNE算法的优点是能够在保持数据点之间的相对距离的同时,有效地将高维数据映射到低维空间中,从而便于可视化和分析。但是,该算法的计算复杂度较高,需要较长的计算时间和计算资源。
代码部分
from sklearn.manifold import TSNE
import numpy as np# 创建数据
X = np.array([[1, 2, 3, 6, 10, 22, 3, 2, 3], [4, 5, 6, 8, 9, 23, 5, 2, 6], [7, 8, 9, 10, 2, 24, 9, 9, 5]])# 创建t-SNE对象
tsne = TSNE(n_components=2)# 转换数据
X_new = tsne.fit_transform(X)print(X_new)

可视化部分
相关文章:

机器学习---降维算法
知其然知其所以然【写在前面】主成分分析(PCA)原理部分代码部分可视化部分线性判别分析(LDA)原理部分代码部分可视化部分独立成分分析(ICA)原理部分代码部分可视化部分t-SNE降维算法原理部分代码部分可视化…...

【Vue2从入门到精通】详解Vue.js的15种常用指令及其使用场景
文章目录前言1. v-text / {{ expression }}2.v-html3.v-bind4.v-on5. v-model6.v-for7.v-if / v-else-if / v-else9.v-show10.v-cloak11.v-pre12.组件注册指令13.动态组件指令14.自定义指令15.过滤器指令前言 Vue.js 是一款流行的前端框架,它通过指令(Di…...

数据库知识总结
数据库知识点总结个人向。 目录第一章 绪论第二章 关系数据库第三章 关系数据库标准语言SQL第四章 数据库安全性第五章 数据库完整性第六章 关系数据理论第七章 数据库设计第十章 数据库恢复技术第十一章 并发控制第一章 绪论 数据(data): 描述事物的符号记录。 数据库(DataB…...

处理数组循环中删除元素导致索引错位情况
就是很多时候我们对一个数组进行操作的时候,在for遍历的过程中删掉了一个元素,那么在删掉那个元素之后的所有元素的索引值都会减少一位,数组长度缩短一位,删完之后,正在进行的循环会继续循环下去,但是循环的…...
快速排序,分治法实际应用(含码源与解析)
🎊【数据结构与算法】专题正在持续更新中,各种数据结构的创建原理与运用✨,经典算法的解析✨都在这儿,欢迎大家前往订阅本专题,获取更多详细信息哦🎏🎏🎏 🪔本系列专栏 -…...
linux入门---操作体统的概念
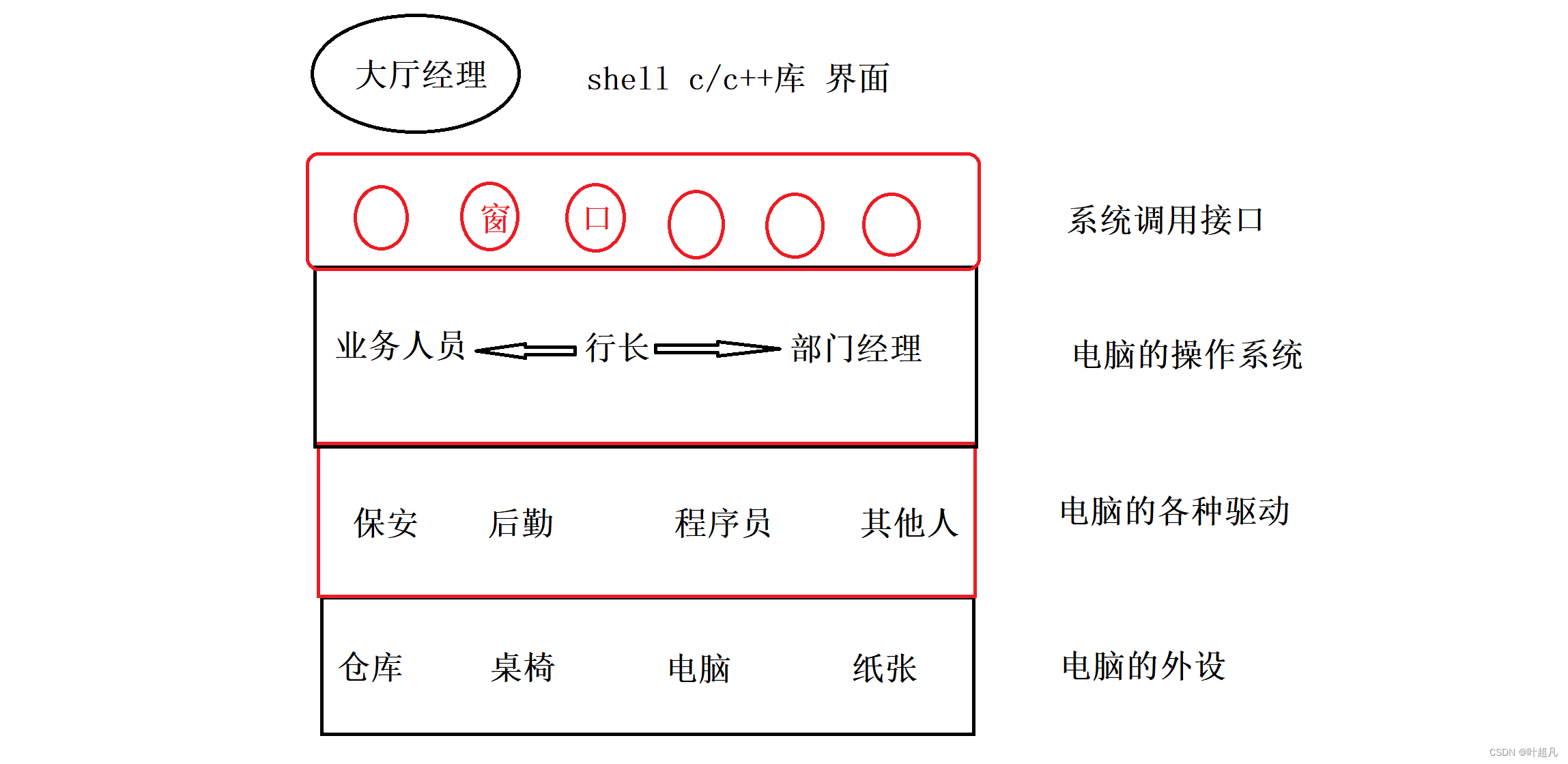
什么是操作系统 操作系统是一个对软硬件资源进行管理的软件。计算机由一堆硬件组成,这些硬件遵循着冯诺依曼体系结构 在这个硬件的基础上还有一个软件叫做操作系统 操作系统的任务是对硬件进行管理,既然是管理的话操作系统得访问到底层的硬件…...
《Qt 6 C++开发指南》提供4个版本的示例程序
《Qt 6 C开发指南》包含丰富的示例项目,为了方便读者使用《Qt 6 C开发指南》学习Qt编程,本书提供了4个版本的示例程序。读者可在人民邮电出版社异步社区本书的配套资源(如图1)里下载这4个版本的示例程序。图1 异步社区本书配套资源…...

chartgpt 告诉我的,loss 函数的各种知识
一、libtorch中常见的损失函数及其使用场景的总结1. CrossEntropyLoss:CrossEntropyLoss(交叉熵损失)主要用于分类任务。它适用于多分类问题,其中每个样本只属于一个类别(互斥)。该损失函数将预测概率与真实标签的one-…...
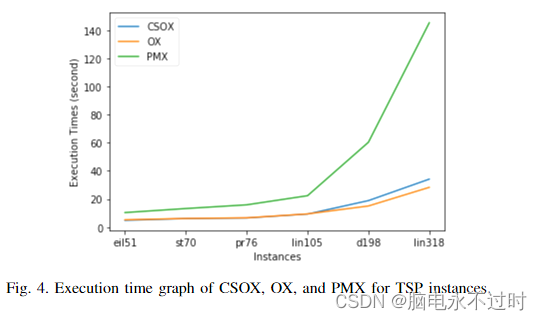
旅行推销员问题的遗传算法中的完整子路线顺序交叉
摘要 旅行商问题(TSP)是许多著名的组合问题之一。TSP可以解释为很难找到从第一个城市出发,经过所有城市,然后返回起点的最短距离。在标准问题中,TSP通常用于确定新算法的效率。遗传算法是求解TSP问题的一种成功算法。…...

Python实现词频统计
词频统计是自然语言处理的基本任务,针对一段句子、一篇文章或一组文章,统计文章中每个单词出现的次数,在此基础上发现文章的主题词、热词。 1. 单句的词频统计 思路:首先定义一个空字典my_dict,然后遍历文章…...
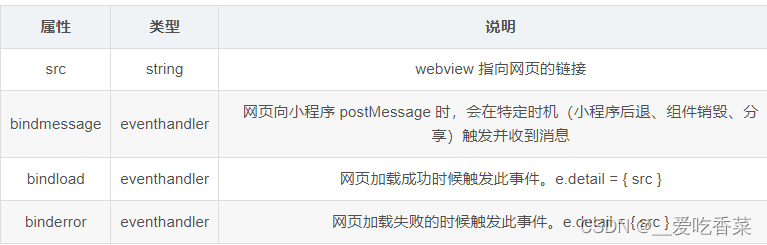
微信小程序面试题(day08)
文章目录微信小程序自定义组件的使用?微信小程序事件通道的使用?微信小程序如何使用vant组件库?微信小程序自定义组件父传子子传父?微信小程序自定义组件生命周期有哪些?微信小程序授权登录流程?web-view。…...
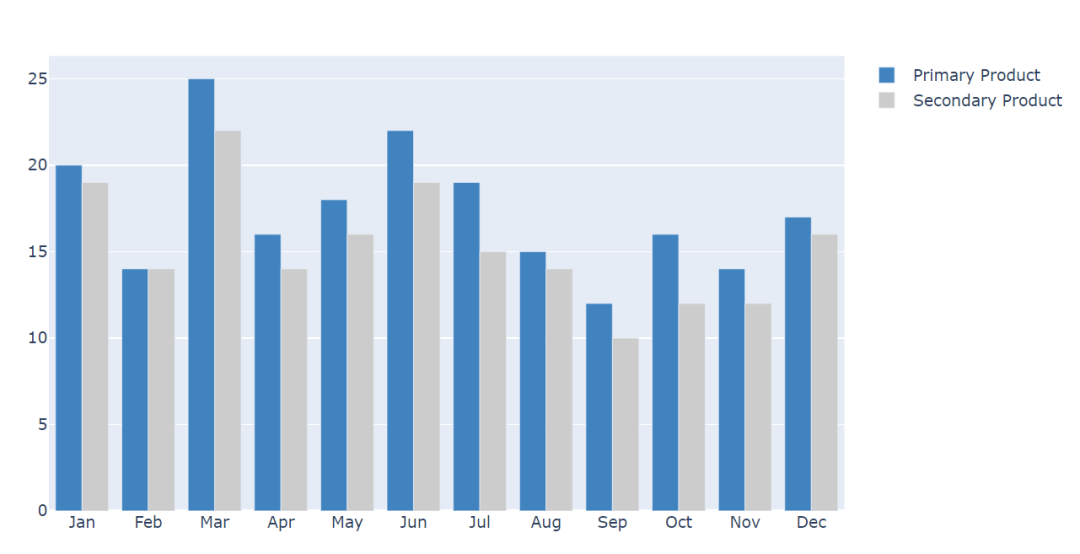
最强的Python可视化神器,你有用过么?
数据分析离不开数据可视化,我们最常用的就是Pandas,Matplotlib,Pyecharts当然还有Tableau,看到一篇文章介绍Plotly制图后我也跃跃欲试,查看了相关资料开始尝试用它制图。 1、Plotly Plotly是一款用来做数据分析和可视…...
Ubuntu使用vnc远程桌面【远程内网穿透】
文章目录1.前言2.两台互联电脑的设置2.1 Windows安装VNC2.2 Ubuntu安装VNC2.3.Ubuntu安装cpolar3.Cpolar设置3.1 Cpolar云端设置3.2.Cpolar本地设置4.公网访问测试5.结语1.前言 记得笔者刚刚开始接触电脑时,还是win95/98的时代,那时的电脑桌面刚迈入图形…...

【C++】map、set、multimap、multiset的介绍和使用
我讨厌世俗,也耐得住孤独。 文章目录一、键值对二、树形结构的关联式容器1.set1.1 set的介绍1.2 set的使用1.3 multiset的使用2.map2.1 map的介绍2.2 map的使用2.3 multimap的使用三、两道OJ题1.前K个高频单词(less<T>小于号是小的在左面升序&…...
)
css学习14(多媒体查询)
目录 多媒体查询 语法 示例代码 通用媒体查询 媒体功能参考列表 多媒体查询 CSS的媒体查询是一种CSS的技术,它可以根据不同的设备类型、屏幕尺寸、方向、分辨率等条件来应用不同的CSS样式,从而为不同的设备和屏幕提供最佳的浏览体验。这样ÿ…...
【C++进阶】C++11(中)左值引用和右值引用
文章目录左值引用左值引用的概念左值引用的使用右值引用右值引用的概念右值引用的使用左右值相互引用左值引用对右值进行引用右值引用对左值进行引用右值引用使用场景和意义左值引用的优势左值引用的短板右值引用的优势完美转发模板万能引用完美转发实际运用场景左值引用 左值…...

Python中的生成器【generator】总结,看看你掌握了没?
人生苦短,我用python python 安装包资料:点击此处跳转文末名片获取 1.实现generator的两种方式 python中的generator保存的是算法, 真正需要计算出值的时候才会去往下计算出值。 它是一种惰性计算(lazy evaluation)。 要创建一个…...
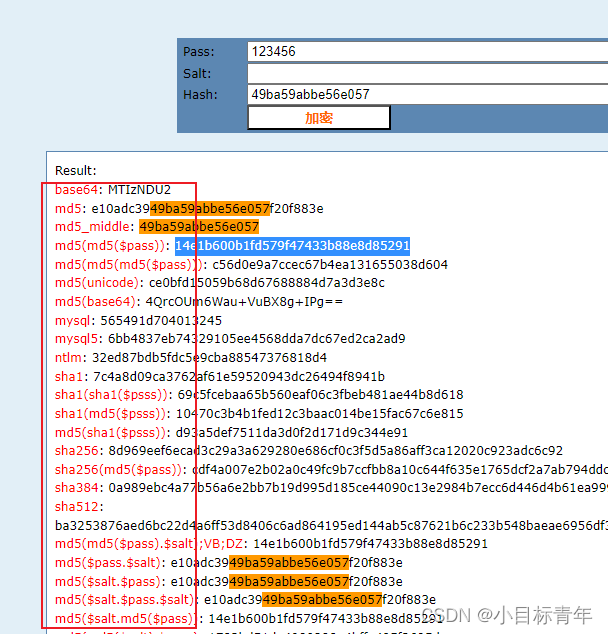
MD5加密竟然不安全,应届生表示无法理解?
前言 近日公司的一个应届生问我,他做的一个毕业设计密码是MD5加密存储的,为什么密码我帮他调试的时候,我能猜出来明文是什么? 第六感,是后端研发的第六感! 正文 示例,有个系统,前…...
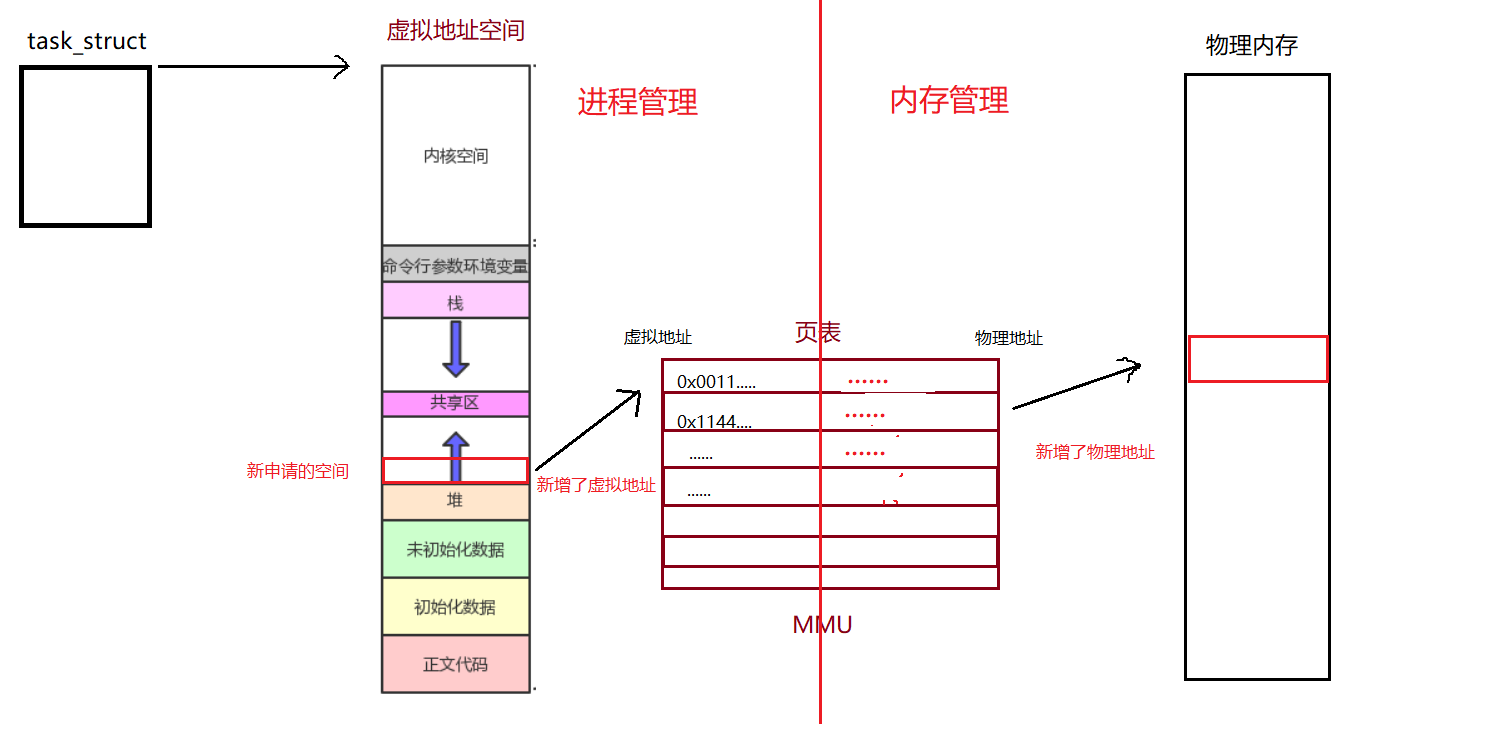
【Linux】虚拟地址空间
进程地址空间一、引入二、虚拟地址与物理内存的联系三、为什么要有虚拟地址空间一、引入 对于C/C程序,我们眼中的内存是这样的: 我们利用这种对于与内存的理解看一下下面这段代码: 运行结果: 观察父子进程中 val 变量的值&…...
四平方和题解(二分习题)
四平方和 暴力做法 Y总暴力做法,蓝桥云里能通过所有数据 总结:暴力也分好坏,下面这份代码就是写的好的暴力 如何写好暴力:1. 按组合枚举 2. 写好循环结束条件,没必要循环那么多次 #include<iostream> #include<cmath>…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

游戏开发中常见的战斗数值英文缩写对照表
游戏开发中常见的战斗数值英文缩写对照表 基础属性(Basic Attributes) 缩写英文全称中文释义常见使用场景HPHit Points / Health Points生命值角色生存状态MPMana Points / Magic Points魔法值技能释放资源SPStamina Points体力值动作消耗资源APAction…...

深入理解 React 样式方案
React 的样式方案较多,在应用开发初期,开发者需要根据项目业务具体情况选择对应样式方案。React 样式方案主要有: 1. 内联样式 2. module css 3. css in js 4. tailwind css 这些方案中,均有各自的优势和缺点。 1. 方案优劣势 1. 内联样式: 简单直观,适合动态样式和…...

Easy Excel
Easy Excel 一、依赖引入二、基本使用1. 定义实体类(导入/导出共用)2. 写 Excel3. 读 Excel 三、常用注解说明(完整列表)四、进阶:自定义转换器(Converter) 其它自定义转换器没生效 Easy Excel在…...
