快速排序,分治法实际应用(含码源与解析)

🎊【数据结构与算法】专题正在持续更新中,各种数据结构的创建原理与运用✨,经典算法的解析✨都在这儿,欢迎大家前往订阅本专题,获取更多详细信息哦🎏🎏🎏
🪔本系列专栏 - 数据结构与算法_勾栏听曲_0
🍻欢迎大家 🏹 点赞👍 评论📨 收藏⭐️
📌个人主页 - 勾栏听曲_0的博客📝
🔑希望本文能对你有所帮助,如有不足请指正,共同进步吧🏆
🎇莫将画竹论难易,刚道繁难简更难。君看萧萧只数叶,满堂春风不胜寒。📈
定义
快速排序是另一种基于分治技术的重要排序算法。与我们上一篇所讲的合并排序不一样。合并排序是按照元素在数组中的位置对它们进行划分,快速排序按照元素的值对它们进行划分。划分是对给定数组中的元素的重新排列,使得一个数组A[i],有s下标,A[s]左边的元素都小于等于A[s],而所有A[s]右边的元素都大于等于A[s]。
A[0]...A[s-1],A[s],A[s+1]...A[i-1]
显然,在对数组建立了一个划分以后,A[s]已经位于它在有序数组中的最终位置,接下来我们可以继续对A[s]前和A[s]后的子数组分别进行排序(例如,使用同样的方法)。注意,它与合并排序的不同之处在于:在合并排序算法中,将问题划分成两个子问题是很快的,算法的主要工作在于合并子问题的解;而在快速排序中,算法的主要工作在于划分阶段,而不需要再去合并子问题的解了。
伪代码
伪代码实现
Quicksort(A[ l..r ])
//用Quicksort对子数组排序
//输入:数组A[0..n-1]中的子数组A[ l..r ],由左右下标 l 和 r 定义//输出:非降序排列的子数组A[ l..r ]
if l < r
s <-Partition (A[1..r])//s是分裂位置Quicksort( A[ l.. (s - 1)])
Quicksort(A[(s +1)..r ])
算法解析
对于快速排序,有数组A[0..n-1],子数组A[e..r],我们要选择一个中轴,接下来会根据该元素的值来划分子数组。选择中轴有许多不同的策略,当我们分析该算法的效率时,我们会回到这个话题。现在,我们只使用最简单的策略——选择子数组的第一个元素,即p=A[0]。
然后 我们将分别从子数组的两端进行扫描,并且将扫描到的元素与中轴相比较。从左到右的扫描(下面用指针i表示)从第二个元素开始。因为我们希望小于中轴的元素位于子数组的左半部分,扫描会忽略小于中轴的元素,直到遇到第一个大于等于中轴的元素才会停止。从右到左的扫描(下面用指针j表示)从最后一个元素开始。因为我们希望大于中轴的元素位于子数组的右半部分,扫描会忽略大于中轴的元素,直到遇到第一个小于等于中轴的元素才会停止。(为什么当遇到与中轴元素相等的元素时值得停止扫描?因为当遇到有很多相同元素的数组时,这个方法可以将数组分得更加平均,从而使算法运行得更快。如果我们遇到相等元素时继续扫描,对于一个具有n个相同元素的数组来说,划分后得到的两个子数组的长度可能分别是n~1和0,从而在扫描了整个数组后只将问题的规模减1。)
两次扫描全部停止以后,取决于扫描的指针是否相交,会发生3种不同的情况。1、如果扫描指针i和 j不相交,也就是说i<j,我们简单地交换A[i]和A[j],再分别对i加1,对j减1,然后继续开始扫描;2、如果扫描指针相交,也就是说i> j,把中轴和A[j]交换以后,我们得到了该数组的一个划分;3、最后,如果扫描指针停下来时指向的是同一个元素,也就是说i= j,被指向元素的值一定等于p。(为什么?)因此,我们建立了该数组的一个划分,分裂点的位置s =i= j。
我们可以把第三种情况和指针相交的情况(i> j )结合起来,只要i≥j,就交换中轴和A[j]的位置。
下面我们来看看快速排序的视频案例
分治法_快速排序
时间效率分析
在开始讨论快速排序的效率以前,我们应该要注意;如果扫描指针交叉了,建立划分之前所执行的键值比较次数是n+1;如果它们相等,则是n。如果所有的分裂点位于相应子数组的中点,这就是最优的情况。在最优情况下,键值比较的次数Cbes(n)满足下面的递推式:
当n>1时,
根据主定理,;对于n=2*的情况求得
。
在最差的情况下,所有的分裂点都趋于极端:两个子数组有一个为空,而另一个子数组仅仅比被划分的数组少一个元素。具体来说,这种令人遗憾的情况会发生在升序的数组上,也就是说,输入的数组已经被排过序了!的确,如果 A[0..n –1]是严格递增的数组,并且我们将A[0]作为中轴,从左到右的扫描会停在A[1]上,而从右到左的扫描会一直处理到A[0]为止,导致分裂点出现在0这个位置。
所以,在进行了n+1次比较之后建立了划分,并且将A[0]和它本身进行了交换以后,快速排序算法还会对严格递增的数组A[1..n-1]进行排序。对规模减小了的严格递增数组的排序会一直继续到最后一个子数组A[n-2..n-1]。这种情况下,键值比较的总次数应该等于:
源码
#include <stdio.h>// 交换两个元素的值
void swap(int *a, int *b) {int temp = *a;*a = *b;*b = temp;
}// 分区函数
int partition(int arr[], int low, int high) {// 选取最后一个元素作为基准值int pivot = arr[high];// i指向小于基准值的最后一个元素int i = (low - 1);// 遍历数组,将小于基准值的元素放到左边,大于基准值的元素放到右边for (int j = low; j <= high - 1; j++) {if (arr[j] < pivot) {i++;swap(&arr[i], &arr[j]);}}// 将基准值放到中间swap(&arr[i + 1], &arr[high]);return (i + 1);
}// 快速排序函数
void quickSort(int arr[], int low, int high) {if (low < high) {// 将数组分为两部分,左边的元素都小于右边的元素int pi = partition(arr, low, high);// 递归排序左边的部分quickSort(arr, low, pi - 1);// 递归排序右边的部分quickSort(arr, pi + 1, high);}
}int main() {int arr[] = {10, 7, 8, 9, 1, 5};int n = sizeof(arr) / sizeof(arr[0]);quickSort(arr, 0, n - 1);printf("Sorted array: ");for (int i = 0; i < n; i++) {printf("%d ", arr[i]);}return 0;
}
如有小伙伴需要理解分治法思想或者合并排序,可阅读这篇文章哦
分治法实现合并排序(归并排序),理解分治算法思想,实现分治算法的完美例子合并排序(含码源与解析)
https://blog.csdn.net/weixin_53050357/article/details/129718346?spm=1001.2014.3001.5501
相关文章:
快速排序,分治法实际应用(含码源与解析)
🎊【数据结构与算法】专题正在持续更新中,各种数据结构的创建原理与运用✨,经典算法的解析✨都在这儿,欢迎大家前往订阅本专题,获取更多详细信息哦🎏🎏🎏 🪔本系列专栏 -…...
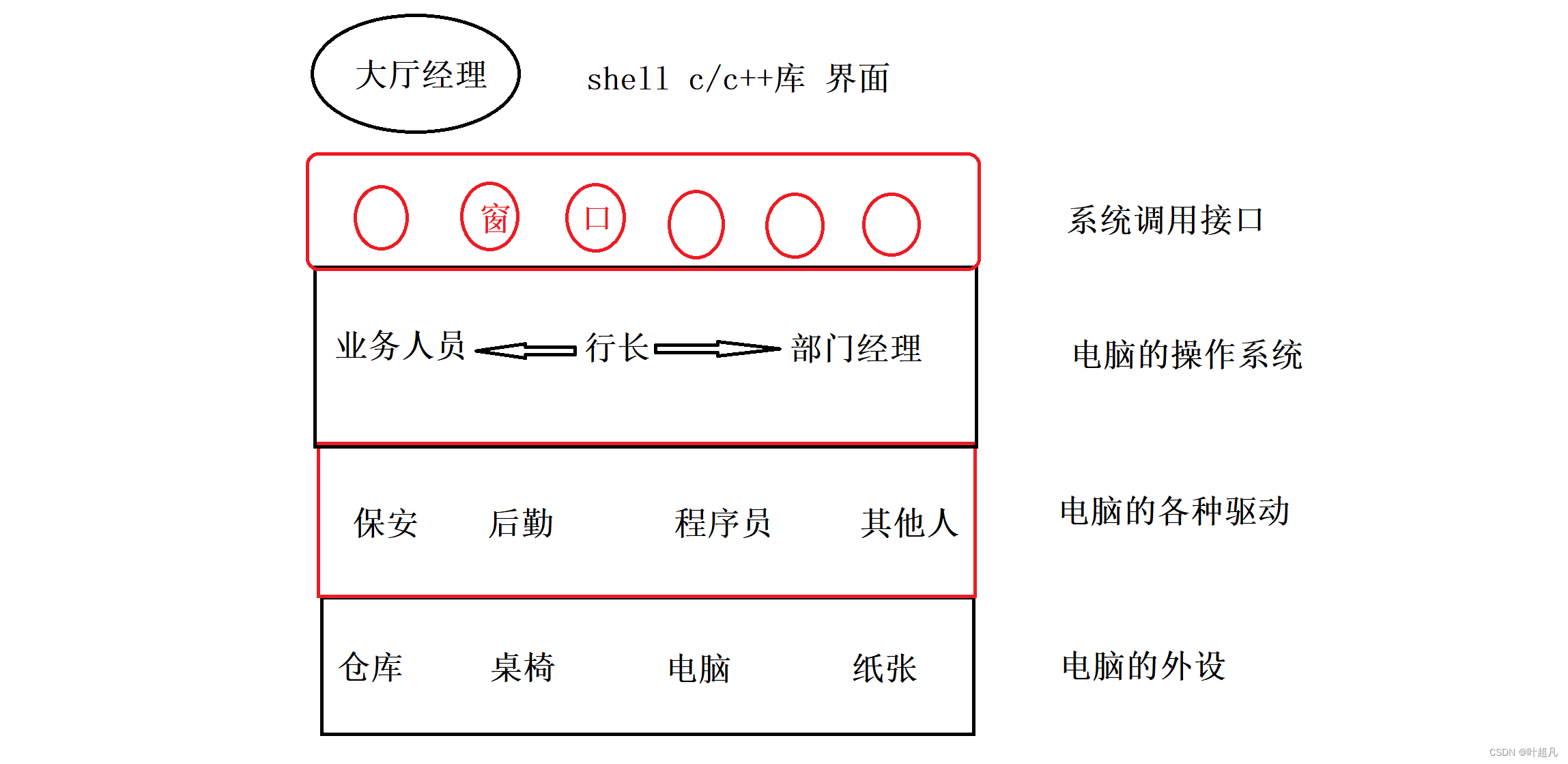
linux入门---操作体统的概念
什么是操作系统 操作系统是一个对软硬件资源进行管理的软件。计算机由一堆硬件组成,这些硬件遵循着冯诺依曼体系结构 在这个硬件的基础上还有一个软件叫做操作系统 操作系统的任务是对硬件进行管理,既然是管理的话操作系统得访问到底层的硬件…...
《Qt 6 C++开发指南》提供4个版本的示例程序
《Qt 6 C开发指南》包含丰富的示例项目,为了方便读者使用《Qt 6 C开发指南》学习Qt编程,本书提供了4个版本的示例程序。读者可在人民邮电出版社异步社区本书的配套资源(如图1)里下载这4个版本的示例程序。图1 异步社区本书配套资源…...

chartgpt 告诉我的,loss 函数的各种知识
一、libtorch中常见的损失函数及其使用场景的总结1. CrossEntropyLoss:CrossEntropyLoss(交叉熵损失)主要用于分类任务。它适用于多分类问题,其中每个样本只属于一个类别(互斥)。该损失函数将预测概率与真实标签的one-…...
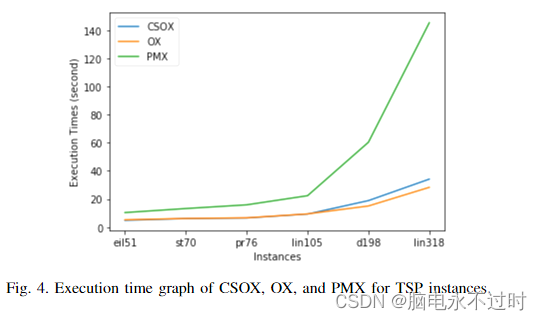
旅行推销员问题的遗传算法中的完整子路线顺序交叉
摘要 旅行商问题(TSP)是许多著名的组合问题之一。TSP可以解释为很难找到从第一个城市出发,经过所有城市,然后返回起点的最短距离。在标准问题中,TSP通常用于确定新算法的效率。遗传算法是求解TSP问题的一种成功算法。…...

Python实现词频统计
词频统计是自然语言处理的基本任务,针对一段句子、一篇文章或一组文章,统计文章中每个单词出现的次数,在此基础上发现文章的主题词、热词。 1. 单句的词频统计 思路:首先定义一个空字典my_dict,然后遍历文章…...
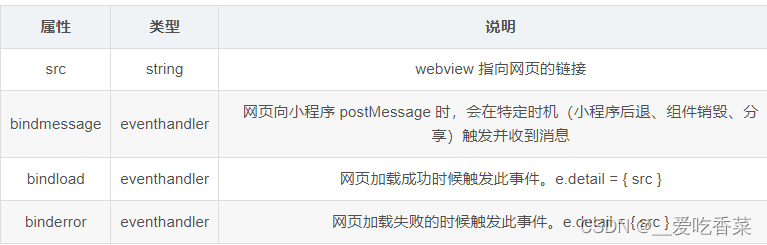
微信小程序面试题(day08)
文章目录微信小程序自定义组件的使用?微信小程序事件通道的使用?微信小程序如何使用vant组件库?微信小程序自定义组件父传子子传父?微信小程序自定义组件生命周期有哪些?微信小程序授权登录流程?web-view。…...
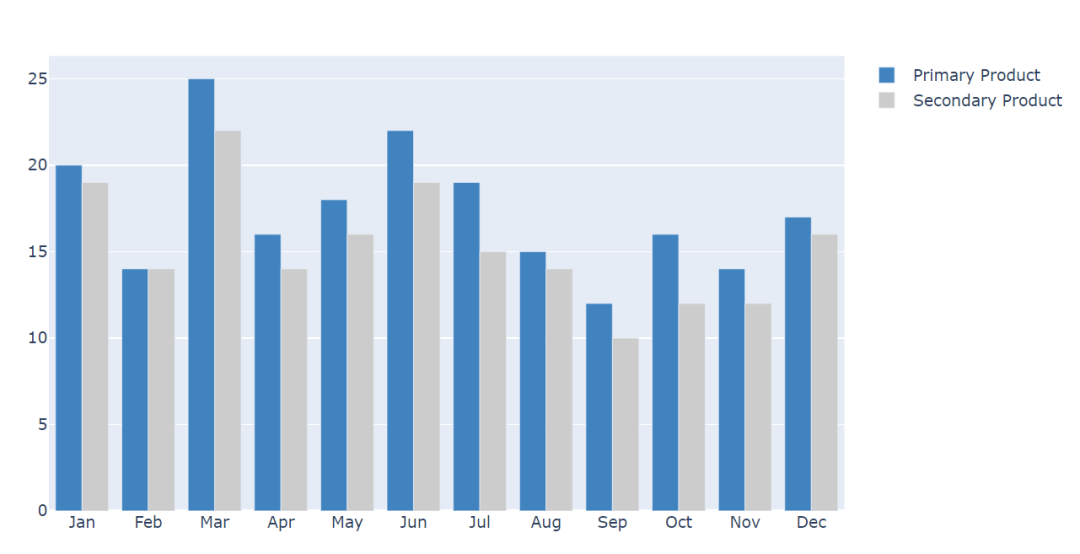
最强的Python可视化神器,你有用过么?
数据分析离不开数据可视化,我们最常用的就是Pandas,Matplotlib,Pyecharts当然还有Tableau,看到一篇文章介绍Plotly制图后我也跃跃欲试,查看了相关资料开始尝试用它制图。 1、Plotly Plotly是一款用来做数据分析和可视…...
Ubuntu使用vnc远程桌面【远程内网穿透】
文章目录1.前言2.两台互联电脑的设置2.1 Windows安装VNC2.2 Ubuntu安装VNC2.3.Ubuntu安装cpolar3.Cpolar设置3.1 Cpolar云端设置3.2.Cpolar本地设置4.公网访问测试5.结语1.前言 记得笔者刚刚开始接触电脑时,还是win95/98的时代,那时的电脑桌面刚迈入图形…...

【C++】map、set、multimap、multiset的介绍和使用
我讨厌世俗,也耐得住孤独。 文章目录一、键值对二、树形结构的关联式容器1.set1.1 set的介绍1.2 set的使用1.3 multiset的使用2.map2.1 map的介绍2.2 map的使用2.3 multimap的使用三、两道OJ题1.前K个高频单词(less<T>小于号是小的在左面升序&…...
)
css学习14(多媒体查询)
目录 多媒体查询 语法 示例代码 通用媒体查询 媒体功能参考列表 多媒体查询 CSS的媒体查询是一种CSS的技术,它可以根据不同的设备类型、屏幕尺寸、方向、分辨率等条件来应用不同的CSS样式,从而为不同的设备和屏幕提供最佳的浏览体验。这样ÿ…...
【C++进阶】C++11(中)左值引用和右值引用
文章目录左值引用左值引用的概念左值引用的使用右值引用右值引用的概念右值引用的使用左右值相互引用左值引用对右值进行引用右值引用对左值进行引用右值引用使用场景和意义左值引用的优势左值引用的短板右值引用的优势完美转发模板万能引用完美转发实际运用场景左值引用 左值…...

Python中的生成器【generator】总结,看看你掌握了没?
人生苦短,我用python python 安装包资料:点击此处跳转文末名片获取 1.实现generator的两种方式 python中的generator保存的是算法, 真正需要计算出值的时候才会去往下计算出值。 它是一种惰性计算(lazy evaluation)。 要创建一个…...
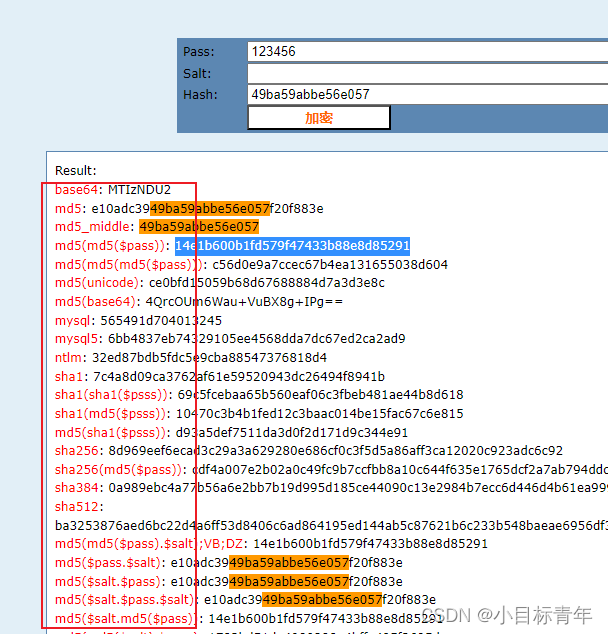
MD5加密竟然不安全,应届生表示无法理解?
前言 近日公司的一个应届生问我,他做的一个毕业设计密码是MD5加密存储的,为什么密码我帮他调试的时候,我能猜出来明文是什么? 第六感,是后端研发的第六感! 正文 示例,有个系统,前…...
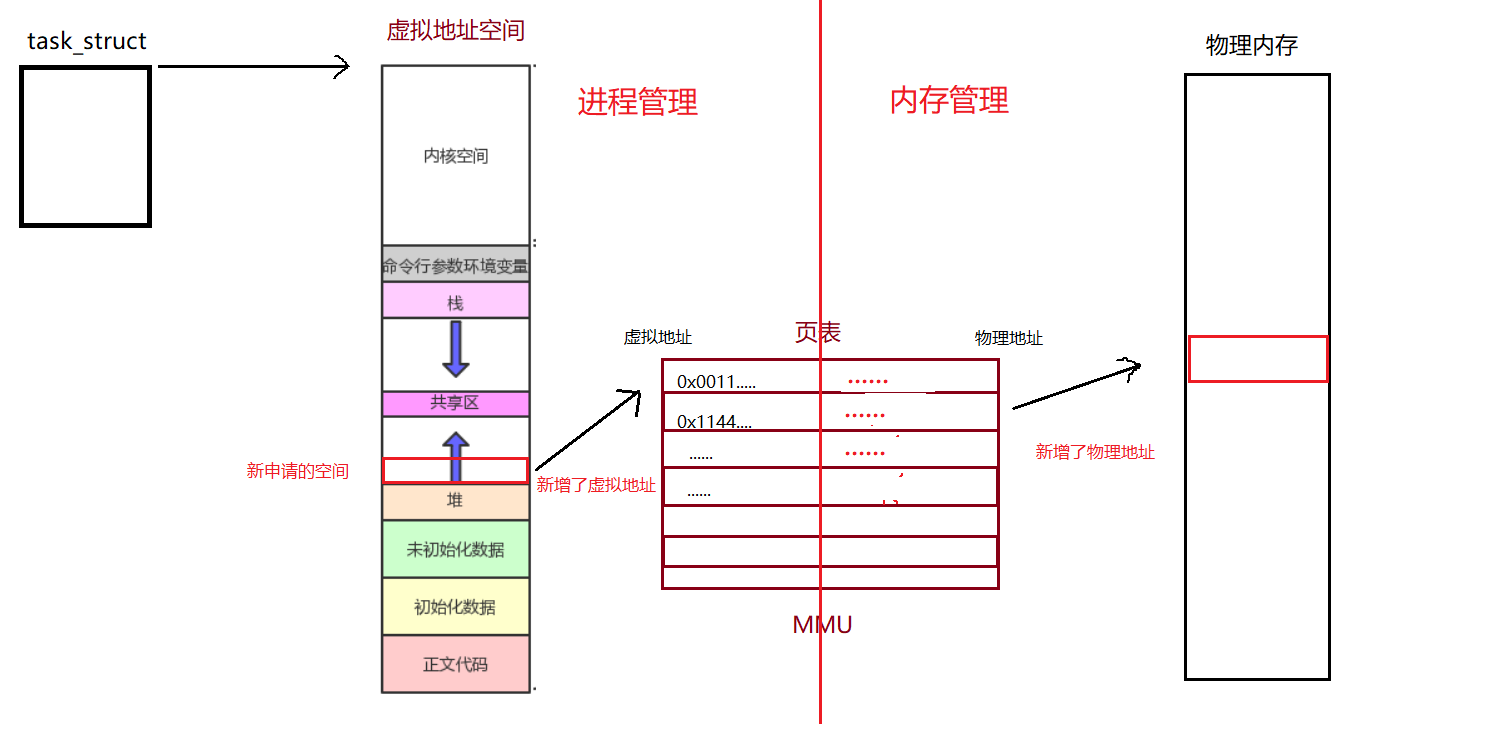
【Linux】虚拟地址空间
进程地址空间一、引入二、虚拟地址与物理内存的联系三、为什么要有虚拟地址空间一、引入 对于C/C程序,我们眼中的内存是这样的: 我们利用这种对于与内存的理解看一下下面这段代码: 运行结果: 观察父子进程中 val 变量的值&…...
四平方和题解(二分习题)
四平方和 暴力做法 Y总暴力做法,蓝桥云里能通过所有数据 总结:暴力也分好坏,下面这份代码就是写的好的暴力 如何写好暴力:1. 按组合枚举 2. 写好循环结束条件,没必要循环那么多次 #include<iostream> #include<cmath>…...

一篇文章搞定js正则表达式
我们测试正则表达式是否正确的方法有很多,例如通过正则表达式找到拼配的字符串: 在vscode编辑器中点击搜索框中的第三个按钮就可以实现: 或者 在浏览器中的控制台也可以实现: 我们可以通过下面的在线网站来测试你写的正则是否正确…...
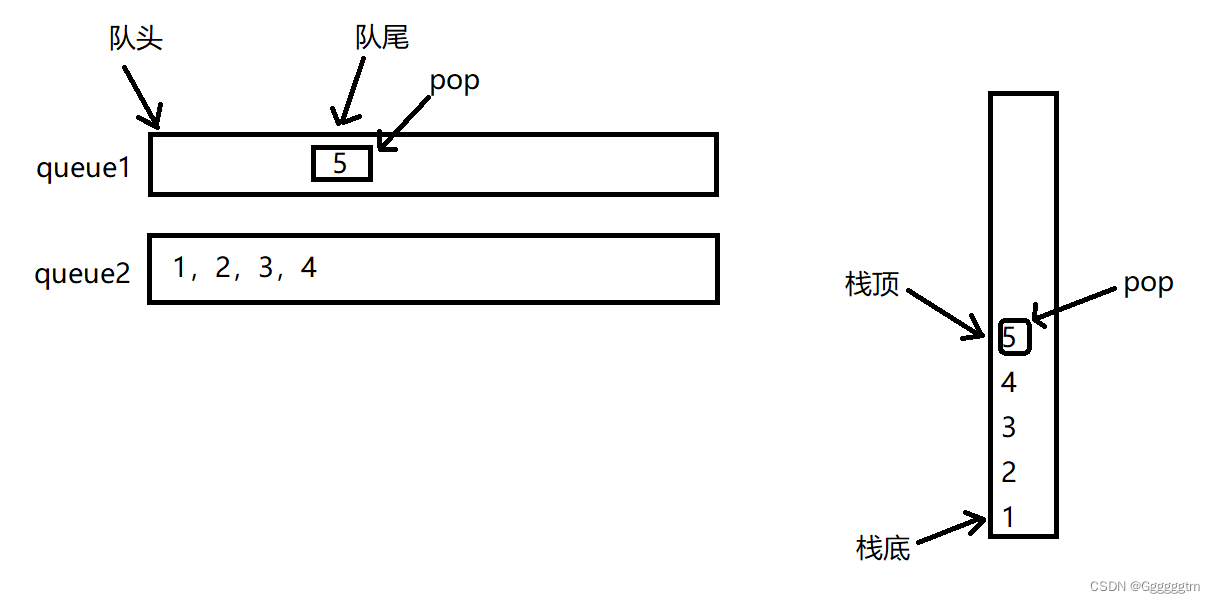
[数据结构] 用两个队列实现栈详解
文章目录 一、队列实现栈的特点分析 1、1 具体分析 1、2 整体概括 二、队列模拟实现栈代码的实现 2、1 手撕 队列 代码 queue.h queue.c 2、2 用队列模拟实现栈代码 三、总结 🙋♂️ 作者:Ggggggtm 🙋♂️ 👀 专栏࿱…...

官宣|Apache Flink 1.17 发布公告
Apache Flink PMC(项目管理委员)很高兴地宣布发布 Apache Flink 1.17.0。Apache Flink 是领先的流处理标准,流批统一的数据处理概念在越来越多的公司中得到认可。得益于我们出色的社区和优秀的贡献者,Apache Flink 在 Apache 社区…...
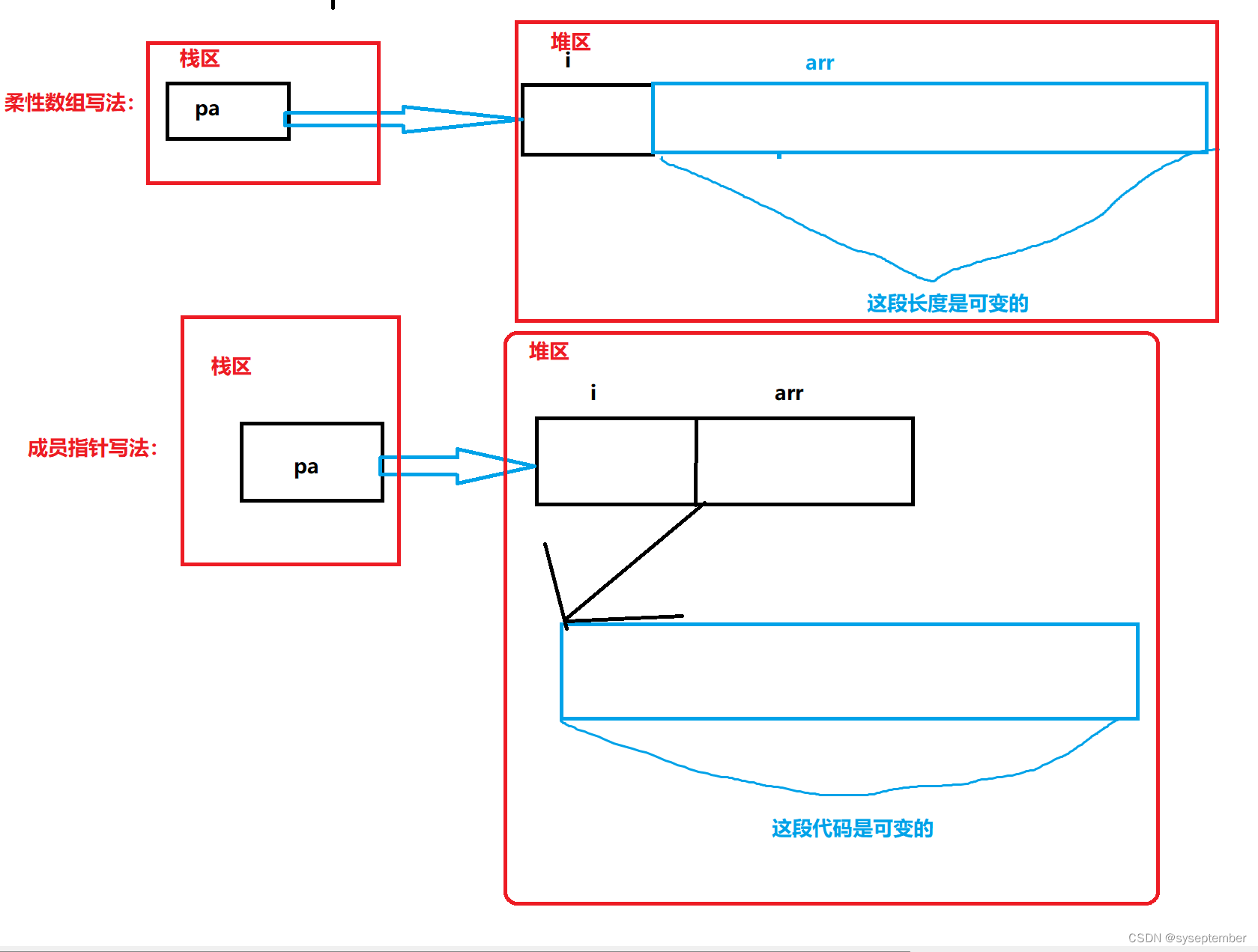
动态内存管理+动态通讯录【C进阶】
文章目录为什么存在动态内存分配❓👉动态内存函数👈malloc&freecallocrealloc❌常见的动态内存错误❌练习题🫠C/C程序的内存开辟🤔柔性数组柔性数组的特点柔性数组的优势:star:动态通讯录:star:初始化添加销毁为什么存在动态内…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...
