【Py/Java/C++三种语言详解】LeetCode743、网络延迟时间【单源最短路问题Djikstra算法】
可上 欧弟OJ系统 练习华子OD、大厂真题
绿色聊天软件戳od1441了解算法冲刺训练(备注【CSDN】否则不通过)
文章目录
- 相关推荐阅读
- 一、题目描述
- 二、题目解析
- 三、参考代码
- Python
- Java
- C++
- 时空复杂度
- 华为OD算法/大厂面试高频题算法练习冲刺训练
相关推荐阅读
- Dijkstra算法的具体介绍详见单源最短路问题:Dijkstra算法详解【经典算法,限时免费】)
一、题目描述
题目链接:https://leetcode.cn/problems/network-delay-time/description/
有 n 个网络节点,标记为 1 到 n。
给你一个列表 times,表示信号经过 有向 边的传递时间。 times[i] = (u(i), v(i), w(i)),其中 u(i) 是源节点,v(i) 是目标节点, w(i) 是一个信号从源节点传递到目标节点的时间。
现在,从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号?如果不能使所有节点收到信号,返回 -1 。
示例 1:
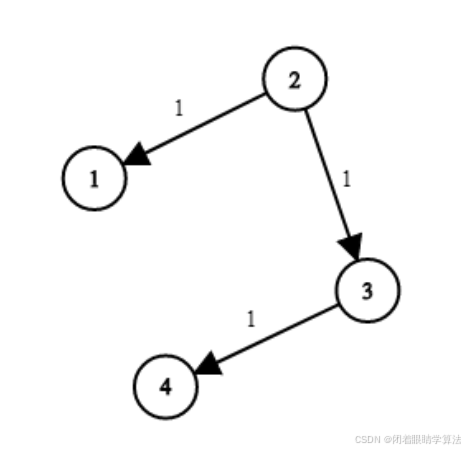
输入:times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
输出:2
示例 2:
输入:times = [[1,2,1]], n = 2, k = 1
输出:1
示例 3:
输入:times = [[1,2,1]], n = 2, k = 2
输出:-1
提示:
1 <= k <= n <= 1001 <= times.length <= 6000times[i].length == 31 <= u(i), v(i) <= nu(i) != v(i)0 <= w(i) <= 100- 所有
(u(i), v(i))对都 互不相同(即,不含重复边)
二、题目解析
题目要求计算从源点出发到达所有其他节点的最短路径,在所有最短路径中找到最大值。
所以这是一个单源最短路问题,可以使用Dijkstra算法来解决,计算出dist数组之后取最大值即可。
Dijkstra算法的具体介绍详见单源最短路问题:Dijkstra算法详解【经典算法,限时免费】)
三、参考代码
Python
INF = 100000 # 用于表示一个非常大的数,作为初始的最短距离class Solution:def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:# 创建一个邻接表,用于存储每个节点的相邻节点及对应的路径权重neighbor_dic = defaultdict(list)for a, b, w in times:# 将边 (a -> b) 和对应的权重 w 加入邻接表neighbor_dic[a].append((b, w)) # 初始化一个列表 dist,用于记录从源节点 k 到每个节点的最短距离# 初始时,所有节点的距离都设置为 INF(表示尚未访问或不可达)dist = [INF] * (n+1)# 初始化一个最小堆,用于在Dijkstra算法中提取当前已知最短路径的节点# 堆中元素是 (当前时间, 当前节点) 元组heap = [(0, k)]# 进行Dijkstra(类似BFS)while heap:# 从堆中弹出当前时间最小的节点cur_time, cur_node = heappop(heap)# 如果当前节点的已记录最短时间比当前时间更小,说明已经找到更优的路径# 因此可以跳过当前节点if cur_time > dist[cur_node]:continue# 更新从源节点 k 到当前节点的最短时间dist[cur_node] = cur_time# 遍历当前节点的所有相邻节点for next_node, next_weight in neighbor_dic[cur_node]:# 计算通过当前节点到达相邻节点所需的时间next_time = cur_time + next_weight# 如果通过当前节点到达相邻节点的时间比之前记录的最短时间更短# 则更新相邻节点的最短时间,并将其加入堆中以便进一步探索if next_time < dist[next_node]:heappush(heap, (next_time, next_node))# 找到从源节点 k 到所有节点的最短路径中的最大值ans = max(dist[1:])# 如果最大值小于 INF,说明所有节点都可达,返回最大值作为网络延迟时间# 否则返回 -1,表示有节点无法到达return ans if ans < INF else -1
Java
import java.util.*;class Solution {static final int INF = 100000; // 用于表示一个非常大的数,作为初始的最短距离public int networkDelayTime(int[][] times, int n, int k) {// 创建一个邻接表,用于存储每个节点的相邻节点及对应的路径权重Map<Integer, List<int[]>> neighbor_dic = new HashMap<>();for (int i = 1; i <= n; i++) {neighbor_dic.put(i, new ArrayList<>());}for (int[] time : times) {int a = time[0], b = time[1], w = time[2];// 将边 (a -> b) 和对应的权重 w 加入邻接表neighbor_dic.get(a).add(new int[]{b, w});}// 初始化一个数组 dist,用于记录从源节点 k 到每个节点的最短距离// 初始时,所有节点的距离都设置为 INF(表示尚未访问或不可达)int[] dist = new int[n + 1];Arrays.fill(dist, INF);dist[k] = 0; // 源节点到自己的距离为0// 初始化一个最小堆,用于在Dijkstra算法中提取当前已知最短路径的节点// 堆中元素是 (当前时间, 当前节点) 元组PriorityQueue<int[]> heap = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));heap.offer(new int[]{0, k});// 进行Dijkstra(类似BFS)while (!heap.isEmpty()) {// 从堆中弹出当前时间最小的节点int[] cur = heap.poll();int cur_time = cur[0], cur_node = cur[1];// 如果当前节点的已记录最短时间比当前时间更小,说明已经找到更优的路径// 因此可以跳过当前节点if (cur_time > dist[cur_node]) {continue;}// 遍历当前节点的所有相邻节点for (int[] neighbor : neighbor_dic.getOrDefault(cur_node, new ArrayList<>())) {int next_node = neighbor[0], next_weight = neighbor[1];// 计算通过当前节点到达相邻节点所需的时间int next_time = cur_time + next_weight;// 如果通过当前节点到达相邻节点的时间比之前记录的最短时间更短// 则更新相邻节点的最短时间,并将其加入堆中以便进一步探索if (next_time < dist[next_node]) {dist[next_node] = next_time;heap.offer(new int[]{next_time, next_node});}}}// 找到从源节点 k 到所有节点的最短路径中的最大值int ans = Arrays.stream(dist).skip(1).max().getAsInt();// 如果最大值小于 INF,说明所有节点都可达,返回最大值作为网络延迟时间// 否则返回 -1,表示有节点无法到达return ans < INF ? ans : -1;}
}
C++
int INF = 100000; // 用于表示一个非常大的数,作为初始的最短距离class Solution {
public:int networkDelayTime(vector<vector<int>>& times, int n, int k) {// 创建一个邻接表,用于存储每个节点的相邻节点及对应的路径权重unordered_map<int, vector<pair<int, int>>> neighbor_dic;for (const auto& time : times) {int a = time[0], b = time[1], w = time[2];// 将边 (a -> b) 和对应的权重 w 加入邻接表neighbor_dic[a].push_back({b, w});}// 初始化一个列表 dist,用于记录从源节点 k 到每个节点的最短距离// 初始时,所有节点的距离都设置为 INF(表示尚未访问或不可达)vector<int> dist(n + 1, INF);dist[k] = 0; // 起点距离为0// 初始化一个最小堆,用于在Dijkstra算法中提取当前已知最短路径的节点// 堆中元素是 (当前时间, 当前节点) 元组priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> heap;heap.push({0, k});// 进行Dijkstra算法(类似BFS)while (!heap.empty()) {// 从堆中弹出当前时间最小的节点auto [cur_time, cur_node] = heap.top();heap.pop();// 如果当前节点的已记录最短时间比当前时间更小,说明已经找到更优的路径// 因此可以跳过当前节点if (cur_time > dist[cur_node]) {continue;}// 遍历当前节点的所有相邻节点for (auto& [next_node, next_weight] : neighbor_dic[cur_node]) {// 计算通过当前节点到达相邻节点所需的时间int next_time = cur_time + next_weight;// 如果通过当前节点到达相邻节点的时间比之前记录的最短时间更短// 则更新相邻节点的最短时间,并将其加入堆中以便进一步探索if (next_time < dist[next_node]) {dist[next_node] = next_time;heap.push({next_time, next_node});}}}// 找到从源节点 k 到所有节点的最短路径中的最大值int ans = *max_element(dist.begin() + 1, dist.end());// 如果最大值小于 INF,说明所有节点都可达,返回最大值作为网络延迟时间// 否则返回 -1,表示有节点无法到达return ans < INF ? ans : -1;}
};
时空复杂度
时间复杂度:O((V+E)logV)。
空间复杂度:O(V+E)。
其中V是节点数,E是边数。
华为OD算法/大厂面试高频题算法练习冲刺训练
-
华为OD算法/大厂面试高频题算法冲刺训练目前开始常态化报名!目前已服务300+同学成功上岸!
-
课程讲师为全网50w+粉丝编程博主@吴师兄学算法 以及小红书头部编程博主@闭着眼睛学数理化
-
每期人数维持在20人内,保证能够最大限度地满足到每一个同学的需求,达到和1v1同样的学习效果!
-
60+天陪伴式学习,40+直播课时,300+动画图解视频,300+LeetCode经典题,200+华为OD真题/大厂真题,还有简历修改、模拟面试、专属HR对接将为你解锁
-
可上全网独家的欧弟OJ系统练习华子OD、大厂真题
-
可查看链接 大厂真题汇总 & OD真题汇总(持续更新)
-
绿色聊天软件戳
od1336了解更多
相关文章:

【Py/Java/C++三种语言详解】LeetCode743、网络延迟时间【单源最短路问题Djikstra算法】
可上 欧弟OJ系统 练习华子OD、大厂真题 绿色聊天软件戳 od1441了解算法冲刺训练(备注【CSDN】否则不通过) 文章目录 相关推荐阅读一、题目描述二、题目解析三、参考代码PythonJavaC 时空复杂度 华为OD算法/大厂面试高频题算法练习冲刺训练 相关推荐阅读 …...

交替输出
交替输出 题目:线程 1 输出 a 5 次,线程 2 输出 b 5 次,线程 3 输出 c 5 次。现在要求输出 abcabcabcabcabc wait notify 版 public class SyncWaitNotify {private volatile int flag;private volatile int loopNumber;public SyncWaitNo…...
——更改html内数据)
JS(三)——更改html内数据
获取 DOM 元素,然后修改其属性或内容。使用 getElementById 方法获取特定 ID 的元素: <p id"myParagraph">这是初始的文本</p> const paragraph document.getElementById(myParagraph); paragraph.innerHTML 这是修改后的文本…...

CSS小玩意儿:文字适配背景
一,效果 二,代码 1,搭个框架 添加一张背景图片,在图片中显示一行文字。 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" conte…...
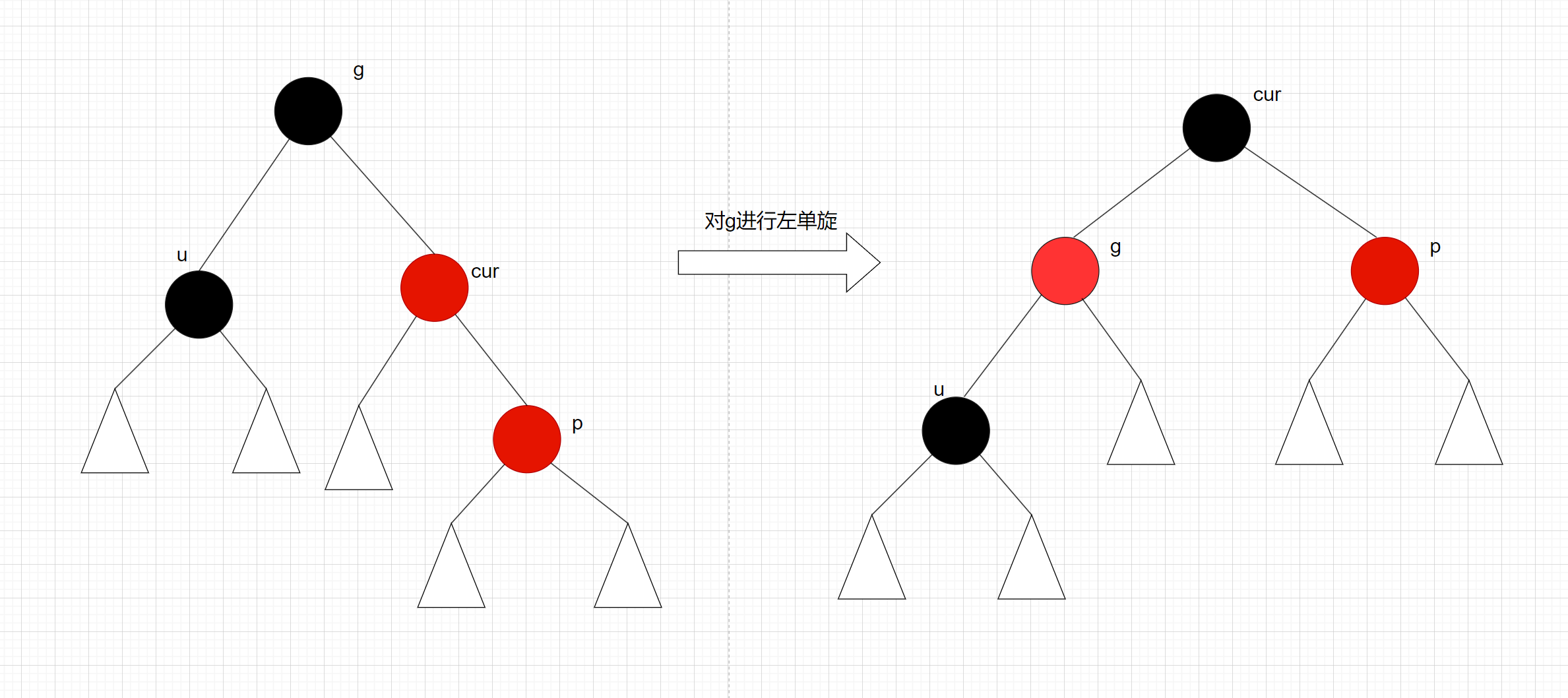
C++:平衡二叉搜索树之红黑树
一、红黑树的概念 红黑树, 和AVL都是二叉搜索树, 红黑树通过在每个节点上增加一个储存位表示节点的颜色, 可以是RED或者BLACK, 通过任何一条从根到叶子的路径上各个节点着色方式的限制,红黑树能够确保没有一条路径会比…...

CentOS 7 系统优化
CentOS 7 系统优化 1、配置YUM源 阿里云的YUM源配置: CentOS 7使用以下命令: sudo wget -O /etc/yum.repos.d/CentOS-Base.repo http://mirrors.aliyun.com/repo/Centos-7.repoCentOS 8使用以下命令: sudo wget -O /etc/yum.repos.d/CentOS…...

扫雷游戏——附源代码
扫雷游戏的源代码比较简单,不设计比较复杂的代码,主要是多个函数的组合,每个函数执行自己的功能,最终支持游戏的完成。 1.菜单 我们需要一个提醒信息来让用户进行选择。 void menu() {printf("***********************\n&…...
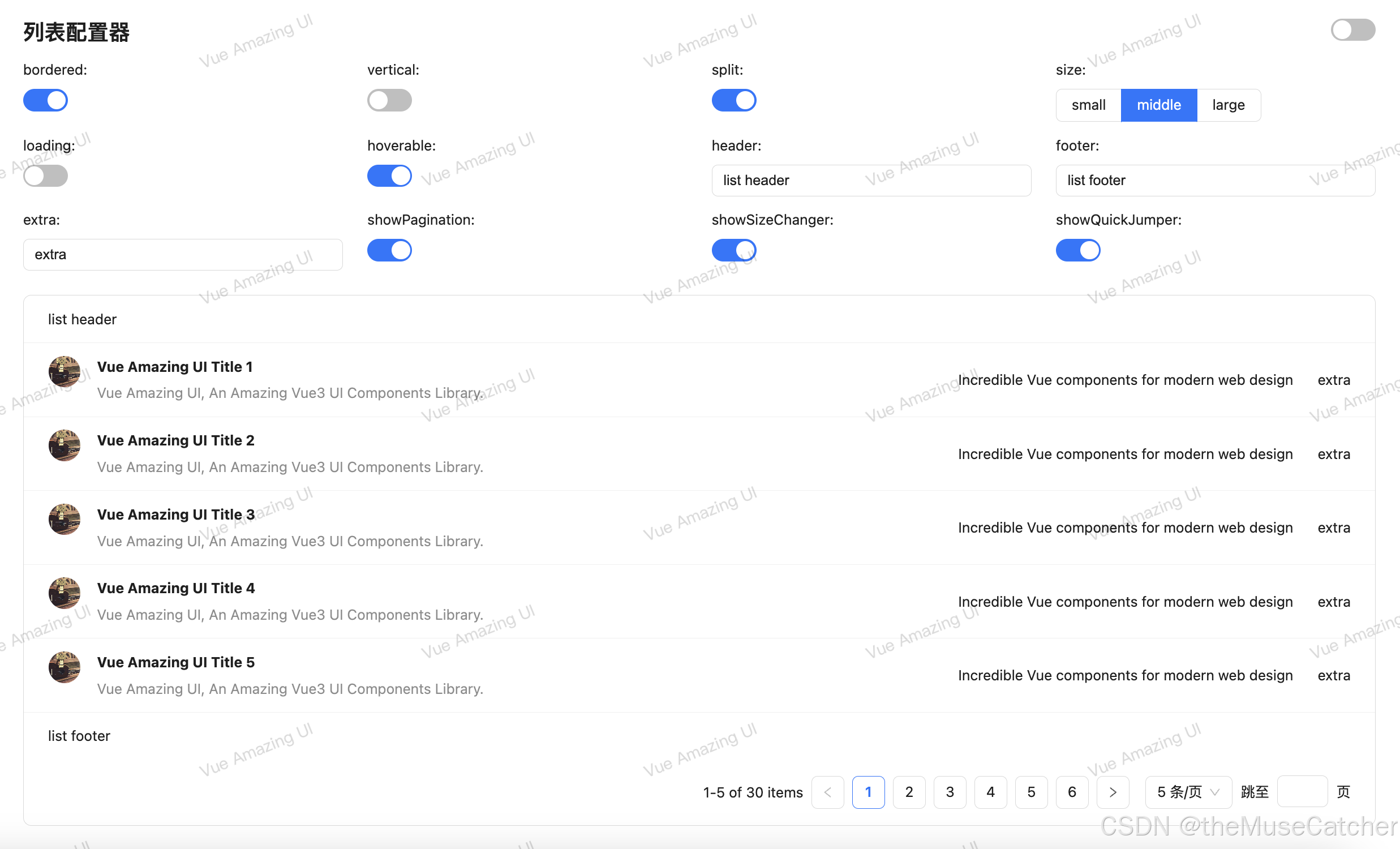
Vue3列表(List)
效果如下图:在线预览 APIs List 参数说明类型默认值bordered是否展示边框booleanfalsevertical是否使用竖直样式booleanfalsesplit是否展示分割线booleantruesize列表尺寸‘small’ | ‘middle’ | ‘large’‘middle’loading是否加载中booleanfalsehoverable是否…...

HarmonyOS NEXT - Navigation组件封装BaseNavigation
demo 地址: https://github.com/iotjin/JhHarmonyDemo 代码不定时更新,请前往github查看最新代码 在demo中这些组件和工具类都通过module实现了,具体可以参考HarmonyOS NEXT - 通过 module 模块化引用公共组件和utils 官方介绍 组件导航 (Navigation)(推…...
浅看MySQL数据库
有这么一句话:“一个不会数据库的程序员不是合格的程序员”。有点夸张,但是确是如此。透彻学习数据库是要学习好多知识,需要学的东西也是偏难的。我们今天来看数据库MySQL的一些简单基础东西,跟着小编一起来看一下吧。 什么是数据…...
)
Pytorch常用训练套路框架(CPU)
文章目录 1. 数据准备示例:加载 CIFAR-10 数据集 2. 模型定义示例:定义一个简单的卷积神经网络 3. 损失函数和优化器示例:定义损失函数和优化器 4. 训练循环示例:训练循环 5. 评估和测试示例:评估模型 6. 保存和加载模…...

C++ | Leetcode C++题解之第338题比特位计数
题目: 题解: class Solution { public:vector<int> countBits(int n) {vector<int> bits(n 1);for (int i 1; i < n; i) {bits[i] bits[i & (i - 1)] 1;}return bits;} };...
智慧校园云平台电子班牌系统源码,智慧教育一体化云解决方案
智慧校园云平台电子班牌系统,利用先进的云计算技术,将教育信息化资源和教学管理系统进行有效整合,实现生态基础数据共享、应用生态统一管理,为智慧教育建设的统一性,稳定性,可扩展性,互通性提供…...

数据库系统 第17节 数据仓库 案例赏析
下面我将通过几个具体的案例来说明数据仓库如何在不同的行业中发挥作用,并解决实际业务问题。 案例 1: 零售业 背景: 一家大型零售商希望改进其库存管理和市场营销策略,以提高销售额和顾客满意度。 解决方案: 数据仓库: 构建一个数据仓库࿰…...
硬件面试经典 100 题(71~90 题)
71、请问下图电路的作用是什么? 该电路实现 IIC 信号的电平转换(3.3V 和 5V 电平转换),并且是双向通信的。 上下两路是一样的,只分析 SDA 一路: 1) 从左到右通信(SDA2 为输入状态&…...

【git】代理相关
问题: 开启了翻墙代理工具,拉取代码时报错:fatal: 无法访问 xxxx : Failed to connect to github.com port 443: 连接超时 解决: 0,取消代理仍然无法拉取 1,查看控制面板-网络与Internet-代理ÿ…...
方式和闭包函数方式定义gin中间件)
golang gin框架中创建自定义中间件的2种方式总结 - func(*gin.Context)方式和闭包函数方式定义gin中间件
在gin框架中,我们可以通过2种方式创建自定义中间件: 1. 直接定义一个类型为 func(*gin.Context)的函数或者方法 这种方式是我们常用的方式,也就是定义一个参数为*gin.Context的函数或者方法。定义的方法就是创建一个 参数类型为 gin.Handler…...

Linux高级编程 8.13 文件IO
一、文件IO 操作系统为了方便用户使用系统功能而对外提供的一组系统函数。称之为 系统调用(unistd.h) 其中有个 文件IO,一般都是对设备文件操作,当然也可以对普通文件进行操作。 这是一个基于Linux内核的没有缓存的IO机制 文件IO特性&…...

【k8s】ubuntu18.04 containerd 手动从1.7.15 换为1.7.20
ubutnu18.04之前手动安装了1.7.15现在下载1.7.20containerd-1.7.20-linux-amd64.tar.gz root@k8s-worker-i58265u:/home/zhangbin# root@k8s-worker-i58265u:/home/zhangbin# https://github.com/containerd/containerd/releases/download/v1.7.20/containerd-1.7.20-linux-am…...

常用浮动方式
目录 一、标准流 二、float浮动 三、 flex浮动 3.1flex组成 3.2 主轴对齐方式 3.3侧轴对齐方式 3.4修改主轴方向 3.5弹性盒子换行 3.6行对齐方式 一、标准流 标签在网页中的默认排布规则 例如: 块元素独占一行、行内元素可以一行显示多个 二、float浮动 让块…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...
